1. Ingeniería

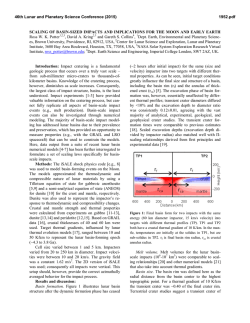
46th Lunar and Planetary Science Conference (2015)
2212.pdf
IMPACT BASIN FORMATION ON MARS: FROM BOREALIS TO THE LATE HEAVY
BOMBARDMENT. E. J. Davies1, S. T. Stewart1, R. J. Lillis2. 1Department of Earth and Planetary Sciences, U.
California, Davis, CA ([email protected]). 2Space Sciences Laboratory, U. California, Berkeley, CA.
Introduction: The Martian crust preserves the imprint of 20 large (>1000 km) impact basins [1] and a
global dichotomy that is hypothesized to have formed
via a planetary-scale impact event [2]. The impact basin record spans the cessation of the Martian dynamo
magnetic field [3], and the youngest impact basins
have the cleanest shock-demagnetization signatures
[4]. The youngest basins are also the least degraded
and have more pronounced crustal thinning within the
structure compared to older basins [5].
These observations imply a period of time between
the older basins and the 4 youngest impact basins. The
length of this interlude is unknown because the impactor flux is uncertain and uncalibrated for early Mars
(prior to ~3.9 Gyr ago). The fast formation time of
Mars (~44% formed in 2 Myr [6, 7]) and evidence for
early crust formation (prior to 4.428±0.035 Ga from
meteorite NWA 7533 [8, 9] and 4.21±0.35 Ga at Gale
crater [10]) allow for the possibility of a significant
difference in the thermal state of the planet between
creation of the oldest and youngest impact basins associated with the late heavy bombardment (~3.9 Ga). The
crustal dichotomy itself is an ancient feature and the
northern lowlands and southern highlands have a similar number density of impact basins [11].
Here, we consider the mechanics of impact basin
formation under a range of crustal thickness and thermal gradients on Mars. The final size of an impact
basin is sensitive to the thermal gradient [12]. The observed radial extent of crustal thinning and demagnetization can help deconvolve the ambiguities between
the impact energy and initial thermal state. This work
will help constrain the possible impact energies and
impactor sizes that produced the observed basins. For
Borealis-scale events, this work improves the initial
conditions for subsequent mantle convection and crust
formation models.
Numerical Method. Basin formation is modeled
using the CTH shock physics code [13] with a fixed
central gravity field in 2D and self-gravity in 3D. Mars
is initialized in gravitational equilibrium with varying
thermal profiles. Multiphase model equations of state
are used for iron [14], forsterite [15], and silica [16].
The pressure, temperature, and strain-rate dependent
rheological model includes a brittle regime for the
crust and uppermost mantle [17, 18] and a creep regime for the deeper mantle [19]. The peridotite solidus
and olivine liquidus are used to calculate melting [20].
Crater collapse involves a two-phase flow of melt and
solid clasts. This complex debris flow is modeled using
a simplified approach: when the temperature exceeds
the solidus, (i) a pressure-dependent friction law (coefficient of 0.1–0.2 based on melt-lubricated faults [21])
is used at high strain rates (>10-4 s-1) and (ii) a Newtonian fluid rheology is used at low strain rates (when
the viscosity of the fluid dominates [22]). Model parameters are constrained by laboratory data.
The Borealis Impact Hypothesis: Figure 1 presents an example calculation of the impact hypothesis
for formation of a global crustal dichotomy. The impact conditions correspond to the “sweet spot” found
in [23] that excavates the outer layers of the planet
over an area similar to the northern lowlands without
significant disruption of the antipode hemisphere.
Previous numerical models of a Borealis-scale impact utilized a Smoothed Particle Hydrodynamics code
that did not include the crust or a rock rheology model
(purely hydrodynamic) [23, 24]. The dynamics of large
impact crater formation are dominated by gravitational
forces, so the transient crater size is very similar with
and without material strength.
However, some important differences arise from
the inclusion of a strength model. The global planetary
oscillations observed in the hydrodynamic case (10’s
to 100’s km in amplitude [24] are absent (or significantly muted) with strength. A similar result was found
in the planetary-scale impact study by [25] when
strength was included.
Heating of the mantle is significantly higher in the
impacted hemisphere when strength is included (Figure 1). Heating (from shock and shear deformation) is
more localized with strength. The work done by shear
deformation during transient crater formation and collapse raises the temperature of the deep mantle in the
impacted hemisphere to the solidus; the generation of
partial melt reduces the effective strength of the material and localizes heating at late times during the impact event. The amount of melt generated in the impacted hemisphere is significantly higher compared to
estimates from hydrodynamic calculations [25]. The
example calculation in Figure 1 begins with a cold
initial Mars and the sensitivity of melt production on
the initial thermal gradient will be presented.
Discussion: Our simulations with material strength
provide new information about the viability of the impact formation hypothesis for the global crustal dichotomy. Because subsequent crust production in the impacted hemisphere may exceed the crustal thickness of
the antipode region, an exogenic-endogenic variation
of the impact hypothesis has been proposed [26-29]. In
46th Lunar and Planetary Science Conference (2015)
these ‘South Pole Impact’ models, the impact leads to
generation of the thicker crust in the southern highlands. Both northern and southern impact models for
the dichotomy require specific conditions for the evolution of the dynamo to explain the concentration of
highly magnetized crust in the highlands.
The initial conditions for the subsequent crust production have assumed a spherical/hemispherical zone
of heating or spherical iron core near the surface of the
impacted hemisphere. Our calculations show that the
zone of heating is not hemispherical when shear deformation and crater collapse are included. In addition,
the impactor core is sheared and dispersed around the
planet with only a portion lining the impact melt in the
collapsed basin. The size distribution of the dispersed
core fragments is uncertain. Thus, it is difficult to ascertain how much material may be large enough to
descend through the crust and mantle as diapirs and
how much may remain mixed into the antipode crust.
Scaling Laws for Impact Basin Formation: We
will present the relationships between impact energy
and final basin size for different initial thermal gradients and crustal thicknesses. We will also consider the
sensitivity of the basin scaling law to the material parameters used in the rock rheology model. Using the
additional constraints of observed crustal thickness and
radius of demagnetization, we shall further constrain
the impact energies for the youngest impact basins.
2212.pdf
Acknowledgements: This work was supported by
NASA grants NNX11AE96G and NNX11AI85G.
References: [1] Frey, H. (2008) GRL 35, L13203. [2]
Wilhelms, D.E. and S.W. Squyres (1984) Nature 309, 138.
[3] Lillis, R.J., et al. (2008) GRL 35, L14203. [4] Acuña, M.,
et al. (1999) Science 284, 790. [5] Minton, D., et al. (2012)
Early Solar System Impact Bombardment II, 4040. [6] Tang,
H. and N. Dauphas (2014) EPSL 390, 264. [7] Dauphas, N.
and A. Pourmand (2011) Nature 473, 489. [8] Humayun, M.,
et al. (2013) Nature 503, 513. [9] Bellucci, J., et al. (2015)
EPSL 410, 34. [10] Farley, K., et al. (2014) Science 343,
1247166. [11] Frey, H.V., et al. (2002) GRL 29, 1384. [12]
Miljković, K., et al. (2013) Science 342, 724. [13] McGlaun,
J.M., et al. (1990) Int. J. Impact Eng. 10, 351. [14] Kerley,
G.I. (1993), Report SAND93-0027, Sandia National
Laboratory. [15] Canup, R.M. (2012) Science 338, 1052. [16]
Melosh, H.J. (2007) MAPS 42, 2079. [17] Senft, L.E. and
S.T. Stewart (2009) EPSL 287, 471. [18] Zucker, R.V. and
S.T. Stewart (2010) LPSC 41, 2722. [19] Kawazoe, T., et al.
(2009) PEPI 174, 128. [20] Zhang, J. and C. Herzberg
(1994) JGR 99, 17729. [21] Del Gaudio, P., et al. (2009)
JGR 114, B06306. [22] Kohlstedt, D.L. (2002) Rev. Min.
Geochem. 51, 121. [23] Marinova, M.M., et al. (2008)
Nature 453, 1216. [24] Marinova, M.M., et al. (2011) Icarus
211, 960. [25] Leinhardt, Z.M., et al. (2010) ApJ 714, 1789.
[26] Reese, C., et al. (2010) JGR 115, E05004. [27] Reese,
C., et al. (2011) Icarus 213, 433. [28] Golabek, G.J., et al.
(2011) Icarus 215, 346. [29] Leone, G., et al. (2014) GRL 41,
10.1002/2014GL062261. [30] Wieczorek, M.A., et al. (2012)
Science 335, 1212. [31] Stewart, S.T. (2011) LPSC 42,
1633.
Figure 1. Simulation of a Borealis-scale impact event [similar to Fig. 2D in 23] using the CTH shock physics code with the rock
rheology model from [30, 31]. View of the plane through the center of planet with colors denoting material (upper row) and temperature (lower row). Example 3×1029 J event: a 2200 km differentiated projectile (dark grey core and brown mantle) hits Mars
(light grey core; grey mantle; blue 60 km thick surface layer of crust) at 6 km/s and 45°. With a rock rheology model, the mantle
heating is localized to the impact hemisphere. The entire surface is heated by secondary impacts, including fragments of the core
of a differentiated impactor. Note that the calculated temperatures do not include the latent heat of melting (due to incomplete
equations of state but it is approximated in the rheology model); partial and complete melt correspond to dark red and black.