1. Ingeniería

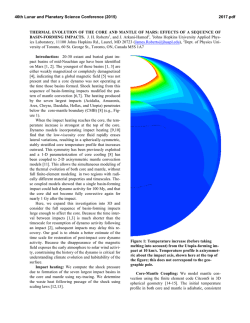
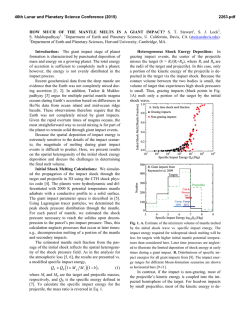
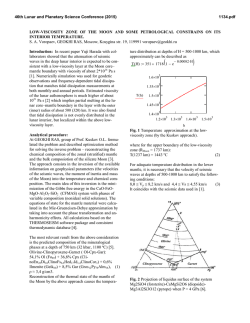
46th Lunar and Planetary Science Conference (2015)
2900.pdf
Mars Thermal History: Core, Atmosphere, Mantle, Phobos, and Surface (MaTH CAMPS). M. S. Duncan1, M.
B. Weller1, J. K. Wicks2, N. R. Knezek3, B. A. Black3, S. A. Johnston4, S. Hongsresawat5, N. J. Towles6, C. Thissen7, N. C. Schmerr4, M. P. Panning5, L. Montési4, M. Manga3 and P. Lognonné8; 1Rice Univ., Houston, TX, USA;
2
Princeton Univ., Princeton, NJ, USA; 3Univ. of California, Berkeley, CA, USA; 4Univ. of Maryland College Park,
College Park, MD, USA; 5Univ. of Florida, Gainesville, FL, USA; 6Johns Hopkins Univ., Baltimore, MD, USA;
7
Yale Univ., New Haven, CT, USA; 8Institut de Physique du Globe de Paris, Paris, France.
Introduction: Evidence suggests that ancient Mars
exhibited a core dynamo that shutoff by ~4.1 Ga [1].
In contrast, Martian magmatism persisted from Noachian through Amazonian time, as evidenced by the
emplacement of Tharsis ~3-4 Ga and by volcanic eruptions with very young ages inferred from low crater
densities, including a ~100 Ma eruption of Olympus
Mons [2]. Canonical reasoning suggests that dynamo
shutoff due to secular cooling accompanies a nearconcurrent cooling of the mantle, and consequently the
end of melt generation and volcanism. Here we explore the hypothesis that a basal mantle layer enables a
non-canonical thermal evolution of Mars, and could
allow for both the early cessation of the dynamo and
continued melt generation to the present day.
The MaTH:CAMPS project integrates present-day
observations of the geochemistry, magnetism, and geophysical properties of Mars to constrain the past evolution of Mars’ internal structure and thermal state. To
simulate the coupled thermochemical evolution of the
core and mantle of Mars, we develop one-dimensional
models that allow for evolving core compositions and
utilize parameterized convection [3] under endmember initial conditions.
Core: The core model combines the effects of temperature and composition to determine the level of heat
flux out of the core required to sustain the dynamo.
Thermal Model: The dominant power sources for a
core dynamo are thermal convection driven by secular
cooling and compositional convection driven by core
solidification. Compositional convection from core
solidification is inconsistent with an early shutoff due
to convective vigor and duration [4]. A thermallypowered dynamo requires superheated initial core
states to satisfy the minimum heat flux of ~15 mW/m2
across the core-mantle boundary [5].
Mineralogical Model: The core was modeled as a
Fe-Ni-S alloy, constrained by the Fe-FeS phase diagram which was compiled over 21-40 GPa from multiple experimental studies [6,7]. We consider a wide
range of core sulfur contents from 5 wt.% [5] to 25.6
wt.%, which have a large impact on core size and crystallization scheme (freezing temperature), and density
[8]. For low S contents (<12 wt.%), a dense Fe-Ni alloy will first precipitate at the top of the core. As cooling proceeds, the denser solid will ‘snow’ and collect
as a solid inner core. For high S contents (>15 wt.%),
FeS precipitates at the center of the core and rises cre-
ating a solid outer core. At intermediate S contents,
both processes will occur. Potential observations of
core size and density from InSight will narrow the
range of viable sulfur content and in turn determine
mode and degree of crystallization.
Mantle: We tested two initial conditions for Mars:
a ‘hot’ start with a deep magma ocean that extended to
the core-mantle boundary [9], and a ‘cold’ start or
shallow magma ocean that extended only to the midmantle [10]. These two scenarios set the initial temperature profiles of the mantle and the basal layer
composition. At present, we have only considered
three compositional scenarios resulting from magma
ocean crystallization. These are a homogenous mantle
(no layer) resulting from crystallization of complete
magma ocean, a basal garnet layer from a deep magma
ocean, and a basal mélange layer (composed of ringwoodite, garnet, and Fe metal-possibly due to incomplete core formation) that resided beneath a shallow
magma ocean and did not melt.
We constructed a 1-D parameterized convection
model of the mantle consisting of a stagnant ‘lid’, an
upper (or homogeneous) mantle, a basal mantle layer,
and a lookup interface with the core. Mantle physical
properties were calculated for a Dreibus and Wänke
[11] bulk composition using the thermodynamic modeling program HeFESTo [12], and the physical properties of the basal layer were calculated using EOS and
parameters gathered from the literature appropriate for
the desired composition.
Comparison to Observations:
Dynamo cessation: Cessation of a thermally generated dynamo occurs when core heat flow falls below a
critical value (Fig. 1, dashed line).
Figure 1. Mantle model results of heat flux from coremantle boundary for different starting T and layer compositions, calculated independently of the core thermal model.
*Result of coupled core-mantle models with mélange layer.
46th Lunar and Planetary Science Conference (2015)
Within the basal layer, low viscosities and high initial
temperature contrasts (mélange layer; shallow magma
ocean) can produce an early, short-lived dynamo. Conversely, high to uniform viscosities and moderate temperature contrasts (garnet layer or homogenous mantle;
deep magma ocean) act to insulate the core and prevent sufficient heat flow for dynamo generation, requiring unrealistically high core temperatures to generate a dynamo.
Continued mantle melting: Melt fraction (Fig. 2) as
a function of radial layer is determined using the liquidus and solidus formulations of [13,14]. The basal
mélange layer acts as a long-lived heat reservoir that
extends melt production over a significant span of the
Amazonian. A basal garnet layer or a homogenous
mantle result in high melt production in the Noachian,
but little to no melt produced through to the Amazonian.
Figure 2. Mantle model results of mantle melt generation
(when model T is above solidus T).
Mass and Moment of Inertia: Using the mélange
model, mass and moment inertia of Mars are calculated as a function of varying core radius and crustal
thickness (Fig. 3), and in turn compared to known values (blue/red represents low/high misfit). The best fit
model (from the combined misfit of mass and moment
of inertia) gives us a prediction of internal structure
and properties for direct comparison for the InSight
mission in 2016 which will allow us to test our models
of Martian formation scenarios.
Figure 3. Results or model calculations of mass (left), moment of inertia (middle), and normalized misfit (right) for a
fixed crustal density of 2800 kg/m3, a mantle density calculated for a DW composition in HeFESTo, and a mélange
layer consisting of 1/3 ringwoodite+1/3 garnet+1/3 Fe metal.
For a core radius of 1500 km (14 wt.% S), the crust is required to be 120 km thick; thicker than previous estimates
2900.pdf
[15], giving constraints on the basal layer composition (i.e.,
less Fe).
Future Steps:
Core and Mantle: We will work to fully couple the
core and mantle models, and include the effects of core
solidification and parameterized melt migration to the
thermal model. We will also consider the effects of
magma ocean overturn which will place a dense, relatively cool layer at the base of the mantle [16]. We will
test the sensitivity of heat flux and melt production to
the composition and initial temperature we assume.
Surface/Lithosphere: Using a modified lithospheric
stress code [17] we will compare timing of the thermal
and loading stresses inferred from our parameterized
convection model with the timing of observed geologic
features such as wrinkle ridges. The emplacement of
Tharsis will be approximated using predicted melt
production rates.
Atmosphere: Using melt production rates, we will
approximate degassing rates, to couple with a 1-D atmospheric model that will vary initial surface temperatures based on albedo constraints. This will be incorporated as a boundary condition for the lithospheric
code.
Phobos: We will also model the capture of Phobos
around 4 Ga, based on the thermal history derived
from the core-mantle model by calculating Mars' tidal
quality factor (QP). With different QP evolution paths,
we can calculate the average orbital distance of Phobos
through the past 4 Ga and compare with estimates of
Mars’ atmospheric pressure.
Conclusions: Our preliminary models demonstrate
our ability to predict the consequences of different
Martian evolution histories using coupled parameterized convection and different thermochemical models.
We show that a basal layer that consists of a mix of
ringwoodite, garnet, and Fe metal best satisfies the
requirements that the dynamo shutoff at 4.1 Ga and
that melt generation continues to the recent geologic
past.
References: [1] Lillis et al. (2013) JGR, 118, 1488-1511.
[2] Werner (2009) Icarus, 201, 44-68. [3] Stevenson et al.
(1983) Icarus, 54, 466-489. [4] Buffett et al. (1996) JGR,
101, 7989-8006. [5] Williams and Nimmo (2004) Geol., 32,
97-100. [6] Chen et al. (2008) GRL, L07201. [7] Fei et al.
(2000) Am. Min., 85, 1830-1833. [8] Konopliv et al. (2011)
Icarus, 211, 401-428. [9] Elkins-Tanton et al. (2003) MaPS,
38, 1753-1771. [10] Righter and Chabot (2011) MaPS, 46,
157-176. [11] Dreibus and Wänke (1985) Meteor., 20, 367381. [12] Stixrude and Lithgow-Bertelloni (2005) GJI, 162,
610-632. [13] Longhi et al. (1992) Mars, p. 184-208.
[14] Schmerr et al. (2001) LPSC XXXII, #1157.
[15] Baratoux et al. (2011) JGR, 119, 1707-1727.
[16] Elkins-Tanton et al. (2005) EPSL, 236, 1-12.
[17] Banerdt and Golombek (2000) LPSC XXXI, #2038.