1. No category

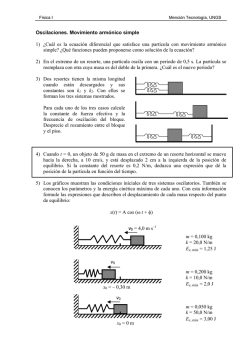
Liceo IBO
Sexto Matemática y Diseño
Problemas “Oscilaciones”
1. La ecuación que describe la aceleración de cierto movimiento es a  C x 2 , siendo x el desplazamiento respecto a
la posición de equilibrio.
a) ¿El movimiento es armónico simple? ¿El movimiento es oscilatorio?
b) Si la aceleración es de la forma a  C x3 , ¿el movimiento es armónico simple? ¿El movimiento es
oscilatorio?
2. Un objeto de masa M está unido a un resorte de constante K, de manera que oscila sobre una superficie
horizontal de rozamiento despreciable, describiendo un movimiento armónico simple. La aceleración máxima del
bloque es de 18,0 m / s 2 y su velocidad máxima 3,0 m / s .
a) Determine la frecuencia de oscilación del bloque y la amplitud de su movimiento.
b) ¿Qué cambios se deben realizar en el sistema para que la velocidad máxima aumente al triple y la
aceleración nueve veces?
3. Un bloque de masa M está unido a un resorte de constante K, de manera que oscila sobre una superficie
horizontal de rozamiento despreciable. Se realiza cierta fuerza F sobre el bloque, estirando el resorte 8,0cm y se
deja libre el objeto desde el reposo.
a) Si tarda 3,0s en llegar a la posición de equilibrio, escriba la expresión para la función x(t ) .
b) Determine los primeros dos tiempos para los cuales el bloque pasa por la posición x  4,0cm .
c) Realice un grafico de la velocidad del bloque en función del tiempo para un período, indicando en qué
tiempos su velocidad es máxima y nula.
4. Un oscilador armónico tiene un período de 0,314s y una amplitud de 7,0cm . En t  0 el objeto se encuentra en
x  A.
a) ¿Qué distancia recorrerá entre t  0 y t  0,063s ?
b) ¿Cuál es la distancia recorrida entre t  0,283s y t  0,345s ?
5. Una diminuta mosca de 0,25g de masa es capturada en la tela de una araña. La telaraña vibra realizando 4
oscilaciones por segundo.
a) ¿Cuál es el valor de la constante de resorte efectiva k para la telaraña?
b) ¿A qué frecuencia se espera que vibre la telaraña si un insecto de 0,50g de masa es atrapado?
6. Un deslizador de 0,50kg se une al extremo de un riel de aire por medio de un resorte de constante k  20 N / m .
El deslizador se desplaza 15cm desde su posición de equilibrio y se suelta, de modo que oscila sobre el riel.
a) ¿Cuál es la máxima aceleración del deslizador?
b) ¿Cuál es la aceleración en un tiempo igual a un octavo del período del oscilador?
c) ¿Cuál es la posición en un tiempo igual a un octavo del período del oscilador?
7. Un cuerpo unido a un resorte oscila según indica el gráfico adjunto:
a) ¿Cuánto vale la amplitud del movimiento?
b) ¿En qué instantes la fuerza neta sobre el cuerpo es nula?
c) Realice el gráfico x(t ) correspondiente.
Liceo IBO
Sexto Matemática y Diseño
8. a) Un sistema masa resorte oscila con una frecuencia de 1,20Hz cuando se cuelga una pesa de masa M de un
resorte de constante K. ¿Con qué frecuencia oscilará si se sustituye el resorte por uno de constante 3K?
b) ¿Qué sucede con la frecuencia de un péndulo simple si se alarga su longitud cuatro veces?
9. Un objeto de 0,50kg está unido a un resorte de constante K  18,6 N / m , de manera que oscila sobre una
superficie horizontal de rozamiento despreciable. Se estira el resorte 5,0cm y se deja libre el objeto desde el reposo.
a) Determine por dos métodos el módulo de la velocidad del objeto cuando el resorte está estirado 2,0cm .
b) ¿Cuántas veces habrá pasado el bloque, por la posición de equilibrio, 5,0s después de haberla soltado?
10. Imagine que lo capturan unos extraterrestres, lo meten en su nave y lo duermen con un sedante. Tiempo
después, despierta y se encuentra encerrado en un compartimento pequeño sin ventanas. Lo único que le dejaron es
su reloj, su anillo y su largo collar. Explique cómo podría determinar si todavía estuviera en la Tierra o si habría sido
transportado a Marte.
11. Un objeto de 2,0kg está unido a un resorte de constante K  10N / m . El sistema se conecta a un amortiguador,
de forma tal que el conjunto tiene asociado un coeficiente de amortiguamiento   0,80s 1 . Se separa al objeto una
distancia A de la posición de equilibrio y se libera.
a) Determine el período de la oscilación amortiguada.
b) Si 0,50s después de haber comenzado la oscilación, la posición del objeto es x  0,060m , determine A.
12. Un péndulo simple se desplaza a una pequeña distancia de su posición de equilibrio y se suelta. Luego de haber
transcurrido 80 oscilaciones en un lapso de 120 segundos, la amplitud del movimiento es la mitad del valor inicial.
Determine el coeficiente de amortiguamento  .
13. ¿Por qué en algunas ocasiones se oyen vibraciones al conducir un vehículo a determinada velocidad, pero estas
mismas desaparecen cuando se conduce más rápido o más lento?
14. Al diseñar estructuras en una región de alta sismicidad, ¿qué relación debe haber entre las frecuencias naturales
de oscilación de una estructura y las frecuencias típicas de terremoto? ¿Por qué? ¿La estructura debe tener mucho o
poco amortiguamiento?
15. Una persona de 80kg viaja en un fusca cuya masa es de 1520kg . El auto se soporta mediante cuatro resortes,
cada uno con una constante de 7,0 104 N / m .
a) ¿Cuál es la frecuencia natural de oscilación de este sistema?
b) El auto comienza a vibrar al pasar sobre los pozos de una calle. Si los pozos están separados 12m , ¿a qué
velocidad se tiene que desplazar el auto para vibrar con la mayor amplitud posible?
Algunos resultados:
2. a) A  0,50m , f  0,95Hz . 3. a) x(t )  0,08cos(0,52t ) , b) t  2,0s , t  10s . 4. a) 0,049m , b) 0,026m . 5. a)
K  0,16 N / m , b) f  2,8Hz . 6. a) amax  6,0m / s 2 , b) a  4,2m / s 2 , c) x  0,11m . 7. a) A  0,32m , b) t  0 ,
t  1,57s y t  3,14s . 8. a) f  2,08Hz , b) La mitad de la anterior. 9. a) v  0,28m / s , b) 10 veces. 11. a) T  3,0s ,
b) A  0,18m . 12. a)   5,8 103 s 1 . 15. a) f  2,1Hz , b) v  25m / s .