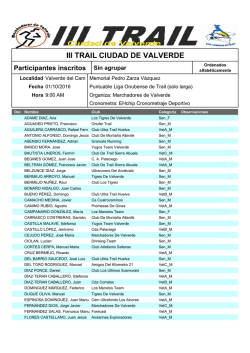
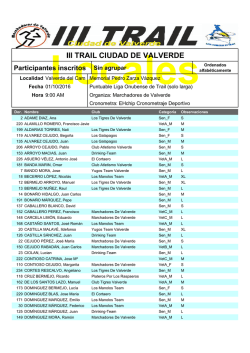
∑∞ =∑∞ ∑ ∑ ∑ ∑∞
Juegos con matrices Veamos una curiosidad matemática. En la página web de nuestra organización, Sigma Society, vi un día un apartado que ponía “curiosidad matemática”. En él se demostraba que si elevamos la unidad imaginaria i = − 1 a ella misma obtenemos un número real. Es más se llega a la conclusión de que ii = e-π/2. Para llegar a esa conclusión tenemos que usar la conocidísima fórmula de Euler, que a decir de muchos es más bella fórmula de las matemáticas: eiπ + 1 = 0 Pero es que el análisis matemático nos permite aún más. La definición del número e en xn desarrollo en serie de potencias de la forma e = ∑ nos permite encontrar el valor de n = 0 n! x i 1 1 1 1 ∞ . Para calcular esto necesitamos calcular la potencia n ésima de la matriz, que n 1 1 1 1 = 2 n −1 Resultado al que se puede llegar fácilmente y que se puede es: 1 1 1 1 n n n −1 i π 1 1 iπ 1 1 ∞ 2 1 1 2 1 1 2 n 1 1 =eiπ 1 / 2 1 / 2 .Usando la demostrar por inducción. i =e =∑ 1 1 1 / 2 1 / 2 n! n =0 iπ formula de Euler tenemos que e = -1 y por tanto: i 1 1 1 1 − 1/ 2 − 1/ 2 . − 1/ 2 − 1/ 2 = Pero no sólo eso. Además podemos realizar cálculos tan exóticos como el seno de una 1 1 En efecto: 1 1 matriz. Por ejemplo el seno de la matriz anterior: Sen ∞ 1 1 ∞ (−1) n 2 2 n −1 (−1) n −1 1 1 = ∑ sen =∑ 1 n =1 ( 2 n − 1)! 1 1 1 n =1 (2n − 1)! 2 n −1 ∞ =∑ n =1 (−1) n −1 2 n − 2 1 1 = 2 (2n − 1)! 1 1 1 1 1 ∞ (−1) n −1 2 2 n −1 sen(2) 1 1 ∑ . Por tanto la expresión que buscamos es: = 2 1 1 n =1 (2n − 1)! 2 1 1 sen(2) 1 1 2 = sen 1 1 sen(2) 2 sen(2) 2 . Donde sen(2) = 0,4546... sen(2) 2 2 Desde aquí doy gracias al gran Euler, hijo predilecto de las Matemáticas, que tanto aportó a la, como decía Gauss, “reina de las ciencias”.
© Copyright 2026












![Libros de texto para o curso 2015/2016 [ pdf ]](http://s2.esdocs.com/store/data/001317105_1-cf6a820cb38ed12fe7d13c8180e3ddc9-250x500.png)