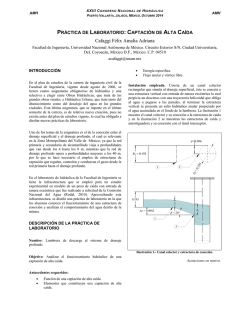
creación de un sistema de información hidrológico para el cálculo
XXIII C ON G R E S O N A C I O N A L AMH DE H I D R Á U LI C A AMH PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 CREACIÓN DE UN SISTEMA DE INFORMACIÓN HIDROLÓGICO PARA EL CÁLCULO DE INTENSIDADES MÁXIMAS Y GESTIÓN DE DATOS METEOROLÓGICOS Merlos Villegas Fidelmar, Sánchez Quispe Sonia Tatiana y Almanza Campos Jorge Alfonso Departamento de Hidráulica, Universidad Michoacana de san Nicolás de Hidalgo. Avenida Francisco J. Mujica S/N, Ciudad Universitaria, Col. Felicitas del Río, Morelia, Michoacán, C.P. 58030 [email protected], [email protected], [email protected] Introducción existencia de los datos pluviométricos es mayor; aunque frecuentemente los datos no tienen una calidad óptima. En el presente trabajo se expone el desarrollo de un nuevo software denominado SIHIMax en versión 1.0.0, el cual está destinado a la gestión de datos climatológicos y la generación de curvas IDF( Intensidad-Duración-Frecuencia). El proceso óptimo es el de construcción (ya que se hace a partir de datos pluviográficos) el problema radica entonces en la escases de pluviográfos en el país, por lo cual en la mayoría de los estudios se recurre al proceso de estimación. Dicho proceso se esquematiza en el siguiente diagrama: En la situación actual de la aplicación de la hidrología en México, sin duda podemos identificar claramente la necesidad de modernizar y optimizar los procesos para la realización de los estudios hidrológicos. La falta de desarrollo de software especializado en este ámbito es por demás destacable, tanto en la parte de la gestión de los datos como en la generación de las curvas intensidad - duración – periodo de retorno. En la realización de los estudios de gasto máximo posiblemente la parte más importante es la obtención de la lluvia de diseño, la cual depende directamente de las curvas IDF. Por esta razón se ha desarrollado una aplicación que pretende facilitar a los hidrólogos los procesos que van desde la ubicación de las estaciones climatológicas hasta la generación de mapas de intensidades. Como resultado se ha desarrollado de manera efectiva una plataforma similar a la de los sistemas de información geográfica, incluso trabajando con formatos correspondientes a estos, con el objetivo de que el usuario se familiarice con la interfaz de una manera rápida. Dicho software es capaz de ubicar las estaciones climatológicas (para México), evaluar la consistencia de los datos, estimar datos faltantes y generar isolineas de intensidad. Marco Teórico Se entiende por curva I-D-F a la relación que existe entre la intensidad de lluvia media, su duración la frecuencia de ocurrencia (inverso del período de retorno).Cabe mencionar que en el país comúnmente se les denomina “Curvas I-D-Tr”. A partir de estas curvas se obtiene la tormenta de diseño con la cual se dimensionan las diferentes obras civiles que sirven para el aprovechamiento del líquido vital y la prevención de inundaciones. Para la obtención de las curvas IDF existen dos metodologías básicas: Construcción(la cual se realiza a partir de datos pluviográficos) Estimación(se realiza con datos de precipitaciones máximas diarias PMD) Aunque lo ideal es que se aplique la primera metodología lo cierto es que no siempre se cuenta con datos disponible para la aplicación de la misma, en cambio la disponibilidad y Ilustración 1.- Proceso para la estimación de las curvas I-D-F. En los siguientes apartados se describen brevemente las faces principales del proceso. Evaluación de Consistencia Una serie de datos meteorológicos se considera consistente siempre y cuando cumpla con las condiciones de: Aleatoriedad, Homogeneidad, Independencia y Estacionalidad. Estas condiciones se describen en la tabla 1 junto con las pruebas correspondientes a cada una. Tabla 1 Evaluación de Consistencia. Condición Descripción Pruebas Aleatoriedad Significa que las fluctuaciones de la variable meteorológica a considerar se deben a causas naturales. No se disponen de pruebas adecuadas para series hidrológicas Homogeneidad Se cumple si todos los valores que conforman la muestra, provienen estadísticamente de una misma población. Test de Helmert Test de Secuencias Test de t Student Test de Cramer XXIII C ON G R E S O N A C I O N A L AMH DE H I D R Á U LI C A PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Condición Descripción Pruebas Independencia Implica que la probabilidad de ocurrencia de uno cualquiera de ellos no depende de la ocurrencia del o de los valores precedentes. Test de Anderson Test de Speaman Estacionalidad Significa que, excluyendo las fluctuaciones aleatorias, la serie de datos es invariante con respecto al tiempo. Test de Man Kendall Corridas de Wolf Wald-Wolfowitz Promedios Móviles de orden 5 Test de Helmert Nos permite comprobar la homogeneidad de los datos mediante un procedimiento sencillo que se consiste en ordenar la serie cronológicamente y analizar el signo de las desviaciones con respecto a la media de cada dato. Si una desviación de un cierto signo es seguida por otra del mismo signo, entonces se dice que se forma una secuencia: S, de lo contrario se considera un cambio: C. Para comprobar que la serie es homogénea se aplica el siguiente criterio: (1) AMH : son la media y la varianza de la primera parte del registro de tamaño El valor absoluto de se compara con el valor de la distribución t de Student de dos colas y con grados de libertad y para un nivel de significancia: α= 0,05. Si y solo si el valor absoluto de es mayor que aquel de la distribución t de Student, se concluye que la diferencia entre las medias es evidencia de inconsistencia, y por ende la serie se considera no homogénea. En caso contrario la serie es Homogénea. Test de Cramer La prueba compara el valor del registro total con cada una de las medias de los bloques elegidos. Para que se considere la serie analizada como estacionaria en la media(homogénea), se deberá cumplir que no existe una diferencia significativa entre las medias de los dos bloques. Si se analiza solamente una muestra (3) (4) (5) Test de Secuencias Esta prueba consiste en analizar el signo de las desviaciones con respecto a la mediana muestral para cada dato y comparar el número de cambios de signo con el número de cambios permitido en base al tamaño de la muestra. Si el número de cambios esta entre los valores establecidos la serie es homogénea. El Test de Mann-Kendall (6) El estadístico tiene distribución t de Student de dos colas con grados de libertad y para un nivel de significancia α = 0,05. Test de Anderson Es un test no paramétrico, estadísticamente basado en el número de orden de las variables y puede ser utilizado para tendencias en series de tiempo de datos hidrológicos si una de esas variables es el tiempo y tiene la particularidad de presentar una mayor potencia estadística en la medida que la serie de datos presenta un mayor sesgo que la aleje de una distribución normal. Test “T” de Student Si se considera una serie de datos de tamaño n la cual de divide en dos partes , entonces el estadístico para esta prueba se obtiene con la expresión: (2) Para una serie independiente la población del correlograma es igual a cero para .Sin embargo series temporales independientes, presentan variabilidad de la muestra, conteniendo fluctuaciones de alrededor de cero, pero estos no son necesariamente cero. En este caso lo que hacemos para determinar los límites de probabilidad de series independientes, utilizamos los límites de Anderson para un 95% de nivel de confianza. (7) Si menos del 10% de los valores de autocorrelación calculados superan los límites, se dice que la serie de datos es independiente. Corridas de Wald-Wolfowitz Dónde: : son la media y la varianza de la primera parte del registro de tamaño Los procedimientos estadísticos paramétricos consisten en la aplicación de ecuaciones matemáticas que tienen como condición necesaria la existencia de una particular y reconocida distribución de la población. XXIII C ON G R E S O N A C I O N A L AMH DE H I D R Á U LI C A AMH PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Para probar la aleatoriedad, la hipótesis nula es: El proceso que genera el conjunto de datos numéricos es aleatorio. La hipótesis alternativa: El proceso que genera el conjunto de datos numéricos no es aleatorio. Procedimiento de la prueba: -Dividir la muestra en dos partes, tomando como valor de referencia la media. -Determinar el estadístico Z: (8) (9) Regresión Lineal Simple Método del U.S. Weather Service Relación Normalizada En este apartado cabe destacar que se puede crear una estación ficticia basando Método del U.S. Weather Service Este método también es conocido como el método del inverso de la distancia al cuadrado y se basa en una metodología fundamentada teórica y empíricamente, la cual se ha posicionado como una de las mejores y más comunes para el completado de series de precipitación. (12) La desviación estándar de R es: (10) (13) Prueba de Spearman Donde: Esta prueba permite evaluar el grado de asociación que tienen los datos de una serie. Las hipótesis de la prueba son: Si la hipótesis se cumple no se tiene una asociación entre los datos de la serie, es decir la condición de independencia se cumple. Si la hipótesis se cumple probablemente existe una asociación entre los datos de la serie, es decir la condición de independencia no se cumple. La fórmula para calcular el estadístico es: . Método de la Relación Normalizada Este es uno de los métodos más simples para completar series climáticas a nivel mensual y anual, y consiste en multiplicar la precipitación de cada estación por el cociente de los promedios de la serie de trabajo y la auxiliar. (11) (14) Donde: Cuadrado de la diferencia de los rangos. Donde: Numero de datos de la serie Después de obtener el valor del estadístico este se compara contra el de la distribución t de Student para un intervalo de confianza de 0.05. Promedios Móviles El análisis con promedios móviles se realiza en forma gráfica. Las series cronológicas de precipitación anual generalmente se analizan con N=5, si se analiza con un N muy bajo se pierde efectividad pues no se reduce la variabilidad, en cambio sí N es muy grande se corre el riesgo que se oculten algunos componentes como la cíclica. Por medio de una línea recta se unen los datos de los periodos secos y de los periodos húmedos y los que varían mucho sobre la media, son probablemente errores en la toma o captura de los datos; analizando así de forma visual la homogeneidad de la serie. Estimación de Datos Faltantes Para la estimación de datos faltantes en las series climatológicas la aplicación utiliza las siguientes metodologías: Regresión Lineal Simple Este es el método de llenado más difundido por su sencillez, se plantea que existe una relación lineal entre los datos de una estación y otra, de manera que: (15) Donde: “m” y “b” son parámetros correspondientes a la ecuación de la recta. P es la precipitación en la estación auxiliar. XXIII C ON G R E S O N A C I O N A L AMH DE H I D R Á U LI C A AMH PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Funciones de Distribución El análisis de frecuencia de valores extremos se desarrolla para estimar los valores máximos asociados a diferentes períodos de retorno de datos como por ejemplo las lluvias máximas registradas en una estación pluviométrica o pluviográfica, o bien los caudales máximos anuales de un río. Considerando una serie de datos, el análisis de frecuencia de la misma se emplea para proveer la magnitud de un evento de cierto período de retorno T, por medio del ajuste de una distribución de probabilidad, la cual se selecciona como la mejor entre un grupo de ellas. (Escalante Sandoval, 2005). El programa incluye la posibilidad de aplicar un análisis regional de frecuencias mediante el empleo de las funciones de distribución indicadas en la tabla II, calculando los parámetros de las mismas por Momentos, Momentos L, Máxima Verosimilitud y Máxima Entropía. . Tabla II.- Funciones de Distribución. Nombre Normal Estandarizada Log-Normal Gumbel Exponencial Gamma Doble Gumbel Función XXIII C ON G R E S O N A C I O N A L AMH DE H I D R Á U LI C A AMH PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Relación entre la precipitación veinticuatro horas y la correspondiente a una hora Para obtener la relación de la precipitación máxima veinticuatro horas (obtenida por medio de funciones de distribución) se utiliza la siguiente gráfica, para lo cual se requiere obtener el número de días con tormentas conectivas y la precipitación media de las máximas diarias. Para Tr menores a 100 años y duraciones menores a dos horas Bell tambien presenta su formula adaptada a una precipitacion de una hora con periodo de retorno de dos años. (18) Modelo de Chen Campos (1998) sugirió un procedimiento que combina la gráfica presente en la ilustración 4 para obtener los factores R y F, necesarios para aplicar la fórmula de Chen (19) (20) Se pueden estimar hasta seis valores del cociente R, uno para cada periodo de retorno procesado para formar la relación regional, para obtener su promedio. Campos-Aranda (2010) ha sugerido emplear tres para estimar el valor de R, los de periodos de retorno de 10, 25 y 50 años. (21) Ilustración II.- Factor R. (16) Donde a, b y c son parámetros función del cociente R; sus expresiones se pueden consultar en Campos-Aranda (2010); está en mm/h; y en mm; t, en minutos (5 ≤ t ≤ 1 440), y Tr (5 ≤ Tr ≤ 100) en años. Los valores calculados de Modelos de Estimación permiten dibujar las curvas IDF. Una vez que se aplica en análisis regional de frecuencias se pueden estimar las curvas IDF por distintas metodologías, de las cuales la aplicación incluye: Interpolación Potencial Modelo de Bell Modelo de Cheng Modelo Emil Kuching Modelo Emil Kuichling y C. E. Gransky Uno de los métodos más antiguos, data de finales del siglo XIX, el cual requiere conocer el tiempo de concentración de la cuenca y la precipitación máxima 24 horas. Su ecuación es: (22) (23) Donde: Hp = Precipitación máxima 24 horas Método de Interpolación Precipitacion asociada a una duración Este método es el más simple, consiste en encontrar la intensidad con una duración de veinticuatro horas (mediante el análisis de distribución de Frecuencias) y mediante el coeficiente R la precipitación con duración de una hora. Posteriormente se hace un ajuste de tipo potencial con los dos puntos anteriores para construir la gráfica. e = Parámetro adimensional que depende del tiempo de concentración A pesar de que es el método más simple tiene validez para cualquier periodo de retorno a diferencia de los anteriores. La aplicación se ha diseñado para que trabaje con distintas bases de datos, de los cuales por su fuente se distinguen dos tipos: Modelo de Bell Este modelo fue desarrollado por Frederich Bell y permite calcular la lluvia máxima asociada a un periodo de retorno y una duración de tormenta, usando como parámetro la lluvia de una hora de duración y 10 años de periodo de retorno. La ecuación que representa el modelo es: (17) d = Duración para la cual se calcula la precipitación Bases de datos Base de datos Primaria: Es un extracto de la base de datos climatológica oficial del país, conocida como “CLICOM”. Base de datos Secundaria: Es un extracto de la base de datos climatológica generada por el IMTA e incluida en el programa ERIC 3. XXIII C ON G R E S O N A C I O N A L AMH DE H I D R Á U LI C A PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Las cuales contienen meteorológicos: los siguientes AMH parámetros Precipitación Evaporación Temperatura Observada Temperatura Máxima Temperatura Mínima Días con Tormenta Eléctrica Días con Granizo Días con Neblina Cobertura Nubosa (Cobertura de Cielo) Precipitaciones Máximas Diarias(PMD) En cuanto a los parámetros de tiempo: Diaria Mensual Anual Adicionalmente se han definido parámetros de tipo de serie: Totales Máximos Mínimos Medios Vacíos Número de días con Tormentas Convectivas (datos mayores a 1mm) Estas bases se pueden trabajar en forma local o en forma remota desde el servidor del programa. Ilustración V.- Configuración del proyecto. Una vez configurado el proyecto se procede a realizar la búsqueda de estaciones en la zona de estudio obteniendo lo siguiente: Ejemplo de Aplicación y Validación Para la validación del programa se han estimado los hidrogramas de cuencas que cuentan con estaciones hidrométricas y las tormentas generadas con las intensidades arrojadas por el programa, a continuación se muestra un ejemplo utilizando la estación hidrométrica de Badiraguato para calibrar. Ilustración VI.- Visualización de las estaciones en la zona de estudio. El programa permite al usuario efectuar pruebas de consistencia tanto graficas como numéricas como se muestran en las siguientes figuras: Al iniciar el programa aparecerá en la pantalla del ordenador la siguiente interfaz: Ilustración VII.- Ejecución de pruebas de consistencia numéricas. Ilustración III.- SIHIMax Previwe. Para crear un nuevo proyecto basta con ir a la opción “Archivo\Nuevo Proyecto” de la barra de menú con lo cual se activara la ventana de visualización de temas. Sin embargo debe configurar el proyecto para que sea guardado satisfactoriamente. Una vez iniciado el nuevo proyecto se configura la aplicación como se muestra en la figura IV donde se eligen las rutas, parámetros de depuración, periodos de retorno y unidades. Ilustración VII.- Ejecución de pruebas de consistencia visuales. AMH XXIII C ON G R E S O N A C I O N A L DE H I D R Á U LI C A PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Para completar series de datos el programa cuenta con una interfaz sencilla pero que permite al usuario elegir los parámetros a utilizar para el mismo, como se muestra en la siguiente ilustración: AMH Es posible visualizar las intensidades mediante la siguiente ventana en forma gráfica: Ilustración X.- Curvas I-D-F. Ilustración VIII.- Llenado de Datos. El programa cuenta con una interfaz accesible para el ajuste de funciones de distribución, calculando la mejor por medio del error cuadrático. Finalmente mediante la aplicación de diagramas de Veronoi se obtiene finalmente el mapa de curva IDF, como se muestra en la figura XI, posibilitando a la vez al usuario la obtención de mapas de curvas PDF (Precipitación-Duración-Frecuencia). Ilustración XI.- Mapa de Curvas I-D-F. Ilustración IX.- Funciones de Distribución. Una vez obtenidas las isoyetas de intensidad se procedió a forma de validación a calcular el hidrograma de la avenida para la estación Badiraguato. Obteniendo la siguiente comparación entre el gasto de la estación hidrométrica y el obtenido mediante la estimación de las curva IDF para un periodo de retorno de 1000 años. Ilustración XII.- Validación. XXIII C ON G R E S O N A C I O N A L AMH Conclusiones y Resultados DE H I D R Á U LI C A PUERTO VALLARTA, JALISCO, MÉXICO, OCTUBRE 2014 Es necesario buscar la manera de mantener los datos actualizados, ya que de ello depende en gran medida la aceptación que tenga la aplicación en la comunidad hidrológica. La plataforma generada tiene un gran potencial para la expansión hacia funciones de generación de gastos y evapotranspiraciones; por lo que es conveniente que en la versión posterior del software se incluya. La herramienta generada puede ser de gran ayuda en la elaboración de una investigación detallada sobre la efectividad de los métodos. La aplicación que se ha desarrollado tiene la capacidad de: Visualizar archivos en formato Shapefile, incluyendo la base de datos del formato Localizar geográficamente las estaciones climatológicas mexicanas Descargar las series pertenecientes a las estaciones descargadas Importar estaciones desde un formato CSV, esto para aumentar el rango de aplicación al no depender únicamente de las estaciones climatológicas mexicanas Creación de archivos vectoriales para almacenar la ubicación espacial de las estaciones Calcular parámetros estadísticos básicos de las series(media, mínimo, máximo, desviación estándar, sesgo) Calcular y visualizar matrices auxiliares para el llenado (correlación lineal, distancia euclidiana, distancia Planar, variación del a precipitación media anual entre estaciones) Evaluar la consistencia de las series de tiempo Estimar datos faltantes de las series Generar nuevas series a partir de las existentes Aplicar un análisis de distribución de frecuencias a las series seleccionadas Estimar, auxiliándose del análisis de distribución las intensidades de diseño asociadas a un periodo de retorno y duración (Curvas IDF) Visualizar las intensidades estimadas forma gráfica, numérica y espacial. BIBLIOGRAFÍA Watt (1989), “Hydrology of floods in Canada: a guide to planning and design”, Consejo Nacional de Investigación de Canadá, Ottawa, 245 pp. Campos Aranda (2007), “Estimación y Aprovechamiento del Escurrimiento”, San Luís de Potosí, México: Editorial Campos. Escalante Sandoval (2005), “Técnicas Estadísticas en Hidrología”, UNAM, D.F. México. AMH Campos Aranda (2007), “Estimación y Aprovechamiento del Escurrimiento”, Editorial Campos, San Luís de Potosí, México. Campos Aranda (1998), “Procesos del ciclo hidrológico”, Universidad Autónoma de San Luis Potosí. San Luis Potosí, México.
© Copyright 2026