1. No category

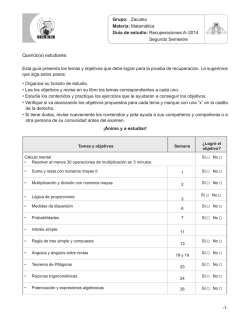
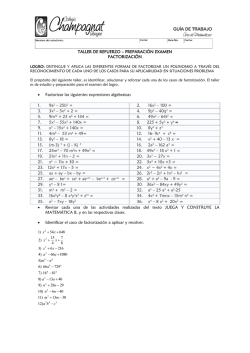
COLEGIO COLOMBO BRITÁNICO
“Formación en la Libertad y para la Libertad”
ÁLGEBRA (TIC)
GRADO:8O
DOCENTE: Nubia E. Niño C. FECHA: 21 / 07 / 15
Guía Didáctica
3-3
Desempeños:*Identifica el caso o los casos de factorización que contiene un polinomio.
* Factoriza polinomios en los cuales se combinan dos o más casos de factorización.
* Comprende y aplica la factorización como un recurso algebraico necesario para simplificar expresiones algebraicas
complejas.
APRENDE:
FACTORIZ ACIÓN :
Ca so # 4 : Factorización de Binomios - Su m a y dif er en ci a de cubo s La su ma d e cu bos s e
des c om po n e en dos f a c tor es , el pr im er f ac t o r c o nt i e ne la s um a d e l as r aíc es c ú b ic as de c ad a
tér m i no y e l s e gu n do f ac t or es u n tr i nom i o c u yos t érm in os s o n e l c ua dr a do d e l a pr im era raí z
c úb ic a, m en os e l pr od uc t o d e l as r aíc es c ú b i c as , m ás e l c u a dra d o de la s eg u nd a ra í z c ú b ic a , es
dec ir :
3
3
2
2
a + b = (a + b) (a – ab + b )
3 6
; Ejemplo: 27x y + c
12
2
4
2 4
4
2
8
= (3xy + c ) (9x y – 3c xy + c )
La diferencia de cubos se factoriza como el producto de dos factores, e l pr im er f ac t or c o nt i e ne la r e s ta d e
l as r aíc es c ú b ic as de c ad a t ér m in o y e l s e g u nd o f ac t or es u n tr i no m io c u yo s t érm in os s o n e l
c ua dr a do d e l a pr im er a r aí z c úb ic a, m ás e l pro d uc t o d e l as r a íc es c ú b ic as , m ás e l c u adr ad o d e l a
s eg u nd a ra í z c ú b ic a , e s d ec ir :
3
3
2
2
a – b = (a – b) (a + ab + b )
3 6
9 12
2
3 4
2 4
2 3 4
6 8
; Ejemplo: 64a b – 27x y = (4ab – 3x y ) (16a b + 12ab x y + 9x y )
Ca so # 5 : Factorización de Binomios – Suma o diferencia de potencias de igual exponente. E n f o r m a
ge n er al , u na s um a o d if er enc i a d e p ot e nc i as i g ua l es s e f ac t or i za c om o e l pr o duc t o de un
b in om io y u n po l i nom i o.
Cu a nd o es div is ibl e p or a + b , e l pr im e r f a cto r es a + b, los s ig n os d el seg undo f act or s e
a lt ern a n + , –, + , …
Ej e mpl o :
n
n
n-1
n-2
n-3 2
5
4
3
2
a + b = ( a + b) ( a – a b + a b – …) ; x + 32 = (x + 2)  (x – 2x + 4x – 8x + 16)
Cu a nd o es div is ibl e p or a – b , e l p r im er f a cto r es a – b , l os s i g n os d el seg undo f act or s o n
pos i t i vos p ar a t od os l o s t ér m in os .
Ej e mpl o :
n
n
n-1
n-2
n-3 2
n-1
6
6
5
4
3 2
2 3
4
5
a – b = ( a – b) ( a + a b + a b +… + b ); x – y = (x – y)  (x + x y + x y + x y + xy + y )
APLICACIÓN:
NOTA  Todo el taller se desarrolla en el cuaderno; mostrar proceso y dar claramente la(s) respuesta(s).
Trabajar ordenadamente.
ACTIVIDADES:
Para cada ejercicio realice el proceso que justifique su respuesta.
1) Factorizar las siguientes expresiones, aplicando los casos vistos hasta el momento, nombrar el caso o los
casos que se aplican en cada ejercicio:
3
3
h)
125
x 3 + 27
8
3
3
3
3
z3)
z8)
729
125
1
81
3
4
o) a + 8a
6
9
x) 27m + 64n
m12 𝑛6 𝑝3 +
m4 – n8
3
1
64
z9)
m3 𝑛9
1
32
2
6
3
9
12
j) x y + 125 x y
6
p) m – x
36
3
q)
9
y) 1 – 27r w
z4) 128
x 5 – y10z15
3
d) 3x – 27
c) 24x + 3
i) 8m – 27n
ñ) x + y + 2x + 2y
u) 8x – 125
3
b) 64a – b
a) 5x + 40
1
16
k)
1
8
x6 − 1
x4 − y8
z) 343x
3a
l)
1
3
6b
– 512y
z10) (2𝑚 − 𝑛)3 − 27𝑚3
z1)
x 6 − 64𝑦 12
5
5
27
m3 − 8
3
3
m) 3x + 81
t) 2x + 64
5
z2) x – 243
2
2
3
z6) x + 2x + 2xy + 2y – y
2
z10) 125 – (3a + 1)
6
5
s) 3m – 3n
64
g) 64 – x
f) w + 1
343
r) 5x + 5
+ x7 z5) 4m9 – 32n3x6
5
e) 2x – 16
10
z7) y – 32w
3
2) Determina el polinomio que representa el perímetro de la figura y factorízalo:
3) Escribir qué le hace falta a cada expresión para ser factorizada como una suma o una diferencia de cubos. Luego,
acomodar condiciones y factorizarlas.
12
a) 1 + 4n
2
b) y – 8w
3
c) 4 + 27x
6
d) 9 – 125x
3
3
e) m + 4
4) Escribir V, si la expresión es verdadera o F, si es falsa y justifica tu respuesta.
5
5) Construye un rectángulo a partir de las piezas que componen la figura. Hallar las longitudes de los lados y el área
correspondiente. (Aplicar factorización).
6) Determina el volumen del siguiente sólido y factoriza.
Fuentes Bibliográficas:
B al d or , Au re l i o. Ál g eb r a E l em ent a l, Ed i to ri a l M e di t errá n e o, 1 9 71
Ru e da L a R ot a, F er na nd o y O tr os . N ue v as Ma t em átic as 8 , E d it or i a l S an t il l a na , 2 00 7
Bello, Ignacio. Álgebra, Thomson Editores, 2004
Rubiano Cifuentes, Julián. Hipertexto 8, Editorial Santillana, 2010
https://aula.tareasplus.com/Roberto-Cuartas/Algebra-Elemental/Casos-de-factorizacion-suma-y-diferencia-depotencias-iguales
Nubia Esmeralda Niño Cárdenas
Bustos Mancera, Luis Alejandro y otros. Zoom 8, Editorial Libros y Libros, 2012
Imágenes de: Rubiano Cifuentes, Julián. Hipertexto 8, Editorial Santillana, 2010
Nubia Esmeralda Niño Cárdenas
Ru e da L a R ot a, F er na nd o y O tr os . N ue v as Ma t em átic as 8 , E d it or i a l S an t il l a na , 2 00 7
https://aula.tareasplus.com/Roberto-Cuartas/Algebra-Elemental/Casos-de-factorizacion-suma-y-diferencia-depotencias-iguales
es.tiching.com/file/download/a32747cb28b1357ea556fcf212c7138a
Bustos Mancera, Luis Alejandro y otros. Zoom 8, Editorial Libros y Libros, 2012
“Si tieneS un porqué para vivir encontraráS caSi Siempre el cómo”
Nietzsche