1. No category

Curso: Álgebra II, UMCE
Profesor: William Campillay Llanos
Prueba 2
27 de Mayo, mes del trabajador
Introducción a la Teorı́a de Grupos.
Nombre:
¡Recuerde! responda en forma ordenada. Cada pregunta tiene una nota de 1
a 7, la nota final es el promedio de las cuatro preguntas.
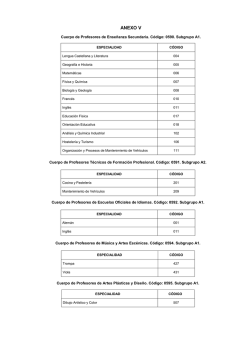
1.- Anillos de Enteros módulo n.
Haga las Tablas para la suma y multiplicación de Z/6Z ¿Por qué le
parece extraño que en la tabla de multiplicación aparezca el producto
2 · 3=0?
Sean a, n ∈ Z, n > 0. Entonces existe un entero b ∈ Z con
ab ≡ 1(mod n) si y solamente sı́ mdc(a, n) = 1
Sea p primo, entonces la únicas soluciones de x2 ≡ 1(mod p) son 1, −1
módulo p.
Sea p un primo, entonces en el mundo Z/pZ tenemos que
(a + b)p = ap + b
p
para cualquier
(Idea: Recuerde el Binomio de Newton
P a, b p!∈ Z/pZ.
(a + b)p = pk=0 ( k!(p−k)!
)ap−k bk )
2.- Grupos:
1. Muestre que todo grupo (G, ∗) con identidad e tal que x ∗ x = e para
todo x ∈ G, es abeliano.
2. Escriba dos grupos No abelianos que le gusten y explique por qué.
3. Sea S el conjunto de todos los números reales excepto −1 (al final diga
por qué no se considera −1). Definase ∗ en S por a ∗ b = a + b + a · b
donde +, · son las operaciones usuales. Muestre que (S, ∗) es un Grupo.
1
3.- Subgrupos:
Si (G, ∗) es un grupo y A, B son dos subgrupos de G y además bAb−1 ⊂
A para todo b ∈ B. Demuestre que AB es un subgrupo de G donde
AB = {a ∗ b | a ∈ A, b ∈ B}
Si (G, ∗) es un grupo y H un subgrupo de G y a ∈ G demostrar que
aHa−1 = {a ∗ h ∗ a−1 | h ∈ H} es un subgrupo de G.
Sea (G, ∗) un grupo, definamos el conjunto
Z(G) = {g ∈ G | g ∗ a = a ∗ g, para todo a ∈ G}
demuestre que es un subgrupo de G ¿Si G es abeliano diga quien es
Z(G)?
4.- Considere el conjunto G de elementos funciones Ta,b : R → R definidas,
para a, b ∈ R se tiene que Ta,b (r) = ar + b, con la operación composición de
funciones ◦. Demuestre que este conjunto, con la operación asociada forma
un grupo. ¿Es abeliano? (Haga todos los detalles).
Dario Salas: Este ilustre educador chileno nace el 09 de Mayo de 1881 en
Baja Imperial, actual Puerto Saavedra. Se titula de Profesor Primario en la
Escuela Normal de Chillán en 1899 y de Profesor de Castellano y Francés en
el Instituto Pedagógico en 1904. En los Estados Unidos se gradúa de Master
en Pedagogı́a en 1906 y en 1907 de Doctor de Filosofı́a y Ciencias de la
Educación.
El significativo aporte de Darı́o Salas a la educación chilena se extiende
por más de tres décadas. Se inicia como ayudante de escuela primaria en
1900. Es Profesor de Pedagogı́a e Idiomas en las Escuelas Normales de Santiago. Profesor de Pedagogı́a en el Instituto Pedagógico, Instituto Superior de
Comercio e Instituto de Educación Fı́sica, Inspector General de Instrucción
Pública, Director General de Educación Primaria, Consejero del Ministerio
de Educación Pública, Profesor de las Cátedras de Historia de la Educación
y de Pedagogı́a y Director de Práctica Pedagógica en el Instituto Pedagógico.
Su último cargo es como Decano de la Facultad de Filosofı́a y Ciencias de la
Educación de la Universidad de Chile, en 1935. En el año 1917, publica su
obra más importante -El Problema Nacional-, Bases para la reconstrucción
de nuestro sistema escolar primario.”
.
2