1. Educación

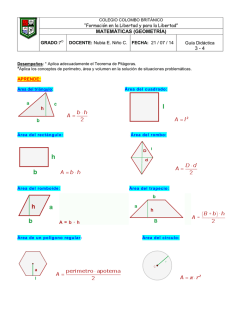
COLEGIO COLOMBO BRITANICO
“Formación en la Libertad y para la Libertad”
MATEMÁTICAS - REPASO SEMESTRAL # 2
DOCENTES: Natalia A. Gil V.
GRADO:7O
Nubia E. Niño C. FECHA: 21 / 10 / 14
TALLER:  4 - 6
Repaso
INDICADOR DE LOGRO: Aplica los conceptos fundamentales del segundo semestre.
ACTIVIDADES:
NOTA  Todo el taller se desarrolla en el cuaderno; mostrar proceso y dar claramente la(s) respuesta(s).
1) Ha l l a r e l á r e a e n m m
resultado es:
2
y en cm
2
de la parte sombreada, en la siguiente figura, el
10m
20m
2
2
2) Hallar el área sombreada en dam y en cm de la siguiente figura:
8m
6m
3 ) El valor de (a + b – c), aplicando la propiedad fundamental de una serie de razones, si
a
b
c
=
=
y (a + b + c) = 32 es:
5
30
45
16
20
4) Aplicando las propiedades de las proporciones en:
=
 si d – b = 20, el valor de b y d
b
d
respectivamente son:
5) Calcular el área del triángulo cuyos vértices tienen por coordenadas (–2,0); (4,0) y (3,3), el resultado es:
6) Un lado de un triángulo mide 7,3cm; el segundo lado mide 1,9cm más que el anterior y el tercer lado mide el
doble que el segundo lado. ¿El perímetro del triángulo en hm es?
7) Al determinar el perímetro en metros de un triángulo rectángulo de hipotenusa 26mm y cateto 24mm, el
resultado es:
2
8) Al calcular el área en dam del siguiente triángulo, sabiendo que x = 2dm el resultado es:
5x
3x
4x
9) Al hallar el perímetro en hm de la siguiente figura, el resultado es:
7m
3m
6m
4m
10) E l n ú m e r o d e d i a g o n a l e s q u e s e l e p u e d e n t r a z a r a u n a ) e n d e c á g o n o ; b ) d e c á g o n o
son:
11) Considere las siguientes afirmaciones:
o
I. En todo triángulo, la suma de los ángulos interiores es 180 .
II. En algunos triángulos al lado de mayor longitud se opone el ángulo de mayor medida.
III. En todo triángulo, la medida de un ángulo exterior es igual a la suma de las medidas de los ángulos que le
son adyacentes.
IV. En todo triángulo, se cumple la desigualdad triangular.
De las anteriores afirmaciones cuales son incorrectas, sustentar la (s) respuesta (s)
12) Un lago circular tiene en el centro un islote de forma circular, como se indica en la figura. Calcular el área
que ocupa el agua (o región sombreada), si el radio del lago circular mide 30m y el radio del islote es 18m
menos que el radio del lago.
13) Hallar el valor de (a + b – c), aplicando la propiedad fundamental de una serie de razones, si
2
a
=
14
b
=
24
c
y (a + b + c) = 60
14) Hallar los valores desconocidos en la siguiente proporción, aplicando la propiedad respectiva
5
30
=
m
n
 si n – m = 80
15) Hallar los valores desconocidos en la siguiente proporción, aplicando la propiedad respectiva.
11
m
=
44
w
 si w – m = 42
16) Plantear la regla de 3 respectiva y resolver.
a) Un atleta de 1,80m de estatura salta 2,20m en salto alto. Si otro atleta de 1,50m de altura pudiese saltar en la
misma proporción, ¿cuánto saltaría?
b) 10 sastres confeccionan 40 vestidos en 8 días. ¿Cuántos días emplearían la mitad de los sastres en elaborar
el triple de los vestidos?
c) Hallar cuántos días puede alimentar José a sus 75 gallinas con 24 kg de alimento, si en el paquete de
alimento se indica que 12 kg alcanzan para 20 gallinas durante 15 días?
d) Una vara de 55 centímetros proyecta una sombra de 15 centímetros. ¿Cuánto mide un poste que proyecta
una sombra de 150centímetros?
e) Una persona ha recorrido 280km, en ocho días caminando 7 horas diarias. ¿Cuántos días tardará en recorrer
540km. andando 9 horas diarias?
f) Una familia compuesta de 6 personas consume en 2 días 3 kg de pan. ¿Cuántos kg de pan serán consumidos
en 5 días, estando dos personas ausentes?
h) Un ciclista marchando a 12km por hora recorre en varias etapas un camino, empleando 9 días a razón de 7
horas por día. ¿A qué velocidad tendrá que ir si desea emplear sólo 6 días a razón de 9 horas diarias?
17) Hallar el perímetro en Hm y en mm del siguiente polígono:
3,3cm
3cm
2,2cm
8,3cm
2,2cm
10cm
18) Ha l l a r e l á r e a e n D m
12dm
2
de la parte sombreada, en la siguiente figura :
8dm
15dm
2
2
19) Hallar el área en m y en dm , del terreno que muestra la siguiente figura:
14mm
2,4mm
10mm
2,4mm
5,2mm
6,1mm
2
20) ¿Cuál es el área de un romboide en dam cuya base mide 30dm y su altura es
5
6
de la base?
21) Si la hipotenusa en un triángulo rectángulo = 5cm y uno de los catetos = 3cm, ¿Cuál es la medida del otro
cateto en m?
22) Determinar cuáles de las siguientes afirmaciones son verdaderas y cuáles son falsas.
a) Un paralelepípedo, es un cuerpo redondo, en el cual las caras opuestas son diferentes. _____
b) Un poliedro de 4 caras, 6 aristas, tiene 12 vértices. ____
c) Los cuerpos de revolución son: pirámide, prisma y un tetraedro. _____
23) Calcular la medida del lado de un cuadrado y el área si su perímetro es 60 cm.
2
24) Calcular el área sombreada en dam de la siguiente figura:
5cm
5cm
15cm
25) ¿Cuánto es la diferencia entre las áreas de una circunferencia de 12 m. de diámetro y otra de 8 m. de
radio?
26) Las bases de un trapecio miden 12 cm. y 21 cm. ¿Cuál es su área si la medida de su altura es igual a la
medida de la base menor?
27) Calcular el área y el perímetro de un rectángulo de 10 cm de base y 6 cm de altura.
28) En el colegio “Mis primeras Letras” el 35% de los estudiantes van de intercambio. Si el colegio tiene 895
estudiantes, ¿Cuántos estudiantes aproximadamente no van de intercambio?
29) Para las elecciones de la personería en un colegio los cuatro candidatos obtuvieron la siguiente votación:
candidato # 1 = 35%; candidato # 2 = 48%; candidato # 3 = 11% y el candidato # 4 = 6%, Calcular la cantidad
de votos obtenidos por cada candidato, si hubo 1000 votos?
30) Un televisor LCD de 32 pulgadas que cuesta $1200000 está en rebaja de un 30%; al pagar en la caja se
añade el 16 % por concepto de IVA. ¿Cuál es el precio final del televisor?
31) Calcular el área y el perímetro de un rombo cuyas diagonales miden 30 y 16 cm, y
su lado mide 17 cm.
32) Calcular el área y el perímetro del siguiente trapecio:
2
33) Calcular el área en m y el perímetro en Hm de un pentágono regular de 6 cm de lado.
2
2
34) Hallar el área sombreada de la siguiente figura en mm y en m .
6dm
35) Los catetos de un triángulo rectángulo miden 2dm y 5dm. ¿Cuántos cm. mide la hipotenusa?, ¿Cuánto mide
el perímetro en m?
36) Hallar el área sombreada en mm de la siguiente figura.
6dm
37) Leer, analizar y resolver los siguientes problemas:(plantear la ecuación); en todos mostrar proceso y dar
respuesta completa.
a) Hallar dos números enteros pares consecutivos cuya suma sea 194.
b) E l c o c i e n t e e n t r e u n n ú m e r o y 5 , a u m e n t a d o e n 8 e q u i v a l e a 2 0 , ¿ C u á l e s e l n ú m e r o ?
c) Buscar un número, sabiendo que la diferencia entre su cuádruplo y la tercera parte del número dado menos 4
es el triple de la suma de la mitad del número dado más 10.
d) Si sumamos 5 unidades al doble de un número el resultado es el mismo que si le sumáramos 7 unidades.
¿Cuál es ese número?
e) L a e d a d d e L u i s e s l a m i t a d d e l a e d a d C a m i l o , s i a m b a s e d a d e s s u m a n 7 5 , ¿ C u á l e s
son las edades?
f) Un padre tiene 49 años y su hijo 11. ¿Dentro de cuánto tiempo la edad del padre será el triple que la edad del
hijo?
g) La base de un rectángulo es doble que su altura. ¿Cuáles son sus dimensiones si el
perímetro mide 30 cm?
38) Calcular el volumen de los siguientes sólidos:
A)
39) Observa la figura 1.
B) r = 3cm y h = 5cm
C)
¿Cuál o cuáles de las siguientes afirmaciones acerca de la figura 1 es o son verdadera(s)?
I. Los lados RS y TU son paralelos.
II. Los lados ST y RU son paralelos.
III. Los lados ST y TU son perpendiculares.
40) En la función de un circo, un malabarista utiliza pelotas de igual forma y tamaño que guarda en una caja: 2
rojas, 4 verdes y 8 amarillas.
El número de posibilidades que tiene el malabarista de sacar una pelota roja de la caja, con respecto a sacar
una pelota verde es:
41) Con bloques como este
Pepito armó el sólido que se muestra en la siguiente figura:
¿Cuál es el volumen del sólido que armó Pepito?
42) A una fiesta infantil asisten 50 invitados. Entre éstos se rifan 5 relojes de juguete, 15 pelotas y 10
rompecabezas. El número de posibilidades de que un invitado gane una pelota, con respecto a ganar un reloj
de juguete es:
43) Una urna contiene 4 bolas rojas, 3 bolas negras y 5 bolas blancas, todas de igual forma y tamaño. Pedro va
a sacar una bola de la urna sin mirar. El número de posibilidades de que la bola que saque Pedro sea roja con
respecto al número de que saque negra es:
44) En el plano cartesiano se ubican tres parejas ordenadas que son vértices de un paralelogramo.
¿Cuál de las siguientes parejas ordenadas puede corresponder al cuarto vértice del paralelogramo? Sustentar
la respuesta.
A. (-3, -1)
B. (5, -2)
C. (11, 1)
D. (14, 1)
45) Un carpintero construye un mueble que tiene cajones como el que aparece en la siguiente figura:
3
¿Cuál es la capacidad en cm de uno de los cajones del mueble?
46) La siguiente tabla representa las calificaciones obtenidas por un grupo de estudiantes universitarios en un
examen
Según las calificaciones obtenidas en el examen, los estudiantes son clasificados como se indica a
continuación:
¿Cuál es la probabilidad de que el estudiante escogido esté clasificado como aprobado?
47) En el siguiente plano cartesiano se muestran las circunferencias C y C’ con centros en O y
O’. Las circunferencias son tangentes en el punto E y O es un punto de C’.
Las coordenadas de O y O’ son (2,2) y (3,2) respectivamente. ¿Cuántas unidades mide el diámetro de C?
48) En la figura se muestra un paralepípedo recto.
¿Cuál de las siguientes afirmaciones no es verdadera? Sustentar la respuesta.
A) Los rectángulos DEHC y AFGB tienen la misma área.
B) El rectángulo ABCD es congruente con el rectángulo FGHE.
C) La medida del segmento DG es igual a la medida del segmento AC.
D) La medida del segmento EA es igual a la medida del segmento CG.
49) Jorge quiere fabricar una cometa en forma de rombo como la que se presenta en la figura, utilizando
plástico y palos de balso.
2
¿Cuántos dam de plástico, mínimo, se requieren para cubrir la superficie de la cometa?
50) La suma de los ángulos interiores de un endecágono es igual a:
2
51) Hallar el área total en m de la siguiente figura es:
52) En el centro de un jardín cuadrado de 150 m de lado hay una piscina tam bién cuadrada, de
2
25 m de largo. Calcular el área en cm del jardín o parte sombreada.
25m
25m25
150m
3
53) Teniendo en cuenta las medidas señaladas, calcular el volumen de esta figura en m :
54) Determinar el valor de los lados desconocidos, si las medidas de los lados correspondientes de los dos
triángulos son proporcionales.
a=3
c=5
b=4
d=6
x
m
O
55) Construir una tabla de frecuencias correspondientes a los datos del peso en Kg de 15 alumnos de grado 7 .
55, 53, 52, 55, 48, 52, 47, 47, 51, 47, 45, 52, 45, 51, 46.
Fuentes Bibliográficas:
http://www.amolasmates.es/cidead/libros/2eso/temas/10Volumen%20de%20cuerpos%20geometricos.pdf
Nubia Esmeralda Niño Cárdenas
http://www.vitutor.com/geo/esp/vActividades.html
http://inst-mat.utalca.cl/tem/sitiolmde/octavo/guiasoctavo/ac_m3_09_cuerpos_geometricos_santillana[1].pdf
http://www.ditutor.com/geometria/area_triangulo.html
http://www.sectormatematica.cl/basica/santillana/areas.pdf
www.icfes.gov.co
http://www.ditutor.com/geometria/perimetro.html
http://www.geoka.net/triangulos/teoerma_pitagoras.html
http://es.scribd.com/doc/32182075/EJERCICIOS-RESUELTOS-DE-AREAS
http://www.vitutor.com/geo/eso/ar_4.html
http://www.vitutor.com/geo/eso/ar_1e.html
http://www.aulafacil.com/matematicas-volumenes/curso/Lecc-1.htm
Rubiano Cifuentes, Julián. Hipertextos 7, Editorial Santillana 2010
http://www.aulamatematica.com/ESO3/PDF_resueltos/E3_3_regla%20de%203%20COMPUESTA_01.pdf
boj.pntic.mec.es/~jherna34/ESO2/.../Regla_de_tres_compuesta.doc
http://aulamiguelturra.weebly.com/uploads/1/1/5/4/11548579/reglasdetrescompuestas1.pdf
Imágenes de: www.icfes.gov.co
http://www.geoka.net/triangulos/teoerma_pitagoras.html
http://www.vitutor.com/geo/eso/s_e.html
http://www.vitutor.com/geo/eso/ar_4.html
http://www.vitutor.com/geo/eso/ar_1e.html
http://wwwgeometriabasica.blogspot.com/2011/11/el-area-de-un-circulo.html
http://www.aulafacil.com/matematicas-volumenes/curso/Lecc-1.htm
“Si tieneS un porqué para vivir encontraráS caSi Siempre el cómo”
Nietzsche