Download Report

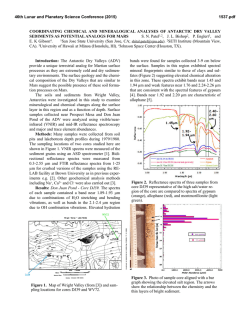
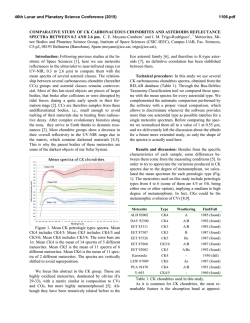
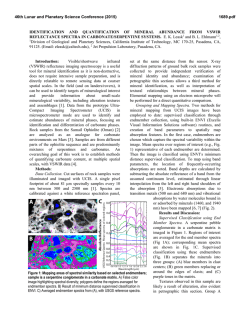
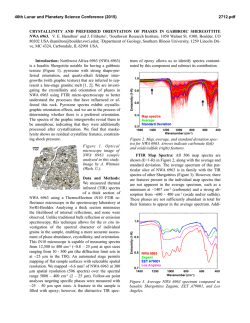
46th Lunar and Planetary Science Conference (2015)
1535.pdf
CALCULATING THE SCATTERING PORPERTIES OF FINE PARTICULATES ON PLANETARY
SURFACES. G. Ito1 and T. D. Glotch1, 1Stony Brook University, 255 Earth and Space Sciences Building, Stony
Brook, NY 11794-2100 ([email protected]).
Introduction: Infrared spectroscopy is a useful tool
for remotely analyzing earth and planetary materials.
Mid-infrared (~5-50 µm) emissivity is particularly
suited for quantitative analysis of bulk silicate mineralogy. Emissivity is dependent on composition, but also
on grain size, shape, and packing density [1,2]. For
coarse particulates, emissivity spectra add linearly.
However, when particulate size is on the order of wavelength of incident radiation, spectra manifest strong
non-linearity that hinders accurate mineralogical interpretations. Major spectral changes that occur as particle
size decreases include reduction of Reststrahlen band
strength, and appearance of transparency features.
These nonlinear effects have been difficult to model,
and therefore, accurate analysis of mineralogy of planetary surfaces composed of fine particulates has been
problematic.
To mitigate this problem, radiative transfer models
have been used to calculate mid-infrared spectra of fine
particulates. Moersch and Christensen (1995) [3] evaluated the effectiveness of different radiative transfer
models using quartz and concluded that a Mie/Hapke
hybrid model best captures the effect of particle size on
mid-infrared emissivity spectra. Mustard and Hays
(1997) [4] further used a Mie/Hapke hybrid model to
construct reflectance spectra of olivine and quartz, and
Pitman et al. (2005) [5] improved on the works of [3]
and [4]. Despite these efforts, Mie/Hapke hybrid model
has not been able to compute spectra that are fully agreeable with laboratory measurements.
Mie theory, incorporated in previous models, provides scattering parameters used to calculate the single
scattering albedo and asymmetry parameter, which are
the necessary parameters for solving radiative transfer
equations. Mie theory is applicable and useful in a sense
that it captures diffraction effects, which occur for particulate sizes on the order of wavelength of incident radiation, but makes an assumption that particulates are
well separated. This assumption is not necessarily met
for planetary studies, such as regolith on the Moon, asteroids and Mars, where particulates are closely packed.
This incongruence of Mie theory assumption with the
actual setting could be the cause of inadequate modeling
by previous studies.
In this work, we avoid this problem and calculate
more accurate spectra using the Multiple Sphere T-Matrix (MSTM) method instead of Mie theory. MSTM directly solves Maxwell’s equations and is well-suited for
multiple scattering caused by many, closely packed particulates such as planetary regolith [6]. Arnold et al.
(2012) [7] and Glotch et al. (2012) [8] have proven the
usefulness of MSTM method. Here, we expand on their
work and highlight the better modeling capabilities of
MSTM method by comparing its mid-infrared emissivity spectra to Mie computed spectra and laboratory acquired spectra.
Methods: As the MSTM method is dependent on
optical constants of minerals, optical constants of three
principle indices of enstatite were first obtained from
Rucks and Glotch (2014) [9]. A cluster of spheres was
generated using a jammed sphere packing algorithm
[10], and averaged optical constants were assigned to
each sphere at every wavenumber of interest in the midinfrared region. For this study, spheres were assigned a
diameter of 10 µm in order to simulate the finest particulates of planetary regolith. Sphere positions, sphere diameter, and optical constants were used as inputs for the
MSTM code developed by Mackowski and Mishchenko
(2011) [11]. This code is designed to run on parallel
computer clusters, and we ran MSTM code on NASA’s
Pleiades cluster located at Ames Research Center.
Once MSTM computed the necessary parameters,
they were input into radiative transfer models presented
by Conel 1969 [12], Hapke (1993) [13], and Hapke
(1996) [14] to calculate emissivity spectra. All three of
these models solve the equation of transfer by the twostream approximation method. We also computed scattering parameters using Mie theory and then input them
into the same three radiative transfer models in order to
provide a direct comparison to the hydrid
MSTM/radiative transfer models.
Finally, same enstatite used to obtain optical constants by [9] was ground into powders. Grain sizes less
than 10 µm were separated out to measure emissivity
spectra using our customized Fourier Transform Infrared Spectrometer. Computed spectra were directly compared with this laboratory spectrum.
Results: Computational and laboratory emissivity
spectra are plotted in Figure 1. Scattering parameters
from MSTM and Mie are input into the three radiative
transfer models and are compared to each other as well
as to the laboratory measurement.
Discussions: The MSTM and Mie methods display
significant differences. Both types of computational
spectra have a tendency to overestimate spectral con-
46th Lunar and Planetary Science Conference (2015)
a.
b.
c.
Figure 1. Computational and laboratory emissivity
spectra of enstatite particulates with diameter of 10
µm or less. Models used in computation are Mie and
MSTM methods coupled with radiative transfer
models of a. Conel (1969), b. Hapke (1993), and c.
Hapke (1996). For each plot, laboratory, MSTM,
and Mie spectra are shown in blue, green, and red,
respectively.
trast compared to laboratory spectra. The MSTM
method reduces this overestimation and performs better
than Mie method. Generally, computational spectra using MSTM more closely follow the laboratory spectrum
1535.pdf
than the Mie-computed spectra for all three radiative
transfer models. An example of a clear distinction between MSTM and Mie methods is observed at approximately 800 cm-1 (Figure 1). Here the MSTM method
computes much more realistic emissivity spectra than
the Mie method for all three radiative transfer models.
Among the three radiative transfer models, Conel
(1969) and Hapke (1996) models perform the best.
Moreover, these two models produce almost exactly the
same spectra. The Hapke (1993) does not perform as
well for this example, and this is likely due to the assumption in this model that heating takes place from
above which is not consistent with the conditions under
which laboratory emissivity spectra are acquired.
Overall, the MSTM method performed better than
Mie method, but there is still room for improvement.
The greatest mismatch between MSTM and laboratory
spectra occurred at wavenumbers above 1200 cm-1 and
below 300 cm-1. For these, the relatively small size of
the cluster of spheres may be interfering with the scattering process. Increasing the number of spheres could
allow better modeling capabilities for these two wavenumber regions.
Conclusions: This work demonstrated improved
models of emissivity spectra in the mid-infrared using
the MSTM light scattering method coupled with several
radiative transfer models. By comparing spectra from
the MSTM method to the Mie method and laboratory
spectra, the outstanding quality of MSTM method was
illustrated. However, MSTM is not perfect and more
improvements can be made to increase its performance.
Our next task is to do this, and in particular, reduce the
decrease in emissivity at high and low wavenumbers.
References: [1] Hunt G. R. and Logan L. M. (1972)
Appl. Opt., 90, 142–147. [2] J. W. Salisbury and Wald
A. (1992) Icarus, 96, 121–128. [3] Moersch J. E. and
Christensen P. R. (1995) JGR, 100, 7465–7477. [4]
Mustard J. F. and Hays, J. E. (1997) Icarus, 125, 145–
163. [5] Pitman K. M. et al. (2005) JGR, 110, E08003.
[6] Mishchenko M. I. et al. (1996) J. Quant. Spect. and
Radiative Transfer 55, 535–575. [7] Arnold J. A. et al.
(2012) LPS XLIII, Abstract #2529. [8] Glotch T. D. et
al. (2012) LPS XLIII, Abstract #2652. [9] Rucks M. and
Glotch T. D. (2014) AGU Fall Meeting, Abstract
#P23B-3987. [10] Donev et al. (2005) J. Comp. Phys.,
202, 737–764 (part I) and 765–793 (part II). [11]
Mackowski D. W. and Mishchenko M. L. (2011) J.
Quant. Spect and. Radiative. Transfer, 112, 2182–2192.
[12] Conel J. E. (1969) JGR, 74, 1614–1634. [13]
Hapke B. W. (1993) Cambridge Univ. Press, New
York. [14] Hapke B. W. (1996) JGR, 101, 16817–
16832.