1. Art and Diseño

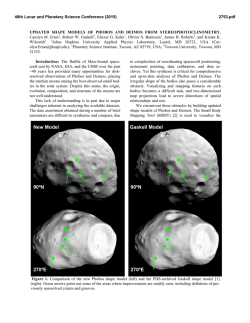
46th Lunar and Planetary Science Conference (2015)
1501.pdf
NUCLEAR SPECTROSCOPY OF IRREGULAR BODIES: COMPARISON OF VESTA AND PHOBOS.
T. H. Prettyman1 and J. S. Hendricks2, 1Planetary Science Institute (1700 East Fort Lowell, Suite 106, Tucson, AZ
85719, [email protected]), 2TechSource, Inc. (1475 Central Ave., Suite 250, PO Box 988, Los Alamos, NM 87544,
[email protected]).
Introduction: Gamma rays and neutrons are steadily produced by the interaction of galactic cosmic rays
(GCR) within the surfaces of airless planetary bodies.
Gamma rays are also made by the decay of long-lived,
radioelements K, Th, and U found in regolith materials.
The elemental composition of planetary regoliths, to
depths of a few decimeters, can be determined by analyzing emitted radiation measured from orbit or in situ.
Nuclear spectroscopy is effective within within about 1
body radius of planetary surfaces.
Nuclear spectrometers have been deployed on missions to the Moon, terrestrial planets, and asteroids Eros
and Vesta [e.g. 1]. Since the Moon and planets are are
round, with minimal topographic relief, corrections for
measurement geometry are often based on the first-order assumption that the flux of radiation arriving at the
detector varies in proportion to the solid angle subtended by a sphere with the same radius as the planet.
The assumption of solid-angle proportionality (ASAP)
is strictly valid, regardless of the shape of the planetary
body, when the flux of emitted radiation is isotropic
(e.g. for uncollided gamma rays made by the decay of
radioelements). For “smooth,” spherical bodies, observed departures from solid-angle proportionality may
result from anisotropic emission distributions for GCR
secondary radiation and, in the case of neutrons, loss
due to beta decay [2].
Vesta is the smallest body for which elemental composition has been mapped using nuclear methods. Vesta
has a triaxial shape with high relief in comparison to the
Moon, Mercury and Mars. For orbital mapping studies
using data acquired by NASA Dawn Mission’s Gamma
Ray and Neutron Detector (GRaND) [3], the flux of
gamma rays and neutrons was assumed to vary in proportion to the solid angle of Vesta, calculated at each
measurement location from a shape model [3,4]. The
validity of ASAP was verified empirically by examining the variation of counts with solid angle at high latitudes, which were well sampled in Dawn’s low altitude
mapping orbit [4-8]. Variations in solid angle were removed from the measurements to reveal Vesta’s surface
composition. Since the correction for solid angle was
by far the largest made to GRaND counting data, validation of ASAP is important in assessing sources of systematic error in mapped data.
For GCR-induced radiation, the relationship between measured counts and surface composition may
not be fully explained by the solid angle. For example,
it is easy to imagine that secondary radiation production
A
B
Fig. 1 Shape models of A) Vesta with 261-km mean volumetric radius (MVR) and B) Phobos with 11-km MVR.
by GCRs would be suppressed in shielded regions (e.g.,
within basins, canyons and craters) or that radiation
emission could be enhanced by scattering with topographic features such as basin walls. If so, then removal
of solid angle might introduce artifacts of shape and topography that could obscure variations in surface chemical composition.
Summary: In this study, we quantify the errors introduced by ASAP using detailed simulations of GCR
interactions with irregular bodies. For these simulations,
we modified the Monte Carlo radiation transport code
MCNPX [9] to treat complex shapes. Preliminary results indicate that spatial artifacts introduced by ASAP
are minimal for low-altitude measurements by Dawn at
Vesta: Corrections based upon MCNPX calculations do
not significantly change the results of previous mapping
studies. In contrast, ASAP breaks down over large altitude ranges, and artifacts of topography are observed
close proximity to Phobos. Improved correction methods are needed for missions proposed to small solar system bodies and for the analysis of low-altitude any data
set for which the instrument field-of-view is comparable
to topographic relief.
Modeling: MCNPX 2.7.5 was modified to include
a new surface type: a shape model specified by a triangle-vertex list. A voxel-based traversal algorithm was
used to speed-up intersections with surfaces containing
a large number of triangles, enabling fast simulations of
complex shapes. Shapes of Phobos and Vesta, determined by stereophotoclinometry, are represented by interconnected quadrilaterals (ICQs) [10, 11]. For our
study, the ICQ mesh was decimated and converted to
triangle-vertex format for ingestion into MCNPX. The
decimated models contained about 5×104 triangles (Fig.
1). MCNPX was also modified to treat neutron decay,
which can affect the flux of neutrons arriving at high
altitudes.
46th Lunar and Planetary Science Conference (2015)
GCR protons and alpha particles with energy distributions given by [12] were modeled. The gamma ray
and neutron leakage currents (energy-angle distribution) were tallied on concentric spheres spanning a
range of orbital altitudes. The spheres were subdivided
spatially into circular longitude and latitude regions using cones. For comparison, the average solid angle was
calculated for each longitude-latitude region. The composition of both bodies was assumed to be spatially uniform, with Vesta modeled as H-free howardite and Phobos as H-rich CM chondrite.
Results and Discussion: The total neutron leakage
current calculated by MCNPX is plotted against solid
angle and equivalent altitude (heq) in Fig. 2A for Vesta
(black) and Phobos (red). The points cluster into five
groups for corresponding to five concentric spheres on
which current was tallied (radii indicated on chart).
For Vesta, the radii span Dawn’s low altitude mapping orbit. For Phobos, tally spheres were selected to
represent a range of altitudes that could be sampled by
a future mission [e.g. 13]. The leakage current for Phobos is suppressed due to the presence of H in CM, which
moderates neutrons to low energies where they are preferentially absorbed. In both cases, current is strongly
correlated with solid angle; however, residuals (top
panel, Fig. 2A) show departures in linearity over the
wide range of altitudes sampled for Phobos.
If ASAP was valid, then maps of the ratio of neutron
current to solid angle should be featureless when composition is spatially uniform. Maps of this ratio are
shown for the innermost tally spheres in Fig. 2B&C.
Artifacts of relief (e.g. associated with the giant impact
basin Rheasilvia) are absent in Vesta’s ratio map. The
4% min-max variation in the ratio is small compared to
that of GRaND measurements with solid angle removed
(e.g. ~20% dynamic range for epithermal neutron
counts [4]). In comparison, the ratio map shown for
Phobos has higher contrast (~20%), which would bias
compositional maps determed using ASAP. The lowest
ratios are found in and around Stickney crater, which
also corresponds to the lowest sampled altitudes.
Improved methods: A model-based approach that
treats deviations from ASAP (e.g. caused by anisotropy,
shielding, and secondary scattering) is needed for closeup measurements of small, irregular bodies. MCNPX
provides a framework for investigating the these effects
and can be used directly to correct for shape and topography. A combination of MCNPX and simplified models [3] is used to characterize each of the aforementioned effects. For example, topographic shielding of
GCRs is not expected to be a large effect: GCRs with
low incidence angle, which would be blocked by basin
walls, contribute relatively little to radiation production
compared to those with normal incidence.
1501.pdf
A
Representative
uncertainty
Vesta
R2=0.998
420 km
445 km
470 km
495 km
520 km
Radii of tally spheres
14.5 km
17.1 km
Phobos
R2=0.993
19.8 km
22.4 km
25 km
B. Vesta
Ratio
1.02
Rheasilvia
1.00
0.98
C. Phobos
Ratio
1.06
0.97
Stickney
0.88
-180E
0
180E
Fig. 2. See Results and Discussion (left).
Acknowledgements: This work was funded by the
Dawn Mission under contract with NASA/JPL and by
NASA/NIAC grant NNX14AT50G.
References: [1] Prettyman T. H. (2014), in Encyclopedia of the Solar System ISBN:9780124158450.
[2] Maurice S. et al. (2004) JGR, 109, E7. [3] Prettyman
T.H. et al. (2011), Space Sci. Rev., 163, 371-459.
[4] Prettyman T.H. et al. (2012) Science, 338(6104),
242-246. [5] Lawrence D.J. et al. (2013), MAPS, 22712288. [6] Prettyman et al. (2013), MAPS, 48, 22112236. [7] Peplowski P.N. et al. (2013), MAPS, 48, 22522270. [8] Yamashita et al. (2013), MAPS, 48, 22372251. [9] Pelowitz, D.B., Ed. (2011), LA-CP-11-00438.
[10] Gaskell, R.W. priv. comm. [11] Gaskell, R.W.,
Gaskell Phobos Shape Model V1.0. VO1-SAVISA/VISB-5-PHOBOSSHAPE-V1.0. NASA/PDS,
2011. [12] O’Neill P. M. (2010), IEEE TNS, 57(6),
3148-3152. [13] Raymond, C. A. et al. (2015), AstroRecon, Abstract #6029.