1 Department of Mathematics MAL 100: Calculus Tutorial Sheet 2
1
2014-2015:Semester-II
Department of Mathematics
MAL 100: Calculus
Tutorial Sheet 2: Limits, Continuity and Differentiability
1. Discuss the following limits. If the limit exists and finite, find the limit. If the limit
goes to infinity, Justify?
x2/3 + x−1
sin x
sin x
(b) lim 2/3
(c) lim
(d) lim x sin x
(a) lim
2
x→∞ x
x→∞ x
x→∞
x→∞ [x]
+ cos x
2. Determine the points and nature of discontinuity of the following functions:
√
1 x ∈ Q
1
cos x
x4 + 1
x tan x
(a)
− 3x (b)
(c)
(e) f (x) =
(d) 2
0 x 6∈ Q
x−2
x − π/2
x +1
1 + sin2 x
3. Find the asymptotes of the graph of
(a)
x2 − 3
2x − 4
(b)
x2 − 4
x−1
(c)
x3 + 1
x
4. Find the following limits and determine if the functions are continuous at the point.
π
(b) lim sec(y sec2 y − tan2 y − 1) (c) lim tan( cos(sin x1/3 ))
y→1
x→0
4
(a) lim sin(x − sin x)
x→π
5. Determine if the following equations admits solutions in the interval mentioned.
π
2x + 1
(a) x5 − 3x2 = −1, [0, 1] (b) sin2 x − 2 cos x = −1, [0, ] (c) sin x −
, [0, π]
2
x−2
6. Bisection Method for finding roots: Let f (x) be a continuous function on [a, b] such
that f (a)f (b) < 0. Then show that f has a zero in [a, b]. Begin with a1 = a, b1 = b
1
and x1 = a1 +b
. If f (x1 ) = 0, we are done. Otherwise, apply the method on (x1 , b1 ) or
2
2
(a1 , x1 ). Define x2 = a2 +b
....and so on..Show that {xn } converges.
2
7. Determine which of the following functions are uniformly continuous in the interval
mentioned.
2
(a) ex sin(x2 ), (0, 1) (b) | sin x|, [0, ∞) (c)
√
x sin x
8. Determine
if the following functionsare differentiable at 0. Find f 0 (0) if exists
e− x12 x 6= 0
x cos 1 x 6= 0
x
(a)
(b) e−|x| (c)
0
0
x=0
x=0
9. Determine
if f 0 is continuousat 0 for the following
functions:
1
1
x3 sin 1 x =
2
6 0
x cos x x 6= 0
x2 ln |x|
x 6= 0
x
(a)
(b)
(c)
0
0
0
x=0
x=0
x=0
2
http://web.iitd.ac.in/∼sreenadh
10. When a circular plate of metal is heated in an oven, its radius increases at the rate of
0.01cm/min. At what rate the plate’s area increasing when the radius is 50 cm?
11. Show the following inequalities:
(a) for 0 < p < 1 and a, b ≥ 0, (a + b)p ≤ ap + bp .
(b) for p > 1, and a, b ≥ 0, (a + b)p ≤ 2p−1 (ap + bp ).
12. Let f be differentiable on IR and sup |f 0 (x)| < 1. Select s0 ∈ IR and define sn = f (sn−1 ).
IR
Prove that {sn } is a convergent sequence.
0
13. Let f be a thrice differentiable
function on (a, b) such that f (p) = 0, f (p) 6= 0 for some
f (x)f 00 (x) < 1. The following sequences come from the recursion
p ∈ (a, b) and sup 0 (x)2 f
(a,b)
formula for Newton’s method:
xn+1 = xn −
f (xn )
f 0 (xn )
Show that the sequence {xn } converges. In each case, begin by identifying the function
f that generates the sequence and determine if the sequence converges: x0 = 1,
(a) xn+1 = xn −
xn
1
+
2
xn
(b) xn+1 = xn − 1 (c) xn+1 = xn −
tan xn − 1
sec2 xn
14. Let f be differentiable on IR and |f (x)−f (y)| ≤ (x−y)2 . Then show that f is constant.
15. Prove that if f, g are differentiable on IR, f 0 (x) ≤ g 0 (x) on IR and f (0) = g(0), then
f (x) ≤ g(x) for x ≥ 0.
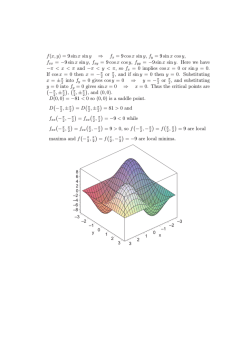
16. Find the first 3 terms of the Taylor’s expansion about the point x0 given
2
(a) sin x, x0 = π/2 (b) e−1/x , x0 = 0 (c) tan−1 x, x0 = 0
17. Show that Rn (x) → 0 as n → ∞ for the following functions
(i) log(1 + x) (ii) sinh x (iii) cosh x (iv) ax
(v) (1 + x)m , 0 < m ∈ Q, x ∈ (0, 1)
18. Find the domain of validity when sin x is approximated by x − (x3 /6) with an error of
magnitude no greater than 5 × 10−4
19. Estimate the error in the approximation of sin hx = x + (x3 /3!) when |x| < 0.5.
√
20. Find the error while approximating 1 + x with 1 + (x/2) in |x| < 0.01.
© Copyright 2026