1. Ingeniería

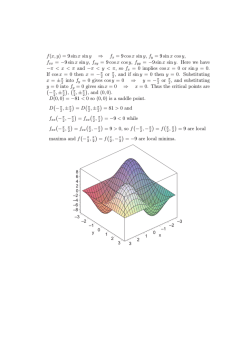
Crystallite size vs grain size
• Not equal, a grain can contain several
crystallites
Infinite crystal
• Electron density can be described to be
proportional to (r-rpqr).
• Scattering amplitude is then proportional
to (q-r*hkl).
One dimensional
1
Shape of the crystallites
• The electron density of a crystallite can be
presented as a product of the lattice term
(r) of the infinitely large crystal and the
shape function (r) of the crystallite.
• ( r)= (r)·( r)
(r)=1 inside the crystallite and 0 outside.
Amplitude F of crystallite
• F(q) =
(r) (r) exp(i q·r) d3r
• Using convolution theorem of Fourier
transform: F(q) = F (q)* (q). The star *
denotes convolution.
• The function (q) =
(r) exp(i q·r) d3r
• Intensity I(q) = F*(q) F(q).
2
Convolution theorem
Consider functions of one variable f and g.
Their convolution is f*g(x) = f(u)g(x-u)du.
Fourier transform
F(f*g) = f*g(x)exp(-ikx) dx
= dx du f(u)g(x-u) exp(-ikx).
Change of variable x-u = y.
F(f*g)(k) = dy du f(u)g(y) exp(-ik(y+u))
= du f(u) exp(-iky) du g(y) exp(-iku)
= Ff(k)·Fg(k).
Intensity of small crystallite
Patterson function
P(r) =
(u) (u+r) (u) (u+r) d3u
= V
(u) (u+r)>,
where V is the volume limited by the shape
function.
3
Intensity
• I N/V F2 Z(q) * | (q)|2
• F2 unit cell structure factor
• Z(q) lattice term
• (q)|2 broadening due to limited size.
Integrated intensity
Z(q) = sin(½(N1-1)q·a) /sin(½ q·a)
sin(½(N2-1)q·b) /sin(½ q·b)
sin(½(N3-1)q·c) /sin(½ q·c)
Set N1=N2=N3=N.
The maximum intensity at a Bragg peak can
be shown to be equal to f2N2. The width of
the peak is aproximately proportional to
1/N. The integrated intensity (the area of
the peak) increases proportional to N.
4
Crystallite size
• Form factor of a sphere F(x) = 4/3 a3
3 (sin x –x cos x)/x3, where x = qa.
• Reflection spot in reciprocal space is
approximated as a sphere, radius dq.
• The width of F(x)2 gives the angular width
of the diffraction peak 2 dq/(cos q0)
• q0 = 2 , 2dq = 3.6/R
• Angular width d(2 ) = 0.57 /(R cos )
Crystallite size: simple approach
• Let m be the number of parallel
planes
• Let 1 present the highest angle
(1) and 2 the lowest angle (2)
one can go before getting
destructive interference.
• The path differences are (m+1)
and (m-1) .
• Destructive interference with
planes in the middle of the
crystallite with path differences
(m+1) /2 and (m-1) /2.
B
t=md
5
Crystallite size
We assume triangular shape for the diffraction
peak, FWHM = B = (2 1-2 2)/2= 1 2.
Path length differences between rays scattered
from the front and back planes of the crystallite
2 t sin 1 = (m+1)
2 t sin 2 = (m-1)
t(sin 1 - sin 2 ) =
2t cos(( 1 + 2)/2) sin ((
By approximating
one obtains 2t (
t = /B cos
1
1
+
2)/2)
1
2)/2
2)/2 cos
=
=
B
and sin
x
B =
B
The average size of crystallites
• Assume a powder sample of crystallites of the
same size N1=N2=N3=N.
• In a powder crystallites take all orientations.
Thus one may consider only one rocking
crystallite.
• Let qhkl be the reciprocal lattice vector for the
reflection hkl.
• Let the directions of the primary and diffracted
beams vary slightly. Name q’ = q + q and s’-s’0
= s-s0 s.
6
Scherrer equation
Approximate sin2(Nx)/ sin2x N2exp(-(Nx)2 )
The intensity
I sin2(Nq·a)/ sin2q·a sin2(Nq·b)/ sin2q·b sin2(Nq·c)/
sin2q·c
becomes
I IeF2N6 exp(-( 2) N2(( s·a)2+( s·b)2+( s·c)2),
since
sin2(qhkl+2 s/ )·Nq/2 = sin2 (hN+ sNa/ )·Nq/2 =
sin2
s·Na).
Setting a=b=c,
I IeF2N6 exp(-( 2) (Na)2 q)2)
Scherrer equation
It is easier to rock the q-vector than the
crystallite. The difference vector is denoted
by s = x+y+ , and s2 = (xsin )2+y2+( cos )2
The intensity at fixed departure is
proportional to the sum of all values x and
y. I IeF2N6 exp(-( 2)(Na)2
cos )2)
2
2
2
exp(-(
)(Na) (x- sin ) )dx exp(-( 2)
(Na)2y2)dy.
The intensity becomes proportional to
I K exp(-( 2)(Na)2
cos )2) , where K
is a constant. This function is a gaussian
and and its FWHM is obtained from 1/2 =
exp(-( 2)(Na)2
cos )2).
y
x
s’-s0
q
s’
s
The broadening of the peak B(2 ) is about 2 .
7
FWHM of Gaussian
•
•
•
•
f(x) = exp(-x2/b2)
FWHM in terms of b:
exp(-x2/b2)= ½ => x2 = ln 2 b2
FWHM = 2x = 2(ln2)1/2 b
Scherrer equation
• B(2 ) = 2(ln2/ )1/2 /Na cos .
• Set L = Na =>
Scherrer equation
B(2 ) = 0.94 /(L cos ),
where B is the FWHM of the reflection
• More details in Warren, X-ray diffraction,
chapter 13
8
Stokes and Wilson
• Let P(2 ) be the measured intensity of a
reflection.
• Broadening has been also described as
(2 ) = P(2 )d(2 )/max(P(2 ))
• B(2 ) = /(L cos )
Experimental determination
1. Subtraction of background
2. Determination of maximum intensity:
statistical accuracy must be quite good
3. Determination of the FWHM: the angular
(q-scale) step must be small enough
compared to the width of the peak
4. Instrumental broadening affects also the
width
9
Instrumental broadening
• Let g(x) be the measured curve.
• Instrumental broadening is presented as an
integral equation
g(x) = h(x,y) f(y) dy + n(x),
where f is the exact result, h the instrumental
function (kernel), and n statistical errors.
• If the effect of the instrument is the same in all
points, the integral equation is of convolution
type: g(x) = h(x-y) f(y) dy.
Special solution for this case
• Sometimes it can be assumed that both the
diffraction peak and the instrumental function
are Gaussians. For the FWHM of a convolution
of two Gaussians f and g holds: f*g2 = f2 + g2
• For some other setups the peaks might be
approximated as Lorenz (Cauchy) functions
1/(1+a2x2).
• Then f*g = f + g.
10
Convolution of Gaussians
• f(x) = exp(-x2/b2)
• FWHM in terms of b:
exp(-x2/b2)= ½ => x2 = ln 2 b2
• FWHM = 2x = 2(ln2)1/2 b
• g= exp(-x2/d2)
• f*g = constant exp(-y2/(b2+d2))
Effect of strain on diffraction peak
11
Broadening of reflection: strain
• No strain, the position of the peak q =
/d, where d is the distance of the lattice
planes
• Uniform strain: d increases => q
decreases.
• Non-unform strain: d varies: If <d>=d, the
position may not change, but the FWHM of
the peak increases.
Broadening
• Bragg law 2d sin =
• Differentiate 2 d sin + 2d cos
•
d/d tan = 2
=0
12
Size distribution for crystallites
• By fitting a simulated powder pattern,
derived from an appropriate physical
model, to experimental data.
• dislocations and other lattice distortions
• Model shapes for size distributions
– Gaussian G(x) = (2 b2)-1/2 exp(-(x-a)2 /2b2)
– Lognormal
f = 1/(r(2 ln(1+c))1/2
exp(ln(r/<r>(1+c)1/2)2/(2ln(1+c)));
Size-strain line broadening
For analysing line broadening, correction for
instrumental broadening must be done first.
– Wavelength dispersion
– Slits
Deconvolution, ill-posed problem: good
measurements are essential!
Voight function is usually assumed for the line
shape in the powder diffraction refinement
programs.
13
Broadening: size, strain
• Size (Scherrer): FWHM proportional to
1/cos
• Strain: FWHM proportional to tan
• Measure peaks, e.g. 00l.
• Determine the widths
• Plot the width as a function of l (or angle)
• Study the angular dependence.
Profile fitting
• Lorenzian (Cauchy function)
FWHM = A/cos + B tan + C
• Voight function
FWHM = U tan2 + V tan + W + P/cos2
14
Good references
• J. I. Langford, D. Louër and P. Scardi. Effect of a
crystallite size distribution on X-ray diffraction
line profiles and whole-powder-pattern fitting. J.
Appl. Cryst. (2000). 33, 964-974
• D. Balzar et al. Size-strain line-broadening
analysis of the caria round-robin sample. J. Appl.
Cryst. 2004, 37, 911-924.
• Ungar et al. Crystallite size distribution and
dislocation structure determined by diffraction
profile analysis: principles and practical
application to cubic and hexagonal crystals. J.
Appl. Cryst. 2001, 34, 298-310.
Diffraction pattern of wood
002
q=4
003
sin
q
-110
Reflection 004
110
Reflection 200
102
15
Monoclinic Cellulose I
004
C-axis
200
In-situ X-ray diffraction and tensile
testing
• Stress-strain curves from tensile testing give
information on the deformation of the
macroscopical sample
• X-ray diffraction (XRD) gives the the behaviour of
crystalline cellulose under tension.
16
Comparison of ESRF and HASYLAB
ID13 at ESRF, France
A2 at Hasylab, Germany
Undulator
Bending magnet
5 µm beam
250x 250 µm beam
0.96 Å (13 keV)
1.5 Å (8 keV)
stretching rate 0.2 µm/s,
meas. Time 21 s
stretching rate 0.2 µm/s,
measuring time <10 s
Beamline A2
Early wood, year ring 4, initial MFA 9º
• Reflection 004 moved to smaller
scattering angles: elongation of
cellulose chain (0.5%)
• Width increased: strain
• Intensity decreased: lattice distortions
004
ESRF
17
Warren-Averbach
• Profile of Bragg reflection P(q) is assumed as a
convolution of profiles presenting strain and size
distortion.
• P(dqi) = const A(l,dqi) cos(qL) + B(L,dqi) sin(Lq),
where L gives the distance perpendicular to the
diffracting planes and dq is the deviation from the
reflection position.
• Fourier transform of the profile gives for the Fourier
coefficients A(L) and B(L). Usually only A(L) are
considered.
• ln A(L) = ln ALs - 2 2 L2 g2 <e2>, where ALs are size
coefficients, g the absolute value of the scattering vector,
and <e2> is the mean square strain. The parameter L is
defined as L=na3, where a3 = (sin 2-sin 1), n integer.
Warren-Averbach
• To obtain information on size and distortion
coefficients, at least two orders of reflection have
to be measured.
• See e.g. Warren: X-ray diffraction, Berkum et al.
Applicabilities of the Warren-Averbach analysis
and an alternative analysis for separation of size
and strain broadening. J. Appl. Cryst. 1994, 27,
345-357.
18
XRD and elastic properties
•
•
•
•
1-d case, stretched cylinder
Force F in y-direction
Tension F/A
Increase of length y = L/L, where L
is the length of the cylinder.
• Hooke’s law F/A = E y, where E is
Young’s modulus and A the area of
the cross section of the cylinder.
• For a cylinder x= y = D/D = - y,
where D is the diameter and is the
Poisson ratio.
y
F
L
Elastic properties
• Determining relative increase of length
using x-rays. Determine change of lattice
spacing d/d of lattice planes
perpendicular to the force F.
• F/A = E/ d/d.
19
Residual stress
• When metal bar is deformed (applied
stress) it causes inner stress.
• Microstrain: Lattice planes are deformed, d
varies.
• Macrostrain: Distance of lattice planes
increases uniformly.
20