1. No category

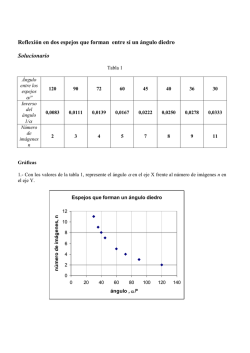
Guía Adicional Nº04) Movimiento Parabólico
Guía de Ejercicios
Adicionales
Nº04
FISICA NIVELACIÓN
Movimiento Parabólico.
SEGUNDO
SEMESTRE
2005
1) Demuestre las expresiones indicadas en las diapositivas 9, 10 y 11 del apunte de lanzamiento
de proyectiles.
2) Un pato volaba por una recta
horizontal a la velocidad
constante “u”. Un “cazador”
inexperto le lanzó una piedra,
con la particularidad de que el
lanzamiento fue hecho sin
corrección del avance, es
decir, en el momento del
lanzamiento la dirección de la
velocidad de la piedra (el
ángulo α respecto al horizonte) esta orientada precisamente hacia el pato como muestra la
figura. Si el módulo de la velocidad inicial de la piedra es “v”, ¿A qué altura volaba el pato si la
piedra, a pesar de todo, dio con él?
3) Se apunta un rifle horizontalmente a través de su mira hacia el centro de un blanco grande que
está a 200 [m]. La velocidad de la bala es de 500 [m/s].
a) ¿A qué distancia vertical del centro del blanco golpea la bala?
b) Determine el ángulo de elevación con respecto a la línea de puntería con que se debería lanzar
la bala para que dé justo en el centro del blanco,
4) Desde el punto A de una banda
transportadora se descarga arena sobre
una tolva como muestra la figura. ¿Entre
qué límites de velocidad de la banda
caerá la arena dentro de la tolva BC?
5) En ocasión de las Olimpíadas de 1968
en la Ciudad de México, Bob Beamon
(USA) rompió el record de salto largo con un salto de 8,90 [m]. Suponga que su velocidad inicial en
el punto de separación del suelo era 9,50 [m/s], casi igual a la de un corredor veloz. ¿Qué tan cerca
estuvo este atleta de primera clase de llegar al alcance máximo posible en ausencia de una
resistencia de aire?. El valor de g en la Ciudad de México es de 9,78 [m/s2].
6) Un proyectil es disparado desde la
superficie a nivel del terreno con un
ángulo φ0 arriba de la horizontal, como
muestra la figura:
(a) Pruebe que la razón de la altura
máxima H y el alcance R está dada
H 1
= tg (φ0 ) .
por
R 4
(b) Halle el ángulo de proyección para
el cual la altura máxima y el alcance
horizontal son iguales.
(c) Demuestre que el ángulo de elevación θ del punto más elevado tal como se le ve desde el punto
1
de disparo se relaciona con φ0 según tg (θ ) = tg (φ0 ) . Calcule θ para φ0 = 45º.
2
200 [m]
VB = 500 [m/s]
Física Nivelación 2005