1. No category

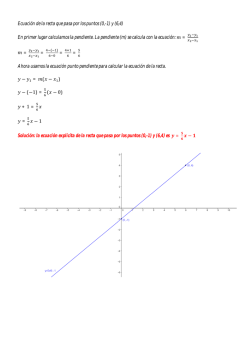
Hagamos un diagnostico y veamos
cuanto hemos aprendido!!!
Profa. Ysela Ochoa Tapia
REPASO PARA EL SEGUNDO PARCIAL (MATE3171)ISEM14-15
3+ 2x
1) El dominio y el rango de
3) Encuentre el dominio de:
2) El dominio de f (x ) =
2 − 5x
x
f (x ) = 2x − 3 es:
f (x ) = 2
es:
2x + x −1
4) Si h(t) = 4t −
1
entonces h(t +1) es:
t2
5) Grafique: f (x ) = x + x
1.3 PENDIENTES, RECTAS Y FUNCIONES LINEALES
1) Los interceptos de y 2 = −12x + 36
2) Hallar la pendiente de una recta que pasa
por P(2,-1) y Q(0,3)
3) ¿Cuáles de los puntos P(1,2), Q(4,4),
4) Use las pendientes para determinar si los
R(7,6) y S(9,7) están en una misma recta?
puntos A(-1,3) , B(1,7) y C(4, 15) son
colineales.
5) Si M(6,8) es el punto medio del segmento
6) Encuentre la ecuación de la recta que pasa
AB y A tiene coordenadas (2,3), encuentre
las coordenadas de B.
por el punto medio entre A(1,4) y B(7,-2) y
que es perpendicular al segmento AB.
7) Halle la ecuación de la recta perpendicular
a 2y − x = 3 que pasa por (2,5).
8) Una ecuación para la recta paralela a la
gráfica de x −y = 5 , con intercepto y = 2.
9) La ecuación de la recta con pendiente 2/5
10) Una recta vertical que pasa por (5,3)
e intercepto en y = 1 es:
tiene ecuación:
11) Halle la ecuación de la recta que pasa por
el origen y que es paralela a la recta que pasa
por los puntos
(1,2) y (9,-1).
1.4 RAZON DE CAMBIO PROMEDIO
1) Sea f (x ) = 1− 3x Halle la razón de cambio
promedio de f en el intervalo a ≤ x ≤ a +h .
2) Sea f (x) =
3) Dada la función f (x ) = 4 − x 2 .Determine la
4) La altura de un cohete que se tiró
razón de cambio para x = 1 y x = 1+ h .
directamente hacia arriba está dada por
2
. Halle la razón de cambio
x
promedio de f en el intervalo. [x, x +h ]
s(t) = 80t − 9.8t 2
Determina la razón de cambio para t = 2 y
t = 5 segundos.
1.5 FUNCIONES DEFINIDAS POR PARTES
$2x
#x
si x ≤ −3
&
%
si -3 < x < 1
1) Sea f (x ) = %−1
2) Sea f (x ) = $3− 2x
& 2
%−3
'x − 2 si x ≥ 1
&
a) f (−4)
b) f (0)
c) f (1)
Graficar
si
-2 ≤ x < 1
si
si
1≤x ≤3
x >3
Graficar y encontrar el Dominio y el Rango.
3) Dibuje la grafica de:
#4 − x
si x < 0
%
f (x ) = $2x + 4 si
0 ≤ x ≤1
%5x +1
si
x >1
&
4) Dibuje la gráfica de:
#2x + 3
si x < −1
f (x ) = $
si
x ≥ −1
%3− x
5)Escriba una formula para la función lineal
6) Dada la gráfica:
por partes con la gráfica a continuación:
11
3
a) Encuentre el dominio y rango.
2
4
6
8
b) El valor de f(4) es:
c) Un intervalo en donde la grafica es
creciente:
d)¿Para cuántos valores de x es f(x) =-1
7) Considere la ecuación y = 2x + 3 !
8) Considere la ecuación y = 6 − 3x !
a) Dibuje la gráfica.
b) Encuentre los interceptos en x y y.
a) Dibuje la gráfica.
b) Encuentre los interceptos en x y y.
#3x −1
9) Si f (x ) = $
%x + 2
si
si
x≤4
entonces
x>4
g(4) es:
10) Evalúe:
"x 2
si
f (x ) = #
$x +1 si
x <0
x ≥0
a) f (−2)
b) f (0)
c) f (1)
1.6 FUNCIONES DE POTENCIA
1) ¿Qué función representa la gráfica?
a)
b)
c)
d)
2) W es directamente proporcional a t y w =
5 cuando t = 8; entonces la constante de
3) Si t es inversamente proporcional a r y
r = 3 cuando t = 12, entonces t = ?
proporcionalidad es:
4) El volumen V de una esfera es
5) El peso de un cilindro (en kilogramos) es
directamente proporcional al cubo de su
directamente proporcional al cuadrado de su
4 3
π r . ¿Cuál es la constante
3
de proporcionalidad?
circunferencia C. Utilice los datos dados en la
siguiente tabla para encontrar el peso de una
cilindro con una circunferencia de 150
centímetros.
radio r. Si V (r ) =
C
w
50
30
100
120
1.7 ARITMETICA Y COMPOSICION DE FUNCIONES
1) Dado f (x ) = 4 − x 2 , g(x ) = 1+ x
encuentre f + g y f / g indicando sus
dominios.
2) Para f (x ) = 2 x y g(x ) = 1− 2 x encuentre
y simplifique las formulas para: f + g , f − g ,
f •g y f / g indicando sus dominios.
3) Sean f (x ) = 3x 2 −12 y g(x ) = 7 − x . Evalué
cada una de las siguientes:
4) Sean f (x ) = x y g(x ) =
de las siguientes:
a) f (g(2))
1
. Evalué cada una
x
a) f (g(4))
b) g(f (−1))
b) ( f ⋅ f ) (2)
c) f (f (2))
1
c) g(f ( ))
16
d) g(g(2))
5) Las tablas a continuación representan las
funciones de f y g respectivamente. Haga
tablas para representar las composiciones
f !g y g ! f .
x
1
2
3
4
5
f(x)
2
3
5
1
4
x
1
3
2
3
4
5
2
4
5
1
g(x)
6) Dada la función f encuentre funciones g y
h (diferentes de f ) tal que f = g !h .
1
f (x ) =
(x +1)2
7) Para cada una de las funciones siguientes encuentre y simplifique f ! g y g ! f .
x +2
a) f (x ) = x y g(x ) = x 2 +1
b) f (x ) = 2x +1 y g(x ) =
2
8) Sean f (x ) = x 2 y g(x ) = x −1 .
a) Encuentre (g ! f )(x ) y (f ! g)(x )
b) Dominio y Rango respectivo.
10) Sean f (x ) = 2 − x ; g(x ) = x
a) Encuentre (g ! f )(x ) y (f ! g)(x )
b) Dominio y Rango respectivo.
x
x −1
a) Encuentre (g ! f )(x ) y (f ! g)(x ) .
9) Sean f (x ) = x 2 ; g(x ) =
b) Dominio y Rango respectivo.
11) Sea f (x ) =
a) (f ! g)(x ) =
b) (g ! f )(x ) =
c) (f ! g)(1) =
12) Sea f (x ) = 3x 5 − 5 y g(x ) = 2x + 3
a) f (g(1)) =
b) f (x ) − g(x ) =
2
y g(x ) = x 2 + 3
x
1.8 FUNCIONES INVERSAS
1) La función que corresponde a la regla:
“Multiplicar un número por cuatro y restarle
2” es: ¿Cuál es la función inversa?
2) Encuentre si es posible la función inversa
de f dada por la tabla.
x
f(x)
3) Determinar si f (x ) = 3x − 2 , g(x ) = x 2 − 2x
es uno a uno.
5) Sea f (x ) = 5x − 4
a) f −1 (x )
b) f (0)
c) f (2)
0
5
1
4
2
3
3
2
4
1
5
5
4) ¿Cuál de las siguientes graficas es una
función uno a uno?
a)
b)
c)
d)
6) Sea h(x ) = 5 − 3x entonces h(h −1 (2)) =
d) Graficar f y f −1
7) Utilice composición de funciones para demostrar cuál de los siguientes pares de funciones
son inversas entre sí:
a) f (x ) = 3 3x − 4
b) g(x ) =
(x 5 + 4)
3
8) Encuentre la función inversa de cada una de las siguientes funciones:
x +1
2x −1
a) f (x ) =
b) f (x ) =
2x − 3
x −4
Además encuentre el dominio y rango de la
función inversa de f
Además encuentre el dominio y rango de la
función inversa de f
c) g(x ) = x 2 − 2x + 5 , x > 1 . (Sugerencia: complete el cuadrado)!