1. Healthcare

COLEGIO COLOMBO BRITÁNICO
“Formación en la Libertad y para la Libertad”
MATEMÁTICAS
GRADO:7O
DOCENTE: Nubia E. Niño C.
FECHA: 2 / 02 / 15
TALLER: # 1 – 2 y 1 - 3
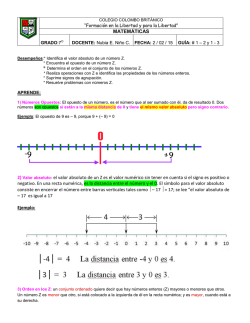
Desempeños:* Identifica el valor absoluto de un número Z.
* Encuentra el opuesto de un número Z.
* Determina el orden en el conjunto de los números Z.
* Realiza operaciones con Z e identifica las propiedades de los números enteros.
* Suprime signos de agrupación.
* Resuelve problemas con números Z.
NOTA  Todo el taller se desarrolla en el cuaderno; mostrar proceso y dar la (s) respuesta (s) claramente.
ACTIVIDADES:
1) Leer, analizar y resolver los siguientes problemas:
a) Un buceador está sumergido a – 24 metros del nivel del mar y sube a una velocidad de 3 metros por minuto. ¿A qué
profundidad estará al cabo de 5 minutos?
b) El llave de una bañera está estropeada y pierde 2 litros de agua cada día. Cuando la arreglaron había perdido 24
litros. ¿Cuántos días estuvo estropeada?
c) Guillermo se baja del ascensor en la 4ª planta y se sienta a esperar su turno para el dentista. Observa como
el ascensor sube 3 pisos, luego baja 8, más tarde sube 3, luego sube 5 más, para después bajar 5 y luego
bajar 2 más. ¿En qué planta se ha detenido finalmente? Si en pasar de un piso al siguiente tarda 5 segundos,
¿cuánto tiempo ha estado en funcionamiento para hacer el recorrido que ha observado
Guillermo?
d) En un depósito hay 800 litros de agua. Por la parte superior un tubo vierte en el depósito 25 litros por minuto, y
por la parte inferior por otro tubo salen 30 litros por minuto. ¿Cuántos litros de agua habrá en el depósito después
de 15 minutos de funcionamiento?
e) Un día de invierno amaneció a 3 grados bajo cero. A las doce del mediodía la temperatura había subido 8 grados,
y hasta las cuatro de la tarde subió 2 grados más. Desde las cuatro hasta las doce de la noche bajó 4 grados, y
desde las doce a las 6 de la mañana bajó 5 grados más. ¿Qué temperatura hacía a esa hora?
f) Un gusano sube por una pared lisa. Si por cada 3 cm que avanza se desliza 2 cm, ¿al cabo de cuántos intentos
logra trepar 5 cm?
g) Un submarino está a 210 metros bajo el nivel del mar. Debido a las fuertes corrientes tiene que descender
74metros. Más tarde decide subir 50 metros. ¿A qué profundidad está el submarino?
h) En una cinta de vídeo has grabado dos documentales de 15 minutos y tres vídeos musicales de 5 minutos.
Después borras uno de los documentales. ¿Cuántos minutos hay grabados después de borrar el documental?
i) El nivel del agua de una represa ha disminuido 8 cm diarios durante 6 días. A causa de las intensas lluvias caídas
los 3 días siguientes ha subido el nivel 7 cm diarios. ¿Cuál ha sido el desnivel total del agua de la represa?
2) Escribir el nombre de la propiedad que representa cada una de las igualdades.
a)
b)
c)
d)
7 + (– 3) = (– 3) +(7)
(– 8) + 0 = (– 8)
18 + (– 18) = 0
[7 + (– 3)]+ (– 5) = 7 + [(– 3) + (– 5)]
3) Responde:
a) ¿Qué número sumado con – 50 da 28?
b) ¿Qué número se le debe restar a – 42 para que la diferencia sea – 100?
c) ¿Cuál es el número que sumado con 0 da – 35?
Si el sustraendo es 3 y la diferencia –11 ¿cuál es el minuendo?
Si el primer sumando es – 5 y la suma – 13 ¿cuál es el otro sumando?
¿Qué significa que la adición o suma en el conjunto Z, verifica la propiedad clausurativa?
Dados los sumandos +10 y – 35, escribe la adición teniendo en cuenta la propiedad conmutativa y halla la
suma.
h) ¿Es siempre la diferencia de dos números enteros otro número entero?
i) ¿Son iguales los resultados que obtienes al restar 3 de 5 que 5 de 3?
j) El resultado que obtienes de la operación (5 – 3) – (– 2) es el mismo que obtienes al resolver 5 – (3 – (– 2))?
¿Qué puedes deducir de esta observación.
k) ¿Existe un elemento neutro para la resta en Z?
d)
e)
f)
g)
4) Completar el siguiente cuadro:
a–b+c–d
Valores
a
b
c
d
7
3
–9
– 11
–4
–8
+5
17
– 21
+3
1
– 12
(– a) + b – (– c) + (– d)
5) Representar las siguientes operaciones en la recta numérica, hacer una para cada caso:
a) 4 + (– 3) – 6 =
c) (– 8) + 3 – 2=
b) (– 5) + (– 3) + 7 =
d) (– 3) + (– 4) + 9 =
6) Al resolver la siguiente expresión: – b + {a + [– c + (a + c – b)] – [– b + (a – b – c)] – c} teniendo en cuenta que:
= – 2, b = 3, c = – 1, el resultado es:
7) Resolver los siguientes polinomios:
O
5
a) – 16 + 9 + {9 – 4 – 2 [1 +
b) √81 –
√32 (– 8  3 + 6O) + 23 – 5 + (- 3 – 5  7 + 2]} =
4
√16 + 5O {– 22 – [16 – 32 + (– √9 + 7 – 14 + 70) + 2 (8  4)]} =
3
√− 27 + 32 – 18 {– 19 + [– √36 + 3O (8 – 29 – 2) + (7 – 4  2)]} =
c) –
d) –
5
3
√8 + 7 – 3 {8 – 13 – [1 (11 + 4 – 3  8) + 21 – 35 + 3 O (17 – 18 – 5) + 7]} =
e) – 4 – √16 – {8 + 1 [4 – (7 – 13 + 4  (– 3)) – 11 + 1 (
2
0
f) – √25 + 3 – 4 + 1 {– 2 + [–
2
g) –
4
2
7
√36 – 18)] – 7 + 2} =
√25 + 6O (9 – 24 + 3) + (– 7 + 4 – 11 + 2)]} =
3
√81 + 6O {– 13 – [5 – 4 + (– 8 + 22 – √− 125 ) + 22 (– 9 + 11 – 91)]} =
8) Escribir V, si la expresión es verdadera o F, si es falsa. Justificar cada respuesta.
a) El producto de todo número Z por cero da como resultado el mismo número.
b) En el desarrollo de los polinomios no es necesario tener en cuenta el orden de las operaciones.
c) El producto entre dos Z de igual signo es negativo.
d) El producto de cuatro Z algunas veces es positivo.
e) Polinomio aritmético es: una expresión matemática en la que se encuentran indicadas varias operaciones
matemáticas que no pueden tener signos de agrupación.
a
f) Para eliminar signos de agrupación en un polinomio aritmético, se elimina cada signo de agrupación de afuera hacia
adentro.
g) La diferencia de los núm eros enteros se obtiene restando al m inuendo el opuesto del s ustraendo
h) La ley de signos s e aplica en la sum a y en la resta de núm eros Z.
9) Aplicar la propiedad distributiva en los siguientes ejercicios:
a) 5 x (3 – 1 + 4) =
b) 9 x (7 + 3 – 2) =
c) (5 – 2 + 6) x 8 =
d) (8 + 4 – 5 – 2) x 7 =
e) (5 – 9 + 6 – 2) x 6 =
10) Resolver y completar la siguiente tabla:
a
b
c
–3
–2
–1
2
3
–4
2
–1
–5
–4
2
–6
–1
7
–2
abc
b  (a + c)
a  c (– 1)
11) Justificar cada situación dando un ejemplo:
a) Si multiplicas 2 números enteros que no tienen el mismo signo, ¿el resultado será un número entero positivo o uno
negativo?
b) Si multiplicas 2 números enteros negativos, ¿el resultado será un número entero negativo o positivo?
c) Si multiplicas 2 números enteros, ambos positivos ¿el resultado será un número entero positivo o negativo?
12) Con los siguientes datos  8 + 11 + 9 +3 + 5 aplicar las propiedades que se indican para cada caso a la vez:
a) asociativa y conmutativa
b) modulativa, asociativa y conmutativa
c) modulativa y asociativa
13) Ordenar, en sentido decreciente, representar gráficamente, y calcular los opuestos y valores
absolutos de los siguientes números enteros:
8, −6, −3, 3, −2, 4, −4, 0, 7 , 1
14) Determinar el opuesto de cada número Z:
A) – (– 19)
B) – (61)
C) – 8
D) – (– (– 37))
E) 43
F) – (– 25)
G) – (– (– 126))
15) Indicar los números Z que están representados por las letras en la recta:
A


B



C




D




1



E

 
F
H
      
16) Representar en la recta numérica los 8 primeros números enteros cuyo valor absoluto es menor que 6.
17) Representa en la recta numérica todos los números cuyo valor absoluto es:
a) Igual a 4.
b) Menor o igual que 5.
c) Igual a 0.
18) En cada numeral escribir los números enteros que cumplen la condición que se indica:
a)
b)
c)
Su valor absoluto es 17.
Son mayores que – 7 y menores que + 2.
Su valor absoluto es menor que 3.
19) ¿Hay algún número que coincida el número, su opuesto y su valor absoluto?; si la respuesta es verdadera, ¿cuál es
el número?
20) ¿Cuál de las siguientes igualdades es falsa; sustentar la respuesta:
a) |–18| = – 18
b) |– (– 23) | = – 23
c) | 46| =+ 46
e) | a| = – 9
21) Calcular los siguientes valores absolutos:
a) – – 9 + 10 – 7 +– (3 – 8 + 5)
2
c)
0
– 3 – 3 + 5  – – 4 (5 – 18  3)
0
2
b) – 2– 9 + 5  – – (– 3 – 8  2)=
=
=
d) – 2 + 3 +– 11 + 7 + – (8 – 14  2)=
22) Determinar el punto opuesto a cada uno de los puntos localizados en el plano cartesiano.
23) Ordenar las siguientes temperaturas en orden ascendente: – 5 °C, 0 °C, +3 °C, –9 °C, +7 °C, – 13 °C, +7 °C,
21) Llena los espacios con la palabra, frase o afirmación correcta.
a. Los enteros positivos son_________________
b. Los enteros negativos son__________________
c. El entero a es menor que el entero b (a < b), si a está a la _____________de b en la recta numérica.
d. b es mayor que a se escribe___________
e. El inverso aditivo de a es _____
f. El valor absoluto de un número n es su _____________ de 0
g. ¿El conjunto Z, es un conjunto finito o infinito? ¿Por qué?
h. ¿N  Z? ¿Por qué?
22) Responde:
a. Si x
= 5, ¿Cuál es el valor de x? Tendrá un solo valor?
b.
c.
d.
e.
f.
Si w = 5, ¿Cuál es el valor o valores de w?
17. Si -7 = m, ¿Cuál es el valor de m?
18. Si 8 = t, ¿Cuál es el valor de t?
19. Si n = 8, ¿Existe algún valor que satisfaga n?
20. Si 0 = n, ¿Cuál es el valor de n?
Fuentes Bibliográficas:
 Joya Vega, Anneris. Nuevas matemáticas. Editorial Santillana 2008
 recursostic.educacion.es
 Nubia Esmeralda Niño Cárdenas
 www.thatquiz.org/es
 masmatematicaparavos.blogspot.com
 http://sites.google.com/site/areamatlaens
 http://www.vitutor.com/
 www.tareasplus.com
 www.juntadeandalucia.es
 nea.educastur.princast.es
 www.denumeros.com
 http://www.rinconmaestro.es/
 http://www.curriculumenlineamineduc.cl/
 Imágenes de: spanishged365.com
Nubia Esmeralda Niño Cárdenas
“De naDa sirve correr; lo que conviene es partir a tiempo”
La Fontain