1. Healthcare

COLEGIO COLOMBO BRITÁNICO
“Formación en la Libertad y para la Libertad”
MATEMÁTICAS
GRADO:7O
DOCENTE: Nubia E. Niño C. FECHA: 2 / 02 / 15
GUÍA: # 1 – 2 y 1 - 3
Desempeños:* Identifica el valor absoluto de un número Z.
* Encuentra el opuesto de un número Z.
* Determina el orden en el conjunto de los números Z.
* Realiza operaciones con Z e identifica las propiedades de los números enteros.
* Suprime signos de agrupación.
* Resuelve problemas con números Z.
APRENDE:
1) Números Opuestos: El opuesto de un número, es el número que al ser sumado con él, da de resultado 0. Dos
números son opuestos si están a la misma distancia de 0 y tiene el mismo valor absoluto pero signo contrario.
Ejemplo: El opuesto de 9 es – 9, porque 9 + (– 9) = 0
2) Valor absoluto: el valor absoluto de un Z es el valor numérico sin tener en cuenta si el signo es positivo o
negativo. En una recta numérica, es la distancia entre el número y el 0. El símbolo para el valor absoluto
consiste en encerrar el número entre barras verticales tales como – 17 = 17; se lee “el valor absoluto de
– 17 es igual a 17
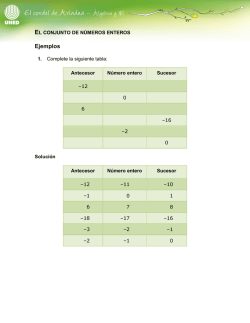
Ejemplo:
3) Orden en los Z: un conjunto ordenado quiere decir que hay números enteros (Z) mayores o menores que otros.
Un número Z es menor que otro, si está colocado a la izquierda de él en la recta numérica; y es mayor, cuando está a
su derecha.
Relaciones de orden en los Z: El orden en los enteros satisface las siguientes relaciones:
ab
ab
a=b
mayor
2–4
menor
–13
igual
5=5
Criterios para ordenar los Z: 1) Todo número negativo es menor que cero.  – 18  0
2) De los enteros positivos, es mayor el que tiene mayor valor absoluto.  9  15
3) Todo número positivo es mayor que cero.  5  0
4) De dos enteros negativos es mayor el que tiene menor valor absoluto.  – 6  – 21
Operaciones en Z:
A) Suma de números enteros: a) Si los números enteros (Z) tienen el mismo signo , se suman los
valores abs olutos y al resultado se le coloca el signo com ún .
Ejemplos: 17 + 3 + 5 = 25
(– 17) + (– 3) + (– 5) = – 25
– 3 + (– 5) = – 8
b) Si los núm eros enteros (Z) son de distinto s igno , se restan los valores absolutos (al m ayor le
restam os el m enor) y al resultado se le coloca el signo del número de mayor valor absoluto .
Ejemplos: – 19 + 8 = – 11
19 + (– 8) = 11
B) Propiedades de la suma de números enteros :
a) Clausurativa: la suma de números enteros es siempre otro número Z.
Ejemplo: Si a y b  Z
a+bZ
21 y (– 13)  Z; 21 + (–13) = 8
b) Asociativa: al agrupar los sumandos de diferente forma, siempre da el mismo resultado.
Ejemplo: ( a + b) + c = a + ( b + c)
(2 + 3) + ( − 5) = 2 + [3 + (− 5)]
5 − 5 = 2 + (− 2)
0=0
c) Conmutativa: el or den de los sum andos, no altera el res ultado.
Ejemplo: a + b = b + a
18 + (– 8) = (– 8) + 18
10 = 10
d) Elemento neutro : La sum a de cualquier núm ero Z con 0, da com o resultado el m ism o núm ero Z
Ejemplo: a + 0 = a 75 + 0 = 75; ( – 85) + 0 = – 85
e) Inverso aditivo o elemento opuesto : todo núm ero Z sum ado con su opuesto, da com o
resultado = 0
Ejemplo: a + (– a) = 0  23 + (– 23) = 0
C) Resta de números enteros : La diferencia de los números enteros se obtiene s um ando
al m inuendo el opuesto del sustraendo.
Ejemplo: a - b = a + (- b)  17 – 31 = – 14
17 + (– 31) = – 14
D) Supresión de signos de agrupación : Los signos ( ) (paréntesis),   (corchetes) y { } (llaves) son
llamados signos de agrupación y su papel, es agrupar operaciones.
Para eliminar o suprimir signos de agrupación tenemos las siguientes reglas:
Saber que los signos los eliminaremos de adentro hacia afuera.
Si el signo de agrupación esta precedido del signo más (+) se deja el mismo signo a todas las cantidades que se
hallen dentro de él.
Si el signo esta precedido del signo menos (–) se le cambia el signo a todas las cantidades que hallen dentro de él.
Ejemplo: 17 - {6 + 3 - [-7 + 3 + (- 3 + 8 – 5) + 6 -1] + 6} + 3 =
17 - {6 + 3 - [-7 + 3 - 3 + 8 – 5 + 6 -1] + 6} + 3 =
17 - {6 + 3 +7 - 3 + 3 – 8 + 5 - 6 + 1 + 6} + 3 =
17 - 6 - 3 -7 + 3 - 3 + 8 - 5 + 6 - 1 - 6 + 3 = 37 – 31 = 6
E) M ultiplicación de números enteros :
Para multiplicar dos números enteros se multiplican sus valores absolutos; si los dos factores
tienen igual signo, el producto es positivo, y si los dos factores tienen distinto signo, el
producto es negativo; Se debe tener en cuenta la aplicación de la ley de los signos .
ley de signos:
+
−
+
−
·
·
·
·
+
−
−
+
=
=
=
=
+
+
−
−
Ejemplos:
a) 2
·
5 = 10
b) (−2)
c) 2
·
·
(−5) = 10
(−5) = −10
d) (−2)
·
5 = −10
Para multiplicar tres o más números enteros, a) se multiplican dos y el resultado se multiplica por otro y así
sucesivamente hasta multiplicar por todos los factores (el producto tiene la propiedad asociativa, da igual el orden en
que se multipliquen los factores), b) o bien se multiplican todos los valores absolutos y si hay una cantidad par de
factores negativos, el producto es positivo; si hay una cantidad impar de factores negativos, el producto es
negativo.
F) Propiedades de la multiplicación de números enteros :
a) Clausurativa: la multiplicación de números enteros es siempre otro número Z.
Ejemplo: Si a y b  Z
abZ
7  (– 6) = – 42
b) Asociativa: al agrupar los factores de diferente forma, siempre da el mismo producto.
Ejemplo: ( a  b)  c = a  (b  c)
(2  3)  (− 5) = 2  [3  (− 5)]
6  (− 5) = 2  (− 15)
– 30 = – 30
c) Conmutativa: el or den de los factor es, no altera el resultado o producto.
Ejemplo: a  b = b  a
12  (– 2) = (– 2)  18
– 24 = – 24
d) Elemento neutro : La producto de cualquier núm ero Z con 1, da com o resultado el m ismo núm ero
Z
Ejemplo: a  1 = a 83  1 = 83; ( – 47)  1 = – 47
e) Elemento nulo : el producto de un núm ero Z, da com o resultado = 0
Ejemplo: a  0 = 0  126  0 = 0
f) Distributiva: es la propiedad que relaciona la sum a o la resta con la m ultiplicación.
Ejemplo: a  (b + c) = a  b + a  c  3  (2 + 4) = 3  2 + 3  4
6 + 12 = 18
Fuentes Bibliográficas:










www.aaamatematicas.com/g83a_ax1.htm
www.thatquiz.org/es/previewtest?N
masmatematicaparavos.blogspot.com
aula.tareaplus.com
http://www.ditutor.com/
www.ematematicas.net
recursostic.educacion.es
contenidos.educarex.es
www.amolasmates.es
Imágenes de: matematicaadaptada1.blogspot
ecured.cu
i-matematicas.com
htor73.blogdiario.com
“NuNca coNsideres el estudio como una obligación, sino como una oportunidad para
peNetrar eN el bello y maravilloso muNdo del saber”
Albert Einstein