1. Healthcare

Grado 8
DESCRIPCIÓN DEL CONJUNTO DE NÚMEROS
ENTEROS
Clase
Nombre
Matemáticas
Observa la animación de la introducción y tenla en cuenta para responder las preguntas
de la actividad 1.
IL_M_G08_U01_L02_01_01_01
Figura 1. El trampolín
Introducción
Hace mucho tiempo, los chinos utilizaban bastoncillos de bambú o de madera para representar los
números y realizar en especial cálculos comerciales de una manera práctica, pero también para
tratar cuestiones relacionadas con los aumentos y disminuciones de magnitudes o con distancias
recorridas en sentidos opuestos; esos bastoncillos eran negros o rojos y representaban cantidades
positivas o negativas, de acuerdo con una atribución del color que es justamente la opuesta a la
empleada en la contabilidad occidental.
Los matemáticos hindúes del siglo VI mencionan también el uso de números negativos para tratar
este tipo de problema. Los antiguos griegos, por el contrario, rechazaron que pudieran existir tales
números.
En Europa medieval, los árabes dieron a conocer los números negativos de los hindúes, que en el
siglo XII se utilizaban ya ocasionalmente para designar las pérdidas en el análisis de cuestiones
financieras. Durante el Renacimiento, el manejo práctico de esos números en la contabilidad y
otros contextos, ayudó a su lenta introducción en las matemáticas. (Profesor en línea, (s.f))
La historia de los números ha sido determinante para la invención de algunos artefactos
que utilizan los números enteros como parte de su estructura.
Algunos artefactos en los que se puede ver el uso de los números enteros son los
ascensores, los cuales se mueven de manera vertical hacia arriba y hacia abajo.
Aumentando hacia arriba los números de los pisos y disminuyendo hacia abajo, y en
algunos sótanos o parqueaderos se usan los números enteros negativos para denominar
que se encuentran debajo del primer
piso.
Otro de estos artefactos |es el
termómetro, el cual nos permite
medir la temperatura por encima y
por debajo de cero, siendo las
Figura 3. Termómetro
cantidades por debajo del
cero las más frías.
Figura 2 Ascensor
IL_M_G08_U01_L02_01_02_02
IL_M_G08_U01_L02_01_02_01
Actividad 1: Definición del conjunto de los números enteros y descripción de sus
características
De acuerdo a la animación de la introducción y a la siguiente imagen, define que es el conjunto
de los números enteros y cuáles son sus características Figura 4. El ascensor
Figura 4. Ascensor en edificio
IL_M_G08_U01_L02_03_02_03
.
Definición del conjunto de los números enteros:
Actividad 2: Reconocimiento de los conjuntos del conjunto de los números enteros
1. Observa el siguiente diagrama del conjunto de los números enteros y luego completa la
siguiente frase, para ello usa las palabras que te dan como opciones:
IL_M_G08_U01_L02_03_04_01
-∞ … - 11 -10 - 9 -8 -7 -6 -5 -4 -3 -2 -1
0 1 2 3 4 5 6 7 8 9 10 11 ….
Figura 5. Conjunto de los números enteros
Conjunto de los números enteros
Entre otros, el conjunto de los números enteros contiene el _________ de los _________
__________
*principal
*conjunto
*números
*elementos
*naturales
Como pudiste darte cuenta, en el diagrama del ejercicio anterior se presentó el conjunto de los
números enteros, señalando cada uno de los conjuntos de dicho conjunto (el conjunto de los
números naturales o positivos y el conjunto de los números enteros negativos o también
llamados opuestos), lo cual se puede denotar por Z= {N U (0) U Z- }
2. Ahora escribe los números que están en el círculo de la izquierda y que
pertenecen al conjunto de los números enteros en el círculo de la
derecha.
,3
2.5 -3
A
-2
5
1
10,5
-5
-4
0
1/2
Z
3/2
4
3
2
-1
IL_M_G08_U01_L02_03_04_02
Figura 6. Diagramas de Venn
Actividad 3. Reconociendo el opuesto de un número.
Partiendo de tus saberes previos sobre el concepto de número opuesto, realiza el siguiente
apareamiento: lee las situaciones de las columnas A y B y luego relaciona cada cifra que
aparece en las situaciones de la Columna A, con la cifra que se le opone en la columna B.
Para ello, escribe el número de la columna Número situación, hasta la columna Número
situación con cifra opuesta que corresponda. Luego escribe en las columnas Cifra, la cifra
que representa la misma.
Número
Columna A
Cifra
Número Situación
con cifra opuesta
Columna B
Cifra
situación
1
2
3
4
Un avión se encuentra a un
a altura de 250 km.
Martina ha perdido en una
apuesta $250’000.000
El Polo Sur presenta una
temperatura de 35°c
bajo cero
Un submarino se
encuentra a una
profundidad de 250km
Juan se ha ganado una
lotería por $250’000.000
Un gran volcán exploto en el
año 470 después de cristo.
El filósofo Sócrates nació
en el año 470 antes de
Cristo.
La Costa Atlántica
presenta una
temperatura de 35°c
Actividad 4. Valor
absoluto de un número
De acuerdo a tus saberes previos sobre Valor absoluto, resuelve los siguientes ejercicios. Para
ello, haz clic en los botones de ejercicio.
1. Encuentra y señala en la sopa de números los valores absolutos de los números
listados en la tabla de la izquierda. Mira las instrucciones
Instrucciones:
Primero, elige el número de la tabla de la izquierda al que le buscarás el valor absoluto y coloréalo
con el color que desees.
Figura
Sopa de color
números
Luego, señala en la tabla de la derecha el valor absoluto y coloréalo
del7.mismo
que elegiste
en la columna de la izquierda. Para señalar los valores absolutos que tengan más de un dígito,
debes de colorear cada uno de los dígitos que conforman dicho número con el mismo color que
pintaste el número que elegiste en el primer paso.
Se pueden señalar números con varios dígitos de forma horizontal o vertical (no diagonal)
Sopa de números
5
-6
-5
4
-10
6
3
4
-297
2
9
7
9
6
7
1
-2
-5
-34
2
4
-8
-3
1
3
8
-1
8
Número
3
IL_M_G08_U01_L02_03_06_01
Figura 7. Sopa de números
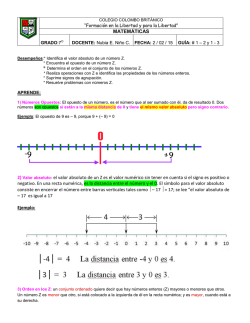
2. Si dos automóviles parten de un mismo punto cero a dos ciudades en sentido
contrario, y cada ciudad está a 2250 km del punto de partida, y asociamos la imagen
con la recta numérica, responde las siguientes preguntas:
0
2250km
Figura 8. Distancia
2250km
IL_M_G08_U01_L02_03_06_02
Preguntas:
a. El carro negro va hacia el lado __________ y este se representa con el signo ______
b. El carro amarillo va hacia el lado ___________ y este se representa con el signo _______.
c. ¿Con cuál o cuáles signos puedes representar la distancia a la que se encuentran las
ciudades? ___________ ¿Por qué?:
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
3. Responde las siguientes preguntas:
¿Qué es el valor absoluto de un número?
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
¿Cómo se representa el valor absoluto de un número?
____________________________________________________________________________
____________________________________________________________________________
Escribe 3 ejemplos de valor absoluto:
Cómo definición de valor absoluto podemos decir:
Si tienes un número negativo, por ejemplo -5, su valor absoluto es su opuesto, es decir:
-5 = 5 , y si tienes un número positivo por ejemplo 8, el valor absoluto del número es el
mismo número positivo, es decir 8 = 8
Actividad 5. Ubicando números enteros sobre la recta numérica
Ubica el número dado, sobre la recta y escribe el antecesor y el sucesor de dicho número,
señalándolos con A o S, según corresponda.
IL_M_G08_U01_L02_03_07_01
-5
Figura 9. Recta
12
+1
-11
Actividad 6. Ordenando y comparando números enteros
Ubica los números de la siguiente lista hasta el lugar correcto sobre la recta numérica, y luego
escríbelos de mayor a menor y de menor a mayor en los recuadros, de tal forma que se
cumplan las relaciones planteadas.
Luego escribe algunas conclusiones sobre las relaciones de los números ordenados según los
signos < y > y socialízalas en la clase.
-11
es>
es <
es>
es <
+1
es>
es <
Actividad 7. Las leyes de los signos
-7
-2
es>
+13
-1
es>
es<
+5
es>
es<
+8
-6
es>
es <
es>
es <
es <
En esta actividad recordaremos las leyes de los signos, necesarias para resolver operaciones de
suma, resta y multiplicación con enteros. Observa la tabla con atención, en la cual se
incluyeron números al azar, y luego resuelve los ejercicios:
Entonces, ¿cuál es el resultado de multiplicar dos factores
con signos iguales o hacerlo con factores con signos
contrarios? Socializa tus respuestas en la clase.
Figura 10. Leyes de los
signos
Ejercicio 1
IL_M_G08_U01_L02_03_08_01
Realiza las siguientes multiplicaciones con números enteros teniendo en cuenta las
leyes de los signos. Copia en el espacio el factor o el producto que corresponda.
a) 4 • 5 • (-20) • 6 = 20 • ____ • 6 = _____ • 6 = ___
b) (-3) • (-4) • (-5) • (-6) • -2 = _____• 30 • (- 2) = _____ • (- 2) = _____
c) 8 • (-6) • (-4) • 5 • (-6) • 3 = (-48) • (-4) • 5 •_____= (-48) •____• -18 = (-48) • _____= _____
Ejercicio 2
Ahora completa las frases y responde las preguntas
1. Multiplicar cuatro factores con signos iguales dan resultados ___________.
2. Multiplicar cuatro factores, tres con signos iguales y uno con signo contrario, dan resultados
___________.
3. Multiplicar cinco factores con signos iguales dan resultados _________ o ___________.
4. El producto entre dos números enteros es -1170 y uno de los factores es -26 ¿cuál es el
valor del otro factor?
Actividad 8. Suma, resta y multiplicación de números enteros
En esta actividad resolveremos sumas, restas y multiplicaciones teniendo en cuenta los
signos de agrupación. Para ello resolveremos un ejemplo.
Para resolverlo seguiremos los siguientes pasos
•
Elimina los signos de agrupación efectuando las operaciones de los signos de
agrupación más internos hasta efectuar las operaciones de los más externos.
•
Recuerda que si un signo de agrupación esta precedido de un signo menos esto
implica utilizar la ley de los signos.
•
Suma números positivos entre sí y negativos entre sí. Efectúa la operación sumando
los dos resultados.
Ahora resuelve los siguientes ejercicios:

{35 + (54 − (−37 − 35). (−25) + 82)}

−{52 − [36 − 58 − (24 + 82) + 36] + 32 + (−42)}

{−[27 − 3 • (120 + (−170)) + 25] + 5 • (34 − 49)}
Ahora observa la animación de la actividad y compara lo que hiciste con lo que plantea esta.
¿Se cumplen los casos presentados?, socializa tus conclusiones con los compañeros
Suma,
resta y
multiplic
ación con
enteros
Suma,
resta y
multiplic
ación con
enteros
Suma,
resta y
multiplic
ación con
enteros
Figura 11. Libro
IL_M_G08_U01_L02_03_12_01
Aquí te presentamos un resumen
Suma de enteros
Signo del 1er
sumando
Operación
Signo del 2o
sumando
Signo del
resultado
Ejemplo
Positivo (+)
(+)
Positivo (+)
Positivo (+)
Negativo (-)
(+)
Negativo (-)
Negativo (-)
Positivo (+)
(+)
Negativo (-) Signo del mayor
Negativo (-)
(+)
Positivo (+) Signo del mayor
5 + 7 = +12
( Se suman los valores absolutos de los
números)
-5 +(- 7) = -12
( Se suman los valores absolutos de los
números)
5 + (-7) = -2
( Se restan los valores absolutos de los
números)
-5 + 7 = 2
( Se restan los valores absolutos de los
números)
Resta:
Recuerda que la resta en los números enteros se puede definir como la suma
de un número con el opuesto del sustraendo
En la multiplicación de dos factores: si los dos factores tienen igual signo, el
producto es positivo, y si los dos factores tienen distinto signo, el producto es
negativo, por ejemplo:
(+4) • (+3) = +12
(-4) • (+3) = -12
(-4) • (-3) = +12
(+4) • (-3) = -12
Suma,
resta y
multipl
icación
con
entero
s
Resumen
Tareas
Tarea 1. A partir de los valores que aparecen en las columnas a, b y c, resuelve las
operaciones que se indican en las siguientes tres columnas:
a
b
c
2
6
3
4
-2
5
-3
3
4
-4
1
-2
a+(b + c)
b • [c-(a + b)]
- [a + b • (- c)]
Realiza aquí los respectivos desarrollos:
Tarea 2. Lee la siguiente situación y después responde
Un termómetro marca a las 7 a.m. una temperatura de 8°C grados
7:00 AM
y
8.0° C
durante el día tiene los siguientes movimientos:

A las 10 a.m. la temperatura sube 25°C.

A la 1 p.m. baja 17 °C.

A las 4 p.m. el termómetro está marcando 22°C, y

A las 7 p.m. la temperatura baja a 15°C.
IL_M_G08_U01_L02_05_16_01
Figura 12. Termómetro
Responde:

¿Qué temperatura marca el termómetro a las 10:00 a.m.? ____

¿Cuál es la temperatura a la 1:00 p.m.? _____

¿Cuál es la diferencia de temperatura entre la 1:00 .pm. y las 4:00 p.m.? ____

¿Cuántos grados marca a las 7:00 p.m.? ____

¿Qué diferencia hay entre la temperatura de las 7:00 a.m. y las 7:00 p.m.? _____
Tarea 3.
A partir de la siguiente situación resuelve:
En un tanque hay 200 L de agua. Si se abre una llave en la parte
superior para que deposite 23litros del líquido por minuto y al mismo
momento se abre otra llave que se encuentra en la parte inferior del
depósito para que riegue externamente 14 L de agua por minuto. Si
se dejan abiertas las dos llaves por 12 minutos…
a. ¿Cuántos litros de agua quedan en el tanque la cerrar las llaves?
_______
b. ¿Cuántos litros de agua hay a los 8 minutos de haber abierto las
llaves? ______
Figura 13. Caneca
IL_M_G08_U01_L02_05_16_02
Tabla de Figuras
Figura 5. El trampolín
Figura 6. El ascensor
Figura 7. Termómetro
Figura 8. Ascensor en edificio
Figura 9. Conjunto de los números enteros
Figura 10. Diagramas de Venn
Figura 7. Sopa de números
Figura 8. Distancia
Figura 09. Recta
Figura 10. Leyes de los signos
Figura 11. Libro
Figura 12. Termómetro
Figura 13. Caneca
Bibliografía
Hipertextos 7. (2010). Santillana.
C. Boyer. (1987). Historia de la matemática. Alianza Universidad.
Sánchez , L. E., & Restrepo , M. (2011). Matemáticas para pensar 7. Norma.
Profesor en línea (Sf) Números enteros(z) Recuperado de
http://www.profesorenlinea.cl/matematica/NumerosEnterosZ.htm