1. Art and Diseño

I.D.4
I
Nuclear Physics A91 (1967) 123--132; (~) North-Holland Publishiny Co., Amsterdam
d
Not to be reproduced by photoprint or microfilmwithout written permissionfrom the publisher
QUALITATIVE DESCRIPTION
OF NUCLEAR COLLECTIVITY
G. F. BERTSCHt, R. A. BROGL1Att and C. RIEDELttt
The Niels Bohr Institute, Unit'ersity of Copenha#en, Denmark
Received 13 July 1966
Abstract: The characteristic feature of many types of collective states in the shell model is a spatial
correlation between particles and holes. Several examples are discussed, which clarify the relation between different types of collectivity.
1. Introduction
The p r o p e r t i e s o f m a n y - b o d y systems m a y often be better u n d e r s t o o d by studying
the wave function in configuration space. F o r example, in nuclei with closed shells
plus or minus two particles, an attractive short-range force produces clustering
between the two particles or holes. Large t w o - b o d y transfer matrix elements, as for
e x a m p l e in the (t, p) stripping reaction, m a y then be u n d e r s t o o d simply from the
large overlap between the correlated t w o - n e u t r o n wave function in the triton, and
the correlated wave function in the residual nucleus g r o u n d state.
L o o k i n g at the spectrum o f a single nucleus, there are usually just a few states,
either very high or very low in the spectrum, that collect most o f the electro-magnetic
transition strength to the g r o u n d state :. This is quite well u n d e r s t o o d in terms o f
H a m i l t o n i a n d y n a m i c s in the shell model with realistic forces. The wave functions
that result, which are c o m b i n a t i o n s o f shell-model orbitals, are not very transparent,
a n d therefore we l o o k in c o o r d i n a t e space for a better understanding.
W h e n the g r o u n d state can be treated as a closed-shell nucleus, the excited states
which m a y be reached by the o n e - b o d y electromagnetic transition o p e r a t o r will have
one particle and one hole. To treat the wave function as simply as possible, we
consider only the correlations between the particle and the hole. To keep the concept o f
hole definite, the particle-hole f o r m a l i s m is reviewed in the section below. Then the
qualitative features o f the idealized electromagnetic multipole states and the m o r e
physical energy eigenstates are discussed. Finally, clarification is given for the results
o f Broglia and Riedel 2) for the calculation o f the 2°6pb(t, p ) 2 ° a P b stripping reaction,
where cross sections to the g r o u n d state and collective states were all enhanced ~4).
t National Science Foundation Fellow. Present address: Palmer Physical Laboratory, Princeton,
N.J.
tt Fellow of Universidad de Buenos Aires, Facultad de Ciencias Exactas, Departamento de Fisica.
ttt Permanent address: Zentralinstitut fiir Kernforschung, Rossendorf bei Dresden, Germany
(GDR).
For a recent review of the theory and experimental data on collective states, see ref. 1).
123
G.F. BERTSCHet al.
124
2. The hole wave function
By the hole wave function [a~-'), we mean the Slater determinant ]~1~ 2 . . . ~.-1
~ . + ~ . . . ) , which has the closed-shell orbitals in the usual order but with the orbital
~. missing. The properties of holes are naturally defined by taking the overlap of
the hole wave function with the Slater determinant of the closed shell and studying
the properties of the particle left from the closed shell after integrating out all possible
coordinates. Thus, the matrix element of a hole with an arbitrary state or operator
( f l is defined as
{fl~ -1) -
(closed shell[closed s h e l l - ~ . ) l f )
= ( c ~ , l f ) ( - 1)".
(1)
An example is the basic formula for expressing the particle-hole wave function in
configuration space
(rv~,jfl~; 1) =
{r~l//)(~.lr.)(- 1)".
(2)
The only differences from the particle-particle expression are that anti-symmetrization
is not called for, and that an occasional factor of ( - 1 ) appears.
We may try to generalize the concept of hole state to situations where there are
no closed shells. In this case, the basic configuration corresponding to the closed
shell is the sum of Slater determinants. The hole state I:t-1) includes only those determinants in the sum which originally had the orbital :t with relative amplitudes equal
to the relative amplitudes of the basic configuration. There are difficulties with this
definition in that the hole states are not naturally normalized and not necessarily
orthogonal to each other. The states can always be redefined in the end to make them
normalized, but the second difficulty is crucial if a physical and graphic interpretation
is to be given to the hole states. For particle-hole excitations based on the pairing
ground state the difficulty is not serious. When a pair is broken, the resulting particlehole wave function is orthogonal to the ground state and to every other two-quasiparticle state except the one obtained by time reversal. In fact,
I/~,,,~-'7
= I~-./~:'.,).
(3)
The relative spatial coordinate between particle and hole retains significance, but
the distinction between particle and hole is blurred.
3. The pure multipole states
The electric L-pole operator is
~, (½-- ½zz)r~ yL( i ).
i
(4)
NUCLEAR COLLECTIVITY
125
Then the state which exhausts all of the L=pole strength from the closed=shell ground
state is
proton
Y.i
=
Z <a; ]1"LY
p,h
lah÷ > ( a p+
ah)
]>.
(S)
This state is first divided into a part with T = 0 and a part with T = 1, each receiving
half the strength. Since there is no spin dependence in the electric operator, the
particle-hole state must have S = 0.
The spatial part of the wave function may be characterized nearly as simply as
the spin and isospin degrees of freedom. First, observe that the electric operator may
be written in configuration space and with the help of a second-quantized notation as
Ir;>6( r, - r;)r~yL(i)(r,] = Z a+(ctlr;)O( r, --r;)r~yL(i) ~. (r, lfl>ap.
i
~t
/3
We now study the effect of this product at a particular position r. The particle annihilation factor tries to give a hole localized at r. Of course this localization is limited by
the uncertainty of the particle position within the closed-shell ground state. Similarly,
the particle creation factor tries to create a particle at the same position but is also
somewhat limited, because the a + arc only effective above the Fermi sea and thus do
not span the configuration space. The resulting particle-hole pair located approximately at r is multiplied by r L yL and rotated to produce a wave function which
transforms properly under rotations.
A convenient way to project out the relative probability distribution is to require
that the hole be on the z-axis and integrate out the radial wave functions, leaving
the angular distribution of the particle. For each value M of the azimuthal quantum
number of the total wave function, there will be an independent contribution to
the particle distribution. The operator for localizing the particle on the z-axis is
]/?)+l
<]r[, cos 0 = II = ~ , T n
<rlq~,>a,..o,
(6)
where a ~1~, 0 annihilates a particle in the ~ orbital with angular momentum quantum
numbers J, M = 1,, 0. The total expression for the angular distribution is then
M
P(~, 2) = ~ (-- 1)ta-'a'<4'~l~='><4)al4~a'>C~a C~.a,
~t', fl"
× ,/(21~+1)(2!a._~-1) y~=.(Qt2)Y~.(~t2)(I~IaMOILM)(I~,Ia.MOILM).
(7)
4n(2L+ 1)
Here C~a is the amplitude of the state a+aa[> in the particle-hole wave function.
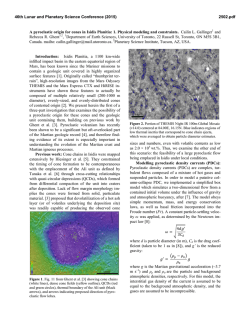
In fig. 1, the relative angular distribution is plotted for the dipole state in oxygen and
126
G . F . BERTSCH et aL
i
3'
2
(X
O..
1
i
1.0
1
'
0
i ._
I
-1.3
COS 212
Fig. l. The particle-hole angular correlation function for a) the pure dipole state of teO and b) the
pure octupole state of 4°Ca. In the case of t60 there are two shell-model states that are mixed together
and in 4°Ca there are ten states mixed. Harmonic oscillator single-particle orbitals are used throughout.
I
I
'"
I-Z
O
O
g~
I
PARTICLE
COORDINATE
Fig. 2. The radial wave function for the octupole state of Ca with both particle and hole on the z-axis.
The contours show the position of particle and hole where the probability density reaches 50~. and
"/5 ~ of its maximum value. The broken line indicates the nuclear surface, defined as the radius
where the density is ~ of its central value.
NUCLEAR COLLECTIVITY
127
the octupole state in calcium. The normalization is such that
f
= 1.
+IP(f2,z
(8)
-1
The correlation is not really good until several shells, both in particle orbitals and
hole orbitals, can be mixed. In fig. 2, the radial wave function of the pure octupole
state of Ca is indicated in contour for the relative angle cos f212 = 1. There are no
striking features; the radial distribution is determined mainly by the factor r L, which
places both particle and hole on the surface. In fig. 3, the distribution of the particle_...~
7! i.
d
i
13-
I
~0
I
I
._
i
0
1
i
t
-'~0
COS ~ 12
Fig. 3. T h e particle-hole correlation function for a 2 ~ state o f tt+Sn. T h e 16 valence particles are
limited to the single-particle orbitals (s,l. , d k , d~., g i , h ¥ ) a n d the wave function is chosen to m a x imize the q u a d r u p o l e strength from the pairing g r o u n d state.
hole is plotted for the 2 + multipole state of ll6Sn. The ground state is the pairing
state with the parameters i2) of Kisslinger and Sorensen, and only states within
their configuration space are included. As mentioned above, here there is a loss of
distinction between particle and hole. If virtual deformations are allowed in the
ground state 12), then the simple ideas about particles and holes break down completely. This picture of the 2 + state agrees with the usual picture of vibrations, in
that the static shape is nearly spherical 13) even though there is a large off-diagonal
matrix element.
4. Energy eigenstates
When shell-model states are diagonalized with a realistic Hamiltonian, the principal
effect in configuration space is to produce correlations between particles of different
128
G . F . BERTSCH et aL
kinds. For example, if several configurations were added to the basic f.~d~ 1 configuration of the 4°K ground state wave function, there would be a slight enhancement
of the proton wave functions at the co-ordinate of the valence neutron. In the particlehole picture, there would be a decrease in the proton hole wave function at the
neutron co-ordinate. This is because within a closed shell there are anti-correlations
between particles from the exclusion principle. An outside particle which correlates
with the particles in the shell must therefore anti-correlate with the holes.
Different reasoning applies to the excitations of closed-shell nuclei, when we consider either the highest or lowest states in a particle-hole spectrum. As is well known
(refs. 3- 5)), the spin and isospin degrees of freedom play a major role in determining
these states, with the T = 0, S = 0 excitations brought down in energy, and the
T = 1 excitations raised above the shell-model single-particle energies *.
The mechanism is simply that there is a resonance between excitations of unlike
particles, splitting an intrinsic degeneracy. The interaction among particles of the
same kind is weak, because of anti-symmetrization and the short range of the realistic
forces. Thus the spatial part of the wave function for the lowest and highest
states will be the one which allows maximum oif-diagonal matrix element mixing
excitations of different kinds of particles. In the approximation that the singleparticle orbitais are degenerate, we expect similar spatial wave functions for the
highest T = 1 states and the lowest T = 0 states.
To see what kind of correlations are produced by the second-order matrix element
determining the spatial wave function
(Ppl Vlnn)(nn[ V[p'p'),
(9)
we look at the matrix element in co-ordinate space,
( ¢ p ( r p ) ¢ ; ' (ro)[ Vl ~.(r.)¢,~ ' (r~)).
(I O)
It is clear that a local force will allow this matrix element to be large only when
rp = ri~.
(11)
Thus particle-hole correlations will be favoured, making the eigenstate resemble the
pure multipole state. However, since the single-particle levels are more important
than the residual force in determining the eigenstates, the particle and hole will not be
correlated as well as in the pure muhipole states.
For most nuclei, the energetics of the single-particle orbitals requires that the
particle or hole be limited to shells of one parity. This gives a restriction on the
relative angular distribution, making it symmetric about 90 °.
* For heavy nuclei, T and S are not useful q u a n t u m numbers. Instead, one can say that the lowest
eigenstates have neutron amplitudes in phase v, ith proton amplitudes and the largest a m o u n t of
S ~ 0 strength allowed by the single-particle splittings, provided of course there is sufficient degeneracy in the single-particle states.
NUCLEAR
129
COLLECTIVITY
£L
[
I
I
]
10
I
I
[
0
-1.0
COS ~l~
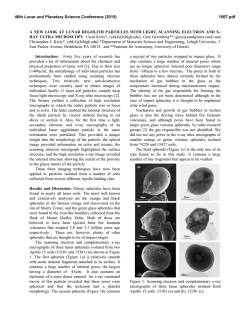
Fig. 4. T h e particle-hole correlation function for the S = 0 part o f the lowest 3 - state in calcium
f o u n d by a T a m m - D a n c o f f shell-model diagonalization. T h e relevant part o f t h e wave function,
which h a s been normalized to 1 for plotting the graph, is
tp = [ 0 . 5 5 ( f d - l ) s + 0 . 5 1 ( f l s - 1 ) 3 + 0 . 3 2 ( I p d - a ) 3 - - 0 . 0 4 5 ( g p - l ) 3]
(S = 0)4- . . •
......
:3-
.
1
• C,JRViL C
-.
L
D.
I
i
,
10
0
COS
8
L_..
-I0
Q.~
Fig. 5. T h e particle-hole correlation for 3- wave functions o f z°sPb. Curves a) a n d b) use t h e S = 0
part o f t h e n e u t r o n excitation o f the first a n d second 3 - states, which e x h a u s t 36 70 a n d 10 ~ o f
t h e total probability o f these states, respectively. Curve c) is the S = 0 p r o t o n - p r o t o n hole correlation o f the lowest 3-, which has 37 ~ o f the total strength o f this state.
130
G . F . BERTSCH et al.
Turning to the radial degree of freedom, the Hamiltonian dynamics always favour
placing the particle and hole on the nuclear surface when cos f212 = I, in agreement
with the configuration of the pure multipole state.
The first example of an energy eigenstate is the 3- vibration of calcium found by
Mavromatis 6) by diagonalizing a realistic force 7) in the s-d shell for the hole and
the p-f shell for the particle. To this we have added in perturbation theory the configuration (gp-1)3 to provide an idea of the parity mixing in the single-particle wave
function. The relative angular distribution of the particle and hole is plotted in
fig. 4 for the S = 0 part of the wave function. This exhausts 66 ~o of the entire wave
function. There is a good correlation, but barely distinguishable asymmetry about
90 °.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3L
i
i
rl
1
:
,:
k. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .~. . . . . .
lo
__1
-lO
cos
~ ~2
Fig. 6. T h e particle-hole correlation for 5- wave functions o f 2°sPb. Curves a) and b) are the S = 0
parts o f the n e u t r o n excitation o f the first a n d second 5- states.
Gillet and collaborators s) have calculated wave functions for low-lying 3- and
5- states in 2°8pb. Figs. 5 and 6 show the particle-hole angular distributions of the
S = 0 part of their particle-hole wave functions.
5. Particle-particle and hole-hole wave functions
For the discussion of the stripping reaction 2 ° 6 p b ( t , p ) 2 ° s p b , it is useful also to
consider the hole-hole correlations in 2°6pb and the particle-particle correlations in
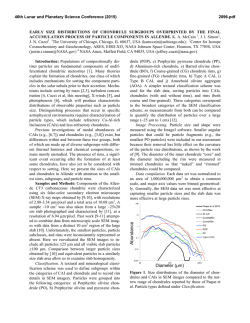
2t°pb. As may be seen in figs. 7 and 8, the pairing wave functions give rather strong
clustering. For both the particles and holes, there is one orbital of opposite parity in
the wave function that provides the polar asymmetry.
NUCLEAR COLLECTlVXTY
131
B~s and Broglia 9) have considered a 2°8pb excitation, the pairing vibration, which
is defined by adding two neutrons coupled to 0 + in the post-2°spb shells to the ground
state of the 2°6pb nucleus, which has the holes scattering only below the Z°spb
n
1
10
0
-1.0
COS ~ ~z
Fig. 7. The correlation o f holes with S = 0 in s°gPb. The wave function was determined from the
superconductivity equations with single-particle levels from ref. 1~) and pairing parameter 18.1/A
MeV.
4
"L
d
13_
(3
'0
cos
Fig. 8. The correlation o f particles with S
-
0
~'2
=
0 in 21°Pb with pairing wave function
132
G.F. BERTSCH et aL
energy gap. This results in a 2P-2H wave function with particle-particle correlations
and hole-hole correlations given by the 2 ~opb and 206pb wave functions, respectively,
but no correlation between particles and holes. According to the discussion in sect. 4,
there should be some repulsion between the particles and holes. In fact for lighter
nuclei, such as 160 and 4°Ca, the lowest 2P-2H states are the SU(3) wave functions
of maximum weight 1o), which have the particles along one axis and the holes in the
perpendicular plane. However, calculating in perturbation theory, it is found that
in the Pb-region the particle-hole force is too small to disturb the pairing vibration
significantly.
6. Two-body transfer
It is now possible to see in a qualitative way why the 2°6pb(t, p)2°spb reaction
excites the ground state, collective states, and a 0 ÷ excitation strongly 2, ~4). The
two particles that ale added will be quite close together, at least in the framework of
DWBA theory. There are three possibilities for adding them to the holes of the 2°6pb
wave function. They can fill the holes, which happens quite easily since the holes are
also close together. This corresponds to the ground state transition.
The strength to the pairing vibration is also coherent with the two particles placed
close together but in higher shells.
Finally, if one of the particles fills a hole, then by the above geometrical considerations the other particle is likely to be close to the remaining hole. With the usual
optical potentials, all the reaction takes place on the surface of the nucleus. Thus,
the states strongly populated will be like the electromagnetic multipole states and
the lowest energy eigenstates.
The authors wish to acknowledge Professor A. Bohr for carefully reading the
manuscript and for the hospitality of the Niels Bohr Institute.
References
I)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
A. M. Green, Repts. Progr. Phys. 28 (1965) 113
R. A. Broglia and C. Riedel, to be published
G. E. Brown and M. Bolsterli, Phys. Rev. Lett. 3 (1959) 472
G. E. Brown, L. Castillejo and J. A. Evans, Nuclear Physics 22 (1960) 1
G. E. Brown, J. A. Evans and D. J. Thouless, Nuclear Physics 24 (1960) 1
H. Mavromatis, P h . D . thesis, Princeton University
A. Kallio and K. Kolltveit, Nuclear Physics 53 (1964) 87
V. Gillet, A. M. Green and E. Sanderson, private communication
D. B~s and R. A. Broglia, Nuclear Physics 80 (1966) 289
D. M. Brink and G. F. Nash, Nuclear Physics 40 (1963) 608
E. K. Hyde, 1. Perlman and G. T. Seaborg, The nuclear properties of the heavy elements
(Prentice-Hall, Englcwood Cliffs N.J., 1964)
12) L. S. Kisslinger and R. A. Sorensen, Mat. Fys. Medd. Dan. Vid. Selsk. 32, No. 9 (1960)
13) T. Tamura and T. Udagawa, Phys. Rev. Lett. 15 (1965) 765
14) J. H. Bjerregaard, O. Hansen, O. Nathan and S. Hinds 89 (1966) 337