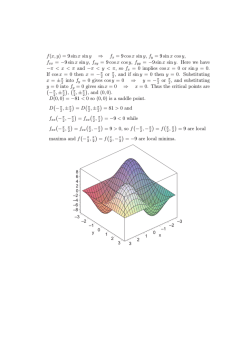
documento 487674
ID: 1 AP Calculus AB Name___________________________________ Integration by Parts Date________________ Period____ ©6 X2L0G1v5W sKsuStKa6 USIoofXtSwnaRr4ej 1LFLbCd.Z 7 JAGlElS ur1i1gEhPttsY grveysheIrSvme7dP.B Evaluate each indefinite integral using integration by parts. u and dv are provided. 1) 3) ∫ ln x dx; u = ln x, dv = dx ∫ ln x 1 dx; u = ln x, dv = 2 dx 2 x x 2) ∫ xcos x dx; u = x, dv = cos x dx 4) ∫ tan −1 x dx; u = tan −1 x, dv = dx Evaluate each indefinite integral. 5) ∫ x 2 ln x dx 6) ∫ 7) ∫ x sin x dx 8) ∫ x ⋅ sec x dx 2 ©i L2X0Y195p kKVuytsaa ySFowfRtKw3akrUe4 aLHLSCt.R O EASlHlQ Dr6iVgphAtZsb 1ruewsOeGrivoegdX.N S 8MqaQdReo dwAiitNhb QIdnPfNiqnpiEtCeU MCPaulfc6unlHuasp.L x xe dx 2 Worksheet by Kuta Software LLC ID: 1 AP Calculus AB Name___________________________________ Integration by Parts Date________________ Period____ ©l L2w021B57 9K5u8tAaY 0SdoRfhtxwaabrwe5 HL4LaC1.p r TAelBle NrPihgqhttRsG xrTelsbeFr7vBeHdX.E Evaluate each indefinite integral using integration by parts. u and dv are provided. 1) ∫ ln x dx; u = ln x, dv = dx 2) ∫ xcos x dx; u = x, dv = cos x dx x ln x − x + C 3) ∫ xsin x + cos x + C ln x 1 dx; u = ln x, dv = 2 dx 2 x x 4) ∫ tan − ln x − 1 +C x −1 x dx; u = tan −1 x, dv = dx xtan −1 x − ln ( x 2 + 1) +C 2 Evaluate each indefinite integral. 5) ∫ x 2 ln x dx 6) Use: u = ln x, dv = x 2 dx x 3 ln x x 3 2 x ln x dx = − +C 3 9 x Use: u = x, dv = e dx ∫ 7) ∫ x sin x dx 2 ∫ x xe dx ∫ xe dx = xe − e + C x 8) x x ∫ x ⋅ sec x dx 2 Use: u = x 2 , dv = sin x dx Use: u = x, dv = sec 2 x dx ∫ x sin x dx = −x cos x + 2xsin x + 2cos x + C ∫ x ⋅ sec x dx = xtan x + ln cos x + C 2 2 ©y h2X0J155K BKau3ttai PSBoMfotcwXawrweW yLcLdCi.r L 5Aul7l5 9rMivgwhTtssV WrTelsEeHrgvKeedK.I L CMhaQdQeQ 6wIiLtXhs EIentfRiinMi4tPe3 9CHagl8csuTlau8sc.2 2 Worksheet by Kuta Software LLC
© Copyright 2026