1. No category

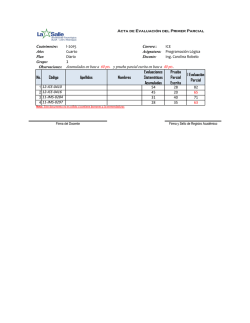
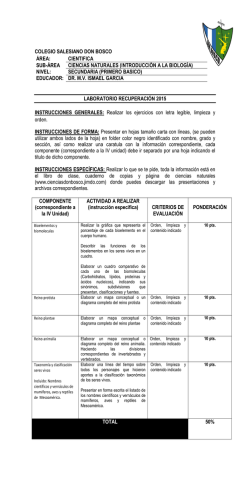
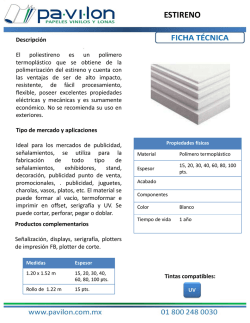
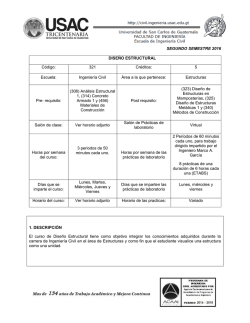
Curso 2015-2016
IES Montevives. Departamento de Matemáticas.
Control Temas 2 y 3. Derivadas. Aplicaciones de las
derivadas.
Nombre:
1.- (1.5 pts) Calcula lı́m
x→0
ln(1 + x) − sen x
x · sen x
2.- (1.5 pts) Sea la función f : R → R definida por f (x) = x3 + ax2 + bx + c.
Se sabe que tiene un punto de derivada nula en x = 1 que no es un extremo
y que f (1) = 1. Calcula a, b y c.
3.- (1.5 pts) Partimos un hilo metálico de longitud 1 m en dos trozos, haciendo con uno un cuadrado y con el otro un cı́rculo. Calcula las dimensiones
de cada trozo para que la suma de las áreas sea máxima.
x
4.- (2 pts) ¿En qué punto de la gráfica de la función f (x) = e 3 la recta
tangente a ésta pasa por el origen de coordenadas?
5.- (1.5 pts) Estudia los intervalos de crecimiento y decrecimiento de la fun2
ción f (x) = x2 · e−x . Determina cuáles son sus extremos, indicando de
qué tipo son.
x2 + ax + 6
cumpla
x2 − 2x − 12a
las condiciones del teorema de Rolle en el intervelo [−3, 3]. Calcula los
puntos de la gráfica en el intervalo en el que la tangente es horizontal.
6.- (2 pts) Determina a, para que la función f (x) =
1