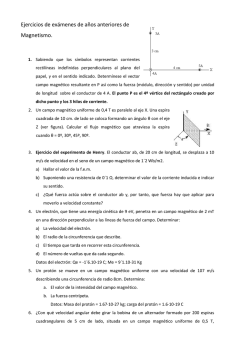
4. El conductor rectangular de la figura de dimensiones
Procedimientos selectivos profesores secundaria Valencia, Física y Química [email protected] Revisado 12 mayo 2016 2009 4. El conductor rectangular de la figura de dimensiones 0,6 m por 0,3 m, cuya resistencia es de 2,7 ohmios, se encuentra en el interior de un campo magnético B=(5-y) i (SI) y se desplazo en la dirección del eje OY en su sentido positivo. Sabiendo que en el instante inicial el lado izquierdo del conductor rectangular coincide con el eje OZ, calculad la intensidad de corriente que circula en los casos siguientes: a) Si el conductor se desplaza con velocidad constante de 1,5 m/s2. b) Al cabo de 20 s de comenzar su movimiento, partiendo del reposo, con una aceleración de 3 m/s 2 Se dispone de enunciado original escaneado y se cita literalmente. Se asume que se pretendía indicar velocidad constante de 1,5 m/s. Planteamos la expresión de flujo para utilizarla la ley de Faraday Como el campo magnético siempre tiene la misma dirección perpendicular a la superficie de la ⃗ · dS= ⃗ ∫ B·S espira, podemos prescindir de vectores Φ=∫ B El campo magnético depende de y, por lo que es constante en un diferencial de superficie de altura 0,6 y de anchura dy, dS=0,6·dy y+0,3 ( y + 0,3)2 y 2 y+0,3 y2 Φ=∫ y (5− y)· 0,6 ·dy =0,6 [5 y− ] =0,6 5 ( y +0,3)− −5 y + 2 y 2 2 2 2 y 0,6 y 0,09 y Φ=0,6(5 y +1,5− − − −5 y + )=0,873−0,18 y [Φ en Wb , y en m] 2 2 2 2 a) Si la velocidad es constante, y=y0+vt, siendo y0=0 −d Φ −d (0,873−0,18 vt) ε= = =0,18 · v=0,09 · 1,5=0,27V dt dt V 0,27 Usando la ley de Ohm I = = =0,1 A R 2,7 b) Si la aceleración es constante, y=y0+v0t+½at2 , siendo y0=0, v0=0 1 2 −d (0,873−0,18 at ) −d Φ 2 ε= = =0,18 at=0,54 t [ε en V , t en s ] dt dt Para t=20 s ε=0,54 · 20=10,8 V V 10,8 Usando la ley de Ohm I = = =4 A R 2,7 ( )
© Copyright 2026