1. No category

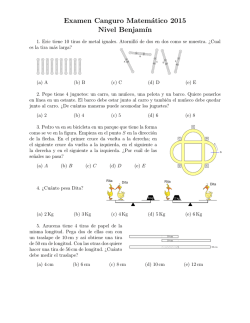
XI Convocatoria Nacional
Academia Sabatina Jóvenes Talento
Nicaragua 2015
Nivel 1
Quinto y Sexto Grado
Problema 1
Hank colocó una clave de cuatro dı́gitos a su maleta. Escribió la lista: 7032, 5413, 2730, 4985, 4071,
6325, 9417, 6319, 2694, con la condición de que en cada número hay uno y sólo un dı́gito que ocupa
la misma posición del número clave. ¿Cuál es la clave en la maleta de Hank?
Problema 2
Oliver le dice a Matilde: “Estoy pensando en un número de dos cifras, el producto de esas dos
cifras es 36”. Al ver las posibilidades, Matilde pide más datos, a lo que Oliver responde: “Te podrı́a
decir la suma de sus cifras, pero no serı́a suficiente para que supieras con seguridad el número que
pienso. En lugar de eso, te diré que mi número es menor que 80”. ¿En qué número está pensando
Oliver?
Problema 3
El tablero de la figura siguiente muestra caritas tristes y caritas felices. Un
juego consiste en cambiar de expresión a todas las caritas de una misma
fila, columna o diagonal (Por ejemplo: una carita feliz se convierte en una
triste y viceversa). ¿Es posible llegar a obtener un tablero en donde todas
las caritas sean felices? Justifique su respuesta.
/
,
/
,
Problema 4
Te presentamos el siguiente juego: consiste en tomar 10 monedas o fichas
disponiéndolas en un cı́rculo como muestra la figura. Los jugadores se turnan para sacar una o dos fichas, pero si se sacan dos, éstas deben estar una
junto a otra, sin que haya entre ellas ninguna otra ficha o espacio vacı́o. La
persona que saca la última ficha es la que gana. Si ambos jugadores juegan
racionalmente, ¿quién de los dos ganará y cuál estrategia deberá utilizar?
,
,
,
/
,
,
/
,
,
,
,
,
Problema 5
El segmento AB conecta dos vértices opuestos de un hexágono regular y el segmento CD conecta
los puntos medios de dos lados opuestos, como se muestra en la figura. Encuentre el producto de
las medidas de los segmentos AB y CD si el área del hexágono es 60 cm2 .
C
B
A
D
1
XI Convocatoria Nacional
Academia Sabatina Jóvenes Talento
Nicaragua 2015
Nivel 2
Séptimo y Octavo Grado
Problema 1
Del conjunto de los números naturales se suprimieron los cuadrados perfectos (1, 4, 9, 16, . . .) y los
cubos perfectos (1, 8, 27, 64, . . .). De los números que quedaron, considere los 2015 números más
pequeños. ¿Cuál es el mayor de estos 2015 números?
Problema 2
Halle el menor entero positivo n que tiene la siguiente propiedad: El menor múltiplo de n que está
formado solamente por dı́gitos 0 y 1, es el 1110.
Problema 3
Sobre la circunferencia de un parque hay una hilera de árboles y en cada uno de ellos hay un loro.
De vez en cuando dos loros en árboles diferentes vuelan simultáneamente hacia árboles vecinos,
pero en direcciones opuestas. Decida en que caso es posible que todos los loros, en algún momento,
se encuentren sobre el mismo árbol.
Problema 4
Una barra de chocolate tiene forma de cuadricula de 4 × 7, con un cuadrito en un esquina marcado
con X. Andrés y Berta juegan de la siguiente manera: cada uno en su turno, comenzando por
Andrés, debe partir la barra en dos por una de las lı́neas rectas de la cuadricula, comerse el trozo
que no contiene a la X y pasarle lo que queda al otro jugador. El que no pueda partir la barra (lo
que ocurrirá cuando reciba solamente un cuadrito) pierde el juego. Determine si alguno de los dos
jugadores tiene una estrategia ganadora, y explique cuál es.
X
Problema 5
Sea ABC un triángulo acutángulo, D un punto en el interior del lado BC talque DC = 2BD, la
medida del ángulo ∠ABD = 45◦ , la medida del ángulo ∠BAD = 15◦ . Sea E un punto sobre el
segmento AD talque ∠DBE = 30◦ . Encuentre la medida del ángulo ∠ACB.
2
XI Convocatoria Nacional
Academia Sabatina Jóvenes Talento
Nicaragua 2015
Nivel 3
Noveno y Décimo Grado
Problema 1
Sea ABCD un cuadrado y P un punto en el interior tales que los segmentos P A, P B y P C están
en proporción 1, 2 y 3 respectivamente. Encontrar la medida del ángulo ∠AP B.
D
C
P
A
B
Problema 2
Se tiene un tablero de 9 × 8 con un número en cada casilla, de modo que los números en cada fila y
en cada columna están en progresión aritmética y la suma de los números en las esquinas es 2015.
Determina la suma de todos los números en el tablero.
Problema 3
Una transacción consiste en invertir una cantidad entera positiva x de córdobas que le generará
luego de x dı́as 3x córdobas por la mañana de ese dı́a. Si Juan la mañana del dı́a 1 tiene 1 córdoba
y cada dı́a realiza una transacción, ¿cuál es la máxima cantidad de dinero que puede tener Juan
al final del dı́a 10? Describa la forma en que Juan debe hacer las transacciones.
Problema 4
Escribimos en la pizarra los números 1, 2, 3, . . . , 100. ¿Cuántos números hay que borrar como
mı́nimo, para que el producto de los números que queden escritos en la pizarra termine en 2?
Problema 5
En las tres casillas del reglón de arriba y en las tres de la columna de la izquierda de la cuadrı́cula
que se muestra se escriben al azar los números 1 o −1. Después se llenan los 9 cuadritos restantes
según la regla siguiente: en cada casilla se pone el producto del número que aparece justo arriba
con el que aparece justo a la izquierda. ¿De cuántas maneras distintas puede haber quedado la
cuadrı́cula de 4 × 4.
3