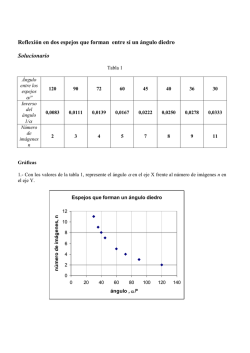
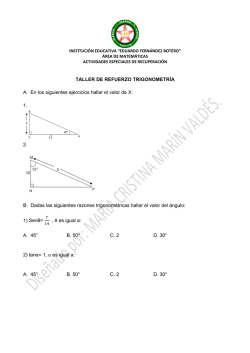
10-3 jm matematicas
INSTITUTO INTEGRADO DE COMERCIO TALLER HABILITACIÓN DE MATEMATICAS 10-3 J.M CLEOTILDE MATEUS MORALES SOLUCIONES UTILIZANDO RAZONES TRIGONOMETRICAS TEOREMA DE SENO Y COSENO. 1. Una torre inclinada 10º respecto de la vertical, está sujeta por un cable desde un punto P a 15 metros de la base de la torre. Si el ángulo de elevación del cable es de 25º, calcula la longitud del cable y la altura de la torre. 2) Una persona observa un avión y un barco desde la cúpula de un faro, tal como muestra la figura.¿Cuál es la distancia que hay del barco al avión y del barco al observador? 3) Un hombre mide un ángulo de elevación de una torre desde un punto situado a 100 metros de ella. Si el ángulo medido es de 20º y la torre forma un ángulo de 68º con el suelo, determina su altura AB. 4) Dos autos parten de una estación y siguen por carreteras distintas que forman entre si un ángulo de 80º. Si las velocidades son 60 km/h y 100 km/h, ¿qué distancia los separa después de una hora y media de recorrido? 5) Un árbol es observado desde dos puntos opuestos separados 250 metros con ángulos de elevación de 30º y 25º. ¿Cuál es la altura del árbol y a qué distancia está de la cúspide de cada punto de observación? 6) Mariana observa un castillo desde su casa bajo un ángulo de 70º. Luego de unos minutos sale a dar un paseo y estando a 50 metros de su casa, observa el mismo castillo bajo un ángulo de 85º. ¿A qué distancia de ella y de su casa, se encuentra dicho castillo? 7) Un árbol está situado en la orilla de un río. El extremo superior del árbol, desde un cierto punto (ubicado en la otra margen del río), determina un ángulo de elevación de 17º. Si a 25 metros de dicho punto y en dirección al árbol, el ángulo es de 35º, ¿cuál es la altura del mismo? 8) Tres pueblos X, W y Z, están unidos por carreteras rectas. La distancia entre X y W es de 6 km; a los pueblos W y Z los separan 9 km. El ángulo que forman las carreteras que unen X con W y W con Z es de 120º. ¿Qué distancia hay entre X y Z? 9) En una plazoleta de forma triangular, los lados miden 60 m, 75 m y 50 m. ¿Qué ángulos se forman en las esquinas de la misma? 10) Calcular la longitud de la diagonal AC del hexágono regular ABCDEF, si el perímetro del mismo es de 72 cm. SOLUCIONE LAS IDENTIDADE S 11. 12. 1 tan 2 x Csc2 x = Sec2x - 1 13. Sabiendo que tg α = 2, y que 180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α. 14. 15. 16. 17. SOLUCIONE LA ECUACION Cos2x- 2cosx - 3 = 0 18.Halla la distancia y ecuación canónica de la recta que pasa por A(2,0) y B(0,3) grafique 19. Halla la ecuación canónica de la recta que pasa por el punto y su pendiente es 20.Hallar una recta perpendicular a el punto A(3,5). Grafique. x + 2 y + 3 = 0, que pase por 21. Escriba la ecuación de la circunferencia de centro (4,6) y radio 5, realice la grafica 22. 23. Encuentre las coordenadas del vértice y foco, la ecuación eje de simetría y directriz , longitud de lado recto de la parábola de ecuación (x-3) 2 = 8 ( y-5) 2 realice el grafico 24. 25. Encontrar la ecuación de la elipse cuyo eje mayor esta sobre el eje x y tiene una magnitud de 10 F(3,8) y F (3,2), realice grafico. 26. Determinar los elementos de la hipérbola y su ecuación si tiene vértices (-3,2) y (-3,2) y la longitud de su lado conjugado es 6. 27. Realice A X B 3 -2 4 A 2 1 1 4 -1 0 1 -1 3 B 1 3 2 4 2 -2 28.Halle el determinante de B
© Copyright 2026