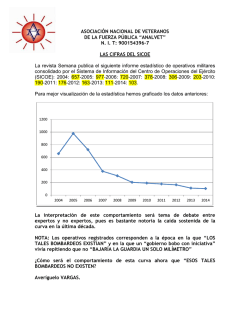
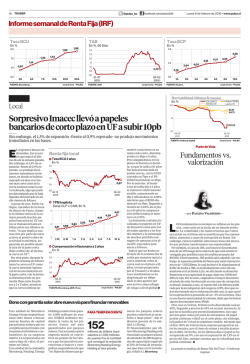
REPRESENTACIÓN GRÁFICA DE FUNCIONES
Apuntes de A. Cabañó.
Matemáticas II
REPRESENTACIÓN GRÁFICA DE FUNCIONES.
TEORÍA
- ESQUEMA A SEGUIR EN LA REPRESENTACIÓN DE FUNCIONES.
Para dibujar la curva (C) de la función f:x->y=f(x) se estudiará sucesivamente los siguientes puntos:
* Dominio (D) de la función o campo de existencia.
Conjunto de valores de x para los cuales existe f(x) y es real. Nos podremos encontrar los siguientes
casos:
a) Función polinómica: definida para todo valor real
b) Función racional: cociente de dos funciones polinómicas , existe para todo valor de x que no anule el
denominador.
c) Función irracional: y = n f(x)
- n impar: tiene el mismo dominio que f(x).
- n par: existe sólo para aquellos valores en los f(x) existe y es positiva o nula.
f(x)
existe en los puntos donde exista f(x).
d) Función exponencial: y = a
e) Función logarítmica: y = loga f(x) existe sólo para los valores de x que hacen f(x)>0.
f) Funciones seno y coseno: y = senf(x), y = cosf(x) existe para los mismos valores que f(x).
* Simetrías.
f(-x)=f(x)
Eje de simetría OY.
a) Función par:
f(-x)=-f(x)
Centro de simetría el origen.
b) Función impar:
Para comprobar que una curva no tiene simetrías (la función no es par ni impar) basta ver que, siendo a
un punto cualquiera del dominio d, se tiene que f(-a) ≠ f(a) y f(-a) ≠ -f(a) .
* Puntos de corte con los ejes.
a) Corte con el eje OX f(x)=0
b) Corte con el eje OY f(0)=y
Las abscisas de los puntos de corte son las raíces de esta ecuación.
* Asíntotas.
Se dice que una curva tiene ramas infinitas si existen puntos de la curva cuya distancia al origen de
coordenadas es mayor que cualquier número prefijado.
Si una curva tiene ramas infinitas, la recta (si existe) a la cual se aproxima la curva cada vez más sin
llegar a tocarla, se llama asíntota. Si la curva no tiene asíntotas, se dice que la curva tiene rama
parabólica.
a) Asíntota vertical o paralelas al eje OY.
Son de la forma x=u siendo u los valores finitos de x que hacen el siguiente límite ∞
lim f(x) = ±∞
x →u
(u = a, a+ , a- )
Es conveniente estudiar la posición de la curva respecto de la asíntota vertical, para ello se realizarán los
límites laterales
b) Asíntota horizontal o paralela al eje OX.
f(x) = k
Son de la forma y=k siendo k
lim
x → ±∞
Es muy conveniente estudiar la posición de la curva respecto de la asíntota, bastará hallar el signo de
f(x)-k para x->+∞ y x->-∞.
Si f(x)-k es positivo la curva estará por encima de la asíntota y si es negativo estará por debajo.
1
Representación gráfica de funciones
Apuntes de A. Cabañó.
Matemáticas II
c) Asíntota oblicua
f(x)
m, n ∈ ℜ
m = lim x
x → ±∞
Son de la forma y=mx+n
n = lim [f(x) - mx] m ≠ 0
x → ±∞
d) Ramas parabólicas.
Se estudian solamente si
lim f(x) = ∞
x →+∞
- Si
lim
x →∞
- Si
lim
x →∞
- Si
lim
x →∞
ó
lim f(x) = ∞
x →- ∞
f(x)
= ∞ la curva tiene una rama parabólica en la dirección del eje OY.
x
f(x)
= 0 la curva tiene una rama parabólica en la dirección del eje OX.
x
f(x)
= m ≠ 0 y lim [f(x) - mx] = ∞ la curva tiene una rama parabólica en la dirección de
x
x →∞
la recta y=mx
* Monotonía.
Para hallar los máximos y los mínimos se obtienen las raíces de la ecuación f'(x)=0, y los puntos en los
que no existe f'(x). Tendremos así los posibles puntos donde la función puede tener máximos y mínimos.
Dichos puntos son también los posibles extremos de los intervalos en los que la función es creciente o
decreciente.
Si a es una raíz de f'(x)=0, en el punto (a,f(a)) la curva tendrá un máximo o mínimo, o un punto de
inflexión con tangente horizontal según sea par o impar la primera derivada no nula de orden mayor o
igual que dos.
f'>0
a) Intervalos de crecimiento
f'<0
b) Intervalos de decrecimiento
c) Puntos críticos
MÍNIMO f'(a)=0 y f''(a)>0
MÁXIMO f'(a)=0 y f''(a)<0
Si f'(a)=0 , f''(a)=0 , f'''(a) ≠ 0 en a existirá un punto de inflexión con tangente horizontal.
(4
Si f'(a)=0 , f''(a)=0 , f'''(a)=0 en a existirá : MÁXIMO si f (a)<0
; MÍNIMO
(4
si f (a)>0
* Curvatura.
Un punto del dominio de definición de una función es punto de inflexión si la tangente a de la función en
este punto atraviesa a la curva.
a) Intervalo de convexidad f''<0
b) Intervalo de concavidad f''>0
pasa de CC-CV si f''(a)=0 y f'''(a)<0; pasa de CV-CC si f''(a)=0 y f'''(a)>0
c) Puntos de inflexión
Ejemplo
Haz la gráfica de la siguiente función:
f (x ) =
x2 + 2x − 2
x −1
• Dominio = R − {1}
• Simetrías:
x2 − 2x − 2
. No es par ni impar : no es simétrica respecto al eje Y ni
f (− x ) =
x2 + 2
respecto al origen.
• Asíntotas verticales:
2
Representación gráfica de funciones
lím f (x ) = − ∞
x = 1 es asíntota vertical
lím+ f (x ) = + ∞
x →1
Apuntes de A. Cabañó.
Matemáticas II
x →1−
1
x2 + 2 x − 2
= x +3+
→ y = x + 3 es asíntota oblicua
x −1
x −1
Posición de la curva respecto a la asíntota:
f (x) − (x +3) < 0 si x → − ∞ (curva por debajo).
f (x) − (x +3) > 0 si x → + ∞ (curva por encima).
• Puntos singulares. Crecimiento y decrecimiento:
• Asíntota oblicua: y =
f ' (x ) =
( 2 x + 2) ( x − 1) − ( x 2 + 2 x − 2) 2 x 2 − 2 x + 2 x − 2 − x 2 − 2 x + 2 x 2 − 2 x
=
=
( x − 1) 2
( x − 1) 2
( x − 1) 2
x = 0
f ' (x ) = 0 → x 2 − 2 x = 0 → x ( x − 2) = 0 →
x = 2
Puntos (0, 2) y (2, 6).
Signo de f ' (x):
f (x) es creciente en (−∞, 0) ∪ (2, +∞); es decreciente en (0, 1) ) ∪ (1, 2). Tiene un
máximo en (0, 2) y un mínimo en (2, 6).
Corte
con
los ejes:
•
Con el eje Y → x = 0 → y = 2 → Punto (0, 2)
− 2 ± 4 + 8 x ≈ −2,73
- Con el eje X → y = 0 → x 2 + 2 x − 2 = 0 → x =
2
x ≈ 0,73
Puntos: (−2,73; 0); (0,73; 0)
• Gráfica:
Ejemplo
ex
x −1
• Dominio = R − {1}
• Asíntotas:
lím f (x ) = −∞
x →1−
x = 1 es asíntota vertical.
lím+ f (x ) = +∞
x →1
Representa: f (x ) =
e− x
= 0 y = 0 es asíntota horizontal si x → −∞ (f (x) < 0)
x → −∞
x → +∞ − x − 1
f (x )
= +∞ → Rama parabólica
lím f (x ) = +∞ , lím
x → +∞
x → +∞
x
• Puntos singulares. Crecimiento y decrecimiento:
lím f (x ) = lím
3
Representación gráfica de funciones
Apuntes de A. Cabañó.
Matemáticas II
f ' (x ) =
e x ( x − 1) − e x e x ( x − 2)
=
( x − 1) 2
( x − 1) 2
f ' (x) = 0 → ex(x − 2) = 0 → x = 2
Signo de f ' (x):
f (x) es decreciente en (−∞, 1) ∪ (1, 2); es creciente en (2, +∞). Tiene un mínimo en
(2, e2).
• Corta al eje Y en (0, −1). No corta al eje X.
• Gráfica:
Ejemplo
Representa gráficamente: f (x ) =
1
2
x −1
• Dominio = (−∞, −1) ∪ (1, +∞)
• Simetrías:
f (−x) = f (x). Es par: simétrica respecto al eje Y.
• Asíntotas:
lím − f (x ) = +∞ → x = −1 es asíntota vertical
x → −1
lím f (x ) = +∞ → x = 1 es asíntota vertical
x →1+
lím f (x ) = lím f (x ) = 0
x → −∞
x → +∞
y = 0 es asíntota horizontal (f (x) > 0 para toda x)
• Puntos singulares. Crecimiento y decrecimiento:
−1
−3
1
−x
f (x ) = x 2 − 1 2
f ' (x ) = − x 2 − 1 2 · 2 x =
2
( x 2 − 1)3
(
)
(
)
f ' (x) = 0 → x = 0 (no vale)
f (x) no tiene puntos singulares (en x = 0 no está definida)
Signo de f ' (x):
f (x) es creciente en (−∞, −1); y es decreciente en (1, +∞).
• f (x) no corta a los ejes.
• Gráfica:
4
Representación gráfica de funciones
Apuntes de A. Cabañó.
Matemáticas II
PROBLEMAS SOBRE MÁXIMOS Y MÍNIMOS.
Pasos a seguir:
- Mediante los datos del problema se construye la función que hay que maximizar o minimizar.
- Si la función tiene más de una variable hay que relacionar las variables mediante ecuaciones a fin de
conseguir expresar la función inicial utilizando una sola variable.
- Se hallan los extremos de esta función.
- Se interpretan los resultados obtenidos rechazando aquellos que por la naturaleza del problema no
sean posibles.
Ejemplo
Una huerta tiene actualmente 24 árboles, que producen 600 frutos cada uno. Se calcula que, por
cada árbol adicional plantado, la producción de cada árbol disminuye en 15 frutos. ¿Cuál debe ser el
número total de árboles que debe tener la huerta para que la producción sea máxima? ¿Cuál será
esa producción?
Llamamos x al número de árboles que se plantan. Tenemos que el número de frutos sería:
f (x) = (24 + x) (600 − 15x) = −15x2 + 240x +14 400
Buscamos x para que f (x) sea máxima:
240
=8 → x=8
f ' (x) = −30x + 240 f ' (x ) = 0 → − 30 x + 240 = 0 → x =
30
Veamos que es un máximo:
f '' (x) = −30 ; f '' (8) = −30 < 0 → en x = 8 hay máximo. (Como f (x) corresponde a una
parabola invertida, en x = 8 está el máximo absoluto).
Por tanto, se deben plantar 8 árboles. Así, habrá un total de 24 + 8 = 32 árboles, que
producirán 15 360 frutos.
REPRESENTACIÓN GRÁFICA DE FUNCIONES.
PROBLEMAS.
3
2
1º- Dada la función f(x)=x -5x +3x-1 se pide: máximos y mínimos; intervalos de crecimiento y
decrecimiento; intervalos de concavidad y convexidad.
3
2
2º- Hallar la ecuación de la recta tangente a la curva f(x)=x -6x +16x-11 en su punto de inflexión.
3º- Hallar los máximos, mínimos y puntos de inflexión de las siguientes funciones:
2
-x
3.1 y = x ⋅ e
2
3.2 y =
2
3.3 y = x + ln( x - 1)
3x - 5 x 2
4º-Hallar los máximos y los mínimos de las funciones:
2
x
4.2 y = x ⋅ e
2
4.1 y =| x - 2x |
3
2
5º-Calcular los coeficientes del polinomio p(x) = ax + bx + cx + d sabiendo que para x=-1 tiene un
máximo relativo de 11 unidades, que para x=5 tiene un mínimo y la función pasa por el punto (1,-17).
5
Representación gráfica de funciones
Apuntes de A. Cabañó.
Matemáticas II
3
2
6º-Hallar a y b de modo que la función f(x) = x - ax - 4x + b corte al eje OX en x=3 y tenga un punto
de inflexión en x=2/3.
-n
7º-Hallar los máximos y mínimos de f(x) = x ⋅ lnx
con n perteneciente a los naturales.
8º-Razona si es cierta o falsa la siguiente afirmación: "Toda función polinómica de grado tres tiene
siempre un punto de inflexión"
9º-Representar gráficamente las funciones:
3
9.1 y =
x
(1 + x )2
9.4 f ( x ) =
x2 −1
x
9.2 y = ±
x+2
x
9.5) f ( x ) =
x
x −1
9.3 f ( x ) =
x3
x2 −1
2
10º-Determinar las dimensiones que hacen mínima la superficie de un ortoedro si su volumen es 72 cc. y
la razón de dos de sus dimensiones es 1/2.
11º-Se desea construir un embudo cónico de generatriz 20 cm. Determinar la altura del embudo de modo
que sea máximo el volumen.
DATO: V =
π 2
R ⋅h
3
12º-Determinar cuales deben ser las dimensiones de una vasija de forma cilíndrica de 2 cc de volumen
de modo que sea mínima la cantidad de material empleada en su construcción.
2
DATO: V = π R h
2
13º-La parte escrita ocupa 400 cm de la página de un libro, los márgenes superior e inferior deben ser
de 2 cm. y los márgenes laterales de 3 cm. ¿Cuáles deben ser las dimensiones de la página para
obtener mayor economía en el papel?.
14º-En un cono de base circular de radio R y de altura H se inscribe otro cono de volumen máximo, base
paralela a la suya y con el vértice en el centro de la misma. Hallar el volumen de este segundo cono.
15º-Se considera una ventana rectangular tal que el lado superior ha sido construido en forma de
triángulo equilátero. Sabiendo que el perímetro de la ventana es de 4,5 m. hallar sus dimensiones para
que su área sea máxima.
16º-Desde una casa situada en el punto P=(7,0) se quiere hacer un camino recto para conectarla con
una carretera cuyo trazado viene dado por la curva de ecuación y =
la carretera conecta el camino más corto posible?
1 + 2x + 2 x 2 ¿Con qué punto de
17º-De todas las rectas que pasan por el punto (1,2) encuentra la que determina con los ejes
coordenados y el primer cuadrante un triángulo de área mínima y el valor de dicha área.
3
2
18º- Dada la función y = ax + bx + cx + d hallar los coeficientes a, b, c, d, sabiendo que la ecuación
de la tangente a la curva en el punto de inflexión (1,0) es y=-3x+3 y que la función presenta un extremo
en el punto de abscisa x=0.
19º-Estudiar la monotonía de las siguientes funciones:
6
Representación gráfica de funciones
Apuntes de A. Cabañó.
Matemáticas II
2
a) f(x) = x ⋅ ln x
2
b) f(x) = x ⋅ lnx
20º- Hallar los máximos, mínimos y puntos de inflexión de la función f ( x ) = x (1 − x )
4
3
PROBLEMAS RESUELTOS.2
1º-Dada la función y =
x +x-5
se pide:
x-2
a) Obtener las dos asíntotas de esta curva.
b) Localizar los máximos y mínimos de la función.
c) Obtener los puntos de intersección con los ejes coordenados.
d) Dibujar la gráfica.
Sol: a) A.O y=x+3 ; A.V. x=2
b) M(1,3) m(3,7)
c) P.C. OY: (0,5/2) ; P.C. OX: (-2'8,0) (1'8,0)
2º-Determina el punto de la curva cuya ecuación es y=x² que está más cerca del punto A=(3,0).
Sol:(1,1)
3º-Encontrar los máximos y mínimos relativos de: f(x) = x +
1
x
2
3
Sol: m( 2 ,1'89)
-n
n
4º-Hallar los extremos relativos de f(x) = x ln x donde n es par. Sol: ( e ,
n
n
)
n 1 Max n>0 min n<0
e
3
2
5º-Calcúlense las ecuaciones de las tangentes a la curva y = 4 x - 2 x - 10 en los puntos de inflexión y
de máximo o mínimo relativo.
Sol: y=-10 y+271/27=-1/3(x-1/6) y=-272/27
6º-En una carrera a través del desierto un automóvil debe ir desde la ciudad A hasta el oasis P situado a
500 km de distancia de A. Puede aprovechar para ello una carretera recta que une las ciudades A y B y
que le permite ir a una velocidad de 100 km/h mientras que por el desierto la velocidad es de 60 km/h.
Sabiendo que la distancia más corta de P a la carretera que une las ciudades A y B es de 300 km,
determinar la ruta que deberá usar para ir de A a P en el menor tiempo posible. Sol: d=175
7º-Se desea construir una lata de conservas en forma cilíndrica circular recta de área total 150
centímetros cuadrados y el volumen máximo. Determinar su generatriz y su radio.
8º-Representar gráficamente la función: y =
Sol: h =
10
π
x
calculando dominio de definición, extremos,
x - 5x + 4
2
intervalos de crecimiento y decrecimiento, asíntotas y puntos de corte con los ejes.
Sol: Dom=R-{1,4}
A.V.; x=1 x=4
A.H.; y=0 P.C.(0,0)
m(-2,-1/9) M(2,-1)
9º-Con una chapa de hojalata cuadrada de lado 60 cm. es preciso hacer un cajón sin tapa que tenga
volumen máximo. Se recortan cuadrados en los ángulos de la hojalata y se dobla esta para formar el
cajón ¿Cual debe ser la longitud del lado de los cuadrados recortados?. Sol: l=10
10º-De todos los conos inscritos en una esfera de radio 4 m, determinar la altura y radio de la base del
que tiene máximo su volumen.
7
Representación gráfica de funciones
Sol: h =
16
;
3
r=
Apuntes de A. Cabañó.
Matemáticas II
8
2
3
11º-Representar gráficamente las funciones:
a) f(x) =
3x
1 − x2
b) f(x) =
3
2 x3
2
x +1
2
12º-Dada la función y = ax + bx + cx + d hallar los coeficientes a, b, c, d, sabiendo que la ecuación
de la tangente a la curva en el punto (1,1) es y=-x+2 y que la función presenta un extremo en el punto
(0,2).
Sol: a=2 b=-2 c=0 d=2
13º-Estudiar la curvatura de las siguientes funciones:
2
a) f(x) = x ⋅ ln x
2
b) f(x) = x ⋅ lnx
c) f ( x ) =
ln x
x
14.- La suma de los catetos de un triángulo rectángulo es 40 cm. Halla sus dimensiones para que la
superficie de ese rectángulo sea máxima. Sol: Dos catetos iguales de 20 cm
15.- Se quieren fabricar latas de refresco (cilíndricas) cuyo contenido sea de 1/3 de litro, de manera que
el coste de la chapa sea mínimo; halla su altura y radio de la base. Mide las dimensiones de cualquier
lata que tengas en casa y comprueba si se fabrican siguiendo ese criterio.
Sol: R =
3
36
1
dm h = 3
27 π
6 π
16.- Un comerciante vende mensualmente 3000 latas de refresco a un precio de 60 céntimos/lata y sabe
que por cada céntimo que rebaja en el precio vende 150 latas más, de la misma forma si aumenta el
precio 1 céntimo vende 150 latas menos. Si al comerciante le cuesta cada lata 30 céntimos. ¿A qué
precio ha de vender las latas para obtener el máximo beneficio?. Sol: 55 céntimos
2
17.- Queremos vallar una parcela rectangular de 200 m de una finca aprovechando un muro ya
existente, de modo que en ese lado no es necesaria valla. ¿Cómo debe ser ese rectángulo para que el
coste de la valla sea mínimo?. Sol: 10H20
18.- Un jardinero quiere construir un parterre con forma de sector circular. Lo quiere rodear con una valla.
Si sólo dispone de 40 m, ¿cuál será el radio para que la superficie sea máxima?. Sol: r=10m
19.- Se quiere vallar una parcela rectangular junto a una carretera. Si la valla junto a la carretera cuesta 1
euro/m y el resto 50 céntimos/m. ¿Cuáles serán las dimensiones de la parcela para que el área sea
máxima si disponemos de 180 euros?. Sol: 60H90 m.
20.- Hallar las dimensiones de un rectángulo de área máxima inscrito en una circunferencia de radio 2.
Sol: x=√8, y=√8
21.- De todos los triángulos isósceles de perímetro 9. Hallar las dimensiones del que tenga área máxima.
Sol: x=3, y=3
8
Representación gráfica de funciones
© Copyright 2026