1. No category

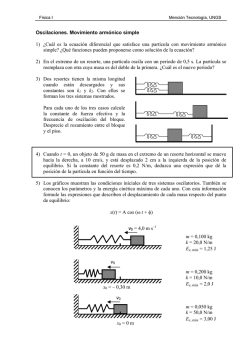
FÍSICA
2º BACHILLERATO
Problemas sobre “Vibraciones”
1) Responda los siguientes apartados:
a) Un cuerpo de masa m, unido a un resorte horizontal de masa
despreciable, oscila con un movimiento armónico simple. Si su energía
mecánica es E, analice las variaciones de energía cinética y potencial
durante una oscilación completa.
b) Si el cuerpo se sustituye por otro de masa m/2, ¿qué le ocurre al período
de oscilación? Razone la respuesta.
2) Responda los siguientes apartados:
a) Explique las variaciones energéticas que se dan en un oscilador
armónico durante una oscilación. ¿Se conserva la energía del oscilador?
Razone la respuesta.
b) Si se duplica la energía mecánica de un oscilador armónico ¿cómo varía
la amplitud y la frecuencia de las oscilaciones? Razone la respuesta.
3) Un resorte vertical se alarga 2 cm cuando se cuelga de su extremo inferior
un cuerpo de 10 Kg. Se desplaza dicho cuerpo hacia abajo y se suelta, de
forma que el sistema comienza a oscilar con una amplitud de 3 cm.
a) Calcule la constante recuperadora del resorte y el período del
movimiento. (5000 N/m) (0,28s)
b) Haga un análisis de las transformaciones energéticas que tienen lugar
en una oscilación completa y calcule el valor de las energías cinética y
potencial elástica cuando el desplazamiento es 1,3 cm. (1,83 J) (0,42 J)
Dato: g = 10 m s-2
4) Se hace oscilar desde la posición de equilibrio un cuerpo unido a un muelle
horizontal, de modo que la separación máxima de dicha posición es de 3
cm. Si se han contado 20 oscilaciones en 5 segundos, ¿cual es la ecuación
representativa de dicho movimiento?
5) Un cuerpo unido a un muelle comienza a oscilar horizontalmente desde su
posición extrema, a 4 cm de la posición de equilibrio, con un período de 0,3
s. Calcula:
a) Su velocidad al pasar por la posición de equilibrio. (±0,838 m/s)
b) Su velocidad cuando x = 2 cm. (±0,726 m/s)
6) Consideremos la velocidad y la aceleración máximas de un oscilador:
a) ¿Cómo varían si se duplica la amplitud sin modificar el período?
b) ¿Cómo varían si se duplica la frecuencia sin modificar la amplitud?
MCANTO 02/12
www.miguelcanto.eu
Página 1
7) Un cuerpo de 1,4 Kg de masa se conecta a un muelle de constante elástica
15 N/m, y el sistema oscila horizontalmente. La amplitud del movimiento es
de 2,0 cm. Calcula:
a) La energía total del sistema. (0,003 J)
b) Las energías cinética y potencial cuando el desplazamiento del cuerpo
es de 1,3 cm. (1,73 10-3 J) (1,27 10-3 J)
c) La velocidad máxima del cuerpo. (0,065 m/s)
8) Una partícula que describe un movimiento armónico simple (m.a.s.) de
amplitud A = 10 cm, vibra en el instante inicial con su máxima velocidad de
10 m ⋅ s-1.
a) Halla la frecuencia de la oscilación. (15,92 Hz)
b) Halla la aceleración máxima y la mínima del m.a.s. (103 m/s2) ( 0 m/s2)
c) Determina la posición, velocidad y aceleración de la partícula en el
instante t = 1 s. (-0,0506 m) (8,623 m/s) (506 m/s2)
9) Una partícula de masa m = 10 g oscila armónicamente en torno al origen
de un eje OX, con una frecuencia de 5 Hz y una amplitud de 5 cm.
a) Calcule la velocidad de la partícula cuando pasa por el origen. (1,57
m/s)
b) Determine y represente gráficamente la energía cinética de m en función
del tiempo. Tome origen de tiempo, t = 0, cuando m pasa por x = 0.
10) Responda los siguientes apartados:
a) Demuestre que en un oscilador armónico simple la aceleración es
proporcional al desplazamiento pero de sentido contrario.
b) Una partícula realiza un movimiento armónico simple sobre el eje OX y
en el instante inicial pasa por la posición de equilibrio. Escriba la
ecuación del movimiento y razone cuándo es máxima la aceleración.
MCANTO 02/12
www.miguelcanto.eu
Página 2