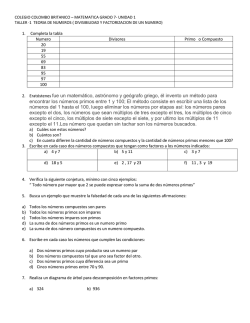
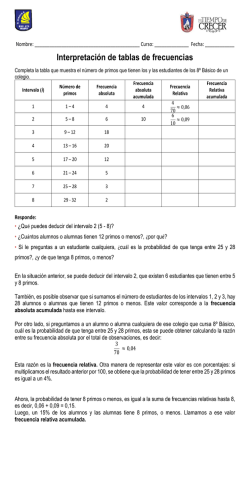
Divisores 1. Escribe el conjunto de todos los
Institución Educativa Dinamarca Plan de Apoyo 2015 Área: Matemáticas Período: 3 Grado: 6°D Docente: Brigitt Hernández Nombre del estudiante: ______________________________________________________________________________ Etapa No 1 Actividad Entrega de taller 2 Entrega resuelto de 3 Sustentación taller Plan de acción Fecha de Forma de entrega entrega Septiembre 16 Virtual, a través de la página institucional Lugar de entrega Página web Septiembre 24 Físico en carpeta legajadora Durante la clase Septiembre 24 Evaluación escrita Durante la clase Esta actividad de recuperación la debe realizar de la siguiente manera Resolver cada uno de los problemas planteados. No debe hacer desarrollo, debe copiar las preguntas e irlas respondiendo Las preguntas las debe copiar y responderlas en hojas de block tamaño carta, a mano, en letra legible, con buena ortografía y legajado (no grapado) en carpeta de cartón carta, con portada. Entregar el día asignado e impecablemente presentado. Divisores 1. Escribe el conjunto de todos los divisores de cada número a. 8 b. 6 c. 7 d. 9 e. 10 g. 14 h. 15 i. 24 j. 30 k. 42 2. Completa con las palabras múltiplo o divisor para que sean verdaderas f. 12 l. 70 a. 35 es ________________ de 5 g. 12 es ________________ de 36 b. 24 es ________________ de 8 h. 8 es ________________ de 32 c. 15 es ________________ de 30 i. 9 es ________________ de 36 d. 10 es ________________ de 5 j. 5 es ________________ de 10 e. 6 es ________________ de 36 k. 4 es ________________ de 20 f. 12 es ________________ de 60 l. 20 es ________________ de 4 3. Determina para las siguientes afirmaciones cuales son verdaderas o falsas a. Cero es divisor de todo número. ___________ b. Todo número es divisor de sí mismo ___________ c. El conjunto de divisores de un número es infinito ___________ d. Todo número es divisible entre 1 ___________ e. Un número divisible entre 5 también es divisible entre 3 ___________ 4. Lee la siguiente información Un número es perfecto si es igual a la suma de sus divisores, excluyendo el propio número. Comprueba que los siguientes números son perfectos. a. 6 b. 28 c. 496 d. 8.128 5. Determina si los siguientes números son divisibles entre tres: a. 50 c. 121 e. 47 b. 60 d. 37 f. 1210 6. Halla los divisores de cada uno de los siguientes números. Luego, determina cuáles números son primos y cuales son compuestos. a. 18 b. 47 c. 25 d. 32 e. 143 f. 250 g. 12 h. 450 i. 1230 7. Escribe un número que cumpla cada condición a. Compuesto y par d. Primo par b. Primo impar e. Primo que termine en 3 c. Compuesto impar 8. Los números primos gemelos son aquellos que tienen como diferencia 2. Por ejemplo, 3 y 5 son primos gemelos, ya que 5 − 3 = 2 Encuentra tres pares de números primos que sean gemelos. Factorizar un número significa expresar dicho número como un producto de factores primos. 9. Factorizar los siguientes números a. 18 b. b. 84 10. Lee el texto Los números primos han despertado el interés de los matemáticos desde la antigüedad y han tenido gran importancia tanto en las matemáticas como en sus aplicaciones. Uno de los resultados más importantes asociados a los números primos es el teorema fundamental de la aritmética que afirma: todo número natural es primo o puede expresarse como el producto de números primos. a. Escribe la idea principal del texto. b. Responde ¿todos los números naturales cumplen este teorema? 11. Daniel quiere descomponer un número en factores primos. Y lo hace de la siguiente forma: Responde: 60 2 30 2 a. ¿El producto 2 𝑥 2𝑥 15 es igual a 60? b. ¿Cuál es el error que cometió Daniel en la descomposición? 15 15 1 12. Realiza la descomposición en factores primos de los siguientes números naturales. a. 32 d. 3.900 g. 1.234 b. 249 e. 1.500 h. 5.600 c. 1000 f. 3.600 i. 7.200 Mínimo común múltiplo 1. Hallar el mdc de los siguientes números. a. Mcd (16, 12, 36) e. Mcd (18, 35, 40) b. Mcd (48, 36) f. Mcd (100, 75, 50) c. Mcd (8, 16, 10) g. Mcd (16, 24) d. Mcd (21, 12, 36) h. Mcd (45, 50) 2. Soluciona los siguientes problemas a. En una floristería hay 100 rosas rojas y 72 rosas amarillas, para elaborar ramos. Si cada ramo debe tener la misma cantidad de rosas, ¿de cada color que debe tener cada ramo? b. Juan tiene que poner un guarda escobas de madera a dos paredes de 12 m y 9 m de longitud. Para ello, averiguó la mayor longitud del listón de madera que cabe en un número exacto de veces en cada pared ¿Cuál es la longitud del listón? c. Marta tiene un rollo de cinta verde 90 m y un rollo de cinta roja de 120 m, ¿cuántos metros de cinta debe usar para cada moño, si quiere que todas las cintas sean de la misma longitud y no sobre cinta? d. En la siguiente tabla se registró el número de niños y niñas que hay por grado en un colegio. Sexto Séptimo Octavo Noveno Décimo Once Niños 16 25 24 18 32 40 Niñas 40 20 18 30 20 16 Si para cada grupo se requiere formar grupos con igual cantidad de integrantes, de manera que en cada grupo la cantidad de niños y niñas sea la misma ¿Cuál es la mayor cantidad de grupos que se pueden armar por grado? Resuelve los siguientes problemas usando el mínimo común múltiplo 3. Luisa debido a su enfermedad visitó al médico y éste le indicó aplicarse una inyección cada 18 horas, tomar una cucharada de jarabe cada 12 horas y tomarse una pastilla cada 8 horas. Si acaba de tomar los tres medicamentos a la vez. a. Cuántas horas pasaran para que nuevamente vuelva a suministrarse los tres medicamentos al tiempo. b. Durante las horas que pasan para que nuevamente se suministre los tres medicamentos al tiempo, se ha tomado un total de: 4. David, Sendy y Sophia visitan a su abuela, pero lo hacen en tiempos diferentes, David va cada 9 días, Sendy va cada 12 días y Sophia va cada 15 días. a. Si hoy están los tres en casa de la abuela, cuantos días pasarán para que se vuelvan a encontrar en la casa de la abuela. b. Las veces que David y Sophia visitan a su abuela en el tiempo que transcurre para que se encuentre nuevamente los tres son
© Copyright 2026