Download Report

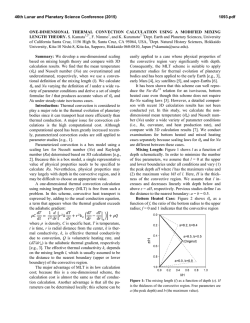
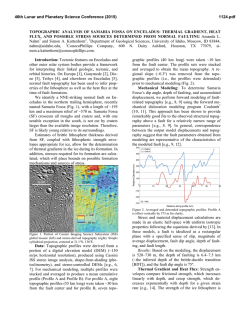
46th Lunar and Planetary Science Conference (2015)
1573.pdf
A SIMPLE ONE-DIMENSIONAL RADIATIVE-CONVECTIVE ATMOSPHERE MODEL FOR USE
WITH EXTRASOLAR ATMOSPHERES. R. L. Mickol1, H. N. Farris1, E. Kohler1, V. Chevrier1, T. A. Kral1,2
and C. Lacy1,3. 1Arkansas Center for Space and Planetary Sciences, University of Arkansas, Fayetteville, AR, 72701,
USA; 2Dept. of Biological Sciences, University of Arkansas, Fayetteville, Arkansas, 72701, USA; 3Dept. of Physics,
University of Arkansas, Fayetteville, Arkansas, 72701, USA; [[email protected]].
Introduction: Since the discovery of the first extrasolar planet over 20 years ago [1], there currently
exist over 1750 confirmed planets outside our solar
system [2]. As technology has advanced over the last
few years, it is now possible to determine the major
constituents of exoplanet atmospheres [3-5]. To learn
more about these planetary systems, an accurate atmospheric model is needed.
This project aims to reproduce a radiativeconvective model written by Robinson and Catling
(2012) [6]. The model will be transferred from the
programming language IDL, to Python, which is freely
available, in an effort to make the code easier to use
and obtain. In addition, following successful reproduction of the model, we will attempt to model the formation of unusual cloud types in exoplanet atmospheres.
This project serves to improve the initial model presented previously [7].
Methods: The radiative-convective model of
Robinson and Catling [6] was copied from IDL into
Python, accounting for differences in syntax.
This model uses ten input parameters (see Table 1)
and outputs two variables, τ0 (gray infrared optical
depth integrated from top of atmosphere down to p0)
and τrc (optical depth at boundary between convective
and radiative regions), in a solution [6]. In the radiative
region ( 0 ≤ τ ≤ τrc), the temperature, upwelling thermal
flux and downwelling thermal flux are given by equations 1, 2, and 3, respectively:
(1)
where Fi is the internal flux of the planet (Fi,Titan = 0)
and D is the diffusivity factor (D = 1.66) [6]. The temperature, upwelling thermal flux and downwelling
thermal flux in the convective region ( τrc ≤ τ ≤ τ0), are
given by equations 4, 5, and 6, respectively:
(4)
(5)
(6)
where β = α(γ - 1)/γ.
Table 1. Model Input Parameters [6]
Parameter
Titan
Jupiter
1.5 bar
1.1 bar
94 K
191 K
4/3
2
ratio of specific heats
at constant P, V
1.4
1.4
α
avg. ratio of true lapse
rate (convection region) to dry adiabatic
lapse rate
0.77
0.85
F1s
absorbed stellar flux in
channel 1
1.5
W/m2
1.3
W/m2
F2s
absorbed stellar flux in
channel 2
1.1
W/m2
7.0
W/m2
k1
ratio of visible optical
depth to gray infrared
optical depth (Ch. 1)
114
163.6
k2
ratio of visible optical
depth to gray infrared
optical depth (Ch. 2)
0.2
0.03
reference pressure
T0
reference temperature
n
scaling parameter
γ
(2)
(3)
Definition
p0
Additionally, working with our initial model [7] reproducing the simple one-dimensional radiative model
from Robinson and Catling [6], we have determined
additional vapor pressure curves to apply to extrasolar
planet atmospheres. Curves for forsterite (Mg2SiO4),
46th Lunar and Planetary Science Conference (2015)
sodium sulfide (Na2S), and aluminum oxide (Al2O3)
were obtained from Fortney (2005) [8]. Curves for
enstatite (MgSiO3) and iron (Fe) were reproduced using the vapor pressure equations from Ackerman and
Marley (2001) [9]. However, a correction of 0.5 x 105
was required to produce the accurate curve (verified
using Fortney [2005]). Model parameters for exoplanet
GJ3470b were obtained from the NASA Exoplanet
Archive [2].
Results: Following the example provided by Robinson and Catling, the thermal profile of Titan was
successfully reproduced (Fig. 1). Further, using the
designated input parameters [6], the thermal profile of
Jupiter was also produced (Fig. 2).
Vapor pressures of five elements and compounds
(Mg2SiO4, Na2S, Al2O3, MgSiO3 and Fe) were graphed
against the thermal profile for GJ3470b (Fig. 3).
1573.pdf
solar flux, and the convective flux [6]. The model will
also be adapted to be used with the NASA Exoplanet
Archive in order to model exoplanet atmospheres.
Five vapor pressure curves were plotted for the
thermal profile of exoplanet GJ3470b using our initial
simple radiative atmospheric model [7]. Clouds can
potentially form where the compound/element saturation vapor pressure curve intersects the thermal profile
of the exoplanet (Fig. 3). Future work will address
additional compounds that could be present in
exoplanet atmospheres. We will also model additional
exoplanets in the attempt to constrain possible cloud
types/heights with model parameters.
Figure 3. Thermal profile of exoplanet GJ3470b (red,
solid curve), using model previously described [7].
Vapor pressure curves (dotted) for various elements
and compounds are labeled (obtained from [8, 9]).
Figure 1. Thermal profile of Titan.
Figure 2. Thermal profile of Jupiter.
Discussion/Conclusion: The simple radiativeconvective atmospheric model of Robinson and Catling [6] was successfully reproduced in Python for the
examples of Titan (Fig. 1) and Jupiter (Fig. 2). Future
work will enhance the model with the addition of the
upwelling and downwelling thermal fluxes, the net
Acknowledgements: The authors would like to
acknowledge T. D. Robinson and D. C. Catling for the
availability and usefulness of their code. This research
has made use of the NASA Exoplanet Archive, which
is operated by Caltech, under contract with NASA
under the Exoplanet Exploration Program.
References: [1] Wolszczan, A. and Frail, D. A.
(1992) Nature, 355, 145-147. [2] NASA and Caltech.
NASA
Exoplanet
Archive.
(2014)
http://exoplanetarchive.ipac.caltech.edu/. [3] Tinetti,
G. et al. (2007) Nature, 448, 169-171. [4] Swain, M.
R., Vasisht, G. and Tinetti, G. (2008) Nature, 452,
329-331. [5] Fraine, J. et al. (2014) Nature, 513, 526529. [6] Robinson, T. and Catling, D. (2012) The Astrophys. J., 757, 104 (13pp). [7] Kohler, E., et al.
(2014) LPS XLV, Abstract #2290. [8] Fortney, J. J.
(2005) Mon. Not. R. Astron. Soc., 364, 649-653. [9]
Ackerman, A. S. and Marley, M. S. (2001) The Astrophys. J., 556, 872-884.