1. No category

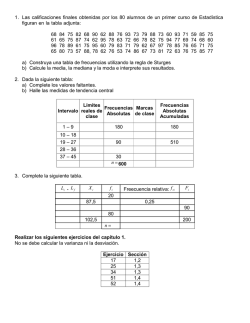
UNIVERSIDAD JOSE CARLOS MARIATEGUI
ESTADISTICA NO PARAMETRICA
LECCIÓN Nº 09
DISTRIBUCIONES JI-CUADRADO
9.1. DEFINICION.Antes de entrar en la estimacion de parametros por el metodo de intervalos de
confianza son necesarias algunas distribuciones importantes que vamos a enunciar.
Una propiedad importante de la distribuion es que esta tiende a la distribucion normal
cuando el numero de grados de libertad tiende a
La Distribución Ji cuadrada tiene por objeto comparar la media de una muestra
hipotética de una población, en un muestreo pequeño. Se utiliza para comprara la
varianza de una muestra con la varianza Hipotética de una población. Se denota con
la letra griega X(Ji) elevada al cuadrado. Este método corresponde al campo de la
estadística paramétrica. Igual que la distribución t depende del numero de grados de
libertad asociados al problema.
9.2. PRUEBA DE BONDAD DE AJUSTE
Consiste en probar la hipotesisi nula que cierta funcion F(x) es la funcion de
distribución de una población a partir de una muestra tomada de ella, o, consiste en
probar que los datos muestrale se distribuyen como F un metodo usual consiste en
verificar la concordancia entre las frecuencias observadas(0i) y las frecuencias
esperadas (ei), usando la prueba de bondad de ajuste X2(chi – Cuadrado) propuesta
por Kart Pearson.
Un experimento multinomial es la generalización de un experimento binomial:
1. Consiste en n pruebas idénticas e independientes.
EDUCA INTERACTIVA
Pág. 36
UNIVERSIDAD JOSE CARLOS MARIATEGUI
2. Para cada prueba, hay un número k de resultados posibles.
3. Cada uno de los k posibles resultados tiene una probabilidad de ocurrencia pi
asociada (p1 + p2 + ... + pk = 1), la cual permanece constante durante el desarrollo del
experimento.
4. El experimento dará lugar a un conjunto de frecuencias observadas (O1, O2, ..., Ok)
para cada resultado. Obviamente, O1 + O2 + ... + Ok = n.
En ocasiones estaremos interesados en comparar los resultados obtenidos al realizar
un experimento multinomial con los resultados esperados (teóricos). Ello nos permitirá
saber si nuestro modelo teórico se ajusta bien o no a las observaciones. Para ello,
recurriremos a la distribución Chi-cuadrado, la cual nos permitirá realizar un
contraste sobre la bondad del ajuste.
Concretamente, usaremos el estadístico
con k – 1 grados de libertad.
Donde:
Oi = frecuencia observada en la i-esima celda
Ei = frecuencia esperada en la i-esima celda si Ho es cierta
k = numero de celdas
Podemos calcular cada frecuencia esperada (teórica) multiplicando el número total de
pruebas n por la probabilidad de ocurrencia asociada, es decir:
Notas:
(1) El valor del estadístico χ2* se podrá aproximar por una distribución Chi-cuadrado
cuando el tamaño muestral n sea grande (n > 30), y todas las frecuencias esperadas
sean iguales o mayores a 5 (en ocasiones deberemos agrupar varias categorías a fin
de que se cumpla este requisito).
(2) Las observaciones son obtenidas mediante muestreo aleatorio a partir de una
población particionada en categorías.
EJEMPLO:
En cierta máquina Expendedora de Refrescos existen 4 canales que expiden el
mismo tipo de bebida.
Estamos interesados en averiguar si la elección de cualquiera de estos canales se
hace de forma aleatoria o por el contrario existe algún tipo de preferencia en la
selección de alguno de ellos por los consumidores. La siguiente tabla muestra el
número de bebidas vendidas en cada uno de los 4 canales durante una semana.
Pág. 37
EDUCA INTERACTIVA
UNIVERSIDAD JOSE CARLOS MARIATEGUI
Contrastar la hipótesis de que los canales son seleccionados al azar a un nivel de
significación del 5%.
SOLUCIÓN:
Para realizar el contraste de Bondad de Ajuste debemos calcular las frecuencias
esperadas de cada suceso bajo la hipótesis de uniformidad entre los valores. Si la
selección del canal fuera aleatoria, todos los canales tendrían la misma probabilidad
de selección y por lo tanto la frecuencia esperada de bebidas vendidas en cada uno
de ellos debería ser aproximadamente la misma. Como se han vendido en total 70
refrescos, la frecuencia esperada en cada canal es
Ei = n * pi = 70* ¼ = 17.5 i = 1, ..., k
El estadístico del contraste sería:
Este valor debemos compararlo con el valor crítico de la distribución
con (4-1)=3 grados de libertad.
Este valor es:
Puesto que el valor del estadístico (2.34) es menor que el valor crítico, no podemos
rechazar la hipótesis de que los datos se ajustan a una distribución uniforme. Es
decir, que los canales son seleccionados aleatoriamente entre los consumidores.
9.3 PROBLEMAS
1. si X ~ t (k), ¿Cuál es la distribución de X2?
2. se supone que el peso de unos insectos de determinada especie esta normalmente
distribuido con una desviaron estandar de 0.7 gramos. Si estas suposiciones son
correctas, ¿Cuál es la probabilidad de que una muestra aleatoria de 10 insectos arroje
una varianza mayor o igual a 0.85?
EDUCA INTERACTIVA
Pág. 38
UNIVERSIDAD JOSE CARLOS MARIATEGUI
3. El numero de defectos por unidad observada en una muestra de 100 radios dio la
siguiente distribución de frecuencias
Numero de defectos
Numero de radios
0
28
1
32
2
15
3
10
4
6
5
4
6
3
7
2
Verificar si la distribución de estos datos se aproxima a una distribución Poisson. Use
α = 0.05
Pág. 39
EDUCA INTERACTIVA