1. No category

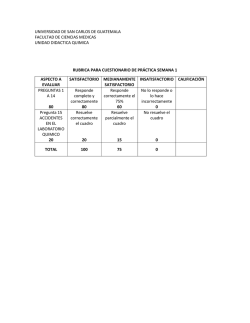
GERENCIA REGIONAL DE EDUCACIÓN
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
COMPETENCIA: Resuelve problemas de cantidad
ESTÁNDAR
• Resuelve problemas referidos a una o más acciones de comparar, igualar, repetir o repartir cantidades,
partir y repartir una cantidad en partes iguales; las traduce a expresiones aditivas, multiplicativas y la
potenciación cuadrada y cúbica; así como a expresiones de adición, sustracción y multiplicación con
fracciones y decimales (hasta el centésimo).
• Expresa su comprensión del sistema de numeración decimal con números naturales hasta seis cifras, de
divisores y múltiplos, y del valor posicional de los números decimales hasta los centésimos; con lenguaje
numérico y representaciones diversas.
• Representa de diversas formas su comprensión de la noción de fracción como operador y como cociente,
así como las equivalencias entre decimales, fracciones o porcentajes usuales.
• Selecciona y emplea estrategias diversas, el cálculo mental o escrito para operar con números naturales,
fracciones, decimales y porcentajes de manera exacta o aproximada; así como para hacer conversiones de
unidades de medida de masa, tiempo y temperatura, y medir de manera exacta o aproximada usando la
unidad pertinente. Justifica sus procesos de resolución así como sus afirmaciones sobre las relaciones
entre las cuatro operaciones y sus propiedades, basándose en ejemplos y sus conocimientos matemáticos.
CAPACIDADES




Traduce cantidades a
expresiones numéricas.
Comunica su
comprensión sobre los
números y las
operaciones.
Usa estrategias y
procedimientos de
estimación y cálculo.
Argumenta
afirmaciones sobre
relaciones numéricas y
las operaciones.
INDICADORES
N°
PREGUNTA
Resuelve problemas referidos a una o más acciones de
comparar, las traduce a expresiones aditivas o multiplicativas
3
Resuelve problemas y selecciona estrategias, para operar con
fracciones usando las unidades pertinentes.
6
Resuelve problemas referidos a una o más acciones de
combinación, para formar una tercera utilizando diversas
representaciones matemáticas.
Resuelve problemas empleando diversas estrategias, para
operar con números naturales y usa diversas
representaciones para mostrar sus conocimientos
matemáticos.
8
4
COMPETENCIA Resuelve problemas de regularidad, equivalencia y cambio.
ESTÁNDAR



Resuelve problemas de equivalencias, regularidades o relaciones de cambio entre dos magnitudes o entre
expresiones; traduciéndolas a ecuaciones que combinan las cuatro operaciones, a expresiones de
desigualdad o a relaciones de proporcionalidad directa, y patrones de repetición que combinan criterios
geométricos y cuya regla de formación se asocia a la posición de sus elementos.
Expresa su comprensión del término general de un patrón, las condiciones de desigualdad expresadas con
los signos > y <, así como de la relación proporcional como un cambio constante; usando lenguaje
matemático y diversas representaciones.
Emplea recursos, estrategias y propiedades de las igualdades para resolver ecuaciones o hallar valores que
cumplen una condición de desigualdad o proporcionalidad; así como procedimientos para crear, continuar o
completar patrones.
Realiza afirmaciones a partir de sus experiencias concretas, sobre patrones

CAPACIDADES

INDICADORES
Traduce cantidades a Resuelve problemas de equivalencias entre dos magnitudes
expresiones numéricas. traduciéndolas a relaciones de proporcionalidad directa y cuya
regla de formación se asocia a la posición de sus elementos.
N°
PREGUNTA
1
GERENCIA REGIONAL DE EDUCACIÓN



Comunica su
comprensión sobre los
números y las
operaciones.
Usa estrategias y
procedimientos de
estimación y cálculo.
Argumenta
afirmaciones sobre
relaciones numéricas y
las operaciones.
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
Resuelve problemas de ecuaciones usando diversas
estrategias
Resuelve problemas aplicando estrategias de cálculo, para
hallar la regla de formación de un patrón.
Resuelve problemas elaborando afirmaciones sobre los
elementos no inmediatos que continúan un patrón. Así
también, justifica sus procesos de resolución.
11
12
14
COMPETENCIA Resuelve problemas de forma, movimiento y localización
ESTÁNDAR
 Resuelve problemas en los que modela características y datos de ubicación de los objetos a formas
bidimensionales y tridimensionales, sus elementos, propiedades, su movimiento y ubicación en el plano
cartesiano.
 Describe estas formas reconociendo ángulos rectos, número de lados y vértices del polígono, así como líneas
paralelas y perpendiculares, identifica formas simétricas y realiza traslaciones, en cuadrículas.
 Así también elabora croquis, donde traza y describe desplazamientos y posiciones, usando puntos cardinales
y puntos de referencia. Usa lenguaje geométrico.
 Emplea estrategias y procedimientos para trasladar y construir formas a través de la composición y
descomposición, y para medir la longitud, superficie y capacidad de los objetos, usando unidades
convencionales y no convencionales, recursos e instrumentos de medición.
 Elabora afirmaciones sobre las figuras compuestas; así como relaciones entre una forma tridimensional y su
desarrollo en el plano; las explica con ejemplos concretos y gráfico
CAPACIDADES




Modela objetos con
formas geométricas
y sus
transformaciones
Comunica su
comprensión sobre
las formas y
relaciones
geométricas
Usa estrategias y
procedimientos
para orientarse en
el espacio
Argumenta
afirmaciones sobre
relaciones
geométricas
INDICADORES
Resuelve problemas, empleando estrategias para medir la
superficie usando recursos e instrumentos de medición.
Resuelve problemas para medir la capacidad de los objeto usando
unidades no convencionales, recursos e instrumentos de medición.
Resuelve problemas aplicando estrategias de cálculo para medir,
de manera exacta, la capacidad (litros) de los objetos.
N°
PREGUNTA
2
5
13
Resuelve problemas de donde traza y describe desplazamientos y
posiciones, usando puntos cardinales y puntos de referencia. Usa
lenguaje geométrico
15
GERENCIA REGIONAL DE EDUCACIÓN
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
COMPETENCIA Resuelve problemas de gestión de datos e incertidumbre.
ESTÁNDAR
 Resuelve problemas relacionados con temas de estudio, en las que reconoce variables cualitativas o
cuantitativas discretas, recolecta datos a través de encuestas y de diversas fuentes de información.
 Selecciona tablas de doble entrada, gráficos de barras dobles y gráficos de líneas, seleccionando el más
adecuado para representar los datos.
 Usa el significado de la moda para interpretar información contenida en gráficos y en diversas fuentes de
información.
 Realiza experimentos aleatorios, reconoce sus posibles resultados y expresa la probabilidad de un evento
relacionando el número de casos favorables y el total de casos posibles.
 Elabora y justifica predicciones, decisiones y conclusiones, basándose en la información obtenida en el
análisis de datos o en la probabilidad de un evento
CAPACIDADES




Representa
datos
con
gráficos
y
medidas
estadísticas o probabilísticas
Comunica la comprensión de
los conceptos estadísticos y
probabilísticos
Usa
estrategias
y
procedimientos
para
recopilar y procesar datos
Sustenta conclusiones o
decisiones
en
base
a
información obtenida
INDICADORES
Resuelve problemas relacionados con recolección de
datos.
Resuelve problemas de ocurrencia de sucesos usando
nociones de “más probables” o “menos probables”.
Resuelve problemas de experimentos aleatorios,
expresando la probabilidad de un evento relacionando
el número de casos favorables y el total de casos
posibles
N°
PREGUNTA
9
10
7
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
GERENCIA REGIONAL DE EDUCACIÓN
ORIENTACIONES PARA LA CALIFICACIÓN DE LA PRUEBA DE MATEMÁTICA DEL QUINTO GRADO DE
PRIMARIA
Estimado docente:
En esta oportunidad le estamos presentando una prueba con preguntas abiertas con la
finalidad de garantizar la compresión con el uso de estrategias como por ejemplo al
subrayado, el parafraseo y otros que ud. vienen aplicando.
Se sugiere que el estudiante desarrolle el proceso de resolución en la misma prueba papa
identificar con precisión aciertos y dificultades.
La prueba de matemática para el quinto grado, consta de 10 preguntas. La duración de la
prueba es aproximadamente 60 minutos.
El docente aplicador debe propiciar en lo posible un clima emocional de confianza apropiado y
estimulante para el estudiante.
En correspondencia a la naturaleza de la prueba el docente aplicador deberá de leer las
preguntas en caso de ser necesario; para facilitar el desarrollo de la prueba.
Las respuestas son los siguientes:
En las dos primeras preguntas se debe poner en evidencia la comprensión lectora que ayudara
mucho en la resolución de las preguntas.
1. Respuesta correcta la c.
2. Respuesta correcta es 2304 cm2
3. Respuesta: b
4. Respuesta: S/.30
5. Respuesta correcta b.
6. Respuesta: c
7. Respuesta: c
8. Respuesta: b
9. Repuesta b
10. Respuesta b
11 Respuesta: S/. 9 tercer hijo; S/. 19 segundo hijo y S/. 29 primer hijo
12-Respuesta 1; 4; 7: 10: 13: 16.
13. Respuesta: 4,3 l. ó 43 dl.
14. Respuesta La respuesta sería la alternativa a. Beto
15. Repuesta:
Se debera tener en cuenta la formación simbólica de un par ordenado (x;y) y la regla de reducción
(x; y)
r
(x – 3 ; y – 1)
(x; y)
r
E(6;2)
F(10;2)
G(10;8)
H (6;8)
(x ÷ 2 ; y ÷ 2)
E (3; 1)
F(5; 1)
G(5;4)
H (3; 4)
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
GERENCIA REGIONAL DE EDUCACIÓN
PRUEBA SALIDA
EMCEREP 2016
MATEMÁTICA
QUINTO GRADO
APELLIDOS:
NOMBRES:
INSTITUCIÓN EDUCATIVA:
SECCIÓN:
FECHA:
GERENCIA REGIONAL DE EDUCACIÓN
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
Lee con atención la siguiente situación.
Pasadizo de mayólicas:
Vicente, desea remodelar su pasadizo para las fiestas de fin de año, contrata un albañil para que
coloque mayólicas negras, blancas y grises para cubrir el pasadizo de su casa siguiendo una secuencia.
Observa:
Utiliza esta información para resolver las preguntas 1, 2 y 3:
1.- Para saber la cantidad de mayólicas blancas y negras que se utilizarán, el albañil elabora la
siguiente tabla:
Si coloca 24 mayólicas blancas, ¿cuántas mayólicas negras utilizará?
a. 96 mayólicas negras
b. 78 mayólicas negras
c. 73 mayólicas negras
d. 16 mayólicas negras
2. Se quiere saber la superficie que se cubre con las mayólicas blancas, grises y negras que se
muestran a continuación:
La mayólica blanca y las grises son cuadradas. El lado de la mayólica blanca mide 24 cm y el lado de la
mayólica gris es la mitad que el de la mayólica blanca. ¿Cuánto mide la superficie total cubierta por
todas las mayólicas mostradas en la figura 1?
Respuesta: la superficie total mide ………………………………… cm 2
GERENCIA REGIONAL DE EDUCACIÓN
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
3. Como se rompieron 12 mayólicas blancas, el albañil tuvo que ir a la tienda a comprarlas. En la
tienda solo se venden mayólicas blancas en cajas de 5 unidades, al precio que se indica:
¿Cuánto dinero se gastará en esta compra?
a. S/ 342,00
b. S/ 85,50
c. S/ 57,00
d. S/ 28,50
4. Por fiestas de fin de año en un mercado se ofrece la siguiente oferta:
Ana necesita comprar 20 bolsas para venderlas en su tienda. Usando la oferta,
¿Cuánto pagará por las 20 bolsas de avena?
GERENCIA REGIONAL DE EDUCACIÓN
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
5. Se desea llenar la caja mostrada con libros del mismo tamaño. Si se colocan tal como se muestra en
la figura, entran 3 libros a lo largo y 2 libros a lo ancho. ¿Cuántos libros como máximo pueden entrar
en esta caja?
a. 50 libros.
b. 30 libros.
c. 10 libros.
d. 6 libros.
6. Carlos y Reyna tienen que barrer el patio de la escuela luego de la celebración del dia de logro.
Carlos barrió 2/5 del patio y Reyna 3/8. ¿Qué fracción del patio quedara sin barrer?
a. 1/40
b. 6/40
c. 9/ 40
d. 31/40
7. La caja mostrada tiene bolas blancas y negras. ¿Cuál es la probabilidad de extraer, al azar, una bola
blanca en el primer intento?
a.
b.
c.
d.
1/3
3/4
3/7
1/7
8. Se necesita formar una pareja de baile conformada por un hombre y una mujer. Esta pareja se
escogerá al azar. Para ello, se colocan los nombres de los candidatos en dos bolsas, una para los
hombres y la otra para mujeres. Observa:
¿Cuántas opciones existen para elegir la pareja de baile?
a.15
b. 9
c. 6
d. 2
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
GERENCIA REGIONAL DE EDUCACIÓN
9. Luego de realizar un paseo al zoológico de la ciudad, los estudiantes del quinto grado con la
recolección de datos realizaron el siguiente grafico de barras
Escribe V (verdadero) o F (Falso), según corresponda. Luego, encierra con una la alternativa correcta:
a. Hay más boas que caimanes.
b. Hay menos cobras que tortugas.
c. Hay igual cantidad de caimanes
y cobras que de tortugas.
d. Hay 3 boas más que caimanes.
(
(
)
)
(
(
)
)
a. V V V F
c. V F F V
b. V V F V
d. V V V F
10. Un dado se lanza 2 veces consecutivas
I ¿Cuál es la probabilidad de obtener un número impar en el primer lanzamiento?
a. 1/6
b. 1/2
c. 1/3
d. 1/12
e. 5/36
11. Resuelve la siguiente situación problemática utilizando ecuaciones:
Una madre reparte S/. 57 entre tres hijos de forma que el mayor recibe S/. 10 más que el segundo, y
este S/. 10 más que el tercero ¿Cuánto recibe cada uno?
12. El cuarto término de una progresión aritmética es 10, y el sexto es 16. Escribir la progresión
……………………………………………………………………………………………………………………………………………………..
GERENCIA REGIONAL DE EDUCACIÓN
SISTEMA DE EVALUACIÓN DE LOS APRENDIZAJES – 2016
13. Pedro ha comprado un juego completo de cacerolas para cuando se mude a su casa nueva. La
cacerola más pequeña tiene una capacidad de 15 decilitros, que es una capacidad 2,8 litros menor que
la de la cacerola más grande del juego. ¿Qué capacidad tiene la cacerola más grande en litros?
14. Andrés, Beto y Carlín se encuentran charlando sentados alrededor de una mesa circular. Beto no
está a la derecha de Carlín. ¿Quién está a la derecha de Andrés?
A) Beto
B) Carlín
C) No se sabe.
D) Ay B
E) N.A
15.- Completa la siguiente tabla y luego reduce el polígono, siguiendo la regla de reducción:
(x; y)
r
E(6;2)
F(10;2)
G(10;8)
H (6;8)
(x – 3 ; y – 1)
E (3;1)