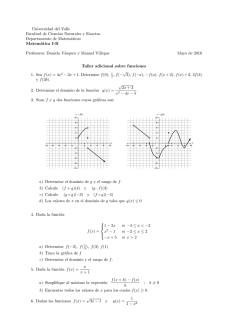
z - Universidad de Granada
VARIABLE COMPLEJA L. L. Salcedo Departamento de Fı́sica Atómica, Molecular y Nuclear, Universidad de Granada, E-18071 Granada, Spain E-mail: [email protected] 3 de octubre de 2016 Resumen Apuntes completos de la asignatura de métodos matemáticos. Incluye transformadas integrales y series de Fourier. Versión v5.29. 2006-2016. Se ruega comunicar los errores que puedan encontrarse a [email protected]. http://www.ugr.es/local/salcedo/public/mmf3/curso.pdf Índice 1. Números complejos 9 1.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.2. El cuerpo de los números complejos . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.2.1. Definición de suma y producto . . . . . . . . . . . . . . . . . . . . . . . . 10 1.2.2. Propiedades de suma y producto . . . . . . . . . . . . . . . . . . . . . . . 10 1 1.2.3. C como extensión de R . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.2.4. Unidad imaginaria. Notación binómica . . . . . . . . . . . . . . . . . . . . 11 1.2.5. Parte real, parte imaginaria, complejo conjugado . . . . . . . . . . . . . . . 12 1.3. Representaciones. El plano complejo. . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.1. El plano complejo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.3.2. Módulo de un número complejo . . . . . . . . . . . . . . . . . . . . . . . . 14 1.3.3. Representación polar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.3.4. Argumento. Determinación principal. . . . . . . . . . . . . . . . . . . . . . 15 1.3.5. Producto, división y conjugado en representación polar . . . . . . . . . . . . 16 1.3.6. Potencias enteras de un número complejo . . . . . . . . . . . . . . . . . . . 17 1.4. Teorema de Moivre. Fórmula de Euler. . . . . . . . . . . . . . . . . . . . . . . . . 17 1.4.1. Teorema de Moivre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 1.4.2. Fórmula de Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 1.5. Raı́ces de un número complejo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2. Lı́mites en el plano complejo 20 2.1. El principio de los intervalos encajados . . . . . . . . . . . . . . . . . . . . . . . . 20 2.2. Puntos lı́mite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 2.3. Sucesiones complejas convergentes . . . . . . . . . . . . . . . . . . . . . . . . . . 21 2.4. Esfera de Riemann y plano complejo extendido . . . . . . . . . . . . . . . . . . . . 23 3. Funciones complejas 25 2 3.1. Variables y funciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 3.2. Curvas y dominios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 3.3. Continuidad de funciones complejas . . . . . . . . . . . . . . . . . . . . . . . . . . 28 3.4. Continuidad uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 4. Derivación en el plano complejo 32 4.1. Derivada de una función compleja . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 4.2. Las ecuaciones de Cauchy-Riemann . . . . . . . . . . . . . . . . . . . . . . . . . . 34 4.3. Complementos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 5. Integración en el plano complejo 40 5.1. La integral de una función compleja . . . . . . . . . . . . . . . . . . . . . . . . . . 40 5.2. Propiedades básicas de la integral . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 5.3. Teorema de la integral de Cauchy . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 5.4. Integrales complejas indefinidas . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 5.5. Fórmula integral de Cauchy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 5.6. Derivabilidad infinita de funciones analı́ticas . . . . . . . . . . . . . . . . . . . . . . 51 5.7. Índice de un camino cerrado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 5.8. Complementos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 6. Series complejas 55 6.1. Convergencia y divergencia de series . . . . . . . . . . . . . . . . . . . . . . . . . . 55 3 6.2. Convergencia absoluta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 6.3. Convergencia uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 7. Series de potencias 61 7.1. Teorı́a básica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 7.2. Determinación del radio de convergencia . . . . . . . . . . . . . . . . . . . . . . . 63 8. Exponencial y funciones relacionadas 66 8.1. Exponencial, coseno y seno . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66 8.2. Funciones hiperbólicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 8.3. Derivadas de exp, cos, sen, cosh, senh . . . . . . . . . . . . . . . . . . . . . . . . 69 8.4. Función logaritmo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70 8.5. Función potencia general . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 8.6. Funciones trigonométricas inversas . . . . . . . . . . . . . . . . . . . . . . . . . . 74 9. Funciones multivaluadas 75 9.1. Dominios de univalencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75 9.1.1. Potencia y raı́z n-ésima . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 9.1.2. Exponencial y logaritmo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 9.2. Ramas y puntos de ramificación . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 9.3. Superficies de Riemann . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 9.4. Integración y funciones multivaluadas . . . . . . . . . . . . . . . . . . . . . . . . . 88 4 10.Series de Taylor 93 10.1. Desarrollo de una función analı́tica . . . . . . . . . . . . . . . . . . . . . . . . . . 93 10.1.1. Sobre el cálculo de series de Taylor . . . . . . . . . . . . . . . . . . . . . . 95 10.2. Puntos regulares y singulares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 10.3. Teoremas de unicidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98 10.4. Ceros de una función analı́tica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 10.5. Principio del módulo máximo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101 11.Series de Laurent 103 11.1. Desarrollo de Laurent de una función analı́tica . . . . . . . . . . . . . . . . . . . . 103 11.1.1. Series de potencias negativas . . . . . . . . . . . . . . . . . . . . . . . . . 103 11.2. Puntos singulares aislados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 11.3. Del cálculo de series de Laurent: . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112 11.4. Residuos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 11.4.1. Cálculo de residuos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114 11.4.2. Residuo en el punto del infinito . . . . . . . . . . . . . . . . . . . . . . . . 115 11.4.3. Cálculo del residuo en el infinito . . . . . . . . . . . . . . . . . . . . . . . . 116 12.Aplicación del teorema de los residuos y otros resultados generales 118 12.1. Evaluación de integrales impropias . . . . . . . . . . . . . . . . . . . . . . . . . . . 118 12.1.1. Valor principal de Cauchy . . . . . . . . . . . . . . . . . . . . . . . . . . . 121 12.1.2. Integrales impropias en C . . . . . . . . . . . . . . . . . . . . . . . . . . . 122 5 12.1.3. Lemas de integración . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122 12.1.4. Integrales impropias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124 12.2. Suma de series . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140 12.3. Residuo logarı́tmico y principio de variación del argumento . . . . . . . . . . . . . . 141 12.4. Teorema de Rouché . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 12.5. Prolongación analı́tica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 12.5.1. Principio de reflexión de Schwarz . . . . . . . . . . . . . . . . . . . . . . . 147 13.Transformada de Laplace 148 13.1. Transformada de Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148 13.2. Reglas operativas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149 13.3. Transformada inversa de Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . 151 13.4. Reglas operativas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151 13.5. Fórmula de inversión de Bronwich . . . . . . . . . . . . . . . . . . . . . . . . . . . 152 14.Series de Fourier 155 14.1. Forma compleja de la serie de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . 155 14.2. Forma trigonométrica de la serie de Fourier . . . . . . . . . . . . . . . . . . . . . . 158 14.3. Series de Fourier seno y coseno . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159 14.4. Complementos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161 15.Transformada de Fourier 162 6 15.1. Transformada de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162 15.2. Transformada inversa de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162 15.3. Propiedades de la transformada de Fourier . . . . . . . . . . . . . . . . . . . . . . 163 15.4. Ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165 15.5. Transformada de Fourier multidimensional . . . . . . . . . . . . . . . . . . . . . . 167 15.6. Función escalón . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167 15.6.1. Regularizaciones de H(x) . . . . . . . . . . . . . . . . . . . . . . . . . . . 167 15.6.2. Transformada de Laplace de la función de escalón . . . . . . . . . . . . . . 168 15.6.3. Transformada de Fourier de la función de escalón . . . . . . . . . . . . . . . 168 15.7. Función δ de Dirac . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169 15.7.1. Propiedad básica de δ(t) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169 15.7.2. Otras propiedades de δ(t) . . . . . . . . . . . . . . . . . . . . . . . . . . . 170 15.7.3. Regularizaciones de δ(t) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 15.7.4. Transformada de Laplace de δ(t) . . . . . . . . . . . . . . . . . . . . . . . 173 15.7.5. Transformada de Fourier de δ(t) . . . . . . . . . . . . . . . . . . . . . . . . 173 15.8. Complementos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173 15.8.1. Transformada inversa de Fourier . . . . . . . . . . . . . . . . . . . . . . . . 173 15.8.2. Identidad de Weierstrass . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174 16.Bibliografı́a 175 A. Integrales y series 176 7 B. Transformada de Laplace 178 C. Ejercicios 179 8 Números complejos 1. 1.1. Introducción Se suponen conocidas las definiciones y propiedades de los números reales R. Los números reales no son algebraicamente cerrados, es decir, pueden escribirse ecuaciones que involucran sólo reales que no admiten solución dentro R. Por ejemplo: 1 2 x −x+5=0 2 con solución formal x=1± √ √ −9 = 1 ± 3 −1 . (1.1) (1.2) No tiene solución para x ∈ R real. Tendrı́a solución en una extensión de los reales en la que −1 tuviera raı́z cuadrada. Tal raı́z se suele denominar i i2 = −1 . (1.3) Si x ∈ R necesariamente x2 ≥ 0, luego i no es real. i se denomina unidad imaginaria. En este caso las soluciones serı́an 1 ± 3i. Si se admite esta extensión, tendremos números “complejos” del tipo z = x + iy , x, y ∈ R . (1.4) Usando la propiedad i2 = −1 se puede ver que los números complejos ası́ construidos son cerrados bajo suma y multiplicación, si se aplican las propiedades usuales válidas para reales: (x1 + iy1 ) + (x2 + iy2 ) = (x1 + x2 ) + i(y1 + y2 ) (x1 + iy1 )(x2 + iy2 ) = x1 x2 + ix1 y2 + iy1 x2 + i2 y1 y2 = (x1 x2 − y1 y2 ) + i(x1 y2 + y1 x2 ) . (1.5) (1.6) El problema de postular propiedades es que no está garantizado que no se llegue a inconsistencias.1 Para evitar este problema es mejor proceder constructivamente. 1 Paradojas: r r √ √ √ √ 1 1 1 1 = √ implica − 1 = −1 −1 = −1 = −1 √ = +1 . a −1 a −1 √ En realidad hay dos raı́ces cuadradas, ± a. Cuando a > 0 las dos raı́ces se distinguen bien porque√una es positiva √ y la otra es negativa pero eso deja de ser cierto cuando a < 0 y la falacia es que se ha identificado + −1 con − −1. Lo único que se concluye es ±1 = ±1. 9 Los números complejos también iluminan problemas puramente reales. Por ejemplo, la función 1 es perfectamente regular para todo x real, sin embargo si se considera su desarrollo f (x) = 1 + x2 en serie de Taylor en torno a x = 0, se encuentra la serie geométrica 1 − x2 + x4 − x6 + · · · que converge sólo si |x| < 1. En R no se ve el motivo de la falta de convergencia para x > 1 ó x < −1, dado que nada especial le ocurre a la función en x = ±1. Como se verá el motivo es obvio cuando se considera la extensión de esta función al plano complejo. El cuerpo de los números complejos 1.2. 1.2.1. Definición de suma y producto Matemáticamente se introduce el conjunto de números complejos C = (R × R, +, .) como el conjunto de pares ordenados de números reales, R × R, z = (x, y) ∈ C, dotado de las siguientes propiedades2 (x1 , y1 ) = (x2 , y2 ) sii x1 = x2 , y1 = y2 (x1 , y1 ) + (x2 , y2 ) := (x1 + x2 , y1 + y2 ) (x1 , y1 )(x2 , y2 ) := (x1 x2 − y1 y2 , x1 y2 + y1 x2 ) 1.2.2. (igualdad), (suma), (multiplicación). (1.7) (1.8) (1.9) Propiedades de suma y producto De las definiciones se deduce que C es un cuerpo (es decir, aritméticamente los complejos se comportan igual que los reales): a) La suma define un grupo abeliano. El neutro de la suma es (0, 0) se representa por 0 (cero) . El inverso respecto de la suma (opuesto) de z se representa por −z z = (x, y), −z = (−x, −y), z + (−z) = 0 . (1.10) z1 , z2 ∈ C . (1.11) Se define la resta en C z1 − z2 := z1 + (−z2 ), 2 Usamos la notación a := b para indicar que a está definido como b. 10 b) El producto define un grupo abeliano en C − {0}. Satisface la propiedades conmutativa y asociativa. El neutro del producto es (1, 0), se denomina 1 (uno). Todo z 6= 0 tiene un inverso que se denota z −1 (o también 1/z) z = (x, y), z −1 = (x′ , y ′ ), zz −1 = 1 y x xx′ − yy ′ = 1 −1 , ,− z = xy ′ + yx′ = 0 x2 + y 2 x2 + y 2 z 6= 0 (1.12) Se define la división de complejos z1 := z1 z2−1 , z2 z1 , z2 ∈ C , z2 6= 0 . (1.13) c) Propiedad distributiva: z1 (z2 + z3 ) = z1 z2 + z1 z3 . 1.2.3. C como extensión de R Se comprueba inmediatamente que el subconjunto {(x, 0), x ∈ R} ⊂ C es un cuerpo isomorfo a R. A partir de ahora identificamos x con (x, 0) x = (x, 0), x∈R (1.14) de modo que R ⊂ C y los complejos son una extensión de los reales. 1.2.4. Unidad imaginaria. Notación binómica Por otro lado si se define la unidad imaginaria i i := (0, 1), i2 = (0, 1)(0, 1) = (−1, 0) = −1 , (1.15) cualquier número complejo z = (x, y) puede escribirse en la llamada forma binómica, z = x + iy , z ∈ C, x, y ∈ R . (1.16) En efecto: x + iy = (x, 0) + (0, 1)(y, 0) = (x, 0) + (0, y) = (x, y) . (1.17) Como se ve de la construcción, los números reales x e y tales que z = x + iy, son únicos. La forma binómica es la más frecuentemente utilizada. 11 Nota: Para evitar falacias (ej. nota 1, al pie de página) es importante notar que i no se define como la raı́z cuadrada de −1. De hecho es una de las dos raı́ces cuadradas de −1. La otra raı́z es −i = (0, −1). Nótese también que i−1 = −i. En efecto: i(−i) = −i2 = −(−1) = 1. 1.2.5. Parte real, parte imaginaria, complejo conjugado Para z = (x, y), se define x = Re (z) y = Im (z) z ∗ = (x, −y) parte real de z, parte imaginaria de z, complejo conjugado de z. (A veces se denota z.) (1.18) Nota: Obsérvese que, por definición, la “parte imaginaria” de z es un número real; no incluye la i.3 La aplicación z 7→ z ∗ es un automorfismo en C (conserva suma y producto):4 (z1 + z2 )∗ = z1∗ + z2∗ , (z1 − z2 )∗ = z1∗ − z2∗ , (z1 z2 )∗ = z1∗ z2∗ , (z1 /z2 )∗ = z1∗ /z2∗ , (1.19) y una conjugación, (z ∗ )∗ = z . Se deduce Re (z) = z + z∗ , 2 Im (z) = (1.20) z − z∗ , 2i (1.21) y por tanto, z ∈ R sii Im (z) = 0 o equivalentemente z ∗ = z , z ∈ iR sii Re (z) = 0 o equivalentemente z ∗ = −z . (1.22) (1.23) Los números de la forma iR se denominan imaginarios puros. El producto zz ∗ = x2 + y 2 ≥ 0 (1.24) 3 Estrictamente Im (z) es la componente de z en la dirección imaginaria, pero se denomina parte imaginaria para abreviar. 4 Puesto que la definición básica es i2 = −1 y ésta no distingue i de −i tan natural es z como z ∗ : si en una ecuación se cambian todas las i por −i la ecuación seguirá siendo cierta. 12 y= Im z 2i z=2+i i 1 0 1 2 x=Re z z* =2 i i Figura 1: Plano complejo. es real (y no negativo). Esto permite calcular fácilmente el inverso de un número complejo: z −1 = (x + iy)−1 = z∗ x − iy x −y 1 = ∗ = 2 = 2 +i 2 2 2 z zz x +y x +y x + y2 (z 6= 0) . (1.25) Observación: La definición de suma y producto en C es tal que todas las ecuaciones de 2 grado con coeficientes reales tienen solución en C. También las ecuaciones con coeficientes complejos tienen solución. Es más todas las ecuaciones polinómicas complejas de cualquier grado tienen solución en C (teorema fundamental del álgebra). C es algebraicamente cerrado y no son necesarias nuevas extensiones. De hecho no existen otros cuerpos basados en Rn , n ≥ 2. ◦ 1.3. 1.3.1. Representaciones. El plano complejo. El plano complejo Ya hemos visto dos formas de representar los número complejos, (x, y) y forma binómica x + iy. C tiene estructura de espacio vectorial sobre R de dimensión 2 y es geométricamente equivalente al plano R2 : (x, y) representan las dos componentes cartesianas del punto z en el plano euclı́deo R2 en la base ortonormal formada por {1, i}. La suma de números complejos es equivalente a su suma como vectores de R2 . z = (x, y) se puede representar por el punto (x, y) del plano complejo (o plano de Argand), o equivalentemente por el vector que va de (0, 0) a (x, y). El eje x se denomina eje real y el eje 13 y eje imaginario.5 Nótese que z ∗ es el vector reflejado de z respecto del eje real. (Véase la fig. 1.) Las regiones {y > 0}, e {y < 0} se denominan semiplano superior y semiplano inferior, respectivamente. Las regiones {x > 0, y > 0}, {x < 0, y > 0}, {x < 0, y < 0} y {x > 0, y < 0} se denominan primer, segundo, tercer y cuarto cuadrante, respectivamente. La equivalencia geométrica entre C y R2 implica en particular que en C, a diferencia de R, no existe un orden natural entre números complejos.6 Notación: cuando se use a > b, a ≤ b, etc, automáticamente se sobreentiende que a, b son reales. 1.3.2. Módulo de un número complejo El módulo del número complejo z = (x, y) se define como la norma euclı́dea (longitud) del vector correspondiente: p √ |z| := + x2 + y 2 = + zz ∗ ≥ 0 (1.26) Es definido no negativo y para z real coincide con el valor absoluto. El módulo cumple |z| |z1 z2 | |z ± z2 |2 1 |z1 | − |z2 | = = = ≤ 0 , sii z = 0 , |z1 ||z2 | , |z1 /z2 | = |z1 |/|z2 | , 2 2 |z1 | + |z2 | ± 2 Re (z1 z2∗ ) , |z1 + z2 | ≤ |z1 | + |z2 | (Desigualdad triangular) . (1.27) Considerados como vectores en R2 ~z1 · ~z2 = Re (z1 z2∗ ) (con el producto escalar euclı́deo usual). 1.3.3. Representación polar Los números complejos se pueden representar mediante coordenadas polares r y θ. r es el módulo de z y θ el ángulo que forma el vector z con el semieje real positivo. El ángulo se toma en 14 y=r sen θ r z=x+iy θ x= r cos θ Figura 2: Coordenadas polares. sentido positivo que por definición es el antihorario. (Véase la fig. 2.) z = x + iy , r = |z| , x = r cos θ y = r sen θ tan θ = y/x . z = r(cos θ + i sen θ) (1.28) Nótese que la última ecuación no distingue entre z y −z, es decir, entre θ y θ + π. Hace falta conocer por ejemplo el cuadrante en el que está z. 1.3.4. Argumento. Determinación principal. El ángulo θ se denomina argumento de z y se designa arg z. El argumento sólo está definido salvo un múltiplo entero de 2π ya que cos θ y sen θ son funciones periódicas. Por ejemplo, θ = 3π/2 y θ = −π/2 son ambos argumentos de z = −i. En general si θ es un argumento de z, todos los valores θ + 2πn = arg z , n∈Z (z 6= 0) (1.29) son también argumentos de z. arg z es una función multivaluada de z. Para evitar ambigüedades se puede elegir una determinación principal del argumento, que se designa Arg z. Nosotros 5 Históricamente, el plano complejo, introducido por Gauss y Argand, contribuyó a la aceptación de los números complejos, ya que probaba que éstos “existı́an”. 6 Como conjunto, es posible definir un orden total en C (de hecho de muchas formas) pero no uno que sea compatible con la estructura algebraica como en R. Por ejemplo, en R, si a 6= 0, necesariamente a > 0 ó −a > 0 (una y una sola de las dos posibilidades), y si a > 0 y b > 0, entonces ab > 0. En C no se puede definir un orden “>” con estas propiedades. 15 tomaremos Arg z ∈ [0, 2π[ , arg z = Arg z + 2πn , n ∈ Z. (1.30) Nótese que esta elección de la determinación principal es arbitraria y no es universal. También se encuentra con frecuencia la elección Arg z ∈ ] − π, π].7 Ninguna elección produce una función continua. La función arg no está definida para z = 0. Algunos casos particulares son: Arg (1) = 0, 1.3.5. Arg (i) = π/2, Arg ( − i) = 3π/2, Arg ( − 1) = π . (1.31) Producto, división y conjugado en representación polar La representación polar es particularmente práctica para representar la multiplicación y división de complejos: z1 = r1 (cos θ1 + i sen θ1 ) , z2 = r2 (cos θ2 + i sen θ2 ) , z1 z2 = r1 r2 (cos θ1 cos θ2 − sen θ1 sen θ2 + i cos θ1 sen θ2 + i sen θ1 cos θ2 ) = r1 r2 (cos(θ1 + θ2 ) + i sen(θ1 + θ2 )) , (1.32) Es decir,8 |z1 z2 | = |z1 ||z2 | , arg(z1 z2 ) = arg(z1 ) + arg(z2 ) + 2πn , n ∈ Z, z1 , z2 6= 0 . (1.33) Más generalmente, por inducción,9 |z1 · · · zn | = |z1 | · · · |zn | , arg(z1 · · · zn ) = arg(z1 ) + · · · + arg(zn ) (1.34) ( mód 2π) . Igualmente 7 z1 = |z1 | , arg z1 = arg(z1 ) − arg(z2 ) ( mód 2π) , z2 |z2 | z2 −1 −1 |z | = |z| , arg(z −1 ) = − arg(z) ( mód 2π) , (1.35) Más generalmente, Argα z = Arg (e−iα z) + α produce el argumento enel intervalo [α, α + 2π[. 0, 0 ≤ Arg z 1 + Arg z 2 < 2π 8 . Arg (z1 z2 ) = Arg (z1 ) + Arg (z2 ) + 2πn(z1 , z2 ) , donde n(z1 , z2 ) = −1 , 2π ≤ Arg z 1 + Arg z 2 < 4π 9 La notación a = b ( mód c), donde a, b, c son elementos de un grupo abeliano, indica que a − b = nc para algún n ∈ Z. 16 y también |z ∗ | = |z| , arg(z ∗ ) = − arg z ( mód 2π) . (1.36) Ejemplo. El número iz corresponde al vector z rotado 90o en sentido positivo. Potencias enteras de un número complejo 1.3.6. Para n ∈ Z y z ∈ C se define z n en la forma natural: (n factores) n > 0, z · · · z n n = 0, z = 1 −1 −1 z ···z (−n factores) n < 0 , (1.37) (z 6= 0) . Esta definición cumple las propiedades z n z m = z n+m , (z n )m = z nm , n, m ∈ Z . (1.38) (Teorema de Moivre) , (1.39) Teorema de Moivre. Fórmula de Euler. 1.4. Teorema de Moivre 1.4.1. Aplicando la fórmula de suma de argumentos se deduce (cos θ + i sen θ)n = cos(nθ) + i sen(nθ) (n ∈ Z) es decir, cos(nθ) = Re ((cos θ + i sen θ)n ) , sen(nθ) = Im ((cos θ + i sen θ)n ) . (1.40) Por ejemplo, usando (cos θ + i sen θ)2 = cos2 θ − sen2 θ + 2i cos θ sen θ (1.41) se obtienen la conocidas relaciones trigonométricas cos(2θ) = cos2 θ − sen2 θ , sen(2θ) = 2 cos θ sen θ . 17 (1.42) 1.4.2. Fórmula de Euler Es conveniente usar la relación eiθ := cos θ + i sen θ (Fórmula de Euler), (1.43) de modo que un número complejo cualquiera se puede escribir z = reiθ , r ≥ 0, θ ∈ R. (1.44) Cuando se defina la función exponencial compleja se demostrará este resultado. De momento lo tomamos como una notación que puede justificarse10 mediante desarrollo en serie (formal por ahora): ∞ X (−1)n 2n+1 θ +i θ cos θ + i sen θ = (2n)! (2n + 1)! n=0 n=0 X ∞ ∞ X (iθ)2n+1 (iθ)2n (iθ)n = + = = eiθ . (2n)! (2n + 1)! n! n=0 n=0 ∞ X (−1)n 2n (1.45) Con esta notación se puede escribir r1 eiθ1 r1 = ei(θ1 −θ2 ) iθ 2 r2 e r2 r1 eiθ1 r2 eiθ2 = r1 r2 ei(θ1 +θ2 ) , (r2 6= 0) , (1.46) (reiθ )∗ = re−iθ . (1.47) consistente con el comportamiento de la exponencial real. Igualmente 1 (reiθ )−1 = e−iθ , r (reiθ )n = rn einθ (n ∈ Z) , Algunas fórmulas notables: e2πi = 1 , 1.5. eiπ = −1 , i = eiπ/2 , −i = e−iπ/2 . (1.48) Raı́ces de un número complejo Queremos ahora definir z 1/n para√n ∈ Z. En R, x > 0 tiene dos raı́ces cuadradas; la ecuación y 2 = x tiene dos soluciones, y = ± x. En C la ecuación w2 = z también tiene dos soluciones si 10 También se ve que las ecuaciones f (0) = 1 y f ′ (θ) = if (θ) se satisfacen cuando f (θ) = eiθ y cuando f (θ) = cos θ + i sen θ. 18 z 6= 0, ya que si w es una solución, −w también lo es. Sin embargo, a diferencia del caso real, un número complejo no nulo tiene tres raı́ces cúbicas, cuatro raı́ces cuárticas, etc. Se define z 1/n , n ∈ Z, como toda solución de la ecuación wn = z. Si z 6= 0 y n 6= 0 hay exactamente |n| raı́ces distintas. Basta estudiar el caso n positivo: Si n = −m < 0, equivale a 1 resolver wm = . Suponemos n > 0. Sea z z = reiθ , w = ρeiφ , entonces reiθ = ρn einφ , (1.49) que implica11 ρ = r1/n , k ∈ Z. nφ = θ + 2πk , (1.50) La solución es múltiple θ + 2πk , k ∈ Z, n pero no todos los argumentos φk producen wk = ρeiφk distintos. Notando que φ = φk = φk+1 = φk + 2π , n φk+n = φk + 2π , (1.51) (1.52) se ve que sólo hay n soluciones distintas correspondientes a wk con k = 0, 1, . . . , n − 1. Además, si θ ∈ [0, 2π[, φk ∈ [0, 2π[ para k = 0, 1, . . . , n − 1. wk = r1/n ei(θ+2πk)/n = w0 uk , uk = e2πik/n (1.53) donde uk son las raı́ces n-enésimas de la unidad. Las n raı́ces wk están dispuestas en los vértices de un polı́gono regular centrado en 0, y por simetrı́a n−1 X k=0 wk = 0 si n ≥ 2 . 11 (1.54) Se sobreentiende r1/n en el sentido de números reales. Como número complejo r tiene raı́ces complejas, una de las cuales es real y positiva. 19 eiθ 2πi 3 i θ 3 e e eiθ 3 e 4πi 3e i θ 3 Figura 3: Raı́ces cúbicas de eiθ . Lı́mites en el plano complejo 2. 2.1. El principio de los intervalos encajados Teorema. (Principio de los intervalos encajados.) Sea I1 , I2 , . . . una sucesión12 de intervalos cerrados de R, In = [an , bn ], tales que: 1) Están encajados: In+1 ⊂ In . 2) Su longitud (bn − an ) tiende a 0 cuando n → ∞ . Entonces hay un punto, y sólo uno, que pertenece a todos ellos. ♦ Este teorema se generaliza fácilmente al caso complejo: Teorema. (Principio de los rectángulos encajados.) Sea R1 , R2 , . . ., una sucesión de rectángulos cerrados paralelos a los ejes real e imaginario: Rn = [an , bn ] × [cn , dn ] ⊂ C tales que: 1) Están encajados: Rn+1 ⊂ Rn . 2) Su perı́metro tiende a 0 cuando n → ∞ . Entonces hay exactamente un z ∈ C común a todos los rectángulos. ♦ 12 Por sucesión siempre entenderemos sucesión infinita. 20 2.2. Puntos lı́mite Definición. Una sucesión compleja es una aplicación de N en C, n 7→ zn . A menudo la denotaremos {zn }. Definición. Un número complejo α es un punto lı́mite o punto de acumulación de la sucesión compleja z1 , z2 , . . . , zn , . . . , (2.1) si ∀ǫ > 0, la desigualdad |zn − α| < ǫ es válida para infinitos valores de n. Definición. Un entorno (complejo) del punto α de radio ǫ es el disco abierto D(α, ǫ) = {z |z − α| < ǫ}, α ∈ C, ǫ > 0 . (2.2) Análogamente se define entorno reducido como {z 0 < |z − α| < ǫ}, es decir, el entorno excluyendo el propio punto α. Por tanto α es un punto lı́mite de la sucesión {zn } sii en cualquier entorno de α hay infinitos términos de la sucesión. Ejemplo. La sucesión 1, 0, 3, 0, 5, 0, 7, 0, . . . tiene 0 como punto lı́mite. Ejemplo. La sucesión 1, 2, 3, 4, . . . no tiene puntos lı́mite. Ejemplo. La sucesión 1, 12 , 31 , 32 , 41 , 34 , 51 , 54 , 61 , 56 , . . . tiene 0 y 1 como puntos lı́mite. Definición. Una sucesión compleja {zn } es acotada si ∃M > 0 tal que ∀n |zn | < M . En otro caso la sucesión es no acotada. Teorema. (Teorema de Bolzano-Weierstrass.) Toda sucesión compleja acotada tiene al menos un punto lı́mite. Se demuestra usando el principio de los rectángulos encajados. (Véase la fig. 4.) 2.3. Sucesiones complejas convergentes Definición. Se dice que la sucesión compleja {zn } es convergente y tiene por lı́mite α, y se denota lı́m zn = α o bien zn → α cuando n → ∞ , (2.3) n→∞ 21 Figura 4: Construcción para el teorema Bolzano-Weierstrass. si ∀ǫ > 0 ∃ν(ǫ) tal que ∀n > ν |zn − α| < ǫ . ♦ Equivale a decir que cualquier entorno de α contiene todos los términos de la sucesión salvo un número finito de ellos. Nótese que para que {zn } sea convergente debe tener exactamente un punto lı́mite. Pero la afirmación recı́proca no es cierta. Ejemplo. La sucesión 1, 0, 2, 0, 3, 0, . . . tiene 0 como único punto lı́mite sin embargo no es convergente. Teorema. Si dos sucesiones zn → α y zn′ → α′ cuando n → ∞, entonces zn ± zn′ → α ± α′ , zn zn′ → αα′ , α zn → zn′ α′ (α′ 6= 0) . (2.4) ♦ Teorema. (Criterio de convergencia de Cauchy.) Una sucesión zn es convergente sii ∀ǫ > 0, ∃ν(ǫ) tal que |zn − zm | < ǫ siempre que n, m > ν. Definición. Decimos que lı́mn→∞ zn = ∞, o bien zn → ∞ cuando n → ∞, si ∀K > 0 ∃ν(K) tal que ∀n > ν |zn | > K. Definición. Se define un entorno del infinito (de radio R) como un conjunto {z |z| > R}, para cierto R > 0. Por tanto, zn → ∞ expresa que cualquier entorno del infinito contiene todos menos un número finito de términos de la sucesión. 22 2.4. Esfera de Riemann y plano complejo extendido La esfera de Riemann es una superficie esférica Σ ⊂ R3 (de radio arbitrario) tangente al plano complejo (C = R2 ⊂ R3 ) de modo que z = 0 coincide con el “polo sur” S de la esfera. El punto diametralmente opuesto a S es el polo norte, N . Para cualquier punto P del plano complejo se puede considerar la recta que une P y N . Dicha recta cortará Σ en otro punto P ′ . Por tanto todo número complejo z tiene asociado un punto de la esfera. Viceversa, todo punto de Σ, excepto N , tiene asociado un número complejo z. Hay una biyección entre C y Σ − {N }. (Véase la fig. 5.) N Σ P´ S P C Figura 5: Proyección estereográfica. Si lı́mn→∞ zn = ∞ los puntos correspondientes Pn′ sobre la esfera de Riemann se aproximan al polo norte, P ′ → N con n → ∞, luego se asocia N con z = ∞, llamado punto del infinito. El plano complejo junto con ∞ se llama plano complejo extendido, C∗ = C ∪ {∞}. Algunas propiedades son: z z si z ∈ C z ±∞ = ∞ , ∞z = ∞ (z 6= 0), = ∞ (z 6= 0), = 0 , ∞∞ = ∞ . (2.5) 0 ∞ Nótese que ∞ no es un elemento del plano complejo finito C. Y también que en R se suele introducir ±∞, en cambio en C sólo se introduce un único punto del infinito. La correspondencia entre el plano complejo extendido y la esfera de Riemann (incluido N ) es una biyección, denominada proyección estereográfica. El plano complejo extendido es topológicamente una esfera. Un entorno de N en la esfera de Riemann es un entorno del infinito en el plano complejo extendido. El interés de la proyección estereográfica y la esfera de Riemann es que 23 esta última es una variedad compacta (subconjunto cerrado y acotado de R3 ) y por tanto mejor comportado que R2 . 24 Funciones complejas 3. 3.1. Variables y funciones Definición. Una función compleja f (z) es una aplicación f :E → C z 7→ w = f (z) (3.1) donde E ⊂ C es el dominio de definición de f . La variable z ∈ E se llama variable independiente u original. w es la variable dependiente o imagen. El conjunto E ′ = f (E) de valores que puede tomar w se llama recorrido de f . ♦ Las mismas definiciones se aplican cuando E y E ′ son subconjuntos del plano complejo extendido. La función f puede especificarse dando los valores de u := Re w y v := Im w, f z = x + iy 7−→ w = u(x, y) + iv(x, y) (forma binómica). (3.2) Las funciones ası́ definidas son funciones univaluadas ya que para z ∈ E existe exactamente un valor w. Si se consideran correspondencias más generales donde z puede tener más de una imagen, se habla de funciones multivaluadas o multiformes. Por omisión, función se refiere a función univaluada. f : E → E′ ϕ : E′ → E , que en , se puede considerar la función inversa w 7→ z z 7→ w general será multivaluada ya que un mismo w ∈ E ′ puede ser imagen de más de un original en E. (Es decir, en general f no será inyectiva. Por construcción, f : E → E ′ es sobreyectiva.) Si ϕ es univaluada se dice que f es invertible y entonces f : E → E ′ es biyectiva. Dada una función 1 Ejemplo. f (z) = se puede definir con dominio E = C − {0} y recorrido E ′ = C − {0}. Es z 1 invertible, ϕ(w) = . En el plano complejo extendido C∗ = C ∪ {∞} se puede definir f (z) con w dominio y recorrido C∗ , tomando f (z) = 1/z si z 6= 0, ∞, f (0) = ∞, f (∞) = 0. Ejemplo. w = |z|, z ∈ C es univaluada pero no es invertible, ya que z y eiθ z (θ real) tienen igual módulo. 25 Ejemplo. f : C → C con f (z) = z 2 es univaluada pero no invertible, su inversa ϕ es bivaluada (excepto si z = 0) ya que ±z → z 2 . Ejemplo. f : E → C siendo f (z) = z 2 y E = {z Re (z) > 0, Im (z) > 0} (es decir, z es un punto del primer cuadrante). f (z) es inyectiva ya que si z ∈ E, −z 6∈ E. Su recorrido es E ′ = {w Im (w) > 0}. En efecto, z = reiθ ∈ E sii r > 0 y 0 < θ < π/2. Entonces, w = ρeiφ = z 2 tiene ρ = r2 > 0 y 0 < φ = 2θ < π, y por tanto w es un punto cualquiera de E ′ . f : E → E ′ es invertible. 3.2. Curvas y dominios Definición. (Curva orientada.) Sean x(t), y(t) dos funciones reales y continuas de la variable real t con a ≤ t ≤ b. La aplicación z(t) = x(t) + iy(t) es un camino en el plano complejo. z(a) y z(b) son el punto inicial y el punto final, respectivamente. El conjunto de todos los caminos con el mismo recorrido y el mismo punto inicial y el mismo punto final define una curva orientada (continua) C. Por tanto, a cada curva C le corresponden infinidad de caminos, y cada camino define una parametrización de la curva. El sentido positivo13 de C se obtiene cuando t va de a a b. Definición. Si z(a) = z(b) se dice que la curva es cerrada, en otro caso es una curva abierta o arco. Definición. Un conjunto de puntos E se dice que es (arco-) conexo si cualquier par de puntos z1 , z2 ∈ E puede unirse mediante un arco C contenido en E con z1 y z2 como puntos inicial y final. Definición. Dado un conjunto E se dice que z es un punto interior de E si E contiene algún entorno de z (en particular z ∈ E). Se dice que E es abierto si todos sus puntos son interiores. Se dice que E es cerrado si su complementario, E c = C − E, es abierto. Ejemplo. El conjunto14 {0 < |z| < 1} es abierto, {|z| ≤ 1} es cerrado, {0 < |z| ≤ 1} no es abierto ni cerrado. Definición. Un conjunto no vacı́o G es un dominio si es abierto y conexo. (No debe confundirse este concepto con el de dominio de definición de una función.) Definición. Un dominio G (o en general un conjunto E) es acotado si está contenido en un entorno de cero, es decir, si ∃K > 0 tal que ∀z ∈ E, |z| < K. En otro caso es no acotado. 13 14 El sentido positivo para el caso especial de una curva cerrada simple se define más adelante. Para aligerar la notación usamos {0 < |z| < 1} para indicar el conjunto {z 0 < |z| < 1}, etc. 26 Definición. Se dice que z es un punto exterior de E cuando z es un punto interior del complementario de E. Los puntos que no son interiores ni exteriores a E son puntos frontera de E. El conjunto de puntos frontera es la frontera de E. Se dice que z es un punto de acumulación o punto lı́mite de E si en todo entorno de z hay infinitos puntos de E. Ejemplo. Sea E = {0 < |z| < 1} ∪ {2}. Sus puntos interiores son {0 < |z| < 1}. Sus puntos exteriores son {1 < |z|, z 6= 2}. Su frontera es {0, 2} ∪ {|z| = 1}. Su puntos de acumulación son {|z| ≤ 1}. Proposición. Todos los dominios tienen una frontera no vacı́a excepto C. Proposición. Un conjunto es cerrado sii contiene su frontera. Un conjunto es cerrado sii contiene a todos sus puntos de acumulación. Definición. Un dominio G junto con ninguno, alguno o todos sus puntos frontera se denomina una región, G̃. Un dominio es una región abierta. Un dominio junto con su frontera es una región cerrada, Ḡ. Ejemplo. Una curva no es una región: todos sus puntos son de la frontera, y si se quita ésta queda el conjunto vacı́o, que no es un dominio. Definición. Una curva es simple o de Jordan, si no pasa dos veces por el mismo punto de C (no se corta a sı́ misma), es decir, si a ≤ t1 < t2 < b implica z(t1 ) 6= z(t2 ). Teorema. (Teorema de la curva de Jordan.) Toda curva simple cerrada C divide el plano complejo finito en dos dominios de los que C es frontera común. Uno de ellos es acotado (llamado interior de C) y el otro no acotado (llamado exterior de C). Definición. Se toma el sentido positivo de una curva simple cerrada de modo que su interior esté localmente a la izquierda de la curva (para un observador que recorra la curva). Coincide con el sentido antihorario. Definición. En el plano complejo finito, se dice que un dominio G es simplemente conexo si toda curva simple cerrada contenida en G tiene su interior también contenido en G. En el plano complejo extendido se dice que G es simplemente conexo si para toda curva cerrada simple su interior o su exterior están contenidos completamente contenidos en el dominio G. En otro caso G es múltiplemente conexo. Ejemplo. El dominio G1 = {|z| < r} es simplemente conexo. G2 = {r < |z|} (r ≥ 0) no 27 C0 C1 G C2 C3 Figura 6: Dominio (n + 1)-conexo (n = 3). es simplemente conexo en C (pero si en C∗ ). En efecto, una circunferencia de radio ρ > r tiene z = 0 6∈ G2 en su interior. G3 = {r < |z| < R} (0 ≤ r < R) no es simplemente conexo ni en C ni en C∗ . Definición. Si C0 , C1 , . . . , Cn son n+1 curvas cerradas simples tales que cada curva C1 , C2 , . . . , Cn está en el interior de C0 y en el exterior de las demás, entonces el conjunto formado por los puntos que son del interior de C0 y del exterior de C1 , C2 , . . . , Cn , forman un dominio G cuya frontera está formada por la n + 1 curvas C0 , C1 , . . . , Cn . (Véase la fig. 6.) Si n = 0, G0 es simplemente conexo. Si n > 0 Gn no es simplemente conexo, se dice que es (n + 1)-conexo. 3.3. Continuidad de funciones complejas Definición. Sea G un dominio (región abierta) y z0 ∈ G, y sea f (z) una función compleja definida en G − {z0 } (la función puede estar definida en z0 o no). Se dice que f (z) tiene lı́mite α cuando z → z0 , y se denota lı́m f (z) = α , (3.3) z→z0 si ∀ǫ > 0, ∃δ(ǫ, z0 ) > 0 tal que 0 < |z − z0 | < δ garantiza |f (z) − α| < ǫ. (Véase la figura 7.) Ejemplo. Sea f : C → C tal que f (0) = 1 y f (z) = 0 ∀z 6= 0. En este caso lı́mz→0 f (z) = 0. Nótese que no habrı́a lı́mite si en la definición se exigiera |f (z) − α| < ǫ ∀z |z − z0 | < δ, sin excluir el caso z = z0 . Definición. f (z) es continua en z0 si f (z0 ) 6= ∞ y además lı́m f (z) = f (z0 ) , z→z0 28 (3.4) z w G ε w=f(z) δ z α 0 Figura 7: La imagen del entorno de z0 de tamaño δ, en el plano z, está contenido en el entorno de α de tamaño ǫ en el plano w = f (z). es decir, si ∀ǫ > 0, ∃δ(ǫ, z0 ) > 0 tal que |z − z0 | < δ garantiza |f (z) − f (z0 )| < ǫ.15 Ejemplo. f (z) = 1/z definida en el plano complejo extendido no es continua en z = 0 aunque lı́mz→0 f (z) = f (0) ya que f (0) = ∞. Definición. La función f es continua en G (en sentido puntual) si es continua en todo punto de G. Ejemplo. w = 1/z es continua en todo el plano complejo excepto en z = 0: En efecto, sea z0 6= 0 el punto en el que queremos ver que la función 1/z es continua, y tomemos δ < 12 |z0 |, de modo que para cualquier punto z en el disco |z − z0 | < δ se tiene que |z| > 12 |z0 |. Para la imagen del disco se tiene entonces 1 |z − z0 | 1 2δ |w − w0 | = − = < , (3.5) z z0 |z||z0 | |z0 |2 magnitud que puede hacerse menor que cualquier ǫ > 0 eligiendo δ < 21 ǫ|z0 |2 (además de δ < 12 |z0 |). ♦ Proposición. Si f (z) y g(z) son continuas en z0 , también lo son las funciones f (z) ± g(z), f (z)g(z) y f (z)/g(z) (si g(z0 ) 6= 0). Si ϕ(w) es continua en w0 = f (z0 ), ϕ(f (z)) es continua en z0 . Cuando f (z) está definida en una región G̃ y z0 es de la frontera de G̃ no está garantizado que z ∈ G̃ si |z − z0 | < δ (δ suficientemente pequeño). En este caso hay que cambiar la definición 15 En este caso, exigir |f (z) − f (z0 )| < ǫ también para z = z0 es irrelevante. No impone ninguna restricción. 29 añadiendo la condición z ∈ G̃. Se denota lı́m f (z) = α , z → z0 z ∈ G̃ lı́m f (z) = f (z0 ) . z → z0 z ∈ G̃ (3.6) para indicar lı́mite y continuidad, respectivamente. Análogamente, si f (z) está definida sobre una curva C lı́m f (z) = α , lı́m f (z) = f (z0 ) . (3.7) z → z0 z → z0 z∈C z∈C Definición. La expresión lı́mz→z0 f (z) = ∞ significa lı́m z→z0 1 = 0. f (z) (3.8) O equivalentemente, ∀K > 0, ∃δ > 0 tal que 0 < |z − z0 | < δ implica |f (z)| > K. La expresión lı́mz→∞ f (z) = α significa lı́m f (1/ζ) = α . ζ→0 (3.9) O equivalentemente, ∀ǫ > 0, ∃R > 0 tal que |z| > R implica |f (z) − α| < ǫ. ♦ Estad definiciones corresponden a la definición usual de lı́mite desde el punto de vista de la esfera de Riemann de las variables w o z, respectivamente. 3.4. Continuidad uniforme Definición. Una función f (z) definida en un dominio G es uniformemente continua en G si y sólo si ∀ǫ > 0 ∃δ(ǫ) > 0 tal que para todo par de puntos z1 , z2 ∈ G, la condición |z1 − z2 | < δ garantiza |f (z1 ) − f (z2 )| < ǫ . (3.10) La misma definición se aplica cuando f esté definida en una región G̃ o una curva C, imponiendo z1 , z2 ∈ G̃ o C, respectivamente. 30 Nota: El punto clave es que δ depende sólo ǫ (aparte de f y G), pero no de z1 , z2 . Esta condición es más fuerte (exigente) que la continuidad en un punto z0 ∈ G ya que ahı́ δ podı́a depender de z0 . Proposición. Continuidad uniforme implica continuidad en cada punto (pero no al contrario). Ejemplo. La función f (z) = 1/z definida en G̃ = {0 < |z| ≤ 1} es continua en G̃ pero no uniformemente continua: En efecto, la condición |z1 − z2 | < δ para z1 , z2 ∈ G̃, no garantiza que |z1−1 − z2−1 | < ǫ. Por ejemplo, tomando z1 = δ/2 y z2 = δ, se cumple |z1 − z2 | < δ, pero |z1−1 − z2−1 | = 1/δ que no es arbitrariamente pequeño (todo lo contrario). Definición. Un conjunto es compacto cuando es cerrado y acotado. Ejemplo. Una curva es un conjunto compacto (es decir, cerrado y acotado).16 Un disco cerrado es un conjunto compacto. C no es compacto, porque aunque es cerrado, no es acotado. Teorema. (Teorema de Heine-Borel.) Un conjunto compacto (cerrado y acotado) Ḡ con un recubrimiento {Cα } admite un subrecubrimiento finito.17 Teorema. Si f (z) es continua en una región compacta (cerrada y acotada) Ḡ, entonces f es uniformemente continua en Ḡ y acotada. Este teorema se puede demostrar mediante el teorema de Heine-Borel. (Ver por ejemplo el libro de Silverman.) Ejemplo. En el ejemplo anterior, la función f (z) = 1/z definida en G̃ = {0 < |z| ≤ 1} era continua en G̃ pero no uniformemente continua. El teorema no se aplica porque G̃ es acotado pero no cerrado (z = 0 es de la frontera pero no del conjunto). f (z) tampoco está acotada en G̃: En efecto, lı́mz→0 1/z = ∞. Ejemplo. f (z) = z es continua en C y uniformemente continua en C, pero no acotada. Ejemplo. f (z) = z 2 es continua en C pero no uniformemente continua ni acotada en C. 16 La imagen de un conjunto compacto por una aplicación continua es a su vez un conjunto compacto. En topologı́as generales esto se toma como definición de conjunto compacto. En ese caso el teorema afirma que un subconjunto de Rn es compacto sii es un conjunto cerrado y acotado. 17 31 Derivación en el plano complejo 4. 4.1. Derivada de una función compleja Definición. (Derivada compleja.) Una función compleja f (z) definida en un dominio G se dice que es derivable o diferenciable en el punto z ∈ G si f (z) 6= ∞ y el lı́mite f (z + ∆z) − f (z) , ∆z→0 ∆z f ′ (z) := lı́m z, z + ∆z ∈ G existe y es finito. f ′ (z) se llama derivada de f (z) en z. También se denota (4.1) df (z) . dz Nótese que una función compleja derivable en un punto es necesariamente continua en ese punto (aunque no al revés). Definición. (Función analı́tica.) Una función f (z) es analı́tica en un dominio G (o también regular u holomorfa) si es derivable en cada punto de G. Se dice que es analı́tica en un punto z si lo es algún entorno de z. Todo punto de C en el que f (z) es analı́tica es un punto regular de f (z). Todo punto de C en el que f (z) no sea analı́tica (en particular, si no está definida ahı́) es un punto singular de f (z). Ejemplo. f (z) = z 2 es derivable en todos los puntos del plano complejo (finito): (z + ∆z)2 − z 2 = lı́m (2z + ∆z) = 2z . f (z) = lı́m ∆z→0 ∆z→0 ∆z ′ (4.2) Ejemplo. f (z) = Re (z) es continua en todo el plano complejo pero no derivable en ningún punto: Re (z + ∆z) − Re (z) Re ∆z lı́m = lı́m . (4.3) ∆z→0 ∆z→0 ∆z ∆z Teniendo en cuenta que ∆z = ∆x + i∆y, se ve que si se hace el lı́mite según ∆y = 0, ∆x → 0 sale 1, en cambio si se hace el lı́mite según ∆x = 0, ∆y → 0 sale 0. Luego el lı́mite no existe y la función no es derivable. Ejemplo. Igualmente f (z) = z ∗ es continua en todo el plano complejo pero no derivable en ningún punto. 32 Ejemplo. f (z) = |z|2 es derivable en z = 0 pero no en ningún otro punto. Por tanto no es analı́tica en ningún punto. Nota: La condición de derivabilidad en el plano complejo exige que el lı́mite ∆f /∆z sea independiente de la dirección en la que ∆z → 0. La condición de analiticidad es aún más restrictiva, como se ha visto en el último ejemplo. Propiedades. Como la definición de f ′ (z) es algebraicamente idéntica a la del caso real, satisface las siguientes propiedades: a) (c f (z))′ = c f ′ (z), donde c es una constante y f (z) es derivable en z. b) Si f (z) y g(z) son derivables en z, (f (z) ± g(z))′ = f ′ (z) ± g ′ (z) (f (z)g(z))′ = f ′ (z)g(z) + f (z)g ′ (z) ′ f ′ (z) f (z)g ′ (z) f (z) − (g(z) 6= 0) . = g(z) g(z) g 2 (z) (4.4) c) Si f (z) es derivable en z y ϕ(w) es derivable en w = f (z) (ϕ(f (z)))′ = ϕ′ (f (z))f ′ (z) . d) (z n )′ = nz n−1 , (4.5) n = 1, 2, , 3, . . . Proposición. Todo polinomio de z, P (z) = n X ak z k , k=0 ak ∈ C (4.6) es analı́tico en todo el plano complejo (finito) y toda función racional (cociente de polinomios de z) es analı́tica en todo el plano complejo excepto donde el denominador se anule. Nota: Sin embargo los polinomios o funciones racionales construidas con z y z ∗ no son funciones analı́ticas en ningún punto (a menos que no dependan de z ∗ ). (Veánse los complementos al final del capı́tulo.) Definición. (Diferenciales complejos.) Sea f (z) derivable en un punto z, y w = f (z), definimos el incremento de f (z) como ∆w := f (z + ∆z) − f (z) , (4.7) 33 considerado como función de ∆z. Puesto que ∆w = f ′ (z) ∆z→0 ∆z lı́m (4.8) se deduce ∆w = f ′ (z)∆z + ǫ∆z , donde lı́m ǫ = 0 . ∆z→0 (4.9) La parte lineal, f ′ (z)∆z, se denomina diferencial de w y se denota dw, dw = f ′ (z)∆z. Teniendo en cuenta que en particular dz = ∆z (considerando z como función de la propia z), dw = f ′ (z) dz, 4.2. f ′ (z) = dw df (z) = . dz dz (4.10) Las ecuaciones de Cauchy-Riemann Definición. Una función real u(x, y) es derivable o diferenciable en (x, y) si el incremento ∆u = u(x + ∆x, y + ∆y) − u(x, y) (4.11) (considerado como función de las variables independientes ∆x y ∆y) puede escribirse como ∆u = A1 ∆x + A2 ∆y + ǫ1 ∆x + ǫ2 ∆y (4.12) donde A1 , A2 no dependen de ∆x, ∆y y ǫ1 , ǫ2 → 0 cuando ∆x, ∆y → 0.18 De hecho A1 y A2 son las derivadas parciales de u: ∂u ∂u A1 = , A2 = .♦ (4.13) ∂x (x,y) ∂y (x,y) p Nota: Que ∂u/∂x y ∂u/∂y existan no basta para que u sea diferenciable. (Por ejemplo u = |xy| tiene derivadas parciales en x = y = 0 pero no es diferenciable en ese punto.) Una condición suficiente para sea diferenciable es que tenga derivadas parciales y que sean continuas. Una función compleja f (z) puede especificarse dando sus partes real e imaginaria f (z) = u(x, y) + iv(x, y) , 18 u, v ∈ R . (4.14) Es decir, ǫ1,2 → 0 cuando (∆x)2 + (∆y)2 → 0, independientemente de la dirección en el plano x, y. Nótese también que ǫ1,2 no quedan definidos en forma unı́voca por la ecuación. 34 Si u, v son continuas, f también lo será (y viceversa). En cambio, como se vio para f (z) = Re (z), que corresponde a u(x, y) = x, v(x, y) = 0, obviamente u, v son diferenciables pero u + iv no es diferenciable como función compleja. En general u y v deben además estar relacionados. En efecto, si f (z) es derivable en z el lı́mite de ∆w/∆z no debe depender de la dirección en la que ∆z → 0. En particular debe dar lo mismo si va a 0 por el eje real o por el imaginario: ∆u + i∆v ∂u ∂v ∆u + i∆v = lı́m = +i lı́m ∆x ∂x ∂x ∆x → 0 ∆x + i∆y ∆x→0 ∆y = 0 ∆u + i∆v ∆u + i∆v 1 ∂u ∂v ′ f (z) = lı́m = lı́m = +i i∆y i ∂y ∂y ∆y → 0 ∆x + i∆y ∆y→0 ∆x = 0 f ′ (z) = (4.15) ∂u ∂v ∂u ∂v = , = − , conocidas como ecuaciones de Cauchy-Riemann. Podrı́a ∂x ∂y ∂y ∂x pensarse que el cálculo de f ′ (z) tomando el lı́mite según otras direcciones da nuevas condiciones. No es ası́, como lo demuestra el siguiente teorema: requiere Teorema. (Ecuaciones de Cauchy-Riemann.) La función compleja w = f (z) = u + iv es derivable en el punto z0 = x0 + iy0 si y sólo si 1) u(x, y), v(x, y) son diferenciables en (x0 , y0 ). 2) Cumplen las ecuaciones de Cauchy-Riemann, ∂v ∂u = , ∂x ∂y ∂u ∂v =− , ∂y ∂x en (x0 , y0 ). (4.16) con (4.17) Demostración: a) Supongamos que f (z) es derivable en z0 , es decir, ∆w = ∆u + i∆v = f ′ (z)∆z + ǫ∆z , lı́m ǫ = 0 , ∆z→0 f ′ (z) = a + ib (a, b reales) y ǫ = ǫ1 + iǫ2 (ǫ1,2 reales). Entonces ∆u + i∆v = (a + ib)(∆x + i∆y) + (ǫ1 + iǫ2 )(∆x + i∆y) implica ∆u = a∆x − b∆y + ǫ1 ∆x − ǫ2 ∆y , ∆v = b∆x + a∆y + ǫ2 ∆x + ǫ1 ∆y . 35 (4.18) Teniendo en cuenta que ǫ1 , ǫ2 → 0 cuando ∆x, ∆y → 0, se deduce u, v son diferenciables y a= ∂v ∂u = , ∂x ∂y b= ∂u ∂v =− . ∂y ∂x (4.19) b) Supongamos que u, v cumplen 1) y 2), entonces: ∂u ∂u ∆x + ∆y + α1 ∆x + α2 ∆y ∆w = ∆u + i∆v = ∂x ∂y ∂v ∂v +i ∆x + ∆y + β1 ∆x + β2 ∆y ∂x ∂y ∂u ∂v = (∆x + i∆y) + (α1 + iβ1 )∆x + (α2 + iβ2 )∆y +i ∂x ∂x ∂v ∆y ∆x ∂u +i + (α2 + iβ2 ) .(4.20) ∆z + ǫ∆z , con ǫ = (α1 + iβ1 ) = ∂x ∂x ∆z ∆z Puesto que |∆x|, |∆y| ≤ |∆z|, se deduce |ǫ| ≤ |α1 | + |β1 | + |α2 | + |β2 | → 0 cuando ∆z → 0 . (4.21) En consecuencia, el lı́mite ∆w ∂u ∂v = +i ∆z→0 ∆z ∂x ∂x f ′ (z0 ) = lı́m (4.22) existe y es finito y f (z) es derivable en z0 . ♦ Proposición. f (z) es analı́tica en un dominio G sii u, v son diferenciables y ux = vy , uy = −vx en todo G. En este caso f ′ (z) = ux + ivx = ux − iuy = vy + ivx = vy − iuy , z ∈ G. (4.23) Ejemplo. La función ez := ex (cos(y) + i sen(y)) es la exponencial compleja. Extiende la función exponencial real al plano complejo. Es diferenciable en todo C y también satisface las ecuaciones de Cauchy-Riemann. Por tanto es analı́tica en C. Su derivada coincide con ella misma, como ocurre en el caso real. Definición. (Función analı́tica en el infinito.) Se dice que f (z) es analı́tica en el infinito si la función ϕ(ζ) = f (1/ζ) es analı́tica en ζ = 0. Se define f (∞) = ϕ(0). 36 Definición. Si f (z) = u + iv es analı́tica en un dominio G, f ′′ (z) existe y es continua (como se verá) y además ux = vy , uy = −vx . Se deduce entonces que u y v son funciones armónicas, es decir, 2 2 ∂ ∂ ∂2 ∂2 u= v = 0. (4.24) + + ∂x2 ∂y 2 ∂x2 ∂y 2 En efecto,19 uxx + uyy = (vy )x + (−vx )y = 0 (ı́dem v). Se dice que u y v son funciones armónicas conjugadas si tienen derivadas parciales segundas continuas y cumplen las ecuaciones de CauchyRiemann. Ejemplo. f (z) = z 3 es una función analı́tica en C. u = x3 − 3xy 2 , v = 3x2 y − y 3 , ux = vy = 3x2 − 3y 2 , uy = −vx = −6xy , uxx = −uyy = 6x , vxx = −vyy = 6y . (4.25) Como se ha visto (z 3 )′ = 3z 2 . Alternativamente, f ′ (z) = ∂f = ux + ivx = (3x2 − 3y 2 ) + i(6xy) = 3z 2 . ♦ ∂x (4.26) Si u, v son armónicas conjugadas se puede reconstruir una en función de otra. Por ejemplo Z y v(x, y) = v(x, y0 ) + vy (x, y ′ ) dy ′ Zy0 x Z y ′ ′ = v(x0 , y0 ) + vx (x , y0 ) dx + vy (x, y ′ ) dy ′ Zx0x Zy0y = v(x0 , y0 ) − uy (x′ , y0 ) dx′ + ux (x, y ′ ) dy ′ . (4.27) x0 y0 Esta construcción supone que el camino (x0 , y0 ) → (x, y0 ) → (x, y) está contenido en la región G de validez de las ecuaciones de Cauchy-Riemann. En realidad si u, v existen (son univaluadas) en un dominio G y son armónicas conjugadas, el resultado no depende de la curva suave a trozos C (con punto inicial (x0 , y0 ) y final (x, y) y contenida en G): Z Z v(x, y) − v(x0 , y0 ) = (vx dx + vy dy) = (−uy dx + ux dy) . (4.28) C 19 C Si una función u tiene derivadas parciales segundas continuas automáticamente uxy = uyx . 37 Por otro lado, si G es simplemente conexo esta fórmula permite reconstruir v conocido u. (Obviamente hay una fórmula análoga para reconstruir u dado v.) Teorema. (Regla de l’Hôpital.) Sean f (z), g(z) analı́ticas en un entorno de z0 ∈ C∗ = C∪{∞}. Si f (z), g(z) tienden ambas a 0 o ∞ cuando z → z0 y si f ′ (z)/g ′ (z) tiene lı́mite (finito o no) éste coincide con el lı́mite de f (z)/g(z), que existe. Este teorema se aplica y demuestra igual que en el caso real. ez ez − 1 1 = lı́m = . z→0 2 z→0 2z 2 Ejemplo. lı́m Nota: Una función real definida en R2 puede ser diferenciable 2en un dominio pero no admitir dex si x > 0 rivadas segundas continuas. (Por ejemplo, la función h(x, y) = .) O bien puede admitir 0 si x ≤ 0 un número finito de derivadas continuas pero no un número infinito. O bien puede admitir −1/x un número e si x > 0 infinito de derivadas continuas pero no ser analı́tica.20 (Por ejemplo, h(x, y) = . 0 si x ≤ 0 Todas las derivadas de todos los órdenes de esta función se anulan en el punto (0, 0), sin embargo la función no es idénticamente nula en un entorno de ese punto y por tanto la función no es analı́tica ahı́.) Para una función definida sobre R2 las propiedades de ser derivable una vez, derivable k veces, derivable infinitas veces y analı́tica son condiciones cada vez más fuertes (restrictivas). En cambio en el caso complejo se ha denominado analı́tica a un función por el hecho de tener derivada primera en un dominio. Como se verá, esta denominación está justificada: si una función compleja admite derivada primera en un dominio entonces automáticamente es también infinitamente derivable y analı́tica en el sentido de R2 en ese dominio. Este resultado es muy notable. 4.3. Complementos Definición. Una función de varias variables complejas w = f (z1 , . . . , zn ) es derivable o diferenciable si satisface unas condiciones análogas a las dadas para variables reales. A saber, ∆w = f (z1 + ∆z1 , . . . , zn + ∆zn ) − f (z1 , . . . , zn ) = (A1 + ǫ1 )∆z1 + · · · + (An + ǫn )∆zn (4.29) donde los Ak no dependen de ∆z1 , . . . , ∆zn y los ǫk → 0 cuando ∆z1 , . . . , ∆zn → 0. Los Ak son 20 En Rn una función es analı́tica si admite un desarrollo en serie de Taylor con radio de convergencia no nulo. 38 las derivadas parciales de f en (z1 , . . . , zn ): Ak = ∂f .♦ ∂zk (4.30) Proposición. Sea g(z1 , z2 ) una función compleja de dos variables, analı́tica (respecto de z1 y z2 ) en un dominio G12 ⊂ C × C, y sea f (z) la función definida por f (z) = g(z, z ∗ ). Entonces, f (z) es analı́tica en el dominio G = {z (z, z ∗ ) ∈ G12 } (supuesto no vacı́o) sii g(z1 , z2 ) es independiente de z2 . Demostración: Puesto que g(z1 , z2 ) es diferenciable, el incremento de f (z) para z ∈ G puede escribirse como ∆f (z) = ∆g(z, z ∗ ) = g(z + ∆z, z ∗ + ∆z ∗ ) − g(z, z ∗ ) = g1 ∆z + g2 ∆z ∗ + ǫ∆z + ǫ′ ∆z ∗ (4.31) donde g1,2 son las derivadas parciales de g respecto de z1 y z2 en z1 = z2∗ = z, y ǫ, ǫ′ se anulan cuando ∆z → 0. Entonces ∆z ∗ ∆z ∗ ∆f (z) = g1 + g2 + ǫ + ǫ′ . ∆z ∆z ∆z (4.32) Teniendo en cuenta que |∆z ∗ /∆z| = 1 se ve que los términos con ǫ, ǫ′ se anulan cuando ∆z → 0, y para que el lı́mite exista (independientemente de la dirección de ∆z) es necesario y suficiente que g2 se anule ∂g(z1 , z2 ) = 0 cuando z1 = z2∗ = z . ♦ (4.33) ∂z2 Ejemplo. La función z n depende de z y no de z ∗ ; satisface las ecuaciones de Cauchy-Riemann (y de hecho es analı́tica para todo z excepto en z = 0 si n < 0). √ En cambio Re (z) = (z + z ∗ )/2 depende de z ∗ y no las puede satisfacer. Igualmente f (z) = |z| = zz ∗ no es analı́tica. Nota: Usando las relaciones x= z + z∗ , 2 y= z − z∗ , 2i (4.34) cualquier función racional de x, y se puede expresar como función de z y z ∗ . En este caso la función será analı́tica (donde el denominador no se anule) sii no depende de z ∗ . El cambio de variable también es aplicable a funciones definidas por series de potencias de x, y. 39 Integración en el plano complejo 5. 5.1. La integral de una función compleja Definición. Una curva C con ecuación paramétrica z = z(t) (a ≤ t ≤ b) es suave sii z(t) tiene derivada continua y no nula (ż(t) 6= 0) ∀t ∈ [a, b]. (En los extremos ż(a) se refiere a derivada por la derecha y ż(b) a derivada por la izquierda.) Definición. Sean C1 , C2 , . . . , Cn un conjunto finito de curvas suaves tales que el punto final de Ck es el punto inicial de Ck+1 , para k = 1, . . . , n − 1. La curva C obtenida uniendo dichas curvas se denomina curva suave a trozos. Proposición. Una curva suave a trozos es rectificable (es decir, tiene longitud finita). Demostración: En efecto, la longitud de C es Z b ℓ= |ż(t)| dt < ∞ . (5.1) a ℓ es finita porque ż(t) es continua a trozos y por tanto integrable Riemann. ♦ Definición. (Integral en C.) Sea f (z) una función definida en un dominio G y C una curva suave contenida en G, con puntos inicial y final za y zb . Si z0 , z1 , . . . , zn con z0 = za , zn = zb , es un conjunto de puntos de C ordenados por t creciente (correspondientes as a = t0 < t1 < · · · < tn = b), consideremos la suma n X S= f (ζk )∆zk (5.2) k=1 ⌢ donde ∆zk = zk − zk−1 y ζk es un punto arbitrario del arco zk−1 zk . Sea ℓk la longitud del arco ⌢ zk−1 zk y λ = máx{ℓ1 , . . . , ℓn }, si el lı́mite lı́m λ→0 n X f (ζk )∆zk (5.3) k=1 existe y es finito, se dice que f (z) es integrable a lo largo de C y al lı́mite se le llama integral de f (z) a lo largo de C, y se denota Z f (z) dz . ♦ (5.4) C 40 Notas: 1) La integral depende de C y de la orientación de la curva. Cuando se diga curva se entenderá curva orientada. 2) La integral, tal y como se ha definido, no depende de la parametrización usada para la curva. (La parametrización debe consistente con la orientación de la curva.) 3) Como se puede ver, si f (z) es real y C es un intervalo real, la integral que se ha definido coincide con la integral de Riemann usual. Las siguientes manipulaciones son válidas Z Z Z Z f (z) dz = (u + iv) (dx + idy) = (u dx − v dy) + i (v dx + u dy) C C C (5.5) C entendidas como integrales reales de lı́nea en R2 . Y también Z b Z b Z Z b dz(t) dt = Re f (z(t))ż(t) dt + i Im f (z(t))ż(t) dt , f (z) dz = f (z(t)) dt a a C a (5.6) donde z(t) es cualquier parametrización con sentido positivo de C.21 Por tanto basta calcular integrales reales usuales. La integral compleja existe si y sólo si las correspondientes integrales reales existen. 1 Ejemplo. Calcúlese la integral de f (z) = a lo largo del segmento recto C que empieza en z z = 1 y acaba en z = i. El segmento admite la parametrización z(t) = 1+(i−1)t, 0 ≤ t ≤ 1, con ż(t) = i−1. Entonces Z Z 1 1 (i − 1) dt f (z) dz = C 0 1 + (i − 1)t Z 1 Z 1 2t − 1 iπ 1 = dt + i dt = .♦ (5.7) 2 2 2 0 1 − 2t + 2t 0 1 − 2t + 2t Teorema. Si f (z) es continua sobre una curva suave C entonces es integrable en C. Es una consecuencia inmediata de la misma propiedad para integrales reales de lı́nea ya que ż(t) también es continua por tratarse de una curva suave. La definición de integral se extiende al caso de curvas suaves a trozos. La integral en C = C1 ∪ C2 ∪ · · · ∪ Cn se define Z Z Z f (z) dz = f (z) dz + · · · + f (z) dz , (5.8) C 21 C1 Cn En efecto, si t = t(s) es una reparametrización positiva de la curva 41 dz(t) dz(t(s))/ds dt(s) dz(t(s)) dt = ds = ds. dt dt(s)/ds ds ds que es compatible con la definición anterior cuando C es ella misma suave. R Ejemplo. Calcúlese C z n dz donde C es una curva suave a trozos que une za con zb (puntos inicial y final), n ∈ Z, n 6= −1, y C no pasa por z = 0 si n < 0 (en otro caso f (z) = z n no serı́a continua sobre C). Primero lo hacemos para C suave: Z b Z Z b 1 n+1 d n n z (t) dt z (t) ż(t) dt = z dz = n+1 a dt a C b 1 1 n+1 = z (t) dt = zbn+1 − zan+1 , (n 6= −1) . (5.9) n+1 n+1 a Esta integral no depende de C sino sólo de za y zb . Cuando C es suave a trozos se aplica el resultado anterior a cada trozo y se suma, y se obtiene exactamente la misma expresión. En particular, se obtiene Z z n dz = 0 (C cerrada, n entero y 6= −1) C (5.10) si C es cualquier curva suave a trozos cerrada (que no pase por 0 si n < 0). 5.2. Propiedades básicas de la integral Definición. Si C es una curva suave a trozos, definimos C − como la curva C orientada al revés, es decir, C − recorre los mismos puntos pero el punto final de C es el inicial de C − y viceversa. Teorema. Si f (z) es integrable sobre C entonces Z Z f (z) dz = − f (z) dz . C− (5.11) C Es inmediato notando que ∆zk → −∆zk con C → C − mientras que f (ζk ) no cambia. Teorema. Si f y g son integrables sobre C y α, β ∈ C Z Z Z α f (z) + β g(z) dz = α f (z) dz + β g(z) dz . C C (5.12) C Teorema. Sea f (z) integrable sobre una curva suave a trozos C y acotada en C (es decir, ∃K tal que ∀z ∈ C |f (z)| < K) entonces Z f (z) dz ≤ Kℓ , (5.13) C 42 siendo ℓ la longitud de C. Demostración: n n n X X X f (ζk )∆zk ≤ |f (ζk )| |∆zk | ≤ K |∆zk | ≤ Kℓ . ♦ k=1 5.3. k=1 (5.14) k=1 Teorema de la integral de Cauchy Éste es uno de los teoremas clave del análisis complejo: Teorema. (Teorema de la integral de Cauchy.) Sea f (z) analı́tica en un dominio G simplemente conexo (en el plano finito) y sea C una curva suave a trozos y cerrada contenida en G, entonces Z f (z) dz = 0 . (5.15) C Se puede dar una versión más fuerte: Teorema. (Teorema generalizado de la integral de Cauchy.) Sea C una curva simple, suave a trozos y cerrada, y sea f (z) analı́tica en el interior de C (I(C)) y continua en I(C) ∪ C, entonces Z f (z) dz = 0 . (5.16) C Esta versión es más fuerte porque no se requiere que f (z) sea analı́tica sobre la curva sino sólo continua. Por otro lado se exige que C sea simple pero esto no es una restricción ya que si C no es simple se puede descomponer en curvas cerradas que lo sean.22 (Véase la fig. 8.) Aquı́ se demostrará una versión mucho más débil del teorema de la integral de Cauchy en el que se pide además que f ′ (z) sea continua en G. (Como se verá esta condición es redundante.) Como se ha visto, sin pérdida de generalidad se puede suponer que C es simple. En este caso se puede aplicar el teorema de Green: 22 El motivo de no quitar la palabra “simple” en el enunciado es que sólo se ha definido el interior para curvas cerradas simples. 43 C2 G G C C3 C1 Figura 8: Descomposición de una curva (C, a la izquierda) en curvas simples (C1 , C2 y C3 , a la derecha). A efectos de integración C1 ∪ C2 ∪ C3 es equivalente a C. Teorema. (Teorema de Green.) Sean P (x, y) y Q(x, y) con derivadas parciales continuas sobre la curva C (simple, cerrada y suave a trozos) ası́ como en el interior de C, entonces Z ZZ ∂Q ∂P − dx dy , (5.17) (P dx + Q dy) = ∂x ∂y C I donde C está orientado positivamente e I es el interior de C. 23 Demostración: (Teorema de la integral de Cauchy. Versión débil.) En efecto, si u, v tienen derivadas parciales continuas, Z Z Z f (z) dz = (u dx − v dy) + i (v dx + u dy) C C C ZZ ZZ ∂u ∂v ∂v ∂u dx dy + i dx dy = 0 , (5.18) − − − = ∂x ∂y ∂x ∂y G G haciendo uso de las ecuaciones de Cauchy-Riemann. ♦ Proposición. Sea f (z) analı́tica en un dominio simplemente conexo G y sean C1 y C2 dos arcos suaves a trozos contenidos en G con el mismo punto inicial y el mismo punto final, entonces las integrales sobre C1,2 son iguales: Z Z f (z) dz = f (z) dz . (5.19) C1 C2 Demostración: En efecto, por aplicación del teorema de la integral de Cauchy a la curva cerrada C1 ∪ C2− . (Véase la fig. 9.) R R ~·∇×A ~ en R3 , tomando A ~ = (P (x, y), Q(x, y), 0), ~ = dS Esta es una versión bidimensional de C d~ℓ · A S ~ = (∂y Az − ∂z Ay , ∂z Ax − ∂x Az , ∂x Ay − ∂y Ax ) = (0, 0, ∂x Q − ∂y P ) y dS ~ = (0, 0, dx dy). ∇×A 23 44 zb C1 G C2 _ za Figura 9: Igualdad de integrales al cambiar de arco: La curva C1 ∪ C2− es cerrada y la integral sobre ella se anula. La integrales sobre C1 o sobre C2 son iguales. Nota: Más generalmente, si C1 y C2 son dos arcos suaves a trozos que empiezan y acaban en los mismos puntos, C1 ∪C2− es una curva cerrada que, o bien es simple, o bien se puede descomponer en curvas cerradas simples. R Si f (z) esRanalı́tica en los interiores de esas curvas simples y continua en la frontera entonces C1 f (z) dz = C2 f (z) dz . Proposición. Sean C0 , C1 , . . . , Cn , n + 1 curvas suaves a trozos, simples, cerradas y con la misma orientación, tales que cada curva C1 , C2 , . . . , Cn está en el interior de C0 y en el exterior de las demás. Sea G el dominio formado por los puntos que son a la vez del interior de C0 y del exterior de C1 , C2 , . . . , Cn , y sea f (z) analı́tica en G y continua sobre su frontera C0 ∪ C1 ∪ · · · ∪ Cn .24 Entonces Z Z Z Z f (z) dz = f (z) dz + f (z) dz + · · · + f (z) dz . (5.20) C0 C1 C2 Cn Nota: La integral no tiene por qué ser 0 ya que no se exige que f (z) sea analı́tica en el interior de C1 , C2 , . . . , Cn . Z Demostración: Basta verlo para n = 2: Z Z Z f (z) dz − f (z) dz − f (z) dz = C0 C1 C2 f (z) dz + C0 Z C1− f (z) dz + Z C2− f (z) dz = 0 . (5.21) Por el teorema de la integral de Cauchy, ya que la integral sobre C0 ∪ C1− ∪ C2− se puede asimilar a la integral sobre un camino cerrado. (Véase la fig. 10.) ♦ 24 Esta construcción se ha considerado antes en la sección . Véase la figura 6. 45 _ C1 _ C2 C0 Figura 10: Igualdad de integrales sobre curvas cerradas: Si f (z) es analı́tica en la zona sombreada y al menos continua sobre las curvas, la integral sobre C0 ∪ C1− ∪ C2− se anula. El arco que une C0 con C1 se recorre primero en un sentido y luego en el otro y no contribuye a la integral, y lo mismo vale para el arco que une C0 con C2 . La integral sobre C0 es igual a la integral sobre C1 ∪ C2 . Ejemplo. Si f (z) es analı́tica fuera del conjunto cerrado E (véase la fig. 11) las integrales sobre C1 y C2 son iguales. Se puede ver notando que ambas coinciden con la integral sobre C. ⌢ Alternativamente, se ve notando que las integrales sobre los arcos za zb de la curvas C1 y C2 son ⌢ iguales, y lo mismo para los arcos zb za . Ejemplo. Sea C una Zcurva suave a trozos, cerrada, simple y orientada positivamente que no 1 pasa por z = 0. Calcúlese dz . C z Distinguimos dos casos: a) Que C no encierre z = 0 (es decir, que z = 0 no sea del interior de C). En este caso Z 1 dz = 0 (5.22) C z ya que f (z) = 1 es analı́tica en el interior de C y continua (de hecho analı́tica) sobre C. z b) Que C encierre el punto z = 0. Entonces existirá una circunferencia γR con centro 0 y radio R contenida en el interior de C. La función 1/z es analı́tica entre las dos curvas C y γR y sobre ellas, por tanto Z Z 1 1 dz = dz . (5.23) C z γR z 46 C1 G zb za E C C2 Figura 11: Igualdad de integrales sobre curvas cerradas: La integral sobre C1 , C2 y C son iguales si f (z) es analı́tica en G − E. Para z ∈ γR , z = R(cos θ + i sen θ), dz = R(− sen θ + i cos θ) dθ = iz dθ.25 Z 2π Z 1 dz = i dθ = 2πi . 0 C z Más generalmente (z0 ∈ 6 C) Z 1 0 si C no encierra z0 dz = ♦ 2πi si C encierra z0 y está orientada positivamente. C z − z0 (5.24) (5.25) 1 Ejemplo. Calcúlese la integral de f (z) = a lo largo del segmento recto que empieza en z = 1 z y acaba en z = i. f (z) es analı́tica en todo z excepto z = 0. Sea C1 el camino indicado, y sea C2 = {eiθ , 0 ≤ θ ≤ π/2}, que une los mismos puntos. (Véase la fig. 12.) Puesto que γ = C1 ∪ C2− es cerrado y no encierra a z = 0 la integral sobre γ se anula. Es decir, la integral sobre C1 es igual a la integral sobre C2 . Este es un arco de circunferencia de ángulo π/2 y radio 1, Z Z Z π/2 1 1 iπ dz = dz = i dθ = .♦ (5.26) 2 C1 z C2 z 0 25 O también d(Reiθ ) = iReiθ dθ = iz dθ cuando se defina ez y se demuestre la propiedad (ez )′ = ez en la Sec. . 47 i C2 C1 1 0 1 Figura 12: Caminos de integración equivalentes para f (z) = . z 5.4. Integrales complejas indefinidas Definición. Sea f (z) una función definida en un dominio G. Toda función (univaluada) F (z) tal que F ′ (z) = f (z) es una primitiva de f (z) en G. (Nótese que una primitiva siempre es analı́tica.) Teorema. Sea f (z) analı́tica en un dominio simplemente conexo G, entonces la integral Z z F (z) = f (ζ) dζ (5.27) z0 a lo largo de cualquier curva suave a trozos contenida en G, con punto inicial z0 (fijo) y final z (variable), define una primitiva de f (z) en G, es decir, una función univaluada y analı́tica en G con derivada F ′ (z) = f (z). Demostración: a) Veamos que F (z) no depende del camino y por tanto es univaluada: Si C1 y C2 son dos curvas que empiezan en z0 y acaban en z, C1 ∪C2− forma un camino cerrado. Como G es simplemente conexo, el interior I de C1 ∪ C2− está contenido en G y por tanto f (z) es analı́tica en I. En ese caso Z Z Z f (ζ) dζ = 0 y f (ζ) dζ = f (ζ) dζ , (5.28) C1 ∪C2− C1 y F (z) no depende del camino. 48 C2 b) Veamos que F ′ (z) = f (z): Sea z un punto cualquiera de G y sea z + h un punto de un entorno de z contenido en G Z z+h Z z Z z+h F (z + h) − F (z) = f (ζ) dζ − f (ζ) dζ = f (ζ) dζ , z, z + h ∈ G . (5.29) z0 z0 z La integral la tomamos sobre el segmento recto que va de z a z + h. Z 1 z+h F (z + h) − F (z) − f (z) = f (ζ) − f (z) dζ . h h z (5.30) Dado que f (z) es continua |f (ζ) − f (z)| < ǫ ∀ǫ > 0 tomando h suficientemente pequeño. Z F (z + h) − F (z) 1 z+h 1 − f (z) = ǫ|h| = ǫ . (5.31) f (ζ) − f (z) dζ < h |h| z |h| Se deduce que F (z + h) − F (z) = f (z) h→0 h F ′ (z) = lı́m (5.32) y F (z) es analı́tica en G. ♦ Teorema. Si Φ(z) es una primitiva de la función analı́tica f (z) en un dominio simplemente conexo G, entonces Z z Φ(z) = f (ζ) dζ + C z∈G (5.33) z0 donde z0 es un punto fijo arbitrario de G y C una constante compleja (constante respecto de z aunque dependerá de z0 ). Demostración: Definimos C(z) = Φ(z) − Z z f (ζ) dζ . (5.34) z0 Se trata de probar que C(z) es constante. Usando que la integral indefinida en un dominio simplemente conexo es una primitiva se sigue Z z d ′ ′ C (z) = Φ (z) − f (ζ) dζ = f (z) − f (z) = 0 . (5.35) dz z0 Sea C(z) = u(x, y) + iv(x, y), por las ecuaciones de Cauchy-Riemann 0 = C ′ (z) = ux + ivx = vy − iuy 49 (5.36) implica ux = vx = vy = uy = 0 y u, v, C son constantes en G. ♦ Se deduce que si Φ(z) es una primitiva de la función analı́tica f (z) en un dominio simplemente conexo G Z z1 f (ζ) dζ . (5.37) ∀z1 , z2 ∈ G Φ(z1 ) − Φ(z2 ) = z2 Lo que se ha visto es que en un dominio simplemente conexo una primitiva es una integral indefinida y viceversa. 5.5. Fórmula integral de Cauchy Teorema. (Fórmula integral de Cauchy.) Sea C una curva cerrada, simple y suave a trozos, y orientada positivamente, y sea f (z) analı́tica sobre C y en su interior, I.26 Entonces, Z f (z) 1 dz . (5.38) ∀z0 ∈ I , f (z0 ) = 2πi C z − z0 Demostración: Teniendo en cuenta que ∀z0 ∈ I , Z Z C C 1 dz = 2πi, la fórmula a probar equivale a z − z0 f (z) − f (z0 ) dz = 0 . z − z0 (5.39) Dado que f (z) es analı́tica, el integrando también es una función analı́tica en I − {z0 }. Por ello Z Z f (z) − f (z0 ) f (z) − f (z0 ) dz = dz , (5.40) z − z0 z − z0 C γR siendo γR una circunferencia de radio R y centro z0 contenida en I. Como f (z) es continua |f (z) − f (z0 )| < ǫ ∀ǫ > 0 eligiendo R suficientemente pequeño. Entonces, Z f (z) − f (z ) 0 < ǫ 2πR = 2πǫ → 0 , dz (5.41) R z − z0 γR lo cual demuestra el teorema. ♦ 26 Equivalentemente, C una curva suave a trozos, cerrada y simple, y orientada positivamente, f (z) es analı́tica en un dominio G que contiene a C y a su interior, I. 50 La fórmula integral de Cauchy demuestra que el valor de una función analı́tica en el interior de una curva cerrada está determinado por el valor de la función sobre la curva. Este resultado es muy notable. La afirmación análoga no es cierta por ejemplo para funciones reales diferenciables en R2 . Ejemplo. La función f : R2 → R 1 exp , x2 + y 2 < 1 f (x, y) = x2 + y 2 − 1 0, x2 + y 2 ≥ 1 (5.42) es diferenciable en todo R2 (de hecho infinitamente diferenciable), estrictamente positiva en el disco abierto x2 + y 2 < 1 e idénticamente 0 fuera de él. Luego fuera del disco x2 + y 2 < 1 la función es indistinguible de la función 0. ♦ Por ser f (z) = u(x, y) + iv(x, y) analı́tica, u, v satisfacen las ecuaciones de Cauchy-Riemann. El teorema dice que las condiciones de contorno consistentes en especificar u, v sobre C, son suficientes para resolver las ecuaciones en el interior de C, y (5.38) proporciona la solución en forma explı́cita. En realidad, como se verá en el capı́tulo , no hace falta conocer la función sobre toda la curva, sino que basta especificarla en un arco (abierto) de la curva, por pequeño que sea, para que la función quede completamente determinada. 5.6. Derivabilidad infinita de funciones analı́ticas Teorema. En las mismas condiciones del teorema de la fórmula integral de Cauchy, f (z) admite infinitas derivadas en I (el interior de la curva C), que vienen dadas por Z n! f (z) (n) f (z0 ) = dz , z0 ∈ I , n = 0, 1, 2, . . . (5.43) 2πi C (z − z0 )n+1 Demostración: La fórmula se demuestra por inducción notando que para n = 0 se recupera la fórmula integral de Cauchy. (No presentamos aquı́ la demostración detallada. Consúltese por ejemplo el libro de Silverman.) Intuitivamente el resultado se obtiene con facilidad a partir de la 51 d fórmula integral de Cauchy si conmuta con dz0 f (n) Z .27 En efecto, C Z dn 1 f (z) dn f (z0 ) = n dz (z0 ) = n dz0 dz0 2πi C z − z0 Z Z 1 n! dn f (z) f (z) = dz = dz . ♦ n 2πi C dz0 z − z0 2πi C (z − z0 )n+1 (5.44) Nota: Se ha obtenido el resultado notable de que si f (z) es derivable en un abierto G automáticamente tiene infinitas derivadas continuas en G, cosa que no ocurre para funciones reales. (Por ejemplo, f (x) definida como x2 para x > 0 y 0 para x ≤ 0 es derivable en todo R pero su derivada no lo es.) Si una función es analı́tica en G su derivada también es analı́tica (y por tanto también todas sus derivadas sucesivas). Z Teorema. (Teorema de Morera.) Sea f (z) continua en un dominio G y sea f (z) dz = 0 C para toda curva C cerrada y suave a trozos, contenida en G. Entonces f (z) es analı́tica en G. Demostración: La integral indefinida Z z F (z) = f (ζ) dζ , z0 z, z0 ∈ G (5.45) (integrando sobre un arco en G que una z0 con z) define una función univaluada ya que si C1 , C2 son dos arcos con punto inicial z0 y final z, la curva C1 ∪ C2− es cerrada y la integral sobre ella se anula por hipótesis. Usando que f (z) es continua (y siguiendo la demostración usada en el teorema de la pág. 48) se prueba que F (z) es derivable con F ′ (z) = f (z). De aquı́ se sigue que F (z) y f (z) son analı́ticas. ♦ 5.7. Índice de un camino cerrado Definición. Sea z0 ∈ C y C una curva suave a trozos cerrada que no pase por z0 . Se define el ı́ndice de C respecto de z0 mediante la fórmula Z 1 1 n(C, z0 ) = dz . (5.46) 2πi C z − z0 52 _1 1 1 2 1 0 Figura 13: Descomposición de C en dominios según el ı́ndice respecto de una curva cerrada. Ejemplo. Sea C la curva paramétrica z(t) = e−it , 0 ≤ t ≤ 4π (es decir, la circunferencia de radio 1 recorrida dos veces en sentido negativo). Y sea z0 = 0. Z Z 4π 1 1 1 dz 1 dt = (−i)e−it dt = −2 . ♦ (5.47) n(C, 0) = −it 2πi C z dt 2πi 0 e Propiedades. El ı́ndice es un número entero que cuenta el número de veces que C rodea z0 en sentido positivo. Por tanto, es invariante si se mueve z0 sin cruzar C o bajo una deformación continua de la curva C que no pase por z0 . Además el ı́ndice cambia de signo si se cambia la orientación de C. Ejemplo. Para la curva de la figura 13, indicamos los dominios de C con los distintos valores del ı́ndice asociado. Para obtener este resultado basta descomponer la curva en curvas simples. Alternativamente, para obtener n(C, z0 ) basta contar cuántas veces (con su signo) hay que cruzar C para llevar z0 al punto del infinito. Proposición. Si f (z) es analı́tica en un dominio simplemente conexo G, z0 ∈ G y C es una curva cerrada suave a trozos contenida en G y que no pasa por z0 , entonces Z f (z) 1 dz . (5.48) n(C, z0 )f (z0 ) = 2πi C z − z0 27 Esto se cumple ya que C es un conjunto compacto y f (z) es uniformemente continua en C y de hecho es infinitamente diferenciable con respecto a z0 para z ∈ C, z0 6∈ C. 53 f (z) z − z0 Demostración: Basta descomponer C en curvas simples y aplicar la fórmula integral de Cauchy a cada una. 5.8. Complementos Teorema. Si f (z) es analı́tica en un dominio G excepto en un conjunto de puntos aislados z1 , z2 , . . . ∈ G donde se sabe sólo que es continua, entonces es analı́tica en todo G. Demostración: Dado que los puntos son aislados basta demostrarlo para el caso de un único punto z1 y G simplemente conexo. La proposición se sigue del teorema de Morera una vez que se verifique que la integral de f (z) sobre cualquier curva cerrada y suave a trozos C, contenida en G, es cero. Si la curva no tiene a z1 en su interior la integral se anula por el teorema (generalizado) de la integral de Cauchy. Si z1 está en el interior de C, la integral no cambia si se reemplaza C por una circunferencia γǫ de radio ǫ > 0 centrada en z1 contenida en el interior de C. Esta integral tiende a 0 cuando ǫ → 0+ por ser f (z) continua en z = z1 . ♦ 54 Series complejas 6. 6.1. Convergencia y divergencia de series Definición. Una serie compleja es una suma infinita de números complejos ∞ X n=1 zn = z1 + z2 + z3 + · · · + zn + · · · , (6.1) donde zn es el término n-ésimo. La suma finita sn = z 1 + z 2 + z 3 + · · · + z n (6.2) se llama n-ésima suma parcial de la serie. ♦ Nota: Es importante enfatizar que cada serie está asociada unı́vocamente a la sucesión {zn } formada por sus términos. Dos sucesiones distintas (por ejemplo, reordenadas28 una respecto de otra) definen series distintas. Por otro lado, la información contenida en {zn } (sucesión de los términos) y en {sn } (sucesión de sumas parciales) es la misma ya que una sucesión se puede reconstruir a partir de la otra. P Definición. Una serie ∞ n=1 zn es convergente, sii lı́mn→∞ sn existe y es finito. Este lı́mite es la suma de la serie. En otro caso la serie es divergente. Si lı́mn→∞ sn = ∞ la serie es propiamente divergente, y si lı́mn→∞ sn no existe la serie es oscilante. P∞ P∞ z es convergente sii las series reales Teorema. Una serie compleja n n=1 Re (zn ) y n=1 P∞ Im (z ) son convergentes. n n=1 En consecuencia se pueden aplicar los criterios conocidos para el caso real. En particular, se deduce Teorema. Una condición necesaria de convergencia es que lı́mn→∞ zn = 0. ∞ X 1 Al igual que en el caso real esta condición no es suficiente, por ejemplo = ∞. n n=1 28 La reordenación puede consistir en aplicar permutaciones arbitrarias de términos (aplicación formal de la propiedad conmutativa) o permutaciones arbitrarias de paréntesis (aplicación formal de la propiedad asociativa). 55 6.2. Convergencia absoluta Definición. La serie P∞ n=1 zn es absolutamente convergente sii Esta condición es más exigente que la convergencia, de hecho: P∞ n=1 |zn | es convergente. Teorema. Si una serie es absolutamente convergente entonces es convergente. Demostración: Se demuestra como en el caso real. Definición. Una serie convergente que no es absolutamente convergente es condicionalmente convergente 1 1 1 Ejemplo. La serie 1 − + − + · · · es condicionalmente convergente, ya que converge 2 3 4 1 1 1 1 1 1 a log(2) pero 1 + + + + · · · diverge. La serie 1 − 2 + 2 − 2 + · · · es absolutamente 2 3 4 2 3 4 convergente. P P∞ ′ ′ Teorema. Si ∞ n=1 zn = s y n=1 zn = s y son dos series convergentes, ∞ X (αzn + α′ zn′ ) = αs + α′ s′ . (6.3) n=1 Demostración: Se demuestra como en el caso real. El producto de series requiere en general convergencia absoluta: P P∞ ′ Definición. Dadas dos series ∞ n=1 zn y n=1 zn , se define su producto en el sentido de Cauchy como la serie ′ z1 z1′ + (z1 z2′ + z2 z1′ ) + · · · + (z1 zn′ + z2 zn−1 + · · · + zn z1′ ) + · · · = z1′′ + z2′′ + · · · + zn′′ + · · · (6.4) P Es decir, la serie con término general zn′′ = nk=1 zk zn−k+1 . ♦ P P∞ ′ ′ Teorema. Si ∞ n=1 zn y n=1 zn son absolutamente P∞ ′′convergentes con sumas s y s , respectivamente, la serie producto en el sentido de Cauchy, zn , es a su vez absolutamente convergente, n=1 P P∞ ∞ ′ ′ con suma ss . Si cualquiera de las series z y n=1 n n=1 zn es condicionalmente convergente P∞ ′′ ′ n=1 zn puede ser divergente, pero si converge lo hace a ss . 56 P Nota: Si ∞ n=1 zn es absolutamente convergente su valor no cambia bajo reordenación arbitraria de la serie. La afirmación no es cierta para una serie condicionalmente convergente. De hecho, reordenando una serie real condicionalmente convergente se puede obtener cualquier valor prefijado, incluido infinito. 6.3. Convergencia uniforme Definición. Una serie de funciones es una serie cuyos términos son funciones, fn (z), definidas en un mismo dominio (de definición) E, ∞ X n=1 fn (z) = f1 (z) + f2 (z) + · · · + fn (z) + · · · . (6.5) Si la serie obtenida para cada valor de z ∈ E es convergente, la serie define una función s(z) que es su suma en E, ∞ X s(z) = fn (z) , ∀z ∈ E . (6.6) n=1 A la convergencia en cada punto se le denomina convergencia puntual de la serie de funciones. ♦ Obviamente s(z) es univaluada ya que las fn (z) lo son. En general s(z) no será continua en E aunque la funciones fn (z) lo sean. Ejemplo. 2 3 2 z + (z − z) + (z − z ) + · · · = 0 si |z| < 1 . 1 si z = 1 (6.7) Las sumas parciales son sn (z) = z n . La suma de esta serie de funciones no es continua en el intervalo real E = {0 ≤ z ≤ 1}, aunque fn (z) = z n − z n−1 es continua en E y la serie de funciones es convergente en E. ♦ P La continuidad de ∞ n=1 fn (z) = s(z) queda garantizada si se cumple una condición más fuerte: P Definición. Sea ∞ n=1 fn (z) = s(z) una serie de funciones convergente en E. La serie se dice que es uniformemente convergente sii ∀ǫ > 0 ∃ν(ǫ) tal que ∀n > ν y ∀z ∈ E |sn (z)−s(z)| < ǫ. (sn (z) es la n-ésima suma parcial.) Nota: La diferencia con la convergencia puntual es que en ésta ν(ǫ, z0 ) puede depender del 57 punto z0 y en la convergencia uniforme ν(ǫ) tiene que ser común para todos los puntos de E. Convergencia uniforme implica convergencia puntual. P n n−1 Ejemplo. z + ∞ ) no es uniformemente convergente en {|z| < 1} ya que |sn (z) − n=2 (z − z n s(z)| = |z | < ǫ no está garantizado simplemente tomando n suficientemente grande. Esto se debe a que lı́mz→1 |z|n = 1 y valores de z cada vez más próximos a |z| = 1 requieren n cada vez mayores. (Para cada n y ǫ no hay dificultad en elegir z, |z| < 1, suficientemente próximo a |z| = 1 de modo que |z n | ≥ ǫ.) En cambio esta serie de funciones sı́ es uniformemente convergente en la región {|z| ≤ R} para cualquier R, 0 < R < 1, ya que |z|n ≤ Rn → 0. n→∞ Lema. Si de E. P∞ n=1 fn (z) es uniformemente convergente en E también lo es en todo subconjunto Demostración: Es inmediato por la definición de uniformemente convergente. P∞ Lema. Si n=1 fn (z) es uniformemente convergente en E y g(z) es acotada en E, la serie P∞ g(z)f (z) también es uniformemente convergente en E. n n=1 Demostración: Si |g(z)| < K ∀z ∈ E, |sn (z) − s(z)| < ǫ implica |g(z)sn (z) − g(z)s(z)| < Kǫ que se puede hacer arbitrariamente pequeño tomando n suficientemente grande para todos los puntos de E a la vez. P Teorema. Si ∞ n=1 fn (z) converge uniformemente en un conjunto E y ∀n fn (z) es una función continua en E, entonces su suma s(z) es también una función continua en E. P Demostración: Por ser ∞ n=1 fn (z) uniformemente convergente, para cualquier ǫ > 0 hay un ν(ǫ) tal que |s(z0 ) − sn (z0 )| < ǫ y |s(z) − sn (z)| < ǫ , ∀n > ν (6.8) siendo z, z0 ∈ E cualesquiera. Además, por ser sn (z) continua en E, existe un δ(ǫ, n, z0 ) > 0 tal que |sn (z) − sn (z0 )| < ǫ siempre que |z − z0 | < δ . (6.9) Por la desigualdad triangular se deduce que |s(z) − s(z0 )| < 3ǫ siempre que |z − z0 | < δ y en consecuencia s(z) es continua en z0 . ♦ De la misma demostración se deduce que si las fn (z) son uniformemente continuas en E, la suma también. P Teorema. Si ∞ n=0 an es absolutamente convergente, y |fn (z)| ≤ |an | ∀n y ∀z ∈ E, entonces 58 P∞ n=1 fn (z) es uniforme y absolutamente convergente en E. Demostración: La convergencia absoluta es evidente ya que la serie de funciones P∞ está acotada término a término por una serie absolutamente convergente. Por otro lado, que n=0 an converja P∞ absolutamente implica que ∀ǫ > 0 ∃ν(ǫ) tal que n>ν |an | < ǫ. Entonces ∞ ∞ ∞ X X X |s(z) − sν (z)| = f (z) ≤ |f (z)| ≤ |an | < ǫ . (6.10) n>ν n n>ν n n>ν Puesto que ν(ǫ) es común a todos los puntos de E la convergencia es uniforme. ♦ P∞ Teorema. (Integración de series.) Sea C una curva suave a trozos, n=1 fn (z) una serie uniformemente convergente sobre C y fn (z) continua sobre C ∀n. Entonces, ! Z ∞ ∞ Z X X fn (z) dz = fn (z) dz . (6.11) C n=1 n=1 C R Demostración: La convergencia uniforme implica que ∀n > ν(ǫ) |s(z) − sn (z)| < ǫ, entonces | C (s(z) − sn (z)) dz| < ℓǫ → 0 (siendo ℓ la longitud de C). Se deduce n→∞ Z s(z) dz = lı́m n→∞ C Z sn (z) dz = lı́m C n→∞ n Z X k=1 fk (z) dz = C ∞ Z X n=1 C fn (z) dz . ♦ (6.12) P Teorema. (Teorema de Weierstrass.) Si ∞ n=1 fn (z) es una serie de funciones analı́ticas en un dominio G y uniformemente convergente en todo subconjunto compacto (cerrado y acotado) de G, entonces a) ∞ X fn (z) = s(z) es analı́tica en G . n=1 b) ∞ dk s(z) X dk fn (z) = en G, k = 1, 2, . . . k dz k dz n=1 Además la convergencia para las derivadas es uniforme en todo subconjunto compacto de G. Demostración: Para un punto z0 cualquiera de G, consideramos una circunferencia de radio R, γR , contenida en G y que encierre a z0 (no necesariamente centrada en z0 ). Cuando G no sea simplemente conexo elegimos R suficientemente pequeño de modo que el interior de γR esté contenido 59 en G y se pueda aplicar la fórmula integral de Cauchy. Fijada γR , a partir de ahora consideramos solamente puntos z0 contenidos en el interior de una circunferencia γr contenida en el interior de γR (r < R). Como s(z) es continua, por ser suma uniformemente convergente de funciones continuas, la siguiente integral existe: ∀z0 ∈ I(γr ) 1 2πi Z ∞ γR X 1 s(z) dz = z − z0 2πi n=1 ∞ Z γR X fn (z) dz = fn (z0 ) = s(z0 ) . z − z0 n=1 (6.13) En la primera igualdad conmutamos integral y el sumatorio por la convergencia uniforme. El lema que requiere que (z − z0 )−1 esté acotada (pág. 58) se aplica por r < R. Vemos que s(z0 ) satisface la fórmula integral de Cauchy para γR fijo y z0 variable. Esto directamente implica que s(z) es analı́tica en z0 , ya que la dependencia en z0 es analı́tica en la integral de la izquierda. Un cálculo explı́cito demuestra que la derivada en los z0 ∈ I(γr ) existe: Z s(z0 + ∆z0 ) − s(z0 ) 1 s(z) lı́m = − lı́m dz ∆z0 →0 ∆z0 →0 2πi γ (z − z0 − ∆z0 )(z − z0 ) ∆z0 R Z (6.14) s(z) 1 dz =− 2πi γR (z − z0 )2 Por otro lado k! s (z0 ) = 2πi (k) Z ∞ γR X k! s(z) dz = (z − z0 )k+1 2πi n=1 Z ∞ γR Se demuestra29 que esta convergencia es uniforme. ♦ 29 No se hace aquı́. Véase, por ejemplo el libro de Silverman 60 X fn (z) dz = fn(k) (z0 ) . (z − z0 )k+1 n=1 (6.15) Series de potencias 7. 7.1. Teorı́a básica Definición. Una serie de funciones de la forma ∞ X n=0 centrada en z = a.30 cn (z − a)n es una serie de potencias Estas series son de gran importancia en análisis complejo. A menudo se tomará a = 0 ya que todos los resultados se pueden generalizar fácilmente al caso a 6= 0. Definición. La región de convergencia de la serie de potencias es el conjunto de valores z para los que converge. (Como se verá, generalmente la región de convergencia es en efecto una región.) P n En algunos casos laP región es sólo z = 0, por ejemplo ∞ n=1 (nz) , y en otros es todo el plano ∞ n complejo, por ejemplo n=1 (z/n) . P n Lema. Si ∞ n=0 cn z converge en z1 6= 0, entonces es absolutamente convergente ∀z tal que |z| < |z1 |. Si diverge en z2 diverge ∀z tal que |z| > |z2 |. Demostración: Si ∞ X cn z1n es convergente entonces lı́mn→∞ cn z1n = 0 y se deduce n=0 ∃K > 0 tal que ∀n |cn z1n | < K . (7.1) Entonces, si |z| < |z1 | ∞ X ∞ ∞ X X n zn z n K cn z 1 < K = |cn z | = . n z1 z 1 − |z/z | 1 1 n=0 n=0 n=0 n (7.2) En el último paso se ha usado que |z/z1 | < 1 y en este caso la serie geométrica es convergente. La segunda parte del lema es consecuencia inmediata de la primera. ♦ Teorema. (Radio de convergencia.) Si la región de una serie de potencias no P∞de convergencia n es {z = 0} o C, existe un R > 0 (finito) tal que n=0 cn z converge absolutamente si |z| < R y diverge si |z| > R. 30 Se entiende c0 + P∞ n=1 cn (z − a)n , de modo que en z = a queda c0 . Es decir, z 0 = 1 ∀z incluido z = 0. 61 Demostración: Sea G̃ la región de convergencia. Por hipótesis, {0} ( G̃ ( C, es decir, hay puntos z1 6= 0 en G̃ y puntos z2 en C − G̃. Del lema se sigue que 0 < |z1 | ≤ |z2 | < ∞. R es el supremo de los |z1 | y el ı́nfimo de los |z2 | y 0 < R < ∞. También por el lema, la convergencia en |z| < R es absoluta. ♦ Definición. Se deduce que cuando G̃ 6= {0} la región de convergencia es en efecto una región, ya que es C o el disco abierto de radio R junto con parte de su frontera (a saber, los posibles puntos de convergencia con |z| = R). A R se le denomina radio de convergencia, 0 ≤ R ≤ ∞ (0 o ∞ si la región de convergencia es {0} o C, respectivamente). P n Teorema. Si ∞ n=0 cn z tiene radio de convergencia R no nulo, la convergencia es uniforme en cualquier subconjunto compacto de {|z| < R}. Demostración: Todo subconjunto compacto E del disco abierto {|z| < R} está contenido en algún disco cerrado D̄r = {|z| ≤ r} con r < R. (En efecto, ya que necesariamente habrá una distancia mı́nima no nula entre los puntos de E y la circunferencia |z| = R, por ser E compacto.) Por el lema de pág. 58 basta demostrar la convergencia uniforme en D̄r . P n Para |z| ≤ r < R, |cn z n | ≤ |cn P |rn y la serie ∞ n=0 cn r es absolutamente convergente por n r < R. Por el teorema en la pág. 59, ∞ n=0 cn z converge uniformemente en D̄r . ♦ P n Teorema. Dada una serie con radio de convergencia R > 0, su suma s(z) = ∞ n=0 cn z es analı́tica en |z| < R, además ∞ X ′ s (z) = ncn z n−1 , (7.3) n=1 y esta serie tiene el mismo radio de convergencia. Demostración: En efecto, aplicando el teorema de Weierstrass al dominio G = {|z| < R}, se sigue que la suma s(z) es analı́tica en G y que la derivada conmuta con la suma infinita. Dado que la serie de las derivadas converge en G se deduce que R′ ≥ R (siendo R y R′ los dos radios de convergencia). Por otro lado |ncn z n−1 | ≥ 1 |cn z n |, |z| (n ≥ 1) (7.4) implica que cuando la serie de las derivadas converge la original también, R′ ≤ R. De aquı́ se sigue R′ = R. ♦ 62 7.2. Determinación del radio de convergencia Los criterios de convergencia de series reales se pueden aplicar para determinar el radio de convergencia. ∞ X an Ejemplo. Según el criterio del cociente, si existe el lı́mite lı́m = α, la serie an n→∞ an−1 n=0 converge absolutamente si α < 1 y diverge si α > 1. Para la serie an = cn z n , hay convergencia cn sea menor o mayor que 1, respectivamente. absoluta o divergencia siempre que α = |z| lı́m n→∞ cn−1 Es decir, cn 1 = lı́m (7.5) R n→∞ cn−1 si el lı́mite existe. ♦ Ejemplo. Para P∞ n=0 z n /n!, cn /cn−1 = 1/n → 0, y R = ∞. n→∞ Un criterio especialmente útil en este contexto es el criterio de Cauchy de convergencia de una ∞ X 1/n serie: Sea lı́m |an | = α, la serie an converge absolutamente si α < 1 y diverge si α > 1. n→∞ n=0 Aplicando este criterio a an = cn z n , se deduce que cuando existe lı́m |cn |1/n = l el radio de la serie n→∞ viene dado por R = 1/l. Definición. Sea a1 , a2 , . . . , an , . . . una sucesión de números reales no negativos. Se define el lı́mite superior de {an }, que se denota lı́m an , como el mayor de los puntos lı́mite de {an }, o n→∞ bien +∞ si la sucesión es no acotada superiormente. El lı́mite superior coincide con el lı́mite usual cuando este último existe. El lı́mite superior siempre existe y es no negativo. P n Teorema. (Criterio de Cauchy-Hadamard.) Sea la serie de potencias ∞ n=0 cn z , y sea l = lı́m |cn |1/n , n→∞ 1 entonces el radio de convergencia es R = , con 0 ≤ l ≤ +∞. l Demostración: 63 (7.6) a) Caso l = +∞. Entonces {|cn |1/n } es no acotada. Esto implica: |cn |1/n > K ∀K > 0 para infinitos valores de n . (7.7) 1 y se deduce |cn z n | > 1 para |z| infinitos valores de n. Por tanto la serie no converge si z 6= 0 y se sigue que R = 0. En particular, para cualquier z 6= 0 se puede tomar K = b) Caso l = 0. Entonces {|cn |1/n } es acotada y no negativa y al ser l = 0 el mayor punto lı́mite debe ser también el lı́mite, lı́mn→∞ |cn |1/n = 0. Es decir, ∀ǫ > 0 ∃ν(ǫ) tal que ∀n > ν |cn |1/n < ǫ . (7.8) 1 1 y se sigue que |cn z n | < n 2|z| 2 ∀n > ν. Por tanto la región de convergencia es C y R = ∞. En este caso, para cualquier z 6= 0, se puede tomar ǫ = c) Caso l finito y no nulo. Entonces, ∀ǫ > 0 ∃ν(ǫ) tal que ∀n > ν |cn |1/n < l + ǫ .31 (7.9) 1 En este caso, sea z1 cualquiera tal que |z1 | < . Tomando l 1 − l|z1 | ǫ= > 0, 2|z1 | |cn | 1/n 1 + l|z1 | < , 2|z1 | |cn z1n | < 1 + l|z1 | 2 n = rn , (7.10) y la serie converge en z1 por r < 1. Análogamente, por ser l un punto lı́mite ∀ǫ > 0 |cn |1/n > l − ǫ para infinitos valores de n. (7.11) 1 En este caso, sea z2 cualquiera tal que |z2 | > . Tomando l ǫ= l|z2 | − 1 > 0, |z2 | |cn |1/n > 1 , |z2 | |cn z2n | > 1 , (7.12) 1 y la serie diverge en z2 . En consecuencia R = . ♦ l 31 En otro caso, habrı́a infinitos términos por encima de l + a para cierto a > 0 y al estar la serie acotada (por l finito) habrı́a otro punto lı́mite mayor que l. 64 Ejemplo. a) 1 + z + z 4 + z 9 + · · · . Los puntos lı́mite de {|cn |1/n } son 0 y 1. En consecuencia l = 1 y R = 1. b) 1 + ∞ X zn n=1 c) ∞ X n=0 d) , s ≥ 0 . En este caso l = lı́m n−s/n = lı́m e−s log n/n = e0 = 1. Por tanto R = 1 . n→∞ n→∞ n!z n . En este caso l = ∞ y R = 0 ya que n! > rn ∀r > 0 y ∀n > ν(r). ∞ X zn n=0 ns n! . Es inmediato que l = 0 y R = ∞. ♦ La convergencia de una serie de potencias en los puntos tales que |z| = R depende del caso. Ejemplo. Para la serie 1 + ∞ X zn n=1 ns : a) 1 + z + z 2 + z 3 + · · · (s = 0), diverge ∀z, |z| = 1. 1 1 b) 1 + z + z 2 + z 3 + · · · (s = 1), converge ∀z 6= 1, |z| = 1. 2 3 c) 1 + z + 1 1 2 z + 2 z 3 + · · · (s = 2), converge ∀z, |z| = 1. ♦ 2 2 3 65 Exponencial y funciones relacionadas 8. Exponencial, coseno y seno 8.1. Definición. Una función compleja f (z) es entera si es analı́tica en todo el plano complejo finito. Ejemplo. Un polinomio en z, P (z) = a0 + a1 z + · · · + an z n , es una función entera. ∞ X 1 n z converge ∀z ∈ C y por tanto es entera. Para z = x ∈ R Como vimos la función n! n=0 coincide con ex , por ello definimos: Definición. ∞ X 1 n z2 z3 a) e := z =1+z+ + + ··· . n! 2! 3! n=0 z b) cos(z) := 1 − z2 z4 z 2k + + · · · + (−1)k + ··· . 2! 4! (2k)! c) sen(z) := z − z 2k+1 z3 z5 + + · · · + (−1)k + ··· . 3! 5! (2k + 1)! cos(z) y sen(z) coinciden con cos(x) y sen(x) cuando z = x ∈ R y también son funciones enteras. ez también se denota exp(z). ♦ Proposición. La fórmula ez1 ez2 = ez1 +z2 ∀z1 , z2 ∈ C válida para z1 , z2 reales también es válida en el caso complejo. 66 (8.1) Demostración: En efecto, z1 z2 e e ∞ ∞ ∞ ∞ X 1 nX 1 m XX 1 n+m n m z1 z2 z z = = n n! 1 m=0 m! 2 (n + m)! n=0 m=0 n=0 ∞ ∞ N X X 1 X N 1 n N −n = (z1 + z2 )N = ez1 +z2 , z1 z2 = n N ! n=0 N! N =0 N =0 (8.2) donde se ha utilizado la convergencia absoluta de las series para reordenar las series. ♦ Propiedades: e z1 = ez1 −z2 . e z2 a) Dado que e0 = 1, se deduce e−z = (ez )−1 y b) La convergencia absoluta de la serie en C permite reordenar las series: z2 z4 z3 z5 (iz)2 (iz)3 iz + + ··· = 1 − + + ··· + i z − + + ··· e = 1 + iz + 2! 3! 2! 4! 3! 5! = cos z + i sen z (Fórmula de Euler) (8.3) c) Además, como se obtiene directamente de sus series, sen(−z) = − sen(z). cos(−z) = cos(z), Se deduce e−iz = cos z − i sen z, y por tanto 1 iz e + e−iz , cos z = 2 d) ez es periódica con periodo 2πi, es decir, sen z = 1 iz e − e−iz . 2i ez = ez+2πi . ∀z ∈ C (8.4) (8.5) (8.6) En efecto, ez+2πi = ez e2πi = ez (cos(2π) + i sen(2π)) = ez . Iterando la fórmula se obtiene ∀z ∈ C ∀n ∈ Z ez = ez+2πin . (8.7) e) Como sabemos, ∀z ∈ C hay una forma polar: z = r(cos θ + i sen θ), donde r ≥ 0, 0 ≤ θ < 2π. Se deduce z = reiθ , que es la forma exponencial de z. También se obtiene la relación ez = ex+iy = ex eiy = ex (cos y + i sen y) , (8.8) que proporciona una definición alternativa de exp z y la reduce a funciones reales conocidas. 67 f ) ez no se anula para ningún valor de z. En efecto, |ez | = ex+iy = ex eiy = |ex | eiy = ex > 0 ∀x, (8.9) implica ∀z ez 6= 0. El mismo resultado se deduce la existencia de (ez )−1 a saber, e−z g) Las fórmulas de adición y sustracción trigonométricas se aplican igualmente al caso complejo: ∀z1 , z2 ∈ C cos(z1 ± z2 ) = cos z1 cos z2 ∓ sen z1 sen z2 , sen(z1 ± z2 ) = sen z1 cos z2 ± cos z1 sen z2 . (8.10) Se deduce de la fórmula de Euler. Por ejemplo, eiz1 − e−iz1 eiz2 − e−iz2 eiz1 + e−iz1 eiz2 + e−iz2 − 2 2 2i 2i ei(z1 +z2 ) + e−i(z1 +z2 ) = cos(z1 + z2 ). (8.11) = 2 cos z1 cos z2 − sen z1 sen z2 = Además, tomando z1 = z, z2 = 2π, se sigue que cos z y sen z son funciones periódicas: ∀z ∈ C cos(z + 2π) = cos z , sen(z + 2π) = sen z . (8.12) Por otro lado, tomando z1 = −z2 = z ∀z ∈ C cos2 z + sen2 z = 1 . (8.13) Sin embargo, | cos z| y | sen z| no están acotados por 1 fuera del eje real. Finalmente, tomando π z1 = , z2 = −z, 2 π (8.14) ∀z ∈ C cos z = sen( − z) . 2 h) Soluciones de ez = 1: ez = 1 sii z = 2πin ∀n ∈ Z . (8.15) En efecto, 1 = |ez | = ex implica x = 0, entonces 1 = cos y+i sen y implica y = 2πn, n ∈ Z . i) Ceros de cos z y sen z en C: 0 = sen z = 0 = sen z 1 iz (e − e−iz ) implica e2iz = 1 . Se deduce 2i sii z = πn ∀n ∈ Z . (8.16) Usando cos z = sen( π2 − z) se obtiene 0 = cos z 1 sii z = π n + 2 68 ∀n ∈ Z . (8.17) 8.2. Funciones hiperbólicas Definición. Extendiendo la definición de z real a complejo, se define 1 cosh z = (ez + e−z ) , 2 1 senh z = (ez − e−z ) . 2 (8.18) Estas funciones son enteras con desarrollo en serie absolutamente convergente en todo C: cosh z = ∞ X z 2n , (2n)! n=0 senh z = ∞ X n=0 z 2n+1 . (2n + 1)! (8.19) Se deduce cosh z = cos(iz) , cos z = cosh(iz) , senh z = −i sen(iz) , sen z = −i senh(iz) . (8.20) La funciones cosh z y senh z no están acotadas en R y por tanto tampoco en C. La funciones hiperbólicas en C satisfacen cosh2 z − senh2 z cosh(z1 ± z2 ) senh(z1 ± z2 ) cosh z 8.3. = = = = 1, cosh z1 cosh z2 ± senh z1 senh z2 , senh z1 cosh z2 ± cosh z1 senh z2 . cosh(z + 2πi) , senh z = senh(z + 2πi) . (8.21) Derivadas de exp, cos, sen, cosh, senh Basta usar la propiedad de derivación de una serie término a término. Dado que las series son las mismas que en el caso real se obtienen las mismas relaciones dez = ez , dz d sen z d cos z = − sen z , = cos z , dz dz d senh z d cosh z = senh z , = cosh z . dz dz 69 (8.22) 8.4. Función logaritmo En el caso real, el logaritmo32 se define como la función inversa de la exponencial, es decir, si x > 0 y x = ey , log x = y. y es la única solución de x = ey . Si x ≤ 0 no hay solución. El logaritmo complejo se introduce de manera análoga. Definición. La función inversa de z = ew se llama logaritmo (neperiano), w = log z. w es cualquiera de las soluciones de z = ew . Propiedades: a) z = 0 no tiene logaritmo. Como vimos ew = 0 no tiene solución en el plano complejo finito. b) log z es una función multivaluada, ya que si w es una solución, cualquier otro número de la forma w + 2πin, (n ∈ Z) también es solución. En efecto, como vimos la exponencial es una función periódica y ew+2πin = ew . Por tanto la multivaluación del logaritmo complejo es infinita (a diferencia de z 1/n que toma |n| valores). Por otro lado, ésta es la única multivaluación: Si w1 , w2 son dos logaritmos de z, entonces w2 = w1 + 2πin para algún entero n. En efecto, ∀z 6= 0 z = e w1 =e w2 , e w2 1 = w1 = ew2 −w1 e implica w2 − w1 = 2πin, n ∈ Z. (8.23) c) Si w = u + iv, (u, v ∈ R) la ecuación z = ew = eu+iv = eu eiv implica |z| = |eu ||eiv | = eu , es decir log |z| = u, y entonces arg z = v, de donde33 w = log z = log |z| + i arg z . (8.24) arg z es una función multivaluada y lo mismo log z. Si se elige la determinación principal del argumento, Arg z ∈ [0, 2π[, se obtiene la determinación principal del logaritmo Log z = log |z| + i Arg z . (8.25) En general, log z = log |z| + i Arg z + 2πik , 32 k ∈ Z. (8.26) Designamos el logaritmo neperiano por log en vez de ln ya que no hay posibilidad de confusión con el logaritmo decimal, que no se va a usar aquı́. 33 Hay una ambigüedad en la notación, ya que log |z| se refiere al logaritmo real (univaluado), es decir, el definido en R+ → R. Cuando x > 0 se sobreentiende que log x es el logaritmo real. 70 Ejemplo. Log 1 = 0, Log ( − 1) = iπ, 3πi , Log ( − i) = 2 Log (2i) = log 2 + log 1 = 2πin, n ∈ Z log(−1) = (2n + 1)iπ, n ∈ Z iπ , 2 Log (1 + i) = 1 iπ log 2 + . 2 4 (8.27) d) La función Log z está definida en C − {0} pero es discontinua a lo largo del semieje real positivo, R+ := {x ≥ 0}. En efecto, Arg z vale casi 0 si z está casi en R+ − {0} pero en el semiplano superior ( Im z > 0) y 2π si z está casi en R+ − {0} pero en el semiplano inferior Im z < 0: ∀a > 0 , lı́m Log z = log a , z→a Im z>0 lı́m Log z = log a + 2πi . z→a (8.28) Im z<0 (De hecho Log a = log a.) Lo mismo se puede expresar mediante (para a > 0) lı́m Log (a − iǫ) = log a + 2πi . lı́m Log (a + iǫ) = log a , ǫ→0 ǫ→0 (8.29) ǫ>0 ǫ>0 A veces la notación se simplifica y se escribe simplemente Log (a + iǫ) = log a, Log (a − iǫ) = log a + 2πi (se sobreentiende que ǫ → 0 desde ǫ > 0.) También se usa la notación Log (a + i0+ ) = log a, Log (a − i0+ ) = Log (a + i0− ) = log a + 2πi. Más generalmente f (0+ ) = lı́m f (ǫ) . ǫ→0 ǫ>0 (8.30) e) Por construcción exp(log z) = z. En cambio, en general, Log ( exp w) no coincidirá con w. (Por ejemplo, Log (e−iπ ) = iπ.) w será uno de los logaritmos log(exp w). La relación ew1 +w2 = ew1 ew2 implica que log(z1 z2 ) = log(z1 ) + log(z2 ) ( mód 2πi) (8.31) Log (z1 z2 ) = Log (z1 ) + Log (z2 ) + 2πin(z1 , z2 ) (8.32) o también donde n(z1 , z2 ) = Análogamente 0, 0 ≤ Arg z 1 + Arg z 2 < 2π . −1 , 2π ≤ Arg z 1 + Arg z 2 < 4π log(z n ) = n log(z) ( mód 2πi) 71 n ∈ Z. (8.33) log z = log z + 4 π i 2 0 w log z = log z + 2 π i 1 0 log z 0 w w0 z z 0 z Figura 14: Representación esquemática de las varias ramas w = log z. La derivada es común a w − w0 eligiendo para z0 y z la misma rama de todas las ramas y se puede calcular como lı́m z→z0 z − z0 log z por continuidad. f ) La función Log z es discontinua sobre el semieje real positivo, {x ≥ 0}. Fuera de esos puntos la función es analı́tica y su derivada se obtiene a partir de la de la exponencial mediante la regla de la cadena, como en el caso real.34 Equivalentemente, d Log z dw 1 1 1 = w = w = w = , de dz de e z dw z 6∈ {x ≥ 0} . (8.34) 1 es regular en todo C excepto 0, incluido el semieje real positivo. Más generalz mente, cualquiera que sea la elección de arg z (por ejemplo arg z ∈] − π, π]) si se elige de forma continua en un entorno de z que excluya 0, permite calcular la derivada y se obtiene el mismo resultado 1/z: En efecto, las distintas elecciones difieren en un término aditivo 2πin que es constante y no afecta a la derivada (véase la fig. 14) La función 1 d log z = . dz z 34 Es decir, z = elog z , 1= delog z d log z dz d log z = = elog z =z , dz dz dz dz 72 (8.35) d log z 1 = . dz z Sólo en z = 0, ∞ la función logaritmo es intrı́nsecamente no analı́tica (es decir, no analı́tica bajo ninguna elección de arg z.) 8.5. Función potencia general Usando el logaritmo se puede construir la función potencia general, w = z a donde z y a son ambos complejos, z 6= 0, mediante z a := exp(a log z) , a, z ∈ C z 6= 0 . (8.36) Es decir, si z = reiθ , z a = ea log r eiaθ , siendo θ cualquiera de los argumentos de z. En general esta función tiene multivaluación infinita, heredada del logaritmo. La determinación principal es (z a )p := exp(a Log z) , a, z ∈ C z 6= 0 . (8.37) y todos los demás valores son de la forma z a = (z a )p e2πian , n ∈ Z. (8.38) La multivaluación es finita sii a es un número racional (real). En efecto, el factor e2πian debe tomar sólo un número finito de valores distintos, y por tanto debe haber valores distintos de n que den el mismo valor para e2πian . Si n1 y n2 son dos tales valores e2πian1 = e2πian2 implica a(n1 − n2 ) = k ∈ Z y a = k/(n1 − n2 ) es racional. Por otro lado, si a = p/q, siendo q, p enteros primos entre sı́ y q positivo, para cualquier n entero n = kq+r, 0 ≤ r < q con k y r únicos. Entonces ′ e2πian = e2πipk e2πipr/q = e2πipr/q , y se producen q valores distintos. En efecto, e2πipr/q = e2πipr /q sii pr/q − pr′ /q = m ∈ Z, entonces p(r − r′ ) = qm, dado que p no es múltiplo de q, lo debe ser r − r′ y ya que 0 ≤ r, r′ < q se deduce r = r′ . Por otro lado z a+b toma un conjunto de valores que es un subconjunto de los valores que√puede √ a b a+b 0 a b tomar z z . (Por ejemplo, para a = −b = 1/2, z = z = 1, en cambio z z = (± z)(±1/ z) = ab a b ±1.) Del mismo modo, z es un subconjunto de (z ) . (Por ejemplo, para a = 2 y b = 1/2, z ab = z, √ en cambio (z a )b = ± z 2 = ±z.) Casos particulares: Si a = n ∈ Z z a |a=n = en log z = elog(z 73 n )+2πik = zn . (8.39) Análogamente, cuando a = z a |a= 1 n 1 , (n ∈ Z − {0}) n 1 1 log z = exp (log |z| + i arg z) = exp n n = |z|1/n e(i arg z)/n = z 1/n (|n| valores distintos). (8.40) Éstas son las |n| soluciones de wn = z. La derivada también es una función multivaluada (z a )′ = ea log z 8.6. a = az a−1 . z (8.41) Funciones trigonométricas inversas Las funciones trigonométricas e hiperbólicas inversas se pueden expresar mediante el logaritmo. Por ejemplo, la función w = cos−1 z (o arc cos z) se define como cualquier solución de la ecuación cos w = z. Esto produce z = cos w = eiw + e−iw , y 0 = (eiw )2 − 2z eiw + 1 . 2 Esta es una ecuación de segundo grado que puede resolverse en eiw y por tanto en w, √ cos−1 z = w = −i log(z + z 2 − 1). √ Nótese que tanto log z como z son funciones multivaluadas. Análogamente 1 + iz 1 −1 , log tan z = 2i 1 − iz √ senh−1 z = log z + z 2 + 1 , √ −1 2 sen z = −i log iz + 1 − z . 74 (8.42) (8.43) (8.44) 9. 9.1. Funciones multivaluadas Dominios de univalencia Definición. Una función (univaluada) w = f (z) es univalente en un dominio G si es analı́tica e inyectiva.35 En este caso se dice que G es un dominio de univalencia de f (z). Usando el teorema de Rouché (ver página 143) es posible demostrar que en este caso f ′ (z) 6= 0 ∀z ∈ G. (Consúltese por ejemplo el libro de Silverman.) Se deduce entonces que la función inversa, z = ϕ(w), también es derivable. En efecto:36 dz 1 1 dϕ(w) = = . (9.1) = ′ dw dw dw f (z(w)) dz G E A +z A f Γ z + B w + γ + ϕ w Figura 15: Si z, z ′ están conectados por el arco Γ ⊂ G, sus imágenes w, w′ lo estarán por la imagen de Γ, γ ⊂ E. Por ser ϕ continua, todo entorno suficientemente pequeño B de w es la imagen de un entorno de z, A′ ⊂ G y por tanto B ⊂ E. Teorema. Sea w = f (z) univalente en un dominio G y sea E el recorrido asociado a G. Entonces E también es un dominio (en el plano w) y ϕ(w) es univalente en E. 35 O equivalentemente, biyectiva, considerando f como una aplicación de G en su recorrido E. Suponiendo que la derivada exista, se puede también calcular usando la regla de la cadena: derivando w = f (z) = f (ϕ(w)) respecto de w resulta 1 = f ′ (ϕ(w))ϕ′ (w). 36 75 Demostración: Hay que probar que E = {w w = f (z), z ∈ G} es abierto y conexo. (Véase fig. 15.) ⌢ 1. E es conexo: Si w1 = f (z1 ) y w2 = f (z2 ) la imagen del arco z1 z2 ⊂ G es también un arco (curva continua por f (z) continua) contenida en E. 2. E es abierto: Sea w un punto cualquiera de E y z = ϕ(w). Dado que ϕ(w) es continua (por ser derivable), para todo entorno de z, A ⊂ G, hay un entorno B de w tal que la imagen de B por ϕ, A′ , está contenida en A y por tanto en G, esto implica B ⊂ E y w es un punto interior. Puesto que E es un dominio y ϕ(z) es invertible y derivable en cada punto de E, ϕ(z) es univalente en E. ♦ 9.1.1. Potencia y raı́z n-ésima Sea w = z n , n entero positivo. Dado cualquier w 6= 0, w = reiθ (r > 0) hay n valores z tales que z n = w, a saber z = r1/n ei(θ+2πk) , k = 0, 1, . . . , n − 1. El conjunto {w1/n } forma un polı́gono regular de n lados en el plano z. Es evidente que si se restringe arg z al intervalo 2π (c real) (9.2) c < arg z < c + n entonces z1 6= z2 implica z1n 6= z2n , y la función z n es inyectiva. Se deduce que z n es univalente en 2π }. Además G es maximal, es decir, no existe un G′ ) G tal G = {z z 6= 0, c < arg z < c + n que z n sea univalente. En particular, para c = 0, G = {z z 6= 0, 0 < arg z < 2π/n} y su imagen es E = {w w 6= 0, 0 < arg w < 2π}. Este conjunto es C − {u ≥ 0} y se denomina plano complejo cortado según el semieje real positivo.37 (Véase fig. 16.) 2π En un dominio de univalencia, por ejemplo, G = {z z 6= 0, 0 < arg z < }, la función w = z n n tiene una inversa, z = w1/n . Esta inversa es univalente en E = {w w 6= 0, 0 < arg w < 2π}, con derivada n −1 1 dw1/n 1 dz = n−1 = w−1+1/n . = (9.3) dw dz nz n 37 Como es usual, denotamos u = Re w, v = Im w, x = Re z e y = Im z. 76 z1 y v w=z 6 G E z0 z2 x u z5 z 3 z4 plano z plano w Figura 16: La zona sombreada en el plano z (la frontera no está incluida) es un dominio de univalencia maximal para w = z 6 , G = {z 6= 0, 0 < arg z < 2π/6} . La zona sombreada en el plano w (sin incluir la frontera) es el recorrido, E = {w 6= 0, 0 < arg w < 2π}. Es todo el plano complejo excepto los número reales no negativos. 9.1.2. Exponencial y logaritmo Sea w = ez . Esta función no es biyectiva en C. En efecto, e z1 = e z2 sii z2 = z1 + 2πik k = 0, ±1, ±2, . . . (9.4) Para que w = ez sea una biyección basta restringir Im z. El dominio G = {z c < Im z < c+2π} z es un dominio de univalencia maximal de w = e y el recorrido es E = {w w 6= 0 , c < arg w < c + 2π}. (Véase la fig. 17.) La función inversa es el logaritmo z = log w. Esta función es univalente en E. En el caso particular de c = 0, G = {z 0 < Im z < 2π}, el recorrido es el plano complejo cortado según el semieje real positivo, E = {w w 6= 0 , 0 < arg w < 2π} y corresponde a la determinación principal del argumento de w, Arg w ∈ [0, 2π[, y a la determinación principal del logaritmo, Log w (excepto que arg w = 0 está excluido del dominio). 77 y 2 πi w=e z v E G x 0 u plano z plano w Figura 17: G = {0 < Im z < 2π} es un dominio de univalencia maximal de w = ez . El recorrido E es el plano complejo w excepto los números reales no negativos. 9.2. Ramas y puntos de ramificación 2(n − 1)π 2π 4π , ,... , se obtienen n dominios de univalencia Gk : n n n 2πk 2π(k + 1) , k = 0, 1, 2, . . . , n − 1 . (9.5) 6 0, < arg z < Gk = z z = n n Si en w = z n tomamos c = 0, n−1 Estos dominios son disjuntos y su unión, junto con sus fronteras, es C, ∪k=0 Ḡk = C. Además el recorrido E = {w 6= 0, 0 < arg w < 2π} = C − {u ≥ 0} es común a todos ellos (por 2πk < arg w = n arg z < 2π(k + 1)). (Véase la fig. 18.) Como w = z n es univalente en cada Gk , se obtiene una función inversa para cada k, ϕk : E → Gk , que denotamos z = (w1/n )k . La función multivaluada w1/n (que hace corresponder a cada w el conjunto de soluciones de w = z n ) está definida en todo C∗ . Cada una de las funciones z = (w1/n )k , k = 0, . . . , n − 1, se llama rama de la función multivaluada w1/n . La frontera del dominio de definición de cada rama se denomina corte de rama. En este caso el corte de rama es el semieje real positivo, {u ≥ 0}. Análogamente, para la función w = ez , se puede definir un conjunto de dominios o n Gk = z 2πk < Im z < 2π(k + 1) , k ∈ Z . 78 (9.6) y w=z 6 v E G1 G G2 0 x G3 u G5 G 4 plano z plano w Figura 18: C se descompone en 6 dominios de univalencia maximales (junto con sus fronteras) de la función w = z 6 . Todos ellos tienen el mismo recorrido E. Cada uno de estos dominios define una rama de la función. con recorrido común E = C − {u ≥ 0}, y tal que la unión de todos los dominios junto con sus fronteras recubren el plano complejo, ∪k∈Z Ḡk = C. Esto define una función inversa para cada k, z = (log w)k , w ∈ E, z ∈ Gk , todas ellas univalentes en E. (Véase la fig. 19.) La función multivaluada log w está definida como la inversa de ez . Cada función (log w)k es una rama de la función multivaluada log w y el semieje real positivo es el corte de rama. Es importante notar que la descomposición de las funciones multivaluadas en ramas depende de la elección de dominios de univalencia en los que se descompone C, y esta elección, denominada ramificación de la función multivaluada, no es única. Por ejemplo, si para w = z n se toman los dominios de univalencia Dk = {z z 6= 0, (2k −1)π/n < arg z < (2k +1)π/n}, k = 0, 1, . . . , n−1, entonces el recorrido común a estos dominios es E ′ = {w w 6= 0, − π < arg w < π} (plano complejo cortado según el semieje real negativo). (Véase la fig. 20.) Es decir, se obtiene otra forma válida de cubrir el plano z y otro conjunto de ramas de w1/n . En este caso el corte de rama es el semieje real negativo {u ≤ 0}. Más generalmente, puede tomarse como corte de rama cualquier arco simple C, que una 0 con ∞. E ′′ = C − C define un dominio maximal de univalencia para w1/n y n ramas de esta función. (Igualmente esta construcción define un conjunto de ramas para log w. Véase la fig. 21.) Se ve pues que el corte de rama concreto (puntos donde la función no está definida) no es intrı́nseco a la función multivaluada w1/n mientras que sı́ lo son w = 0 y w = ∞. En estos puntos w1/n no es 79 y G1 w=e 2πi z v E G0 0 x 2πi u G−1 plano z plano w Figura 19: Descomposición del plano z en dominios de univalencia maximales para la función w = ez y recorrido en el plano w. analı́tica independientemente de como se elija la ramificación. Para ver esto con más detalle, consideremos una curva Γ en el plano w (de la función w = z n ) cerrada, simple y orientada positivamente, con punto inicial y final w0 y que no pase por w = 0. 1/n Tomemos z0 = (w0 )k para cierto k, es decir, z0 es una de las raı́ces n-ésimas de w. A medida que w recorre la curva Γ de w0 a w0 , z recorrerá una curva γ en el plano z (que no pasará por z = 0) con la prescripción de que la rama concreta de z = w1/n (esto es, la solución de w = z n ) se elige por continuidad. Puesto que z 7→ w = z n es univaluada, γ también será una curva simple que no pasa por z = 0. Hay dos posibilidades: a) Que γ sea también una curva cerrada. Esto ocurre si Γ no encierra el origen w = 0. Puede ocurrir que para mantener la continuidad de z = w1/n haya que tomar una rama distinta de la inicial, pero después se vuelve a la misma y γ es cerrada. (Véase la fig. 22.) b) Que γ sea una curva abierta. Esto ocurre cuando Γ encierra el origen w = 0. El argumento de w crece de θ0 a θ0 + 2π y el argumento de z pasa de θ0 /n a (θ0 + 2π)/n. Es decir, z pasa de z0 = (w1/n )k ∈ Gk a z0′ = ei2π/n z0 = (w1/n )k+1 ∈ Gk+1 (con el convenio Gn = G0 ). (Véase la fig. 23.) Más generalmente, si Γ es una curva cerrada pero no necesariamente simple que no pasa por 0, y ℓ 80 y D2 w=z 6 E D1 D0 D3 D4 v x u D5 plano z plano w Figura 20: Descomposición alternativa de w = z 6 en dominios de univalencia. El recorrido es el plano complejo cortado según el semieje real negativo. es el ı́ndice de Γ respecto de w = 0, (es decir, Γ rodea ℓ veces el origen) θ0 pasa a θ0 + 2πℓ y se pasa de la rama k a la rama k + ℓ de w1/n . Este resultado es independiente de la elección concreta del corte de rama. Una forma práctica de contar ℓ es contar el número de veces (con su signo) que Γ cruza el corte de rama C. Definición. Sea una función multivaluada ϕ, con sus varias ramas, y η un punto de su dominio de definición.38 Se dice que η es un punto de ramificación de ϕ si una vuelta Γ alrededor de η produce un cambio de rama de la función, siendo Γ cualquier curva cerrada simple contenida en un entorno reducido arbitrariamente pequeño de η (y eligiendo la imagen por continuidad). Si n vueltas alrededor de η llevan cada rama sobre sı́ misma, se dice que η es un punto de ramificación de orden n − 1. (Se entiende el menor n positivo para el que esto ocurra.) Es decir, cuando al recorrer Γ n veces en el plano w la imagen es una curva cerrada en el plano z. Los puntos de ramificación son intrı́nsecos a la función multivaluada y no dependen de cómo se elija su ramificación. Se deduce que w = 0 es un punto de ramificación de la función multivaluada w1/n de orden n − 1. También w = ∞ es un punto de ramificación de esta función: En la esfera de Riemann el ∞ corresponde al polo norte N . Una curva cerrada que rodee N y que sea pequeña en la esfera de Riemann define una curva cerrada grande en el plano complejo. Esta curva rodea necesariamente w = 0 y por tanto cambia de rama de la función w1/n . Se deduce que ∞ es otro punto de ramificación de la función, y también de orden n − 1. Además no hay otros puntos de ramificación ya que si Γ 38 Más exactamente, un punto tal que admita algún entorno reducido contenido en el dominio de definición. 81 w=e z C c1 c0 c1 c2 plano z plano w Figura 21: Plano w: corte rama de log w a lo largo del arco C. Plano z: réplicas de C, ck que delimitan los dominios de univalencia en esta ramificación. Las curvas ck están desplazadas respecto de una de ellas, c0 , por 2πik. no encierra el origen no hay cambio de rama. El corte de rama une los dos puntos de ramificación, 0 e ∞. El análisis de la función multivaluada log w es similar: dado que z = log w = log |w| + i arg w, si una curva cerrada Γ rodea w = 0 un número ℓ ∈ Z de veces, el argumento cambia en 2πℓ y el logaritmo en 2πiℓ. (Véase la fig. 24.) Se deduce que w = 0 y w = ∞ son los únicos puntos de ramificación de log w. A diferencia de la función w1/n , los puntos de ramificación de log w son de orden infinito (también llamados de tipo logarı́tmico), ya que la imagen γ de la curva cerrada Γ nunca es ella misma una curva cerrada si ℓ 6= 0. √ Otra función multivaluada es, por ejemplo, z = w2 − 1 con puntos de ramificación w = ±1 (pero no ∞). Tiene dos ramas y el corte de rama se puede elegir a lo largo del intervalo [−1, 1]. Una curva cerrada Γ que no pase por w = ±1, rodeará ℓ1 veces w = 1 y ℓ−1 veces w = −1. γ es cerrado en el plano z (y por tanto no hay cambio de rama) sii ℓ1 + ℓ−1 es par. (Véase la fig. 25.) 9.3. Superficies de Riemann Una función multivaluada puede considerarse univaluada generalizando su dominio de definición. El procedimiento se puede ilustrar mediante la función log w que tiene infinitas ramas, tantas como 82 v z=w w0 * 1/6 y γ *z0 Γ x u plano w plano z Figura 22: Camino cerrado Γ en el plano w y su imagen γ en el plano z = w1/6 . Γ no rodea w = 0 y γ es cerrado. números enteros. Por cada una de estas ramas, tomemos una copia de su dominio E = C−{u ≥ 0}. Estas copias las denotamos Ek , k = 0, ±1, ±2, . . . y se denominan hojas de Riemann. E es el plano complejo w cortado (como con una tijera) por el semieje real positivo. El corte produce dos bordes, el superior δ + y el inferior δ − . Sean δk+ y δk− los bordes superior e inferior de la hoja Ek . (Véase la fig. 26.) Con las infinitas hojas se procede a formar una nueva superficie identificando (o pegando) los + bordes δk− ≡ δk+1 para todos los k. La superficie S ası́ obtenida se denomina superficie de Riemann de la función log w. (Véase la fig. 27.) La idea es que la hoja E0 representa a los puntos con argumento entre 0 y 2π (ambos excluidos), E1 a los puntos con argumento entre 2π y 4π, y en general, Ek a los puntos tales que 2πk < arg w < 2π(k + 1). Ası́ δk+ son los puntos con arg w = 2πk, δk− son los puntos con arg w = 2π(k + 1) y + naturalmente está identificado con δk+1 , que también son los puntos con arg w = 2π(k+1). Después de identificar los bordes, S es una superficie perfectamente suave y regular también en las uniones. Además la misma superficie se obtiene independientemente de dónde estuviera originalmente el corte de rama.39 39 Identificar puntos es un método estándar para formar nuevas variedades a partir de otras dadas. Por ejemplo, si en el disco cerrado {|z| ≤ 1} se identifican todos los puntos de su frontera, |z| = 1, se obtiene una superficie topológicamente equivalente a la superficie de una esfera. A partir del plano complejo se obtuvo la esfera de Riemann al identificar todos los puntos del infinito (en todas la direcciones). Si en la tira {z 0 ≤ Re z ≤ 1} se identifican cada punto (0, y) con (1, y) se obtiene un cilindro. 83 v Γ z=w w0 * 1/6 y z0 * γ *z0 u x plano w plano z Figura 23: Camino cerrado Γ en el plano w y su imagen γ en el plano z = w1/6 . Γ rodea una vez w = 0 y γ empieza en una rama de la función y acaba en la rama siguiente. z0′ = e2πi/6 z0 S está compuesta por las hojas de Riemann con los bordes identificados. La superficie de Riemann extendida S ∗ se obtiene al añadir el 0 y el ∞, que son puntos comunes a todas las hojas. Hay una proyección canónica de S en C: a cada punto de S le corresponde un número complejo y cada punto en C − {0} le corresponden infinitos puntos en S (llamados réplicas), una réplica en cada hoja de Riemann. Localmente la superficie de Riemann del logaritmo y el plano complejo son iguales: si se considera un entorno pequeño de un punto w en S o en C − {0} no se ve diferencia. Globalmente son variedades distintas: por ejemplo, S es simplemente conexo40 mientras que C − {0} no lo es. La diferencia esencial entre S y C − {0} es que en C − {0}, cada punto w tiene infinitos argumentos, o equivalentemente un argumento definido módulo 2π. En cambio en S, cada punto tiene exactamente un argumento θ ∈ R. En S los puntos con coordenadas polares (r, θ) y (r, θ + 2πk) son puntos distintos si k 6= 0, ambos con la misma proyección en C. Es decir, la función arg w es univaluada en S. En S se puede definir la función log w de forma natural por la fórmula log w = log |w| + i arg w. Dado que argumentos distintos corresponden a puntos distintos de S la función log w es univaluada en S. Con el fin de generalizar la construcción para otras funciones, se puede considerar el siguiente procedimiento equivalente: se toma un punto w0 fijo cualquiera de S (que no sea 0 o ∞) y se le 40 En efecto, ya que cualquier camino cerrado en S se puede contraer dentro de S a un punto. Obsérvese que en S no hay curvas cerradas que encierren a 0. 84 y v z= log w z ∗ 0 2πi E w0 * 0 x u Γ ∗ z0 2πi plano w plano z Figura 24: En el plano w: curva Γ que rodea w = 0 dos veces. Plano z: su imagen bajo z = log w (eligiendo la rama del logaritmo por continuidad) pasa del dominio de univalencia G−1 a G1 . z= (w−1)(w+1) Γ1 Γ2 1 γ1 γ2 1 *w0 z0 plano w *z 0 plano z √ Figura 25: El intervalo [−1, 1] es el corte rama de z = w2 − 1. Γ1 tiene ℓ1 = ℓ−1 = 1 y no cambia de rama. Γ2 tiene ℓ1 = 1, ℓ−1 = 0 y pasa de una rama a la otra. En ambos casos z se va eligiendo por continuidad a lo largo de la curva. 85 E2 δ2 δ2 δ1 + δ0 E1 + E0 δ1 v + δ0 u Figura 26: Copias del plano w cortado a lo largo del semieje real positivo. 0 S v u Figura 27: Superficie de Riemann de log w (w = 0 es común a todas hojas.) 86 hace corresponder una cualquiera de sus imágenes z0 = log w0 . Entonces para cualquier otro punto w ∈ S se toma un arco Γ en S que conecte w0 con w y que no pase por 0. La imagen z = log w correspondiente a w se asigna por continuidad siguiendo la imagen γ de Γ desde z0 hasta z. El resultado no depende del arco Γ elegido ya que la imagen final z sólo depende del argumento final de w. Este argumento es un valor fijo (que depende de la proyección de w en C) más un 2πℓ. Cada valor de ℓ corresponde a una rama distinta de log w y también a una hoja distinta de S. De este modo la función log w definida sobre S es univaluada ya que imágenes distintas corresponden a originales distintos. La función ası́ definida41 es analı́tica en S. Los puntos de ramificación son puntos no regulares por definición. Estos son los únicos puntos singulares. log w : S → C es univalente, y 1 tiene derivada . w Nota: La idea que se puede abstraer para una función multivaluada cualquiera ϕ(w) es la siguiente: en C para determinar el valor de la función en un punto w tómese un punto fijo w0 y una de sus imágenes ϕ(w0 ), y considérese un camino que vaya de w0 a w (y que no pase por los puntos de ramificación). Los caminos que rodeen los puntos de ramificación de la misma forma son equivalentes y producen el mismo valor de ϕ(w) (eligiendo la rama por continuidad). Caminos que rodeen los puntos de ramificación de forma distinta pueden llevar a otras ramas de la función y en este caso son caminos inequivalentes al original. Por tanto en C importa el punto w al que se llega y también cómo se llega. En cambio, en la superficie de Riemann de ϕ(w), no importa cómo se llega a un punto: lo que serı́an dos caminos inequivalentes en C directamente llevan a dos puntos distintos de la superficie de Riemann. La función pasa a ser univaluada por construcción. Además esta construcción sólo depende de la función multivaluada y no de cómo se descomponga en ramas. Para la función w1/n la construcción de su superficie de Riemann S es análoga excepto que − + , . . . , δn−1 ≡ δ0+ . (Esto hay n hojas E0 , E1 , . . . , En−1 con identificación δ0− ≡ δ1+ , . . . , δk− ≡ δk+1 corresponde a la superficie de Riemann de log w pero identificando las hojas módulo n.) Después de n vueltas alrededor de w = 0 se vuelve al mismo punto de S. En este caso S recubre n veces al plano complejo. De nuevo w1/n : S → C − {0} es univalente, y 0, ∞ son los únicos puntos donde la función no es analı́tica. √ Ejemplo. Para la función z, z = 0, ∞ son los puntos de ramificación. Cada vez que Γ rodea z = 0 se cambia de rama, después un número par de vueltas se vuelve a la misma rama. El corte de rama se puede tomar según el semieje real positivo. La superficie de Riemann recubre dos veces C. Se obtiene con dos copias de C cortadas identificando el borde superior de cada hoja con el inferior 87 z z0∗ hoja 1 γ z δ1 hoja 2 γ δ2 δ2 δ1 √ Figura 28: Hojas de Riemann para z. (La hoja 1 ha sido etiquetada arbitrariamente como √ √ z y la hoja 2 como − z.) El borde etiquetado como δ1 de la hoja 1 está identificado con el borde δ1 de la hoja 2, y lo mismo los bordes δ2 . La curva γ empieza en el punto z0 de la hoja 1, rodeando z = 0 llega al borde δ2 y pasa a la hoja 2, luego rodeando otra vez w = 0 llega al borde δ1 y vuelve a la hoja 1 y a z0 . γ es una curva cerrada simple en la superficie de Riemann. La proyección de γ sobre C es una curva cerrada que rodea w = 0 dos veces. de la otra. (Véase la fig. 28.) √ √ z − i+ z + i tiene cuatro hojas, correspondientes a las cuatro opciones Ejemplo. La función √ √ ± z − i y ± z + i. Los puntos de ramificación son z = ±i e ∞, todos de orden 1. Los cortes de rama se pueden tomar a lo largo de los semiejes {z = x + i , 0 ≤ x ≤ +∞} y {z = x − i , 0 ≤ x ≤ +∞}. Las cuatro hojas se pegan como se indica en la fig. 29. 9.4. Integración y funciones multivaluadas En la Sec. se mostró que una función analı́tica f (z) en un dominio simplemente conexo G tiene una primitiva, única salvo constante aditiva, que es su integral indefinida Z z F (z) = F (z0 ) + f (z) dz z0 , z ∈ G (9.7) z0 donde la integral es sobre una curva suave a trozos C contenida en G que una un punto fijo z0 con un punto cualquiera z de G. La integral no depende de la curva. 41 La función no depende en realidad de la elección (w0 , z0 ) inicial ya que todas las hojas son idénticas hasta que se decide qué logaritmo le corresponde a w0 . 88 + z−i + z+i i i + hoja 1 z−i + z+i 1 2 i 3 i 4 hoja 3 z−i z+i hoja 2 2 1 5 6 hoja 4 z−i z+i i 7 8 i 8 7 i 4 3 i 6 5 √ √ Figura 29: Hojas de Riemann para z − i + z + i. Los bordes se pegan como se indica: el borde superior 1 (en la hoja 1) se identifica con el borde inferior 1 (en la hoja 2), etc. 1 , que es analı́tica en todo el plano complejo excepto z = 0, podemos z tomar como dominio Gp = C − {x ≥ 0} que es simplemente conexo, y una curva Cp ⊂ Gp . Una 1 primitiva de f (z) = en este dominio es Log z y por aplicación del teorema z Z z 1 dz , C p ⊂ Gp . (9.8) Log z = Log z 0 + z0 ,Cp z Para la función f (z) = Teniendo en cuenta que Arg z ∈ [0, 2π[, Log 1 = 0 se puede alcanzar tomando el lı́mite z0 → 1 desde el semiplano superior (es decir, el semiplano { Im z > 0})42 y se puede escribir Z z 1 dz , C p ⊂ Gp . (9.9) Log z = lı́m z0 →1 z z ,C p 0 Im z >0 0 (El lı́mite es necesario ya que 1 no pertenece al dominio Gp .)43 Esto es equivalente a tomar una 42 El lı́mite z0 → 1 desde el semiplano inferior da, en cambio, Log z 0 → 2πi. La función Log z no es continua a lo largo del semieje real positivo. 43 O también Z z 1 dz , Cp ⊂ Gp . Log z = z + 1+i0 ,Cp 89 C 1 0 C 2 C1 z Figura 30: La curva C proporciona Log z mediante Log z − 2πi, respectivamente. Z C 1 dz. C1 y C2 producen Log z + 2πi y z curva C que empiece en 1, siga hacia arriba inicialmente y luego siga hasta un punto cualquiera z (no nulo) sin cruzar el semieje real positivo en ningún momento. (Nótese que si C empieza en 1 pero sigue hacia abajo inicialmente sin cruzar después el semieje real positivo hasta alcanzar z, se obtiene otro resultado, a saber, Log z − 2πi.) Si C se corta según otros semiejes se obtienen otras determinaciones del arg z y del log z. Si en vez de restringirnos al plano complejo cortado permitimos curvas C que unan z0 = 1 con z por cualquier camino (pero excluyendo z = 0 para garantizar que la integral exista) se obtiene Z z 1 dz = Log z + 2πin = log z (0 6∈ C) (9.10) 1,C z siendo n el número de veces (con su signo) que z = 0 es rodeado por el camino cerrado γ que se obtiene al recorrer C y luego volver por un camino canónico Cp (es decir, un camino contenido en el plano cortado según el semieje real positivo).44 En resumen, si para la función 1/z, univaluada 44 En efecto, 2πin = Z γ 1 dz = z Z C 1 dz − z 90 Z Cp 1 dz = log z − Log z . z (9.11) pero singular en z = 0, se busca una primitiva en el dominio G = C − {0}, que no es simplemente conexo, se obtiene la función primitiva multivaluada log z obteniéndose ramas distintas al seguir caminos inequivalentes (con distinto n). (Véase la fig. 30.) 1 definida sobre la superficie de Riemann de la función logaritmo, S (tomando z el mismo valor en todas las réplicas) la fórmula Z z 1 log z = dz (9.12) 1 z Si se toma f (z) = (sobre cualquier curva C ⊂ S que una 1 con z) es directamente correcta, ya que S es un dominio simplemente conexo: caminos en S que son inequivalentes al proyectarlos sobre C acaban en puntos distintos en la superficie de Riemann y no hay multivaluación en S. Aquı́ 1 ∈ S es la réplica de 1 ∈ C tal que log 1 = 0. α β + es similar: f (z) es analı́tica en G = C−{a}−{b} z−a z−b que no es simplemente conexo. Gp = C − {a + t, t ≥ 0} − {b + t, t ≥ 0} es simplemente conexo y define una primitiva univaluada, F (z) = α Log (z − a) + β Log (z − b). Si se integra en G se obtiene F (z) = α log(z − a) + β log(z − b). La multivaluación es del tipo (αn1 + βn2 )2πi, correspondiente al número de vueltas del camino de integración C alrededor de z = a y z = b comparado con un camino Cp fijo. En la superficie de Riemann hay una hoja por cada valor de n1 y de n2 (para α, β genéricos, concretamente, no conmensurables, y a 6= b). El análisis para la función f (z) = Finalmente consideremos la integral indefinida de una función multivaluada. Sea f (z) = log z, cuya primitiva es F (z) = z log z − z. Estas funciones son multivaluadas en C pero univaluadas y analı́ticas en S, la superficie de Riemann del logaritmo. Consideremos la integral a lo largo de la circunferencia Cρ = {z(t) = ρ eit , 0 < t < 2π} (ρ > 0): Z I= f (z) dz . (9.13) Cρ Cuando f (z) es analı́tica en Cρ y en su interior, I = 0. Cuando f (z) es analı́tica fuera del disco 1 |z| < r, el resultado no depende de ρ, siempre que ρ > r, (por ejemplo, para f (z) = , I = 2πi). z En cambio si tomamos f (z) = Log z, I = lı́m (z Log z − z) − lı́m (z Log z − z) = 2πiρ . z→ρ z→ρ Im z<0 Im z>0 91 (9.14) El resultado depende de ρ. El motivo es que o bien se trabaja con el plano cortado y Log z es no analı́tica en el semieje real positivo, o bien se trabaja en la superficie de Riemann. En este caso log z es analı́tica fuera de z = 0 pero entonces Cρ no es cerrado, ya que sobre la superficie de Riemann Cρ empieza y acaba en puntos distintos. En otros casos, como por ejemplo log2 z, el resultado depende no sólo de ρ sino también del punto donde empieza y acaba el recorrido. 92 10. 10.1. Sea Series de Taylor Desarrollo de una función analı́tica P∞ n=0 cn (z − a)n una serie con radio de convergencia R > 0. Como se vio, la función s(z) = ∞ X n=0 cn (z − a)n , (10.1) definida en su región de convergencia, es analı́tica en el disco |z − a| < R. A su vez, dada la suma de la serie, s(z), podemos determinar los coeficientes, cn : Por el teorema de Weierstrass, las derivadas sucesivas de s(z) se obtienen derivando término a término: s(k) (z) = ∞ X n=k ∞ X (n + k)! n! cn (z − a)n−k = cn+k (z − a)n , (n − k)! n! n=0 (10.2) y en particular, s(k) (a) = k! ck , es decir cn = y por tanto, s(z) = s(n) (a) . n! ∞ X s(n) (a) n=0 n! (z − a)n . (10.3) (10.4) Se deduce que la serie queda unı́vocamente determinada por su suma. Obsérvese que los coeficientes se pueden determinar también integrando, en lugar de derivando, mediante la fórmula integral de Cauchy (véase la ecuación (10.6)). Teorema. (Desigualdades de Cauchy.) Sea s(z) la suma de una serie de potencias centrada en a con radio de convergencia R > 0. Y sea |s(z)| ≤ K en el disco |z − a| < ρ (0 < ρ ≤ R). Entonces, (n) s (a) K n = 0, 1, 2, . . . (10.5) n! ≤ ρn , 93 Demostración: Sea γr la circunferencia de radio r, 0 < r < ρ centrada en a y orientación positiva, entonces, por la fórmula integral de Cauchy, Z s(z) n! (n) dz, n = 0, 1, 2, . . . (10.6) s (a) = 2πi γr (z − a)n+1 Dado que K es una cota de s(z) en el disco |z − a| < ρ que contiene a γr se deduce |s(n) (a)| ≤ n! K n! K 2πr = n n+1 2π r r ∀r < ρ, (10.7) y en consecuencia se obtiene (10.5) que es la mejor de las cotas. ♦ P∞ n La serie n=0 cn (z − a) define una función analı́tica en z = a (siempre que el radio de convergencia sea no nulo). Veamos un recı́proco: Teorema. Sea f (z) analı́tica en el disco abierto Dρ = {z |z − a| < ρ} para cierto ρ > 0. Entonces, f (z) admite desarrollo en serie de Taylor en Dρ , es decir, f (z) = ∞ X f (n) (a) n=0 n! (z − a)n , ∀z ∈ Dρ . (10.8) Y por tanto R ≥ ρ, siendo R el radio de convergencia de la serie. Los cn = f (n) (a)/n! son los coeficientes del desarrollo en serie de Taylor de f (z) en torno a z = a. Demostración: Sea 0 < r < ρ, γr la circunferencia de radio r y centro a (con orientación positiva) y |z − a| < r, Z Z 1 f (ζ) f (ζ) 1 1 dζ dζ = f (z) = z−a 2πi γr ζ − z 2πi γr ζ − a 1− ζ −a Z Z ∞ ∞ n X f (ζ) X z − a f (ζ) 1 n 1 dζ dζ = (z − a) = 2πi γr ζ − a n=0 ζ − a 2πi γr (ζ − a)n+1 n=0 = ∞ X f (n) (a) n=0 n! (z − a)n . (10.9) z − a < 1 para justificar el desarrollo. Dado que f (ζ) es continua En la tercera igualdad se usa que ζ − a en γr , está acotada y la convergencia es uniforme. Esto justifica integrar término a término. La igualdad (10.9) vale para todo z tal que |z − a| < r y todo r < ρ, por tanto ∀z en |z − a| < ρ. ♦ 94 Notas: : 1) Toda función analı́tica lo es en algún disco por pequeño que sea, y se aplica el teorema. 2) El teorema no afirma que f (z) sea analı́tica en todo su disco de convergencia DR = {|z −a| < R} (en cuyo caso coincidirı́a con la suma de la serie). Por ejemplo la función z e , z 6= 1 f (z) = (10.10) 0, z = 1 es analitica en el disco |z| < 1 y ahı́ coincide con la suma de su serie de Taylor, con radio de convergencia infinito, pero no es analı́tica en z = 1. En general la función f (z) estará definida en un dominio mayor, E, tal que Dρ ⊂ E y la serie y la función pueden no coincidir fuera de Dρ . El teorema implica que si f (z) y s(z) no coinciden en todo DR , f (z) no puede ser analı́tica en todo DR . 3) El teorema implica que si f (z) es derivable en el entorno de un punto como función compleja, automáticamente también es analı́tica en el sentido de desarrollable en serie de potencias con radio de convergencia no nulo. La misma propiedad no es válida para funciones reales. 1 Ejemplo. f (x) = e− |x| , x ∈ R, es derivable (infinitas veces) en todo R, sin embargo no es analı́tica. En efecto, f (n) (0) = 0, n = 0, 1, 2, 3, . . . por tanto la suma de la serie de Taylor alrededor de x = 0 es idénticamente cero aunque la función no es idénticamente cero en un entorno de x = 0. 10.1.1. Sobre el cálculo de series de Taylor En principio los coeficientes se pueden calcular sistemáticamente tomando sucesivas derivadas de la función f (z), tal como se indica en (10.3). Sin embargo, esta no es la única opción y en muchos casos lo mejor es usar desarrollos de funciones conocidas que aparezcan en f (z). Ejemplo. Sea f (z) = cos z . Calcúlese su desarrollo en serie de Taylor en torno a z = 0 1 + sen(z 2 ) hasta orden z 3 inclusive. Solución: En este caso las sucesivas derivadas producen expresiones cada vez más complicadas. El resultado se obtiene más fácilmente usando los desarrollos conocidos de las funciones seno y coseno: 1 1 (10.11) sen w = w − w3 + · · · , cos w = 1 − w2 + · · · . 3! 2! 95 Denotando O(z n ) los términos del tipo an z n + an+1 z n+1 + · · · , se tiene 1 − 21 z 2 + O(z 4 ) cos z f (z) = = 1 + sen(z 2 ) 1 + z 2 + O(z 4 ) 3 1 = (1 − z 2 + O(z 4 ))(1 − z 2 + O(z 4 )) = 1 − z 2 + O(z 4 ) . 2 2 (10.12) En la tercera igualdad se ha usado el desarrollo de Taylor de 1/(1 − w): 1 = 1 + w + O(w2 ). 1−w (10.13) Nota: Es importante notar que O(z n ) representa distintas series en cada caso. Es decir, f (z) = O(z 3 ) y g(z) = O(z 3 ) no implica f (z) = g(z). O(z n ) representa cualquier serie con aj = 0 si j < n, por tanto, z m O(z n ) = O(z n+m ) y también O(z n )O(z m ) = O(z n+m ), y (O(z n ))m = O(z nm ), etc. ♦ 10.2. Puntos regulares y singulares Definición. Si en z0 la función f (z) es analı́tica, se dice que z0 es un punto regular de f (z), en otro caso se dice que z0 es un punto singular de f (z) (incluidos los puntos en los que f (z) no está definida.) Ejemplo. Los puntos de ramificación de una función multivaluada son puntos singulares. Los puntos a, b son puntos singulares de 1/((z − a)(z − b)). Teorema. Sea f (z) analı́tica en z = a, con radio de convergencia R < ∞. Si f (z) es analı́tica en todo el disco {|z − a| < R}, entonces necesariamente tiene algún punto singular en la frontera {|z − a| = R}. Demostración: Si f (z) fuera analı́tica en todos los puntos |z −a| ≤ R, habrı́a un disco mayor45 {|z − a| < ρ}, ρ > R, en el cual también serı́a analı́tica y por tanto coincidirı́a con su desarrollo en serie de Taylor en un disco de radio mayor que R, en contra de la hipótesis de que R es el radio de convergencia. 45 Si la función es analı́tica en todos los puntos de la circunferencia |z − a| = R lo será también en entornos de estos puntos y por el teorema de Heine-Borel la circunferencia se podrá recubrir con un conjunto finito de tales entornos. De ahı́ que la función serı́a analı́tica en un disco mayor. 96 1 , x ∈ R, su desarrollo en serie de potencias en torno a 1 + x2 x = 0, 1 − x2 + x4 − x6 + · · · , deja de converger cuando |x| ≥ 1 sin razón aparente, ya que la función es perfectamente bien comportada para todo x real. Esto se entiende yendo al plano 1 complejo: f (z) = es analı́tica excepto en z = ±i. Por lo tanto es analı́tica en el disco 1 + z2 |z| < 1 y necesariamente R ≥ 1. Si R fuera mayor que 1 la suma de la serie serı́a analı́tica en z = i. 1 en el disco |z| < 1 y el lı́mite cuando z → i Eso es imposible porque la suma de la serie es 1 + z2 es ∞. Se deduce que R = 1. Ejemplo. Para la función real Nota: El teorema no afirma que una función f (z) analı́tica en z = a con radio de convergencia finito R en su serie de Taylor tenga necesariamente que ser singular en algún punto de |z − a| = R. Por ejemplo la función 1 , |z| < 21 (10.14) f (z) = 1−z 0, z ≥ 12 analı́tica en z = 0 con R = 1 es también analı́tica en |z| = 1. Como regla, el radio de convergencia llega hasta la singularidad más próxima, a menos que esa singularidad se pueda evitar redefiniendo la función de modo que sea analı́tica en un dominio mayor. Singularidades que no se pueden evitar son, entre otras, polos (el lı́mite existe pero es infinito), singularidades esenciales (el lı́mite no existe) y puntos de ramificación. √ Ejemplo. Si f (z) = z con el corte de rama en el semieje R+ , y se desarrolla en torno a z = 1 + i, la singularidad más próxima está en z = 1 (el punto más próximo sobre el √ corte de rama, sobre el cual la función es singular), pero el radio de convergencia es R = |1 + i| = 2. El desarrollo en serie no ve el corte de rama sino que se extiende por la superficie de Riemann, y la singularidad que determina R es el punto de ramificación z = 0. Nótese que aunque f (z) tiene lı́mite en z = 0, su primera derivada ya diverge, y el radio de convergencia es común a f (z) y todas sus derivadas. Ejemplo. Si se desarrolla en torno a z = 1 la función f (z) = z/(ez − 1), las singularidad más próxima está en z = 0 ya que ahı́ la función no está definida (indeterminación de tipo 0/0), sin embargo esta singularidad se puede eliminar definiendo f (0) = 1. El radio de convergencia es R = |2πi − 1| (ez − 1 se anula en 2πin, n ∈ Z). Teorema. (Teorema de Liouville.) Si f (z) es entera y acotada entonces debe tomar un valor constante sobre todo el plano complejo. Demostración: Si f (z) no tiene puntos singulares en C entonces será desarrollable en serie en 97 torno a 0 (por ejemplo) con radio de convergencia infinito ∀z ∈ C f (z) = ∞ X cn z n . (10.15) n=0 Además por hipótesis |f (z)| < K para cierto K > 0. Por las desigualdades de Cauchy |cn | < pero R = ∞. Esto implica que cn = 0 para todos los n excepto c0 . Es decir, f (z) = c0 . ♦ K , Rn Nota: El teorema de Liouville implica que una función no puede ser regular (en el sentido complejo) en todos los puntos, incluido el ∞, a menos que sea trivial (constante). Esto no ocurre para funciones reales. Por ejemplo, f (x) = 1/(1 + x2 ) es regular en todo el eje real (incluido el infinito). 10.3. Teoremas de unicidad Teorema. Sean f (z) y g(z) dos funciones analı́ticas en un disco abierto D centrado en z0 y sea E ⊂ D tal que z0 es un punto de acumulación de E. Entonces, si f (z) = g(z) para todo z de E también f (z) = g(z) en todo el disco D. Demostración: Por ser analı́ticas, f (z) y g(z) admiten desarrollo en serie de Taylor en D (es decir, coinciden con las sumas de sus series de Taylor en D). Se va a probar que los coeficientes del desarrollo están determinados exclusivamente por el valor de las funciones en E. Como las dos funciones coinciden en E los coeficientes del desarrollo serán idénticos y por tanto las dos funciones coincidirán en D. En efecto, f (z) = ∞ X n=0 cn (z − z0 )n , z ∈ D. (10.16) f (z) es continua en z0 y este punto se puede alcanzar tomando el lı́mite dentro de E, es decir, c0 = f (z0 ) = lı́m f (z) = lı́m f (z). z→z0 z→z0 (10.17) z∈E Para obtener c1 definimos ∞ f (z) − f (z0 ) X f1 (z) = = cn+1 (z − z0 )n , z − z0 n=0 98 (10.18) z C z z1 z2 z3 0 G Figura 31: Extensión analı́tica a base de discos centrados en una curva C que une el punto fijo z0 con un punto cualquiera z del dominio G. f1 (z) es analı́tica en D, por tanto c1 = f1 (z0 ) = lı́m f1 (z). z→z0 (10.19) z∈E Los demás coeficientes se obtienen definiendo sucesivamente fn (z) = (fn−1 (z)−fn−1 (z0 ))/(z −z0 ), de modo que cn = fn (z0 ) se obtiene con valores sólo en E. ♦ Teorema. (Unicidad de funciones analı́ticas.) Sean f (z) y g(z) dos funciones analı́ticas en un mismo dominio G, y supongamos que f (z) = g(z) en los puntos de un subconjunto E de G, tal que E tiene un punto lı́mite z0 ∈ G. Entonces f (z) = g(z) ∀z ∈ G. Demostración: Sea z un punto cualquiera de G y C un arco de z0 a z contenido en G. Sea ρ la distancia de C a la frontera de G o bien un valor positivo arbitrario si G = C. Se deduce que los discos abiertos de radio ρ centrados en puntos de C estarán contenidos en G. Ahora sean zk , k = 1, . . . , N puntos consecutivos de C tales que zN = z y |zk − zk−1 | < ρ. [Esto siempre es posible: si |z − z0 | < ρ ya está, con N = 1. Si no, sea 0 < r < ρ y sea z1 una intersección de C con la circunferencia de radio r centrada en z0 . Se repite la construcción tomando como centro z1 para obtener z2 a distancia r, y ası́ sucesivamente, acabando en ZN = z. El N requerido es finito ya que la longitud de C es finita y es mayor que rN .] Sean Dk los discos de radio ρ centrados en los zk . Por el teorema de unicidad en discos, las dos funciones coinciden en D0 y en particular en un 99 entorno de z1 ∈ D0 . Por tanto también coinciden en D1 . Repitiendo el argumento para zk ∈ Dk−1 , se obtiene que las funciones coinciden en z, para todo z de G. ♦ Nota: Este resultado es muy fuerte ya que implica que una función analı́tica en un dominio G queda completamente determinada por su valor sobre un pequeño entorno de un punto, o sobre un trozo de curva, por pequeño que sea. En particular, si f (z) se anula sobre un arco será idénticamente 0 en todo G (siendo G un dominio que contenga al arco y en el que f (z) sea analı́tica). La fórmula integral de Cauchy permitı́a reconstruir una función analı́tica en el interior de una curva cerrada si se conocı́a sobre la curva. Aquı́ se ve que en realidad basta un arco cualquiera de la curva para que la función quede unı́vocamente determinada. Por otra parte el teorema también nos indica la poca flexibilidad y limitaciones de las funciones analı́ticas. Por ejemplo, si f1 (x) es una función de [a1 , b1 ] en R infinitamente diferenciable (de clase C ∞ ) y f2 (x) de [a2 , b2 ] en R, con b1 < a2 , también C ∞ , es posible definir f (x) C ∞ no única, en [a1 , b2 ] tal que coincida con f1 y con f2 en sus respectivos intervalos. Una construcción análoga no es posible en general para funciones analı́ticas (de variable real o compleja), ya que la función f1 en el primer dominio determinarı́a f en el segundo dominio y allı́ podrı́a no coincidir con f2 . 10.4. Ceros de una función analı́tica Definición. Sea f (z) una función compleja. Un punto z0 es un cero de f (z) si f (z0 ) = 0. Si f (z) es analı́tica en un entorno de z0 y no idénticamente nula, entonces no todos los coeficientes de su desarrollo de Taylor en torno a z0 pueden se nulos. Si m es el primer valor de n tal que cn 6= 0 se dice que z0 es un cero de orden m de f (z) y en este caso f (z) = cm (z−z0 )m +· · · = (z−z0 )m g(z) siendo g(z) otra función analı́tica con el mismo radio de convergencia y tal que g(z0 ) 6= 0. Cuando m = 1 se dice que z0 es un cero simple, en otro caso es múltiple. Si z0 es un cero de orden m, f (n) (z0 ) = 0 para n < m y f (m) (z0 ) 6= 0. Ejemplo. Para f (z) = z 2 (z − 1), z = 0 es un cero doble y z = 1 es un cero simple. Teorema. Si f (z) es una función analı́tica en un dominio G en el cual no es idénticamente nula, sus ceros en G son aislados. (Es decir, todo cero z0 admite un entorno en el que no hay otros ceros de f (z).) Demostración: Si los ceros no fueran aislados f (z) se anuları́a en un conjunto E (el conjunto de los ceros de f (z)) con z0 como punto de lı́mite y en este caso la función serı́a idénticamente cero. Ejemplo. Para f (z) = sen(1/z) los ceros están en zn = 1/(πn), n ∈ Z, con punto de 100 acumulación z = 0. Sin embargo, no hay contradicción ya que sen(1/z) no es analı́tica en z = 0. 10.5. Principio del módulo máximo Teorema. (Principio del módulo máximo.) Si f (z) es analı́tica y no constante en un dominio G entonces no existe un z0 ∈ G tal que |f (z0 )| ≥ |f (z)| ∀z ∈ G. Es decir, |f (z)| no alcanza un máximo en ningún punto de G. Demostración: Supongamos que para cierto z0 ∈ G |f (z0 )| ≥ |f (z)| ∀z ∈ G. Podemos suponer que f (z0 ) 6= 0, ya que en otro caso f (z) = 0, serı́a constante. Sea g(z) := f (z)/f (z0 ) = u(z) + iv(z) (u, v reales) entonces g(z0 ) = 1 ≥ |g(z)| ≥ |u(z)|. Por la fórmula integral de Cauchy (siendo γR un circunferencia contenida en G centrada en z0 , radio R y orientación positiva) Z Z 2π g(z) 1 1 dz = g(z0 + Reiθ ) dθ . (10.20) 1 = g(z0 ) = 2πi γR z − z0 2π 0 Para la parte real esto implicarı́a 1 0= 2π Z 0 2π 1 − u(z0 + Reiθ ) dθ . (10.21) Dado que 1 − u ≥ 0 y u es continua se deducirı́a que u = 1 sobre la circunferencia, y por tanto v = 0 (ya que 1 ≥ |g|2 = 1 + v 2 ). Es decir, g(z) = 1 serı́a constante sobre la circunferencia, y por tanto constante en todo el dominio, y lo mismo f (z). ♦ Corolario: Sea G un dominio acotado y sea Ḡ la correspondiente región cerrada (G junto con su frontera). Entonces, si f (z) es analı́tica en G y continua en Ḡ, |f (z)| tiene un máximo en la frontera. Demostración: Una función real continua siempre alcanza un máximo en un conjunto compacto. Puesto que el máximo no está en el interior de Ḡ tiene que estar en su frontera. Corolario: (Principio del módulo mı́nimo.) Si f (z) es analı́tica en G, no se anula en ningún punto y no es constante, entonces |f (z)| no puede tener un mı́nimo en G. Si f (z) es continua en Ḡ y esta región es acotada, el mı́nimo se alcanza en la frontera. Demostración: Basta aplicar el principio del módulo máximo y los corolarios a la función 101 1 . f (z) Dicho de otro modo, si f (z) es analı́tica, |f (z)| no tiene máximos locales. Si además no se anula tampoco puede tener mı́nimos locales. 102 11. Series de Laurent 11.1. Desarrollo de Laurent de una función analı́tica 11.1.1. Series de potencias negativas 1 . Si queremos una aproximación útil cuando |z| es 1+z pequeño podemos usar un desarrollo en serie de Taylor en torno a z = 0 Ejemplo. Sea la función f (z) = 1 = 1 − z + z2 − z3 + · · · , 1+z |z| < 1 . (11.1) La serie truncada proporciona una aproximación que mejora cuanto menor es |z| y cuantos más términos se retengan. Si se quiere una aproximación útil para z grande se puede hacer un desarrollo de Taylor en potencias de 1/z (que es pequeño si z es grande): 1 1 1 1 1 1 1 (11.2) = − 2 + 3 + ··· , para < 1 o sea |z| > 1 . 1 = 1+z z1+ z z z z z Es decir, una serie de potencias negativas. ♦ ∞ X 1 , sea r := lı́m |cn |1/n . Entonces la serie converge n n→∞ (z − a) n=0 absolutamente en |z − a| > r y diverge en |z − a| < r, siendo 0 ≤ r ≤ +∞. Teorema. Dada la serie cn 1 y aplicar los teoremas de la serie de Taylor a la serie z−a 1 de potencias en ζ, teniendo en cuenta que |z − a| ≶ r implica ζ ≷ . r Demostración: Basta tomar ζ = Nota: Es decir, para series de potencias negativas, hay convergencia absoluta en el exterior de un disco y divergencia en el interior, al contrario de lo que ocurre para series de potencias positivas. Cuando la serie de potencias negativas es finita, (es decir, todos los cn se anulan a partir de uno dado) r = 0 y la suma es analı́tica en todo el plano complejo excepto quizá z = a. Definición. Una serie de potencias con potencias positivas y negativas se denomina serie de Laurent. La parte de potencias no negativas es la parte regular de la serie. La parte de potencias 103 y z + r a x 0 Figura 32: La zona sombreada es el dominio de convergencia de la serie de potencias negativas. negativas es la parte principal. ∞ X n=−∞ n cn (z − a) := ∞ X n=0 n cn (z − a) + Parte regular ∞ X m=1 c−m 1 . (z − a)m (11.3) Parte principal La serie de Laurent converge, por definición, sii las partes regular y principal convergen. Teorema. Dada una serie de Laurent, sea R = 1 y sea r = lı́m |c−m |1/m . Entonces, m→∞ lı́m |cn |1/n n→∞ si r < R, a) la serie converge absolutamente en el dominio G = {r < |z − a| < R} ( corona circular de convergencia absoluta, véase fig. 33). b) la serie es uniformemente convergente en todo subconjunto compacto de G, y c) la suma es analı́tica en G. Demostración: Como series de potencias, estas propiedades se cumplen en |z − a| < R para la parte regular y en |z − a| > r para la parte principal. Entonces se cumple en la intersección, r < |z − a| < R, para la serie de Laurent. 104 R r + a Figura 33: Corona circular de convergencia absoluta r < |z − a| < R (los bordes no están incluidos). Nota: Para una serie de Laurent siempre se supondrá r < R. Si r = 0 la corona de convergencia absoluta es el disco reducido de radio R, 0 < |z − a| < R. Si R = +∞ la corona es el exterior del disco de radio r, r < |z − a|. Si r = 0 y R = +∞, hay convergencia absoluta en todo C excepto quizá z = a. Teorema. Dada una serie de Laurent con suma s(z) en r < |z − a| < R, los coeficientes satisfacen Z s(z) 1 dz, n = 0, ±1, ±2, . . . (11.4) cn = 2πi γρ (z − a)n+1 siendo γρ una circunferencia (con orientación positiva) centrada en a de radio ρ, r < ρ < R. Demostración: 1 2πi Z γρ s(z) 1 dz = (z − a)n+1 2πi 1 = 2πi Z Z ∞ X γρ P∞ k=−∞ ck (z − (z − a)n+1 ∞ X γρ k=−∞ 1 = ck 2πi k=−∞ = cn . Z a)k dz ck (z − a)k−n−1 dz γρ (z − a)k−n−1 dz (11.5) Se ha R usado lanconvergencia uniforme para intercambiar suma e integral. En el último paso se usa que γρ (z − a) dz (n ∈ Z) es 2πi si n = −1 y 0 en otro caso. ♦ 105 Nótese que la integral no depende de ρ. Se deduce que los coeficientes son únicos en el sentido de que no hay dos series de Laurent con distintos coeficientes que den la misma suma. Definición. Si una función f (z) coincide con la suma de (11.3) en r < |z − a| < R se dice que admite desarrollo en serie de Laurent en esa corona circular. Ese desarrollo es único (en dicha corona) y ahı́ la función es analı́tica. El desarrollo de Laurent es una extensión del desarrollo de Taylor que puede aplicarse a funciones no analı́ticas en el punto en el que se desarrolla. ez Ejemplo. f (z) = no admite desarrollo en serie de Taylor en z = 0 pero sı́ admite desarrollo z de Laurent: 1 z2 z2 1 z z2 ez = (1 + z + + + ···) = + 1 + + + ··· , z z 2! 2! z 2! 3! 0 < |z| < +∞ . (11.6) Notablemente, las funciones que admiten desarrollo de Laurent no son excepcionales: Teorema. Si f (z) es analı́tica en la corona E = {ρ1 < |z −a| < ρ2 } entonces admite desarrollo de Laurent convergente en E, ∀z ∈ E ∞ X f (z) = n=−∞ cn (z − a)n . (11.7) Además, E está contenido en el dominio de convergencia de la serie de Laurent, es decir, si r y R denotan los radios de convergencia de la serie, se tiene r ≤ ρ1 < ρ2 ≤ R. Demostración: La última parte de la proposición, que E está contenido en el dominio de convergencia de la serie, se deduce de la primera parte ya que la serie converge en E. Si la proposición es cierta los coeficientes cn están totalmente fijados por (11.4). Entonces para z ∈ E, hay que demostrar que f (z) = f+ (z) + f− (z) con f+ (z) := ∞ X n=0 n cn (z − a) , f− (z) := ∞ X n=1 c−n 1 . (z − a)n (11.8) Sea ρ = |z − a| (ρ1 < ρ < ρ2 ). Para calcular cn usamos (11.4) integrando sobre una circunferencia 106 ζ z 0 C a r γρ γρ + R Figura 34: El camino γ, que empieza en ζ0 , recorre γρ+ , luego pasa por C, recorre γρ− en sentido horario y vuelve a pasar por C al revés, es cerrado y contenido en un dominio de analiticidad de la función f (ζ); la fórmula integral de Cauchy se aplica y produce f (z). (En la figura se ha tomado ρ1 = r y ρ2 = R.) de radio ρ+ con ρ < ρ+ < ρ2 , si n ≥ 0 y una circunferencia de radio ρ− con ρ1 < ρ− < ρ, si n < 0. Z ∞ X (z − a)n Z 1 f (ζ) f (ζ) dζ = dζ , f+ (z) = n+1 2πi (ζ − a) 2πi ζ − z γ γ ρ ρ + + n=0 Z Z ∞ X 1 1 f (ζ) 1 n−1 f (ζ)(ζ − a) dζ = − f− (z) = dζ . n (z − a) 2πi 2πi ζ − z γ γ ρ ρ − − n=1 (11.9) [Obsérvese que cn calculados integrando en (11.4), no dependen de los valores ρ± elegidos (siempre que ρ1 < ρ± < ρ2 ), pero ρ− < ρ < ρ+ garantiza que las series en (11.9) convergen absoluta y uniformemente, lo cual permite intercambiar suma con integral.] Si γ es el contorno que recorre γρ+ en sentido positivo y γρ− en sentido negativo, se deduce Z 1 f (ζ) f+ (z) + f− (z) = dζ = f (z) . (11.10) 2πi γ ζ − z La última igualdad es consecuencia de que γ equivale a un camino cerrado positivo contenido en un dominio de analiticidad simplemente conexo de f (z) y que encierra a z (véase la fig. 34). Esto demuestra la proposición. ♦ 107 Igual que para las series de Taylor también aquı́ se deduce que si f (z) admite desarrollo de Laurent centrada en z = a con radios de convergencia r y R, entonces, si r > 0 necesariamente f (z) debe tener al menos un punto singular en la circunferencia |z − a| = r, y si R < +∞ necesariamente f (z) debe tener al menos un punto singular en la circunferencia |z − a| = R. [De otro modo la corona de convergencia se podrı́a extender más allá de r < |z − a| < R.] Nota: Para una misma función f (z) y un mismo punto a, los coeficientes del desarrollo de Laurent de f (z) alrededor de a pueden cambiar al cambiar de corona circular. 1 es regular excepto en z = 0 y z = 1. Podemos considerar z(1 − z) dos desarrollos de Laurent centrados en z = 0: Ejemplo. La función f (z) = ∞ ∞ X 1X n z = zn. a) Corona 0 < |z| < 1. f (z) = z n=0 n=−1 1 b) Corona 1 < |z|. f (z) = − 2 z ∞ ∞ −2 X X 1 1 X 1 =− =− zn. =− 2 n n 1 z n=0 z z n=2 n=−∞ 1− z 1 1 (regular en z = 0) igualmente se pueden considerar desarrollos 1−z en la mismas coronas y los cn también son distintos en cada una. La diferencia con el caso f (z) = 1 1 es que para el desarrollo en la “corona” 0 < |z| < 1 no tiene parte principal z(1 − z) 1−z (potencia negativas) y de hecho vale en 0 ≤ |z| < 1. ♦ Obviamente, para la función Nótese que los desarrollos no siempre corresponden a |z − a| muy pequeño o muy grande. Por ejemplo, 1 1 1 1 z z2 z3 1 = + 2 + 3 + ··· + + 2 + 3 + 4 + ··· , (1 − z)(z − 2) z z z 2 2 2 2 1 < |z| < 2. (11.11) En este ejemplo la parte regular diverge is |z| > 2 y la principal diverge si |z| < 1. Teorema. (Desigualdades de Cauchy.) Si f (z) es analı́tica en una corona E = {ρ1 < |z − a| < ρ2 } y también acotada en E, |f (z)| ≤ K ∀z ∈ E, entonces |cn | ≤ K , ρn2 |c−n | ≤ Kρn1 , 108 n = 0, 1, 2, . . . (11.12) Demostración: Se aplica (11.4) integrando sobre la circunferencia de radio ρ, ρ1 < ρ < ρ2 , y mediante el teorema de la página 42 (Sec. ) se obtiene |cn | ≤ K ρn n = 0, ±1, ±2, . . . (11.13) Dado que este resultado vale para cada n para todo ρ entre ρ1 y ρ2 , se deduce el enunciado, que da la cotas óptimas. ♦ 11.2. Puntos singulares aislados Definición. Sea z0 ∈ C y sea f (z) analı́tica en 0 < |z −z0 | < R (para cierto R, 0 < R ≤ +∞) y no analı́tica en z0 . En este caso se dice que z0 es un punto singular aislado de f (z). Nótese que la función puede o no estar definida en z = z0 . ez Ejemplo. Sea f (z) = . Numerador y denominador son funciones enteras. z = 0 es un sen z punto singular, ya que es un cero (simple) de sen z y es punto singular aislado porque la función es analı́tica en 0 < |z| < π. Ejemplo. z = 0 no es un punto singular aislado de log z porque es una función multivaluada. Tampoco lo es de Log z ya que en este caso todos los puntos z ≥ 0 son singulares. Tampoco z = 0 en la superficie de Riemann del logaritmo (no es el plano complejo). Los puntos de ramificación no son puntos singulares aislados. 1 . Los puntos finitos en los que se anula el denominador son sen(1/z) singulares, zn = 1/(πn) (n 6= 0). También es singular el punto lı́mite de éstos, z = 0 (ya que f (z) no es derivable en todos los puntos de ningún entorno de z = 0). Los puntos z = zn son puntos singulares aislados, z = 0 no es un punto singular aislado (es singular, pero no aislado). Ejemplo. Sea f (z) = Nótese que el conjunto formado por funciones que en z0 tienen a lo sumo una singularidad aislada es cerrado bajo suma, resta, multiplicación y división. En las condiciones de la definición anterior, la función f (z) admite un desarrollo de Laurent f (z) = ∞ X n=−∞ cn (z − z0 )n , 109 0 < |z − z0 | < R . (11.14) Esto permite clasificar los puntos singulares aislados en tres clases: a) No hay potencias negativas: cn = 0 ∀n < 0. Se denomina singularidad evitable. La función ∞ X f (z) , z 6= z0 n ϕ(z) = cn (z − z0 ) = (11.15) c0 , z = z0 n=0 es analı́tica en z = z0 y coincide con f (z) cuando z 6= z0 . Es decir, f (z) admite una definición (o redefinición) en z = z0 de modo que sea analı́tica. z z2 ez − 1 no está definida en z = 0 sin embargo f (z) = 1 + + + ··· Ejemplo. f (z) = z 2! 3! cuando z 6= 0 y es analı́tica si se define f (0) = 1. Se puede demostrar que la singularidad es evitable sii existe el lı́mz→z0 f (z) y éste es finito. b) Hay un número finito no nulo de potencias negativas: Para cierto m > 0 c−m 6= 0 y cn = 0 ∀n < −m. En este caso z0 es un polo de orden m de f (z). f (z) = m X n=1 ∞ X c−n + cn (z − z0 )n , (z − z0 )n n=0 c−m 6= 0 (m ≥ 1) . (11.16) El polo es simple si m = 1 y múltiple si m > 1. ∞ X (z − z0 )m f (z) , z 6= z0 n La función g(z) = cn−m (z−z0 ) = es analı́tica en |z−z0 | < R. c−m , z = z0 n=0 Como g(z0 ) 6= 0 g(z) = ∞. (11.17) lı́m f (z) = lı́m z→z0 z→z0 (z − z0 )m Se puede demostrar que la singularidad aislada es de tipo polo sii lı́mz→z0 f (z) existe y éste es ∞. 1 , z 6= z m (z − z0 ) 0 La función es analı́tica en z = z0 y este punto es un cero de = f (z) 0, g(z) z=z 0 orden m. Y viceversa, si una función h(z) es analı́tica y tiene un cero de orden m en z0 , 1/h(z) tiene un polo de orden m. [En efecto, h(z) = (z − z0 )m G(z) G(z) analı́tica y G(z0 ) 6= 0, entonces 1/G(z) también es analı́tica en z0 y por tanto 1/h(z) = (1/G(z))(1/(z − z0 )m ) tiene un polo de orden m.] ez 1 Ejemplo. f (z) = tiene un polo simple en z = 0 ya que = e−z sen z es entera sen z f (z) con un cero simple en 0. 110 c) Hay un número infinito de potencias negativas: Para todo m < 0 existe n < m tal que cn 6= 0. En este caso z0 es una singularidad esencial de f (z). 1 1 1 1 1 + ··· + + · · · , converge para todo z 6= 0. Ejemplo. f (z) = e1/z = 1 + + 2 z 2! z n! z n z 1 1 1 1 Ejemplo. f (z) = = + 2 + 3 · · · , (|z| > 1) tiene infinitas potencias 1 = 1+ z−1 z z z 1− z negativas, pero z = 0 no es una singularidad esencial de f (z), ya que este desarrollo no tiene lugar en el anillo 0 < |z| < R. (De hecho, z = 0 es un punto regular de f (z).) Por exclusión, una singularidad es esencial si el lı́mz→z0 f (z) no existe. [Si existiera serı́a, bien finito (evitable) o infinito (polo).] De hecho cuando z → z0 , f (z) se puede aproximar tanto como se desee a cualquier valor prefijado, finito o infinito: Teorema. (Teorema de Casorati-Weierstrass.) Sea z0 una singularidad esencial de f (z) y sea α ∈ C∗ entonces existe una sucesión zn con lı́mite z0 tal que lı́mn→∞ f (zn ) = α. Demostración: (Ver, por ejemplo, el libro de Silverman.) De hecho hay una afirmación más fuerte: Teorema. (Teorema de Picard.) Si z0 es una singularidad esencial de f (z), para cualquier α ∈ C (excepto a lo sumo un punto α0 además de ∞) existe una sucesión zn → z0 tal que f (zn ) = α. Ejemplo. Sea f (z) = e1/z para z 6= 0. La función tiene una singularidad esencial en z = 0. Para α = ∞ del teorema de Casorati-Weierstrass, tomamos zn = 1/n, e1/zn = en → ∞. Para α = 0, tomamos zn = −1/n, e1/zn = e−n → 0. Para α cualquiera excepto 0, ∞, elegimos z tal que e1/z = α, con solución z = zn = 1/( Log α + 2πin). Entonces zn → 0 y e1/zn = α por construcción. zn es la solución que existe por el teorema de Picard, siendo α = 0, ∞ los valores excluidos por el teorema. Si z0 es una singularidad esencial de f (z) también lo es de 1/f (z), ya que tampoco 1/f (z) tiene lı́mite en z0 . De lo visto sobre singularidades aisladas se deduce que cuando (i) f (z) es una función analı́tica en la corona 0 < |z − z0 | < R, (ii) f (z) no es idénticamente 0, y (iii) z0 no es una singularidad esencial, entonces, f (z) = (z − z0 )m g(z) donde m ∈ Z, g(z) es analı́tica en el disco |z − z0 | < R, y g(z0 ) 6= 0. m y g(z) son únicos. Podemos decir que f (z) es de clase (z − z0 )m . Cuando m > 0 z0 es un cero de orden m de f (z), y cuando m < 0, z0 es un polo de orden −m de f (z). Si f (z) y h(z) son funciones de clase (z − z0 )m y (z − z0 )n , respectivamente, entonces f (z)h(z) es de clase (z − z0 )m+n y f (z)/h(z) de clase (z − z0 )m−n . 111 Definición. Se dice que una función f (z) es meromorfa en un dominio G si es analı́tica en G salvo singularidades aisladas de tipo polo. Una función es meromorfa (sin explicitar el dominio) si lo es en C. El conjunto de funciones analı́ticas en un dominio es cerrado bajo derivación, suma, resta y multiplicación pero no división. El conjunto de funciones meromorfas es cerrado también respecto de la división (excluida la división por la función idénticamente cero). ϕ(z) , siendo ϕ(z) y ψ(z) analı́ticas en un dominio ψ(z) G (y ψ(z) no idénticamente cero en G) son meromorfas en G. En efecto, f (z) es analı́tica salvo en los ceros de ψ(z) (que son aislados). Si z0 es un cero de orden m de ψ(z) y ϕ(z0 ) 6= 0, z0 es un polo de orden m de f (z). Si z0 es un cero de orden n de ϕ(z), entonces, si n < m z0 es un polo de orden m − n de f (z), si n ≥ m z0 es una singularidad evitable: definiendo f (z0 ) = lı́mz→z0 f (z) la función es analı́tica en z0 . Si n > m, z0 es un cero de orden n − m de f (z). Por otro lado toda función meromorfa con un número finito de polos se puede escribir como el cociente de una función analı́tica dividida por un polinomio. En particular, las funciones del tipo f (z) = 11.3. Del cálculo de series de Laurent: En principio cada coeficiente se puede obtener usando (11.4), pero esto no es práctico en general para obtener expresiones explı́citas (una fórmula). A diferencia de la serie de Taylor, no hay un algoritmo para obtener cada coeficiente de Laurent para funciones generales. Ejemplo. f (z) = ez+1/z alrededor de z = 0. ez admite desarrollo calculable en potencias de z y e1/z en potencias de 1/z, pero al multiplicarlas, el coeficiente de z n recibe infinitas contribuciones. ∞ X 1 . ♦ Por ejemplo c0 = (n!)2 n=0 Esencialmente en los casos en los que se puede obtener una expresión explı́cita es por reducción al caso de una singularidad aislada más cálculo de serie de Taylor. cos(z) , en |z| < π. Tiene un polo triple en z = 0. La función g(z) = z 3 f (z) 3 sen (z) tiene una singularidad evitable en z = 0, por tanto admite desarrollo en serie de Taylor. El desarrollo de Laurent de f (z) dividiendo el desarrollo de g(z) por z 3 . ♦ Ejemplo. f (z) = 112 1 en |z| > 1. Haciendo el cambio w = 1/z, la función auxiliar Ejemplo. f (z) = z log 1 + z 1 g(w) = 2 log(1 + w) tiene un polo simple en w = 0. Como antes, se puede cancelar el polo y w desarrollar en serie de Taylor en w. El desarrollo de Laurent original se obtiene deshaciendo el cambio de variable. ♦ 2 11.4. Residuos Definición. Sea z0 un punto singular aislado de f (z), f (z) = ∞ X n=−∞ cn (z − z0 )n , 0 < |z − z0 | < R . (11.18) El coeficiente c−1 se denomina el residuo de f (z) en z0 y se denota Res f (z). De acuerdo con z=z0 (11.4) para n = −1: Res f (z) = c−1 z=z0 1 = 2πi Z f (z) dz , (11.19) γρ siendo γρ una circunferencia orientada positivamente, de centro z0 y radio ρ < R. Nota: c−1 sólo es el residuo de f (z) en z0 para el desarrollo referido a 0 < |z − z0 | < R, no el coeficiente c−1 correspondiente a otras coronas circulares. Teorema. (Teorema de los residuos.) Sea C una curva cerrada, simple, suave a trozos y orientada positivamente. Sea f (z) analı́tica sobre C y también en su interior salvo por un conjunto finito de puntos singulares aislados (interiores a C), z1 , . . . , zn .46 Entonces Z n X f (z) dz = 2πi Res f (z) . (11.20) C k=1 z=zk Demostración: Para cada uno de los puntos singulares zk sea γk una circunferencia orientada positivamente centrada en zk , tal que esté contenida en el interior de C y que no rodee ningún otro punto singular. Entonces, Z n Z n X X f (z) dz = f (z) dz = 2πi Res f (z) . (11.21) C k=1 γk k=1 46 z=zk En realidad, dado que C define una región cerrada acotada el hecho de que las singularidades sean aisladas automáticamente garantiza que hay un número finito de ellas. 113 La primera igualdad usa la propiedad (5.20) (véase Sec ). La segunda, igualdad usa (11.19). ♦ Z ez dz, n ∈ Z mediante el teorema de residuos. Ejemplo. Cálculo de I = n |z|=2 (z − 1) Solución: Si n ≤ 0 no hay ningún punto singular sobre la circunferencia o su interior y la integral se anula. Si n > 0 la única singularidad del integrando es un polo de orden n en z = 1 ez que está rodeada por la circunferencia. Por el teorema de los residuos I = 2πi Res . Para z=1 (z − 1)n calcular el residuo desarrollamos el integrando en serie de Laurent (z − 1)2 e e (z − 1)k ez z−1 1 + (z − 1) + = e = + ··· + + ··· . (z − 1)n (z − 1)n (z − 1)n 2! k! (11.22) e El coeficiente c−1 corresponde a k = n − 1: c−1 = (n − 1)! 2πie , n = 1, 2, 3, . . . (11.23) I = (n − 1)! 0, n = 0, −1, −2, . . . ♦ 11.4.1. Cálculo de residuos Si la singularidad es evitable el residuo se anula. Si la singularidad es esencial debe calcularse el desarrollo en serie de Laurent. Queda el caso de una singularidad tipo polo. a) Polo de orden m. Sea z = z0 un polo de orden m de f (z): c−m c−1 f (z) = + ··· + + c0 + c1 (z − z0 ) + · · · , m (z − z0 ) z − z0 c−m 6= 0 . (11.24) Por tanto la función (z − z0 )m f (z) = c−m + · · · + c−1 (z − z0 )m−1 + c0 (z − z0 )m + · · · (11.25) es analı́tica. Se obtiene entonces la regla Res f (z) = “ (m − 1)-ésimo coeficiente de Taylor de (z − z0 )m f (z) en z = z0 ”. (11.26) z=z0 En particular, se puede usar la fórmula Res f (z) = lı́m z=z0 z→z0 dm−1 1 (z − z0 )m f (z) . m−1 (m − 1)! dz 114 (11.27) (Recuérdese, sin embargo, que derivar m − 1 veces no siempre es lo más eficiente para obtener el coeficiente de Taylor.) b) Polo simple. En este caso m = 1 y (11.27) implica Res f (z) = lı́m (z − z0 )f (z) . z=z0 z→z0 (11.28) Si f (z) = g(z)h(z) donde el polo lo lleva h(z), el cálculo del residuo se puede simplificar usando la propiedad Res f (z) = g(z0 ) Res h(z) z=z0 z=z0 (polo simple) (11.29) que es consecuencia inmediata de (11.28). La misma propiedad no se aplica en el caso de polos múltiples. ϕ(z) Si f (z) = donde ϕ(z), ψ(z) son analı́ticas en z = z0 y ψ(z) tiene un cero simple en z0 ψ(z) (por tanto ψ ′ (z0 ) 6= 0), entonces Res f (z) = lı́m ϕ(z) z=z0 z→z0 ϕ(z0 ) (z − z0 ) = ′ , ψ(z) ψ (z0 ) (11.30) donde se ha aplicado la regla de L’Hôpital (véase Sec. ). cos z en z = πn ∈ Z. Los ceros de sen z son simples y sen z cos z no se anula en ellos, por tanto se trata de polos simples y se aplica (11.30): cos z cos z = 1. ♦ (11.31) = Res z=πn sen z cos z z=πn Ejemplo. Residuo de f (z) = cotg z = 11.4.2. Residuo en el punto del infinito Sea E un subconjunto acotado de C, y sea f (z) analı́tica en C − E. Entonces, para un z0 ∈ C cualquiera puede tomarse R suficientemente grande de modo que E ⊂ {|z − z0 | < R} y f (z) será analı́tica en R < |z − z0 | < ∞. Sea f (z) = ∞ X n=−∞ cn (z − z0 )n , 115 R < |z − z0 | < ∞ (11.32) el desarrollo de Laurent asociado. Se define el residuo de f (z) en z = ∞ Res f (z) = −c−1 . (11.33) z=∞ (Obsérvese el signo menos en la definición.) Usando la fórmula general (11.4) Z 1 f (z) dz , Res f (z) = −c−1 = − z=∞ 2πi γρ (11.34) siendo γρ una circunferencia orientada positivamente, de radio ρ > R y centro z0 . La relación (11.34) demuestra que Res f (z) no depende en realidad del punto z0 usado para z=∞ hacer el desarrollo de Laurent (ya que la integral sobre otra circunferencia grande centrada en otro punto dará el mismo resultado) y sólo depende de la función. A menudo Res f (z) se obtiene z=∞ eligiendo z0 = 0. Teorema. Si f (z) es analı́tica en todo C excepto en un número finito de singularidades aisladas, z1 , . . . , zN , se cumple N X Res f (z) + (11.35) Res f (z) = 0 . z=∞ n=1 z=zn Demostración: Usando (11.34) y el teorema de los residuos 1 − Res f (z) = z=∞ 2πi 11.4.3. Z f (z) dz = γρ N X n=1 Res f (z) . ♦ z=zn (11.36) Cálculo del residuo en el infinito Elegimos z0 cualquiera (tı́picamente z0 = 0). Entonces c−1 c−m + ··· + + c0 + · · · + cn (z − z0 )n + · · · , R < |z − z0 | < ∞ m (z − z0 ) z − z0 1 cn (11.37) = · · · + c−m ζ m + · · · + c−1 ζ + c0 + · · · + n + · · · , 0 < |ζ| < , ζ R f (z) = · · · + donde se ha hecho el cambio de variable ζ = 1/(z − z0 ) (por tanto z = z0 + ζ −1 ). Esto implica 1 c−1 c0 cn −1 m−2 f (z + ζ ) = · · · + c ζ + · · · + c + + + · · · + + ··· , 0 −m −2 ζ2 ζ ζ2 ζ n+2 116 0 < |ζ| < 1 . R De aquı́ se deduce Res f (z) = − Res z=∞ ζ=0 1 f (z0 + ζ −1 ) . ζ2 (11.38) Y la expresión a la derecha es en realidad independiente de z0 . Nota: Alternativamente, 1 Res f (z) = − z=∞ 2πi Z 1 f (z) dz = − 2πi γρ 1 = − 2πi Z 1 dζ f (z0 + ζ −1 ) 2 = − Res 2 f (z0 + ζ −1 ) . ♦ ζ=0 ζ ζ γρ−1 Z γ −−1 f (z0 + ζ ρ −1 dζ ) − 2 ζ (11.39) z . Esta función es meromorfa con un polo simple en z = −1. El z+1 desarrollo de Laurent en torno a z = 0 produce Ejemplo. Sea f (z) = f (z) = 1 1 1 z = = 1 − + 2 − ··· , z+1 1 + 1/z z z 1 < |z| < ∞ . (11.40) se obtiene c−1 = −1 y Res f (z) = 1. Si hacemos el desarrollo en torno a z = −1 resulta z=∞ f (z) = 1 z =1− , z+1 z+1 0 < |z + 1| < ∞ . (11.41) (el desarrollo de Laurent tiene un número finito de términos). Los coeficientes cn han cambiado, excepto c−1 . Se obtiene el mismo residuo en ∞. Por otro lado Res f (z) = −1. Se verifica entonces z=−1 que la suma de todos los residuos, incluido el residuo en el infinito, se anula. Finalmente (eligiendo 1 1 1 1 1 1 z0 = 0), 2 f (ζ −1 ) = 2 = 2 − + O(1), y por tanto, − Res 2 f (ζ −1 ) = 1. ♦ ζ=0 ζ ζ ζ ζ +1 ζ ζ 117 12. 12.1. Aplicación del teorema de los residuos y otros resultados generales Evaluación de integrales impropias En la Sec. se definió la integral (de Riemann) sobre una curva suave a trozos. Como se vio allı́ esta integral se podı́a cambiar por una integral sobre un parámetro real t. Por tanto sin pérdida de generalidad discutimos el caso de integral en R. Rb Definición. La integral de Riemann a f (x) dx (f (x) real o compleja y −∞ < a ≤ b < ∞) se define como un lı́mite. Se dice que la integral existe o converge si este lı́mite existe y es finito. En este caso f (x) es integrable Riemann en [a, b]. Si f (x) es continua en [a, b] la integral existe. En cambio si sólo es continua en ]a, b[ la integral puede no existir ya que f (x) podrı́a tender a ∞ cuando x tiende a a o b, o esos lı́mites podrı́an no existir. Si el lı́mite que define la integral de Riemann no existe como tal o no es finito, pero sı́ lo hace tomándolo de cierta forma particular, a concretar, se dice que la integral es impropia. También es impropia si al menos uno de los lı́mites de integración es infinito. El caso más general que consideramos es I= Z +∞ f (x) dx (12.1) −∞ (Si la integral es en realidad sobre A ⊂ R basta definir f (x) = 0 para x 6∈ A.) Y sea f (x) continua en R salvo por un número finito de puntos, xk , k = 1, . . . , n en los que el lı́mite de f (x) cuando x → xk por la derecha o por la izquierda no existe o no es finito. En este caso I se define como el lı́mite de la integral regulada Z R2 Z xk+1 −ǫk+1 Z x1 −ǫ1 Z x2 −ǫ2 f (x) dx (12.2) +··· + + IR = +··· + −R1 x1 +ǫ′1 I := lı́m IR xk +ǫ′k xn +ǫ′n cuando R1,2 → +∞, ǫk , ǫ′k → 0+ . (12.3) Por definición, la integral impropia existe o converge si el lı́mite, al quitar los reguladores, existe y es finito. El lı́mite debe existir independientemente de cómo se quiten los reguladores. (Es decir, los lı́mites son todos independientes entre sı́). Si hay infinitos puntos xk (12.2) es una serie que también ha de converger independientemente. Si el lı́mite existe pero es infinito se dice que la integral es propiamente divergente. Si el lı́mite no existe se dice que la integral es indeterminada. 118 1 Ejemplo. f (x) = 2 . Cuando 0 < a < b < +∞, x Z Z R Z a 1 b 1 1 f (x) dx = − . Entonces a Zb 1 f (x) dx = 1 es convergente, en cambio f (x) dx = lı́m+ R→+∞ 1 ǫ→0 0 Z +∞ Z 1 piamente divergente, igual que f (x) dx ó f (x) dx. lı́m 0 Ejemplo. Z 1 −1 Z +∞ f (x) dx = 1 f (x) dx = +∞ es pro- ǫ −1 1 dx. El integrando diverge en x = 0. La integral regulada es x IR = Z −ǫ −1 1 dx + x Z 1 ǫ′ 1 dx = − x Z 1 ǫ 1 dx + x Z 1 ǫ′ 1 dx = log ǫ − log ǫ′ x (12.4) La integral impropia es indeterminada ya que el lı́mite no existe (es de tipo ∞ − ∞). De hecho puede obtenerse cualquier valor real incluido ±∞ tomando ǫ → 0+ manteniendo ǫ′ /ǫ constante. ♦ Z 1 1 √ dx. El integrando diverge en x = 0. La integral regulada es Ejemplo. x 0 Z 1 √ 1 √ 1 √ dx = 2 x = 2(1 − ǫ) −→ 2 . IR = (12.5) ǫ→0+ x ǫ ǫ La integral impropia es convergente. ♦ Algunas propiedades de la definición son Z c Z b Z c f (x) dx, si estas integrales f (x) dx+ f (x) dx = a) Si a < b < c (a, c finitos o infinitos) a a b existen. Además las integrales de la derecha convergen sii converge la de la izquierda. Z +∞ Z +∞ f (x − a) dx, si la integral existe. f (x) dx = b) −∞ −∞ c) Si existe, la integral es invariante bajo cambios de variable, y = y(x), dy/dx > 0. Teorema. Si la integral impropia converge absolutamente entonces converge. En particular, si la integral regulada de |f (x)| admite una cota independiente de los reguladores la integral de f (x) existe. 119 Definición. Se dice que f (x) = O(xα ) cuando x → 0 (α real) si |f (x)| < K|x|α para algún K > 0 en un entorno reducido de x = 0. Se dice que f (x) = O(xα ) cuando x → ±∞ (α real) si |f (x)| < K|x|α para algún K > 0 en un entorno de x = ±∞. Se deduce entonces a) Z Si f (x) es continua en ]0, a] y f (x) = O(xα ) cuando x → 0 para α > −1, la integral a f (x) dx existe. [Obsérvese que no basta lı́mx→0+ (xf (x)) = 0.47 ] 0 b) Z Si f (x) es continua en [a, +∞[ y f (x) = O(xα ) cuando x → +∞ para α < −1, la integral +∞ f (x) dx existe. [No es suficiente lı́mx→+∞ (xf (x)) = 0.] a Ejemplo. Para f (x) continua enZ x ≥ a ≥ 1 y con lı́mite finito en x = +∞, estúdiese la +∞ xα (log x)β f (x) dx. convergencia de la integral I(α, β) = a Solución: Hagamos el cambio de variable x = et , (dx = et dt) Z +∞ e(α+1)t tβ f (et ) dt . I(α, β) = (12.6) log a La convergencia está dominada por la exponencial. Si α + 1 > 0 la integral diverge (la exponencial tiende a +∞ cuando x → +∞), si α + 1 < 0 la integral converge (la exponencial tiende a 0). Si α + 1 = 0 la convergencia pasa a estar dominada por la potencia. De hecho la integral en t es del tipo I(β, 0) y por tanto converge sii β < −1. ♦ Para f (x) continua en [0, a] y f (0) 6= 0, estudiar la convergencia de la integral ZEjemplo. a I= xα | log x|β f (x) dx. 0 Solución: Haciendo de nuevo el cambio de variable x = et Z log a e(α+1)t |t|β f (et ) dt . I= (12.7) −∞ La integral converge si α+1 > 0 (la exponencial tiende a cero en t = −∞) y diverge is α+1 < 0. Si α + 1 = 0 estamos en un caso análogo al ejemplo anterior y la integral converge sii β > −1. ♦ 47 Por ejemplo, Ra 0 1/(x log x) dx no converge en x = 0. 120 12.1.1. de Valor principal de Cauchy Sea a < b < c y f (x) divergente en x = b. Se define, el valor principal de Cauchy R Definición. c f (x) dx como a P Z c a f (x) dx := lı́m+ ǫ→0 También se define P Z Z b−ǫ f (x) dx + a +∞ f (x) dx := lı́m R→+∞ −∞ Z Z c f (x) dx . b+ǫ R f (x) dx . −R (12.8) (12.9) Es decir, el valor principal de Cauchy corresponde a regular la integral como en (12.2) pero con R1 = R2 , ǫ′k = ǫk , y tomar el lı́mite. ♦ Evidentemente si la integral impropia converge también lo hace su valor principal de Cauchy, sin embargo hay casos en los que la integral no converge pero sı́ admite un valor principal de Cauchy. Z 2 dx no converge, en cambio Ejemplo. −1 x Z −ǫ Z 2 Z 2 Z 2 1 1 1 1 P dx = lı́m+ dx + dx = dx = log 2. (12.10) ǫ→0 −1 x ǫ x 1 x −1 x Donde se ha usado Z −ǫ −1 1 dx + x Z 1 ǫ 1 dx = 0 cuando ǫ > 0. ♦ x Algunas propiedades de la definición son Ra a) Si f (x) = −f (−x) (f (x) es impar) P −a f (x) = 0, donde a puede ser finito o infinito. R +∞ R +∞ b) En general P −∞ f (x) dx y P −∞ f (x − a) dx no coinciden. Rb c) Cuando existe, P a f (x) dx es invariante bajo cambios de variable (no singulares), si a, b son R +∞ finitos. [En general P −∞ f (x) dx no es invariante.] Ejemplo. Si f (x) es impar y lı́mx→+∞ f (x) → F , P 121 R +∞ −∞ f (x − a) dx = −2aF . 12.1.2. Integrales impropias en C Más generalmente si C es una curva suave z(t), a ≤ t ≤ b y f (z) es continua sobre C excepto z = z(b), Z Z b−ǫ dz (12.11) f (z) dz = lı́m+ f (z(t)) dt ǫ→0 dt C a (si existe el lı́mite y es finito). El caso general se obtiene juntando intervalos abiertos en los que función sea continua. Para caminos en el plano complejo, el valor principal de Cauchy se define al regular la integral excluyendo los puntos de C tapados por un disco Dǫ = {|z − z0 | < ǫ} y se toma el lı́mite ǫ → 0+ . Esta definición no depende de cómo se parametrice la curva. Si la discontinuidad de f (z) ocurre en z0 = z(t0 ), a < t0 < b, y t0 es un punto regular de z(t) esto equivale a Z t0 −ǫ Z b Z dz (12.12) f (z(t)) dt . + P f (z) dz = lı́m+ ǫ→0 dt t0 +ǫ a C 12.1.3. Lemas de integración Lema 1. Sea γR el arco de circunferencia z = Reiθ , θ1 ≤ θ ≤ θ2 . Si lı́mR→+∞ R|f (Reiθ )| = 0 Z para θ1 ≤ θ ≤ θ2 , entonces lı́m f (z) dz = 0. R→+∞ γR Demostración: El lı́mite implica que para R > R0 (ǫ),48 |f (Reiθ )| < ǫ/R . Entonces, Z ǫ (12.13) f (z) dz ≤ (θ2 − θ1 )R = ǫ(θ2 − θ1 ) −→ 0. ♦ R γR La proposición también se satisface si γR está centrado en otro punto z0 cualquiera. Lema 2. Sea γr el arco de Z circunferencia z = reiθ , θ1 ≤ θ ≤ θ2 . Si lı́mr→0+ r|f (reiθ )| = 0 f (z) dz = 0. La misma proposición vale si el arco está centrado para θ1 ≤ θ ≤ θ2 , entonces lı́m+ r→0 en otro punto z0 . γr Demostración: Análoga a la del Lema 1. 48 [θ1 , θ2 ] es cerrado y por tanto la convergencia es uniforme, de ahı́ que R0 no depende de θ 122 Lema 3. (Lema de Jordan.) Sea γR como en el Lema 1 pero contenido en el semiplano Im z ≥ 0, es decir, 0 ≤ θ1 < θ2 ≤ π. Si lı́mR→+∞ |f (Reiθ )| = 0 ∀θ ∈ [θ1 , θ2 ], entonces Z lı́m f (z)eiaz dz = 0 ∀a > 0. (12.14) R→+∞ γR Demostración: Z Z iaz f (z) e dz ≤ γR |f (z)| |e γR ≤ 2ǫR Z iaz | |dz| ≤ ǫR π/2 Z θ2 e−aR sen θ dθ θ1 e−aR sen θ dθ. (12.15) 0 Usando que sen θ ≥ 2θ/π para θ ∈ [0, π/2] (por ser sen θ una función convexa en ese intervalo) (véase la fig. 35.) 1 sen θ 2θ / π π/2 θ Figura 35: sen θ ≥ 2θ/π para θ ∈ [0, π/2]. Z γR f (z) e iaz Z dz ≤ 2ǫR π/2 e−2aRθ/π dθ = 2ǫR 0 1 − e−aR −→ 0. ♦ 2aR/π (12.16) De nuevo la proposición se satisface si el arco γR está centrado en otro punto, y también se puede adaptar a otros semiplanos, modificando la condición a > 0 correspondientemente.49 Nota: La condición lı́mR→+∞ |f (Reiθ )| = 0 se puede relajar considerablemente cuando 0 < θ1 < θ2 < π. En este caso, sea θm = mı́n(θ1 , π−θ2 ) y por hipótesis 0 < sen θm ≤ sen θ ∀θ ∈ [θ1 , θ2 ]. 49 Concretamente, si γR está en el semiplano θ ∈ [θ0 , θ0 + π] la proposición se cumple para todo a con arg a = −θ0 . 123 Entonces el lema se satisface suponiendo sólo que lı́mR→+∞ R|f (Reiθ )|e−aR sen θm = 0 ∀θ ∈ [θ1 , θ2 ]. Esto cubre los casos |f | < KRα (crecimiento tipo potencia), e incluso |f | < KeαR (crecimiento exponencial) si α < a sen θm . Lema 4. Sea z0 un polo simple de f (z) y sea γǫ el arco z = z0 + ǫ eiθ , θ1 ≤ θ ≤ θ2 , entonces Z lı́m+ f (z) dz = i(θ2 − θ1 ) Res f (z). (12.17) ǫ→0 z=z0 γǫ Dicho de otro modo, si el polo es simple, la integral es proporcional al ángulo subtendido (si la circunferencia es completa se obtiene 2πi veces el residuo, de acuerdo con el teorema de los residuos). La proporcionalidad no se mantiene si el polo es múltiple. c−1 + h(z) y h(z) es una función regular. Por z − z0 el Lema 2, la integral de la parte regular se anula en el lı́mite. La integral de la parte principal es inmediata y resulta la proposición. Demostración: Sea c−1 el residuo, f (z) = Nota: La proposición sólo se refiere a polos simples. Para polos múltiples se tiene el siguiente resultado. Sea γǫ el arco ǫeiθ , 0 ≤ θ ≤ π (una semicircunferencia). Entonces Z 1 +∞ n = 2, 4, 6, . . . dz = (12.18) lı́m+ n 0 n = 3, 5, 7, . . . ǫ→0 γǫ z 12.1.4. Integrales impropias γR ia IR −R Figura 36: Contorno para R∞ dx −∞ (x2 +a2 )3 124 R y R +∞ 0 cos x dx, x2 +a2 a > 0. Ejemplo 1. I= Z +∞ dx , + a2 ) 3 (x2 −∞ a > 0. (12.19) Esta integral converge ya que el integrando es O(x−6 ) cuando x → ±∞. 1 y CR la curva cerrada de la figura 36. CR está compuesta por el segmento + a2 ) 3 IR = [−R, R] y la semicircunferencia γR de radio R centrada en 0. El punto z = ia es un polo triple de f (z) y es el único punto singular contenido en C. Por el teorema de los residuos Z f (z) dz = 2πi Res f (z) . (12.20) Sea f (z) = (z 2 z=ia CR Res f (z) = z=ia 1 1 1 3×4 3 d2 (z − ia)3 d2 1 lı́m 2 2 = lı́m = = , 2 3 2 3 5 2! z→ia dz (z + a ) 2! z→ia dz (z + ia) 2 (2ia) 16ia5 Z 3π f (z) dz = 5 . 8a CR (12.21) (12.22) Esta integral no depende de R. Por otro lado I = lı́m R→+∞ Z Z f (z) dz = CR R f (x) dz = lı́m −R R→+∞ Z Z f (z) dz + IR f (z) dz = IR Z CR Z f (z) dz . f (z) dz − lı́m R→+∞ Para completar el cálculo falta ver que el último término se anula: Z lı́m f (z) dz = 0 . R→+∞ (12.23) γR Z f (z) dz . (12.24) γR (12.25) γR 1 En efecto, f (z) ∼ 6 y por tanto f (Reiθ ) = O(R−6 ) cuando R → +∞. El término se anula z→∞ z entonces por aplicación del Lema 1. Se obtiene finalmente I= 3π , 8a5 125 a > 0. (12.26) Notas: 1) Como debe ser, verifica I > 0. 2) El integrando sólo depende de a2 , por tanto la integral es invariante bajo a → −a. Eso no es manifiesto en el resultado final porque hemos elegido 3π . llamar a a la raı́z cuadrada positiva de a2 . Se puede prescindir de esta elección escribiendo I = 8|a|5 En el cálculo se ha usado a > 0 al decir que el polo en el semiplano superior es z = ia en vez de z = −ia. 3) CR está centrado en z = 0 pero se hubiera podido usar similar centrado en R +∞un contorno 2 2 −1 cualquier otro punto del eje real. 4) También se puede calcular −∞ (x + a ) dx y luego derivar dos veces respecto de a2 para obtener la integral pedida. Ejemplo 2. I= Z +∞ 0 cos x dx, x 2 + a2 a > 0. (12.27) El integrando es O(x−2 ) cuando x → ±∞ y la integral es convergente. La integral es real (y de hecho positiva). Para poder aplicar el Lema de Jordan (Lema 3) consideramos la integral Z +∞ eix ′ I = dx, a > 0 . 2 2 −∞ x + a (12.28) Esta integral está relacionada con la anterior mediante50 I= 1 Re I ′ , 2 (12.29) por Re eix = cos x y ser cos x una función par en x. eiz , y sea CR = IR ∪ γR la misma curva cerrada del Ejemplo 1, figura 36. La z 2 + a2 única singularidad de f (z) sobre o en el interior de CR es un polo simple en z = ia. Por tanto Z π (12.30) f (z) dz = 2πi Res f (z) = e−a . z=ia a CR Sea f (z) = Por otro lado ′ I = lı́m 50 R→+∞ Z R f (x) dz = lı́m −R R→+∞ Z f (z) dz = IR Z CR f (z) dz − lı́m R→+∞ Z f (z) dz . γR De hecho I = 12 I ′ ya que Im I ′ = 0 por Im eix = sen x y ser sen x una función impar de x. 126 (12.31) El último término se anula por aplicación del Lema de Jordan. Esto puede hacerse por f (Reiθ ) = O(R−2 ) cuando R → +∞ para 0 ≤ θ ≤ π. Obsérvese que el lema no se aplicarı́a a la función cos z eiz + e−iz = por el término con e−iz que crece exponencialmente en el semiplano Im z > 0. z 2 + a2 2(z 2 + a2 ) Se deduce I= π −a e , 2a a > 0. (12.32) Se verifica que el resultado es real. Obsérvese que para hacer la integral se ha extendido el intervalo de integración de ]0, +∞[. a ] − ∞, +∞[. En general la integrales basadas en teorema de residuos deben tener recorridos naturales. Como regla las integrales con lı́mites arbitrarios no pueden obtenerse mediante residuos. γR γ− ε −ε ε −R R Figura 37: Contorno para la integral Ejemplo 3. R +∞ 0 sen x x dx. +∞ sen x dx . (12.33) x 0 El integrando es O(1) cuando x → 0 y ahı́ no hay problema de convergencia, pero es O(1/x) cuando x → +∞ y ahı́ no está garantizada la convergencia. Como se verá del cálculo, la integral converge, es decir, el lı́mite Z R sen x dx (12.34) lı́m x ǫ ǫ→0+ I= Z R→+∞ existe y es finito. eiz , y el circuito C z γR y γǫ son semicirfunferencias centradas en Con vistas a aplicar el teorema de residuos, consideramos la función f (z) = de la figura 37. C = [−R, −ǫ] ∪ γǫ− ∪ [ǫ, R] ∪ γR . 127 z = 0 de radios R y ǫ, con orientación positiva (es decir, sentido antihorario). γǫ− es γǫ recorrido en sen z tiene una singularidad evitable en sentido negativo (horario). Obsérvese que la función original z z = 0 y para ella bastarı́a usar el contorno [−R, R], sin rodear z = 0 con el arco γǫ− . Sin embargo eiz , que tiene un polo simple en z = 0. para poder aplicar el Lema de Jordan hemos cambiado a z Puesto que f (z) es analı́tica sobre y en el interior de C Z f (z) dz = 0 . (12.35) C Por otro lado Z f (z) dz = C Z −ǫ + −R Z R + ǫ Z γR − Z f (z) dz . (12.36) γǫ La integral en la semicircunferencia del infinito se anula por aplicación del Lema de Jordan: Z lı́m f (z) dz = 0 . (12.37) R→+∞ γR Dado que el polo en z = 0 es simple, el Lema 4 es aplicable, y produce Z 1 lı́m+ f (z) dz = 2πi Res f (z) = iπ . z=0 ǫ→0 2 γǫ (12.38) Se deduce iπ = = lı́m+ lı́m ǫ→0 R→+∞ lı́m+ lı́m ǫ→0 R→+∞ Z Z −ǫ −R R ǫ + Z ǫ R eix dx = lı́m+ lı́m ǫ→0 R→+∞ x 2i sen x dx = 2iI , x es decir, I= Z R ǫ eix − e−ix dx x π . 2 (12.39) (12.40) Alternativamente, Z +∞ Z 1 +∞ sen x 1 sen x I = dx = P dx 2 −∞ x 2 −∞ x Z −ǫ Z R ix Z +∞ ix e 1 1 e = Im P dx = Im lı́m+ lı́m dx . + ǫ→0 R→+∞ 2 x 2 x −∞ ǫ −R 128 (12.41) La integral sobre [−R, −ǫ] ∪ [ǫ, R] puede entonces completarse con γǫ−Z y γR como antes y apli+∞ sen x dx, la integral car el teorema de residuos. Obsérvese que, a diferencia de la integral x 0 Z +∞ ix e dx no existe. (Existe si se añade alguna prescripción, tal como el valor principal de Cauchy.) x −∞ e iπ /4 R γ IR R R Figura 38: Contorno para las integrales de Fresnel, Ejemplo 4. (Integrales de Fresnel.) Z +∞ cos(x2 ) dx , I1 = I2 = 0 Z R +∞ 0 cos(x2 ) dx, R +∞ 0 sen(x2 ) dx. +∞ sen(x2 ) dx . (12.42) 0 2 Sea f (z) = eiz , y sea C el contorno representado en la figura 38. C = [0, R] ∪ γR ∪ IR− , siendo γR = {Reit , t ∈ [0, π/4]} IR = {teiπ/4 , t ∈ [0, R]}, (arco de radio R y 1/8 de vuelta), (siendo IR− el arco IR recorrido al revés). Dado que C no encierra ninguna singularidad Z R Z Z 0= f (z) dz = + C Claramente I1 + iI2 = 0 Z +∞ e ix2 γR − dx = lı́m Z R→+∞ 0 129 (12.43) (12.44) f (z) dz . (12.45) f (z) dz . (12.46) IR Z R 0 Por otro lado51 Z Z lı́m f (z) dz = lı́m R→+∞ R→+∞ IR Y finalmente lı́m R→+∞ Z e R e −t2 iπ/4 e dt = e 0 iz 2 dz = 2 lı́m w=z R→+∞ γR iπ/4 Z γR,w Z +∞ e −x2 dx = e iπ/4 0 √ π . 2 eiw dw −→ 0 , R→+∞ 2w1/2 (12.47) (12.48) donde γR,w = {R2 eit , t ∈ [0, π/2, ]} y se ha aplicado el Lema de Jordan. Reuniendo los resultados 0 = I1 + iI2 + 0 − e √ Usando eiπ/4 = (1 + i)/ 2, 1 I1 = I2 = 2 C3 r iπ/4 √ π . 2 π . 2 (12.50) 2πi C2 iπ C4 R C1 Figura 39: Contorno para la integral Ejemplo 5. I= 51 Usando Z Z +∞ 2 e−x dx = 2 e−x dx 0 √ 2 = Z Z +∞ −∞ eax dx, 1 + ex R +∞ −∞ eax /(1 + ex )dx. (0 < a < 1). (12.51) π . En efecto, 2 0 +∞ (12.49) +∞ dx 0 Z +∞ dy e−(x 2 +y 2 ) = 0 130 Z π/2 dθ 0 Z +∞ 2 drr e−r = 0 π 4 Z +∞ dξ e−ξ = 0 π . 4 La integral converge en +∞ por a < 1 y en −∞ por a > 0. En realidad la integral existe también para a complejo si 0 < Re a < 1. Sea f (z) = eaz /(1 + ez ) y sea C = C1 ∪ C2 ∪ C3− ∪ C4− el contorno representado en la figura 39. f (z) tiene polos simples en z = iπ(2n + 1), n ∈ Z. De éstos sólo z = iπ cae dentro de C. Z eaz (12.52) f (z) dz = 2πi Res f (z) = 2πi lı́m z = −2πieiπa . z=iπ z→iπ e C Veamos que las integrales a lo largo de C2 y C4 se anulan cuando R → +∞. Como estas integrales son sobre intervalos compactos es suficiente verificar que f (z) tiende a cero sobre ellos: aR iya (a−1)R e e = e z ∈ C2 |f (z)| = −→ 0 (por a < 1) , 1 + eR eiy |e−R−iy + 1| R→+∞ e−aR z ∈ C4 |f (z)| = −→ 0 (por a > 0) . (12.53) |1 + e−R+iy | R→+∞ La integral sobre C1 tiende a I, y por otro lado la integral sobre C3 puede relacionarse con esta Z Z R Z R ax 2πia Z e e 2πia f (z) dz . (12.54) dx = e f (z) dz = f (x + 2πi) dx = x C1 −R −R 1 + e C3 Se deduce −2πieiπa = I + 0 − e2πia I − 0 , y de ahı́ I = 2πi eiπa 2πi π = iπa = . 2πia −iπa e −1 e −e sen(πa) (12.55) (12.56) La integral es positiva cuando 0 < a < 1 y diverge cuando a tiende a los valores 0 o 1. Nota: Mediante un cambio de variable esta integral puede llevarse a una del tipo del Ejemplo 7. Ejemplo 6. I= Z +∞ 0 log x dx. (x2 + 1)2 (12.57) Debido a la presencia del logaritmo, el integrando no es O(x−4 ) cuando x → +∞ pero sı́ O(xα ) para cualquier α > −4 y la integral converge en +∞ (basta α < −1). Igualmente, el integrando es 131 γR i γ− ε −R −ε ε Figura 40: Contorno para la integral R R +∞ 0 log x/(x2 + 1)2 dx. O(xα ) cuando x → 0+ para cualquier α < 0, y la integral converge en x = 0. 52 log z , y sea C el contorno representado en la figura 40. f (z) tiene polos dobles (z 2 + 1)2 en z = ±i y puntos de ramificación en z = 0, ∞. Para el logaritmo elegimos la rama en la que log 1 = 0. Entonces por continuidad sobre el circuito C, log z es real cuando z es real y positivo, y log |z| + iπ cuando z es real y negativo. Esto es general cuando hay funciones multivaluadas: El circuito debe dejar fuera los puntos de ramificación. Una vez elegido el valor de la función en un punto del circuito, el valor de la función queda fijado por continuidad en todos los demás puntos del circuito y de su interior. En el presente caso el argumento de z para el logaritmo lo tomamos en [0, π]. Sea f (z) = Aplicamos el teorema de residuos a la integral de f (z) sobre C: a) Las integrales sobre γR y γǫ tienden a cero por aplicación inmediata de los Lemas 1 y 2. b) La integral sobre [ǫ, R] tiende a I. c) La integral sobre [−R, −ǫ] puede relacionarse con I: Z −ǫ Z −ǫ log z log |x| + iπ dz = dx −→ I + iπI1 , 2 2 2 2 −R (z + 1) −R (x + 1) R→+∞ (12.58) ǫ→0+ Como regla, un integrando que se comporte como xα logβ x cuando x = 0+ converge si (condición suficiente) α > −1. Y si se comporta como xα logβ x cuando x = +∞, converge si α < −1. Es decir, en ambos casos, si la potencia α es tal que la integral converge, el logaritmo no modifica esa situación. 52 132 donde I1 = Z +∞ (x2 0 1 dx . + 1)2 (12.59) d) La integral sobre todo C se obtiene por residuos. El único punto a tener en cuenta es que al calcular el residuo hay que usar la misma hoja de la función multivaluada que se ha usado sobre el circuito. En el presente caso, log i = iπ/2. Z d log z 1 log z = f (z) dz = Res 2 z=+i (z + 1)2 2πi C dz (z + i)2 z=i 1 log z i π = (12.60) −2 = + . 2 3 z(z + i) (z + i) z=i 4 8 En conjunto se obtiene 2πi i π + 4 8 = I + 0 + I + iπI1 + 0 (12.61) La integral I1 puede calcularse como en el Ejemplo 1. Sin embargo no es necesario. Teniendo en cuenta que I e I1 son reales, se deduce π π I = − , I1 = . (12.62) 4 4 +∞ xa−1 dx derivando 1 + x2 0 respecto de a. I ′ se obtiene por un método análogo al seguido en el Ejemplo 7. ′ Nota: Esta integral puede también obtenerse a partir de I = Ejemplo 7. I= Z +∞ 0 xa−1 dx, 1+x 0 < a < 1. Z (12.63) La integral converge en x = 0 para a > 0 y en x = +∞ para a < 1. Para aplicar el teorema de z a−1 y el contorno C de la figura 41. En este contorno, residuos consideramos la función f (z) = 1+z R → +∞, y r, ǫ → 0+ . La función tiene un polo simple en z = −1 y puntos de ramificación en z = 0, ∞. Para la función multivaluada elegimos la rama en la que z a−1 es un número real positivo cuando z es real y positivo (a es real). Por continuidad sobre el circuito y su interior esto equivale a tomar el argumento de z en el intervalo [0, 2π − ǫ]. Aplicamos el teorema de residuos a la integral de f (z) sobre C: 133 γ γr R C1 ε −1 C2 Figura 41: Contorno para la integral R +∞ 0 xa−1 /(1 + x) dx. a) Las integrales sobre γR y γr tienden a cero cuando R → +∞ y r → 0+ por aplicación inmediata de los Lemas 1 y 2 (usando 0 < a < 1). b) La integral sobre C1 = [r, R] tiende a I. c) La integral sobre C2 = {te−iǫ , r ≤ t ≤ R} puede relacionarse con I (en el lı́mite): Tal y como se ha elegido la rama de la potencia, z a−1 (t) = ta−1 ei(2π−ǫ)(a−1) . Entonces Z C2 z a−1 dz = 1+z Z R a−1 i(2π−ǫ)(a−1) t r e 1 + te−iǫ e−iǫ dt −→ e2πi(a−1) I = e2πia I, (12.64) d) La integral sobre todo C se obtiene por residuos, teniendo en cuenta que hay que tomar arg(−1) = π: Z 1 z a−1 = z a−1 f (z) dz = Res = eiπ(a−1) = −eiπa . (12.65) z=−1 1 + z 2πi C z=−1 En conjunto, I=− −2πieiπa = I + 0 − e2πia I − 0. (12.66) 2πi π 2πieiπa . = − = 1 − e2πia e−iπa − eπia sen(πa) (12.67) 134 Como debe ser, el resultado es positivo cuando 0 < a < 1, y diverge cuando el parámetro a se acerca a los lı́mites del intervalo. (Fuera del intervalo ]0, 1[, aunque el resultado sea finito, ya no se corresponde con la integral, que no existe, y de hecho no es definido positivo.) Notas: 1) En la práctica se suele poner directamente ǫ = 0, de modo que C1 y C2 son el mismo intervalo [r, R] en el plano complejo (pero distintos en la superficie de Riemann) y la función toma distintos valores sobre C1 y C2 . 2) Las integrales del tipo del Ejemplo 5 se pueden reducir a la del presente ejemplo con el cambio de variable x = log y. 3) Las integrales del tipo del EjemploZ6 pueden relacionarse conZlas del presente ejemplo: Sea R(x) una función racional y sea +∞ +∞ dn I(a) a . xa logn x R(x) dx = x R(x) dx, entonces I(a) = dan 0 0 γ R i γ r R Figura 42: Contorno para la integral P Ejemplo 8. I=P R 1 Z +∞ −∞ R +∞ −∞ ((x − 1)(x2 + 1))−1 dx. dx (x − 1)(x2 + 1) (12.68) La integral converge en x = ±∞. El integrando tiene un polo simple en x = 1, por lo que la integral no existe, pero sı́ admite un valor principal de Cauchy, que es el que se pide. Para aplicar el teorema de residuos se puede usar el contorno C representado en la figura 42. Este contorno rodea el polo en el camino de integración dejándolo fuera. Aparte, la extensión analı́tica del integrando, f (z) = 1/((z − 1)(z 2 + 1)), tiene polos simples adicionales en z = ±i. a) La integral sobre [−R, 1 − r] ∪ [1 + r, R] (es decir la parte del contorno que sigue el eje real) tiende a I, cuando R → +∞ y r → 0+ . b) La integral sobre γR tiende a 0 cuando R → +∞ por aplicación del Lema 1. 135 c) La integral sobre γr no tiende a 0. Como z = 1 es un polo simple se puede aplicar el Lema 4. Z 1 1 iπ lı́m+ dz = iπ Res = . (12.69) 2 2 z=1 (z − 1)(z + 1) r→0 2 γr (z − 1)(z + 1) b) La integral sobre todo el contorno completo se obtiene por residuos, teniendo en cuenta que z = i es la única singularidad contenida en C. Z π 1 1 dz = 2πi Res = − (1 + i). (12.70) 2 2 z=i (z − 1)(z + 1) 2 C (z − 1)(z + 1) En conjunto iπ π + 0. − (1 + i) = I − 2 2 π I=− . 2 (12.71) (12.72) La integral es real. Nota: Igualmente se hubiera podido elegir C de modo que γr rodeara el polo z = 1 por debajo, incluyéndolo en su interior. En este caso la integral sobre γr se sumarı́a a la derecha de (12.71) en vez de restarse, pero también habrı́a que añadir 2πi veces el residuo de ese polo a la izquierda de la ecuación (ya que ahora está dentro de C), y por supuesto se obtiene el mismo resultado. Como regla práctica, en el cálculo de la parte principal de Cauchy mediante el teorema de residuos, lo más cómodo es rodear los polos dejándolos fuera del contorno. Ejemplo 9. I=P Z +∞ 0 xα−1 dx, x−a a > 0, 0 < α < 1. (12.73) La convergencia en x = 0 está garantizada por α > 0, y en x = +∞ por α < 1. El integrando es singular en x = a (en el camino de integración) y nos piden la parte principal de Cauchy. z α−1 . Esta función tiene un z−a polo simple en z = a y puntos de ramificación en z = 0, ∞. La integral se hará sobre el contorno C mostrado en la figura 43. El contorno excluye los puntos singulares. Para la potencia z α−1 en f (z) elegimos arg z ∈]0, 2π[ en el interior de C. En I1 arg z = 0 y en I2 arg z = 2π. Para aplicar el teorema de residuos consideramos la función f (z) = a) La integral sobre todo C es cero ya que no encierra ninguna singularidad. 136 γ γ r γ1 a γ R R I1 R I 2 2 Figura 43: Contorno para la integral P R +∞ 0 xα−1 x−a dx. b) La integral sobre γR tiende a cero por aplicación del Lema 1. La integral sobre γr tiende a cero por aplicación del Lema 2. c) Sobre I1 = [r, a − r] ∪ [a + r, R], (alcanzado desde Im z > 0) f (z) = Por tanto, Z I1 f (z) dz −→ I. d) Sobre I2 = [r, a − r] ∪ [a + r, R], (alcanzado desde Im z < 0) f (z) = z = t). Por tanto, Z I2 f (z) dz −→ e2πi(α−1) I = e2πiα I. tα−1 (para z = t). t−a (12.74) tα−1 e2πi(α−1) (para t−a (12.75) e) Dado que el polo en z = a es simple, las integrales sobre las semicircunferencias γ1 y γ2 se pueden obtener por aplicación del Lema 4. El único punto a tener en cuenta es que en γ1 arg z = 0 y en γ2 arg z = 2π. Z f (z) dz −→ iπ Res f (z)arg z=0 = iπaα−1 . z=a Zγ1 f (z) dz −→ iπ Res f (z)arg z=2π = iπaα−1 e2πi(α−1) = iπaα−1 e2πiα . (12.76) γ2 z=a 137 En conjunto 0 = I + 0 − e2πiα I − 0 − iπaα−1 − iπaα−1 e2πiα . (12.77) 2πiα I = iπ 1+e aα−1 = −π cotg(πα)aα−1 . 2πiα 1−e (12.78) C R C I1 a I2 b Figura 44: Contornos para la integral Ejemplo 10. I= Z b a 1 p (x − a)(b − x) Rb a 1/ dx, p (x − a)(b − x) dx. a < b. (12.79) El integrando es singular en x = a, b sin embargo son singularidades de orden O(x−1/2 ) y por tanto integrables. También se observa que en realidad I no depende de a, b (siempre que a < b). Haciendo un cambio de variable se puede elegir a = 0 y b = 1 sin cambiar el valor de la integral. Para aplicar el teorema de residuos consideramos la función f (z) = √ 1 √ , z−a z−b donde √ i z := |z|e 2 Arg z , Arg z ∈ [0, 2π[ (12.80) Tal y como está definida, la función f (z) tiene un valor finito en todos los puntos excepto z = a y z = b y es analı́tica en todo el plano complejo excepto el intervalo [a, b]. Sobre este intervalo la función tiene una discontinuidad. En su superficie de Riemann a y b son puntos de ramificación pero en cambio ∞ no es de ramificación (después de una vuelta completa alrededor de un contorno que contenga a y b se vuelve al mismo valor). 138 Sea C el contorno mostrado en la figura 44. a) Las integrales sobre las pequeñas circunferencias centradas en a y b tienden a cero (Lema 2). + b) I1 = [a + ǫ, b − ǫ] √(alcanzado √ z > 0). Para √ z ∈ I1 , z = x + i0 , Arg (z − a) = 0, √desde Im Arg (z − b) = π, z − a = x − a, z − b = i b − x. Se deduce Z i √ , f (z) dz −→+ −iI. (12.81) z ∈ I1 , f (z) = − √ ǫ→0 x−a b−x I1 + c) I2 = [a + ǫ, b − ǫ] √ (alcanzado desde Im √ z < 0). Para √ z ∈ I2 , z = x − i0 , Arg (z − a) = 2π, √ Arg (z − b) = π, z − a = − x − a, z − b = i b − x. Se deduce Z i √ , f (z) dz −→+ iI. (12.82) z ∈ I2 , f (z) = √ ǫ→0 x−a b−x I2 En conjunto (la integral sobre C no depende de ǫ) Z f (z) dz = 2iI. (12.83) C d) Como ∞ no es un punto de ramificación la integral se puede obtener aplicando el teorema de residuos calculando el residuo en el infinito (la integral sobre C es la misma que sobre CR y sólo se necesita f (z) para |z| = R muy grande): Z Z f (z) dz = f (z) dz = −2πi Res f (z). (12.84) C CR f (z) = √ z=∞ 1 1 1 √ = + O( 2 ). z z z−a z−b (12.85) (f (z) está definida de modo que tiende a 1/z cuando z → ∞, y no a −1/z, como es fácil de verificar.) Se deduce Res f (z) = −1. z=∞ Finalmente I = π. El resultado verifica que es positivo y no depende de a, b (para a < b). 139 (12.86) Notas: 1) En este tipo de integrales (el intervalo de integración une dos puntos de ramificación) conviene definir f (z) de modo que tenga el corte de rama √ sobre el√intervalo de integración. √ √ Ası́ 1/( z − a z − b) cumple esa propiedad, mientras que 1/( z − a b − z) tiene el corte de rama en ] − ∞, a] ∪ [b, +∞[. 2) Como es fácil perderse en la superficie de Riemann de una función multivaluada, conviene trabajar con √ funciones multivaluadas elementales cuyas propiedades se conozcan bien (en el presente Ejemplo z definida en (12.80)) aunque sea a costa p de trabajar con una función no idéntica al√integrando (en el presente Ejemplo el integrando es 1/( (x − a)(b − x)) √ pero f (z) = 1/( z − a z − b)). Es decir, es mejor adaptar f (z) a las funciones multivaluadas involucradas que adaptar la función multivaluada al integrando. 12.2. Suma de series Sean π π , F− (z) := . (12.87) tan(πz) sen(πz) Estas funciones tienen polos simples en z = n ∈ Z con residuos (±1)n respectivamente. Además son periódicas. Estas propiedades hacen que se puedan utilizar para sumar series: F+ (z) := Teorema. Sea f (z) analı́tica en C salvo un número finito de singularidades aisladas zk 6∈ Z, k = 1, . . . , N , y tal que zf (z) → 0 cuando z → ∞. Entonces +∞ X n=−∞ n (±1) f (n) = − N X k=1 Res F± (z)f (z) . z=zk (12.88) Demostración: (Cualitativa) Basta considerar un contorno grande Cn , por ejemplo el cuadrado paralelo a los ejes y centrado en cero, que corte el Reje real en z = n + 1/2 (que evita los polos de F± (z)). En el lı́mite de contorno grande la integral Cn F± (z)f (z) dz se anula (F± (z) está acotada sobre Cn y f (z) tiende a cero suficientemente deprisa). Una aplicación del teorema de residuos produce inmediatamente la proposición ya que las singularidades de F± (z) están en z = n ∈ Z y las de f (z) en zk , k = 1, . . . , N . ♦ ∞ X (−1)n Ejemplo. Calcúlese la suma . n2 + a2 n=1 +∞ X 1 (−1)n . Tomando f (z) = 2 , que tiene polos en Solución: Consideramos primero 2 2 2 n + a z + a n=−∞ 140 z = ±ia, el teorema implica +∞ X π F− (z) F− (z) 1 (−1)n = − Res 2 − Res 2 = . 2 2 2 2 z=ia z + a z=−ia z + a n +a a senh(πa) n=−∞ Por otro lado (12.89) +∞ ∞ X X (−1)n 1 (−1)n = + 2 , implica 2 + a2 2 2 + a2 n a n n=−∞ n=1 ∞ X π 1 1 (−1)n = − . n2 + a2 2a senh(πa) 2a2 n=1 (12.90) ♦ 12.3. Residuo logarı́tmico y principio de variación del argumento Definición. Sea f (z) analı́tica en 0 < |z−z0 | < R y no idénticamente nula. Se define el residuo f ′ (z) d f ′ (z) . El cociente = log f (z) (independiente de la logarı́tmico de f (z) en z0 como Res z=z0 f (z) f (z) dz rama del logaritmo) se denomina la derivada logarı́tmica de f (z). a) Si a es un cero de orden α de f (z) (α = 0, 1, 2, . . .), entonces f (z) = (z − a)α g(z) siendo g(z) analı́tica en z = z0 y g(z0 ) 6= 0. En este caso f ′ (z) α g ′ (z) = + f (z) (z − a) g(z) y por tanto Res z=a f ′ (z) = α. f (z) (12.91) (12.92) Es decir, el residuo logarı́tmico coincide con el orden del cero. b) Si b es un polo de orden β de f (z) (β = 0, 1, 2, . . .), entonces f (z) = analı́tica en z = z0 y g(z0 ) 6= 0. En este caso β g ′ (z) f ′ (z) =− + f (z) (z − b) g(z) 141 g(z) siendo g(z) (z − b)β (12.93) y por tanto Res z=b f ′ (z) = −β. f (z) (12.94) Es decir, el residuo logarı́tmico coincide con menos el orden del polo. Teorema. Sea C una curva cerrada, simple, suave a trozos y con orientación positiva. Sea f (z) analı́tica sobre C y en su interior, excepto en un número finito de polos, b1 , . . . , bn de órdenes β1 , . . . , βn (en el interior), con un número finito de ceros, a1 , . . . , am , de órdenes α1 , . . . , αm , también situados en el interior de C. Entonces, Z ′ m n X X 1 f (z) dz = αk − βk =: N − P. (12.95) 2πi C f (z) k=1 k=1 Demostración: f (z) es meromorfa, y por tanto también lo es su derivada logarı́tmica. La fórmula se deduce inmediatamente del teorema de los residuos ya que las únicas singularidades del integrando están en ak o bk . Teorema. (Principio de variación del argumento.) Sea N el número total de ceros y P el número total de polos (en cada caso contando cada uno con su multiplicidad) en la condiciones del teorema anterior: Z ′ Z 1 1 f (z) 1 dz = ∆C arg f (z). (12.96) d log f (z) = N −P = 2πi C f (z) 2πi C 2π Este resultado se conoce como el principio de variación del argumento. ∆C arg f (z) representa la variación de arg f (z) al recorrer C. Esta variación no depende de dónde se empiece a recorrer la curva cerrada ni de la rama que se elija para la función multivaluada arg w que se ha de elegir por continuidad a lo largo de la curva C.53 En la última igualdad se ha usado que log |f (z)| es univaluada y por tanto su variación al recorrer C se anula. Cuando C se recorre una vez en el plano z, w = f (z) recorre una curva cerrada Γ (no nece1 sariamente simple) en el plano w. ∆C arg f (z) no es más que el número de veces que Γ rodea 2π w = 0, es decir, el ı́ndice de Γ respecto de w = 0: N − P = n(Γ, 0). 53 (12.97) Obviamente si la función f (z) misma es multivaluada en el plano complejo, el principio se puede aplicar trabajando en su superficie de Riemann. En particular, C debe ser cerrada sobre su superficie de Riemann. 142 Ejemplo. Sea f (z) = z m , m ∈ Z y C la curva z(t) = Reit , 0 ≤ t ≤ 2π. En este caso Γ es la curva w = Rm eimt . Γ rodea w = 0 m veces: n(Γ, 0) = m. (Véase la fig. 45.) Por otro lado, 0 m>0 m m > 0 0 m=0 N = 0 m=0 P = (12.98) 0 m<0 −m m < 0 y en conjunto N − P = m. ♦ z w w m=1 m= 1 Figura 45: A la izquierda curva C en el plano Z. A la derecha curvas Γ en el plano w para m = ±1. 12.4. Teorema de Rouché Teorema. (Rouché.) Sean f (z) y g(z) analı́ticas sobre una curva C cerrada, simple, suave a trozos y también en su interior. Si |f (z)| > |g(z)| para z ∈ C, entonces f (z) y f (z) + g(z) tienen el mismo número de ceros en el interior de C. Demostración: |f (z)| > |g(z)| ≥ 0 sobre C garantiza que f (z) no se anula sobre C, y tampoco f (z) + g(z) se anula sobre C (por |f (z) + g(z)| ≥ |f (z)| − |g(z)| > 0.) Por otro lado, g(z) ∆C arg(f (z) + g(z)) = ∆C arg f (z) 1 + = f (z) g(z) = ∆C arg f (z) + ∆C arg 1 + . (12.99) f (z) Como |g(z)/f (z)| < 1 para z ∈ C, w = 1 + g(z)/f (z) recorre Γ que está contenida en el disco g(z) = 0. Esto implica |w − 1| < 1, por tanto Γ no encierra w = 0 y ∆C arg 1 + f (z) ∆C arg(f (z) + g(z)) = ∆C arg f (z). 143 (12.100) es decir, dado que no hay polos, por el principio de variación del argumento se deduce Nf +g,C = Nf,C . (12.101) El número de ceros de f + g en el interior de C es el mismo que el de f . ♦ Ejemplo. ¿Cuántos ceros tiene la función h(z) = z 8 − 4z 5 + z 2 − 1 en el disco |z| ≤ 1? Solución: Sea f (z) = −4z 5 , g(z) = z 8 + z 2 − 1. Se ve que |f (z)| > |g(z)| en |z| = 1, ya que |f (z)| = 4, |g(z)| = |z 8 + z 2 − 1| ≤ |z 8 | + |z 2 | + 1 = 3. El número de ceros de f (z) es 5 (un cero quı́ntuple), por tanto h(z) también tiene 5 ceros en |z| ≤ 1. Teorema. (Teorema fundamental del álgebra.) Todo polinomio de grado n ≥ 1 tiene exactamente n ceros (contando cada cero tantas veces como su multiplicidad). Demostración: Sea P (z) = a0 + · · · + an z n , n ≥ 1, an 6= 0. Aplicamos el teorema de Rouché con f (z) = an z n , g(z) = a0 + · · · + an−1 z n−1 . En la circunferencia |z| = R Pn−1 k g(z) a0 + · · · + an−1 z n−1 ≤ k=0 |ak |R −→ 0, = |z| = R (12.102) f (z) R→+∞ an z n |an |Rn por lo tanto |g(z)| < |f (z)| para |z| = R y R suficientemente grande. El número de ceros de P (z) = f (z) + g(z) será el mismo que el número de ceros de f (z) = an z n , a saber, n. Éstos son todos los ceros que hay ya que P (z) → ∞ cuando z → ∞ y no hay ceros en el infinito. ♦ El mismo teorema se puede probar usando el teorema de Liouville. 12.5. Prolongación analı́tica Recordemos que de acuerdo con el teorema de unicidad de funciones analı́ticas si f1 (z) y f2 (z) son analı́ticas en un dominio G, y coinciden en E ⊂ G tal que E tiene un punto de acumulación en G entonces coinciden en todo G. En particular, si coinciden en el entorno de un punto de G lo hacen en todo G. Ejemplo. ez es la única función analı́tica (en C) que coincide con ex definida en R. Ejemplo. La relación cos2 (z) + sen2 (z) = 1 en C se deduce por unicidad de la relación cos2 (x) + sen2 (x) = 1 en R. En efecto, si cos2 (z) + sen2 (z) vale 1 sobre el eje real, debe también ser 1 en C ya que cos2 (z) + sen2 (z) es entera y 1 es la única función entera que vale 1 sobre R. 144 (Análogamente, relaciones del tipo (ez )−1 = e−z , etc, se deducen de las correspondientes relaciones en R.) Definición. Sea f0 (z) analı́tica en un dominio G0 , y f (z) analı́tica en G tal que G0 ⊂ G y f0 (z) = f (z) en G0 , entonces f (z) es la extensión (o prolongación) analı́tica de la función f0 (z) a G. Por el teorema de unicidad esta extensión es única.54 También se puede hablar de extensión analı́tica desde un conjunto E con punto de acumulación aunque no sea un dominio. Por ejemplo, ez es la extensión analı́tica de la función ex definida en R. ∞ X 1 es la única prolongación analı́tica de la función f0 (z) = z n , definida 1−z n=0 en G0 = {|z| < 1} a G = C − {1}. Z +∞ e−zt dt. Esta integral converge en G0 = { Re z > 0}. En este caso Ejemplo. Sea f0 (z) = Ejemplo. f (z) = 0 1 1 f0 (z) = . La función f (z) = es su extensión analı́tica a G = C − {0}. z z Obsérvese que en la discusión anterior se sabe que f (z) es analı́tica en G ⊃ G0 . Otra cuestión es si dada f0 (z) analı́tica en G0 admite alguna extensión a algún dominio G mayor. Si por ejemplo f0 (z) = ∞ X n=0 an (z − z0 )n , G0 = {|z − z0 | < R0 }, (12.103) en algunos casos (es decir, dependiendo de los coeficientes an ) puede ocurrir que no haya extensión fuera de G0 . (Esto requiere que todos los puntos de la frontera sean singulares). En este caso |z − z0 | = R0 es la frontera natural de f0 (z). P n! Ejemplo. La función definida en |z| < 1 por f (z) = ∞ tiene |z| = 1 como frontera n=1 z natural. (Para un demostración véase el libro de Silverman.) En otros casos, desarrollando en torno a z1 ∈ G0 puede obtenerse una nueva serie f1 (z) en un disco G1 = {|z − z1 | < R1 } 6⊂ G0 . (Véase la fig. 46.) El radio de convergencia R1 llega hasta la singularidad más próxima. Se dice que (f0 (z), G0 ) y (f1 (z), G1 ) son extensión analı́tica directa uno de otro. En este caso se ha extendido f0 (z) definida sólo en G0 a una función analı́tica f (z) definida en un dominio mayor G = G0 ∪ G1 . Usando repetidamente este método, como en la fig. 54 Todas las funciones a que nos referimos son univaluadas. 145 zs G 1 z G 0 z 1 0 Figura 46: El desarrollo en z1 llega a puntos fuera de G0 . El punto zs es singular y determina la frontera de ambos dominios G0 y G1 . 31, página 99, puede llenarse el dominio de analiticidad de la función f (z) a base de discos. Los pares (fi (z), Gi (z)) se denominan elementos de la función analı́tica f (z).55 Si el dominio G explorado por la extensión analı́tica es simplemente conexo la función f (z) que se obtenga será univaluada, resultado conocido como principio de monodromı́a. Si el dominio es múltiplemente conexo, f (z) puede ser multivaluada. Es decir, al ir encadenando discos Gi y volver a alcanzar el punto z0 mediante otro elemento (fn (z), Gn ) puede ocurrir que fn (z0 ) 6= f0 (z0 ). En este caso la función f (z) es multivaluada y la extensión analı́tica construye automáticamente su superficie de Riemann. Ejemplo. f0 (z) = ∞ X (−1)n+1 (z − 1)n en G0 = {|z − 1| < 1}. Éste es un elemento de n f (z) = log z en la rama log 1 = 0. Supongamos que se extiende a base de discos centrados en puntos zk siguiendo la circunferencia |z| = 1 en sentido positivo. Cada disco tendrá z = 0 en su frontera y por tanto tendrá radio Rk = 1. Cuando la cadena de discos llegue otra vez a z = 1 se obtendrá log 1 = 2πi. n=1 La función extendida analı́ticamente hasta ocupar un dominio máximo (incluyendo quizá una superficie de Riemann no trivial) se denomina función analı́tica completa. 55 Puede adoptarse el punto de vista de que la función es construida por este método en regiones de C donde no estaba definida o bien que la función ya existı́a y está siendo descubierta. El teorema de unicidad favorece el segundo punto de vista. 146 12.5.1. Principio de reflexión de Schwarz Como se ha visto, no se sabe a priori dónde se podrá extender una función (f0 (z), G0 ) (ya que las singularidades aparecen al explorar nuevas zonas). El siguiente teorema garantiza la extensión en casos particulares. Teorema. (Principio de reflexión de Schwarz.) Sea f0 (z) analı́tica en un dominio G0 , tal que A = G0 ∩ R 6= ∅ y f0 (x) ∈ R para x ∈ A. Entonces admite extensión analı́tica a G = {z|z ó z ∗ ∈ G0 } = G0 ∪ G∗0 y tal que f (z ∗ ) = (f (z))∗ en G. Demostración: En G1 = G∗0 definimos f1 (z) = (f0 (z ∗ ))∗ . Esta función es analı́tica en G1 : ∗ f1 (z) − f1 (z0 ) (f0 (z ∗ ))∗ − (f0 (z0∗ )∗ ) f0 (z ∗ ) − f0 (z0∗ ) ∗ = = −→ (f0′ (z0∗ )) . (12.104) ∗ ∗ z→z z − z0 z − z0 z − z0 0 El lı́mite existe luego f1 (z) es analı́tica. Además f0 (z) real sobre el eje real implica que coincide con f1 (z) en A. Por tanto, son extensión analı́tica una de otra y f (z) definida como f0 (z) en G0 y como f1 (z) en G1 es analı́tica en G = G0 ∪G1 . Por construcción es inmediato que cumple f (z ∗ ) = (f (z))∗ en G. ♦ Ejemplo. f0 (z) = log z en G0 = {|z − 1| < 1} en la rama log 1 = 0 cumple log(z ∗ ) = (log z)∗ . 147 13. 13.1. Transformada de Laplace Transformada de Laplace Definición. La transformada de Laplace de f (t) se define Z +∞ e−st f (t) dt := L{f (t)}(s) F (s) = (13.1) 0 La variable s es compleja en general. A menudo se simplifica la notación a L{f (t)} (sin (s)) y se sobreentiende que es una función de s y no de t. Nota: La definición en (13.1) corresponde a la transformada de Laplace Z +∞ unilateral. También se define a veces la denominada transformada de Laplace bilateral, e−st f (t) dt. −∞ Se puede considerar f (t) definida sólo en t > 0, o bien en ] − ∞, ∞[ pero tal que f (t) = 0 para t < 0. En este último caso se dice que la función f (t) es causal. Definición. Sea σ ∈ R y f (t) definida en 0 ≤ t < +∞. Se dice que f (t) es de orden exponencial σ si |f (t)| < Keσt para algún K > 0 y ∀t ≥ A > 0 Es decir, f (t) = O(eσt ) si no crece más deprisa que eσt cuando t → +∞. Teorema. Sea f (t) continua56 en 0 ≤ t < +∞ y de orden eσt , entonces L{f (t)} converge para Re s > σ. Demostración: L{f (t)} = Z +∞ e 0 −st f (t) dt = Z A e 0 −st f (t) dt + Z +∞ e−st f (t) dt. La primera integral existe por f (t) continua. La segunda es impropia. Si Re s < σ Z +∞ Z +∞ K −st e− Re (s) t Keσt dt < |e f (t)| dt < < +∞ Re s − σ A A y la integral converge. ♦ 56 En realidad basta que sea localmente integrable, es decir integrable Riemann en todo intervalo cerrado. 148 (13.2) A (13.3) Ejemplo. Calcúlese la transformada de Laplace de f (t) = tn , n = 0, 1, . . .. R +∞ Solución: L{tn } = 0 e−st tn dt. Converge para Re s > 0. n=0 n>0 +∞ +∞ 1 1 = , e−st dt = − e−st s s 0 0 Z +∞ Z +∞ −st e n L{tn } = e−st tn dt = tn d( ) = L{tn−1 } . −s s 0 0 Z L{1} = (13.4) n! Por tanto, L{tn } = n+1 , n = 0, 1, 2, . . .. La función se puede extender analı́ticamente a C − {0}. s ♦ a para Re s > 0 y a ∈ R. En efecto, + a2 Z +∞ Z +∞ −(s−ia)t 1 1 1 e − e−(s+ia)t −st . dt = − e sen(at) dt = 2i 2i s − ia s + ia 0 0 Ejemplo. L{sen(at)} = s2 (13.5) De hecho basta | Im a| < Re s. El resultado se extiende a una función meromorfa. ♦ Algunas propiedades de la transformada de Laplace: a) F (s) es analı́tica en Re s > σ. b) F (+∞) = 0. En efecto, si la integral converge para algún s, f (t) debe ser de orden exponencial para algún σ y la integral debe tender a cero para s → +∞. c) (Teorema del valor inicial.) f (0) = lı́ms→+∞ (sF (s)). d) (Teorema del valor final.) Si F (s) es analı́tica en Re s > 0, f (+∞) = lı́ms→0 (sF (s)). 13.2. Reglas operativas n n X X a) Linealidad. L{ ai fi (t)} = ai L{fi (t)}. i=1 i=1 P Si fi (t) = O(e ), L{ ni=1 ai fi (t)} está definida en Re s > σ = máx(σ1 , . . . , σn ). σi t b) Traslación. L{eat f (t)} = F (s − a). Converge en Re s > σ − Re a. 149 c) Transformada de la derivada. L{f ′ (t)} = sF (s) − f (0). Z Z +∞ +∞ ′ −st ′ −st +s En efecto, L{f (t)} = e f (t) dt = e f (t) 0 0 sF (s). Iterando, L{f (n) n (t)} = s F (s) − n X +∞ 0 e−st f (t) dt = −f (0) + sn−k f (k−1) (0), n = 0, 1, 2, . . . k=1 d) Derivada de la transformada. F (n) (s) = (−1)n L{tn f (t)}. Z +∞ Z +∞ dn (n) −st En efecto, F (s) = n e f (t) dt = (−t)n e−st f (t) dt. ds 0 0 1 dn 1 n! Ejemplo. L{1} = implica L{tn } = (−1)n n = n+1 . s ds s s Rt 1 e) Transformada de la integral. L{ 0 f (τ ) dτ } = L{f (t)}. s Z t Z t Z t d f (τ ) dτ = L{f (t)}. f (τ ) dτ } + En efecto, s L{ f (τ ) dτ } = L{ dt 0 t=0 0 0 Z +∞ 1 f ) Integral de la transformada. L{ f (t)} = F (σ) dσ (suponiendo que la integral exista). t s 1 1 En efecto, Sea φ(s) = L{ f (t)}. Entonces, φ′ (s) = (−1) L{t f (t)} = −F (s), es decir, t t Z +∞ F (σ) dσ, pero φ(+∞) = 0. φ(s) = φ(+∞) + s Definición. La función escalón (o función paso o de Heaviside) se denota H(x) (o también Θ(x)) y se define como 1 si x > 0 y 0 si x < 0. Usando H(x) se puede escribir, por ejemplo, Z +∞ Z +∞ f (x) dx = H(x − a)f (x) dx, a Z b f (x) dx = a Z −∞ +∞ −∞ H(b − x)H(x − a)f (x) dx La función H(t − a) es discontinua en t = a con un salto de una unidad. 150 a ≤ b. (13.6) 13.3. Transformada inversa de Laplace Definición. Sea f (t) definida para t > 0. Se dice que f (t) es la transformada inversa de Laplace de F (s), por definición si L{f (t)} = F (s). Se denota f (t) = L−1 {F (s)}. La existencia de L−1 {F (s)} requiere F (+∞) = 0. Teorema. f (t) = L−1 {F (s)} es única, excepto donde sea discontinua. Definición. Usamos la notación f1 (x) “=” f2 (x) para indicar que en cualquier intervalo finito las dos funciones f1 (x) y f2 (x) difieren a lo sumo en un número finito de puntos. Con esta notación, se tiene que L{f1 (t)} = L{f2 (t)} sii f1 (t) “=” f2 (t) bajo condiciones muy generales sobre f1 (t) y f2 (t). (Obviamente si f1 (t) y f2 (t) son iguales salvo en puntos aislados la integral que define la transformada de Laplace no cambia. Por tanto L−1 {F (s)} no puede ser única si no se invoca continuidad.) Ejemplo. L−1 { 1s e−sa } = H(t − a) (a > 0) no está definida en t = a: cualquier definición de H(0) da la misma transformada de L{H(t − a)}. 13.4. Reglas operativas n n X X a) Linealidad. L { ai Fi (s)} = ai L−1 {Fi (s)}. −1 i=1 i=1 b) Traslación. L−1 {F (s − a)} = eat f (t). Y también L−1 {e−sa F (s)} = f (t − a)H(t − a) para a > 0. c) Transformada inversa de la derivada. L−1 {F (n) (s)} = (−t)n L−1 {F (s)}. d) Transformada inversa del producto. Sean f1 (t) y f2 (t) las transformadas inversas de F1 (t) y F2 (t), entonces L−1 {F1 (s)F2 (s)} = f1 (t) ∗ f2 (t). Aquı́ se ha usado el producto de convolución Z +∞ f1 (t) ∗ f2 (t) := f1 (x)f2 (t − x) dx. (13.7) −∞ En nuestro caso, dado que f1 (t) y f2 (t) son causales (es decir, idénticamente cero cuando 151 t < 0) f1 (t) ∗ f2 (t) := Demostración: t 0 (para L−1 {}). f1 (x)f2 (t − x) dx +∞ Z L{f1 (t) ∗ f2 (t)} = Z −st Z t dt e dx1 f1 (x1 )f2 (t − x1 ) 0 0 Z +∞ Z +∞ = dt dx1 H(x1 )H(t − x1 )e−st f1 (x1 )f2 (t − x1 ) −∞ −∞ Z +∞ Z +∞ dx1 dx2 H(x1 )H(x2 )e−s(x1 +x2 ) f1 (x1 )f2 (x2 ) = −∞ −∞ Z +∞ Z +∞ −sx1 dx2 e−sx2 f2 (x2 ) dx1 e f1 (x1 ) = 0 0 = F1 (s)F2 (s). Ejemplo. L−1 { (13.8) (13.9) 1 eat − ebt 1 } = eat ∗ ebt = . s−as−b a−b Ejemplo. Calcúlese L−1 { 1 }. − 1) s2 (s Solución: Basta descomponer la función en fracciones simples y usar L−1 { 1 1 } = tn eat n+1 (s − a) n! n = 0, 1, 2, . . . (13.10) (El mismo método se aplica al ejemplo anterior.) 1 1 1 1 = − 2− + − 1) s s s−1 s2 (s L−1 { 13.5. 1 } = −t − 1 + et − 1) s2 (s (t ≥ 0). ♦ (13.11) Fórmula de inversión de Bronwich Teorema. Sea F (z) analı́tica en Re z > σ y tal que F (z) → 0 cuando z → ∞ en Re z > σ, 152 y sea γ > σ, entonces 1 L {F (s)} = 2πi −1 Z γ+i∞ etz F (z) dz γ−i∞ t ≥ 0. (13.12) Si además F (z) sólo tiene singularidades aisladas en puntos zk de Re z ≤ σ, y lı́mz→∞ F (z) = 0, entonces X L−1 {F (s)} = Res (etz F (z)) t ≥ 0. (13.13) k z=zk Z γ+i∞ 1 etz F (z) dz, t ≥ 0. Calculemos su transformada de Demostración: Sea f (t) := 2πi γ−i∞ Laplace. Para Re s > σ elegimos σ < γ < Re s: Z +∞ Z γ+i∞ Z γ+i∞ 1 F (z) −ts 1 tz dt e L{f (t)} = e F (z) dz = dz 2πi γ−i∞ 2πi γ−i∞ s − z 0 Z F (z) 1 dz = F (s). (13.14) = 2πi C − s − z Aquı́ C − es la curva cerrada que recorre γ + it, (−R ≤ t ≤ +R) y luego vuelve al principio siguiendo un arco de circunferencia γR− en Re z ≥ γ, y se sobreentiende el lı́mite R → +∞ (véase la fig. 47(a)). El Lema 1 se aplica. Si sólo hay singularidades aisladas en puntos zk , a la izquierda de Re z = γ y F (z) → 0 cuando z → ∞, se puede completar el camino γ + it, (−R ≤ t ≤ +R) con el arco γR como antes pero en Re z ≤ γ (véase la fig. 47(b)). Para R → +∞ la integral no cambia por el Lema 3. El teorema de residuos da entonces X f (t) = Res (etz F (z)) t ≥ 0. ♦ (13.15) k z=zk 1 . Se puede elegir σ = máx( Re a, Re b) (u otro valor mayor). (s − a)(s − b) F (z) es meromorfa sin polos en Re z > σ y lı́mz→∞ F (z) = 0: Ejemplo. F (s) = L−1 {F (s)} = Res z=a eat − ebt etz etz + Res = z=b (z − a)(z − b) (z − a)(z − b) a−b Ejemplo. Por aplicación directa del teorema, L−1 { 153 (t ≥ 0). ♦ 1 } = −t − 1 + et − 1) s2 (s (13.16) (t ≥ 0). γ +iR γ+iR γ γ R R z2 z s 1 γ iR γ iR (a) (b) Figura 47: (a) Aplicación del teorema de residuos para demostrar (13.12). (b) Ídem para demostrar (13.13). Ejemplo. (Solución de una ecuación diferencial.) Sea N (t), t ≥ 0 tal que dN (t) = −λN (t), dt λ > 0. (13.17) (Describe, por ejemplo, la desintegración de partı́culas de una muestra radiactiva siendo λ la probabilidad de desintegración por unidad de tiempo.) Se puede resolver mediante transformada de Laplace: Sea Ñ (s) = L{N (t)}, entonces, aplicando transformada de Laplace a la ecuación se obtiene una ecuación algebraica equivalente: sÑ (s) − N (0) = −λÑ (s), N (0) Ñ (s) = . s+λ (13.18) Aplicando (13.10) para n = 0 y a = −λ, resulta N (t) = N (0)e−λt . ♦ 154 (13.19) 14. Series de Fourier Sea f (x) una función definida en el intervalo [c, c + 2L[. (En general f (x) puede ser compleja, de variable real.) Se trata de aproximar, o reproducir esta función mediante una serie de funciones trigonométricas. Sin pérdida de generalidad podemos cambiar f (x) por una función periódica fP (x) de periodo 2L de modo que coincida con f (x) en [c, c + 2L[, a base copiar f (x) en cada periodo. Hay una biyección natural entre funciones definidas en un intervalo finito dado y funciones periódicas en R: fP (x) = fP (x + 2L), x ∈ R, 14.1. fP (x) = f (x), x ∈ [c, c + 2L[. (14.1) Forma compleja de la serie de Fourier Sea S(x) definida por la serie ( forma compleja de la serie de Fourier) S(x) = +∞ X αn einπx/L , n=−∞ x∈R (14.2) para ciertos coeficientes αn y L > 0. Si la suma converge,57 la correspondiente función S(x) es periódica S(x) = S(x + 2L) (14.3) debido a la misma propiedad de las funciones básicas einπx/L . Por otro lado, dada la suma S(x) los coeficientes quedan unı́vocamente determinados mediante 1 αn = 2L Z c+2L e−inπx/L S(x) dx. (14.4) c (Obsérvese que, siendo S(x) y e−inπx/L periódicas, el resultado de la integral no depende de c.) Esto se deduce inmediatamente de las relaciones de ortogonalidad entre las funciones básicas Z c+2L 1 e−inπx/L eimπx/L dx = δnm , n, m ∈ Z. (14.5) 2L c 57 En este contexto el lı́mite se define de forma simétrica: 155 P+∞ n=−∞ := lı́mN →+∞ PN n=−N . Aquı́ el sı́mbolo δnm denota la delta de Kronecker 1 n=m δnm = . 0 n 6= m (14.6) Usando las relaciones de ortogonalidad también es inmediato verificar la identidad de Parseval: 1 2L Z c+2L 2 c |S(x)| dx = +∞ X n=−∞ |αn |2 . (14.7) Otra propiedad interesante es S(x) = (S(x))∗ (es decir, S(x) real) sii α−n = αn∗ . (14.8) Definición. Una función f (x) definida en [a, b] se dice que es continua a trozos si es continua excepto a lo sumo en un número finito de puntos a = x0 < x1 < · · · < xN = b para los que existen los lı́mites f (xn + 0+ ) y f (xn − 0+ ), y éstos son finitos.58 La propiedad más notable es que esencialmente cualquier función periódica se puede representar mediante una serie compleja de Fourier. Especı́ficamente, Teorema. Sea f (x) definida en [c, c + 2L[, continua a trozos y con derivada continua a trozos. Y sean Z c+2L 1 e−inπx/L f (x) dx, n ∈ Z. (14.9) αn = 2L c Entonces la suma de la serie compleja de Fourier, (14.2), satisface S(x) = 1 fP (x + 0+ ) + fP (x − 0+ ) , 2 (14.10) donde fP (x) es la función periódica asociada a f (x). 58 Esto quiere decir, que S(x) = f (x) en [c, c + 2L] excepto en los puntos de discontinuidad: f (x) si f (x) continua en x ∈]c, c + 2L[ 1 + + (f (x + 0 ) + f (x − 0 )) si f (x) discontinua en x ∈]c, c + 2L[ (14.11) S(x) = 1 2 + + (f (c + 0 ) + f (c + 2L − 0 )) si x = c ó x = c + 2L 2 Obviamente, en los bordes sólo se requiere existencia y finitud de f (a + 0+ ) y f (b − 0+ ) . 156 Demostración: (Cualitativa.) Sea Sn (x) la suma truncada, y x ∈]c, c + 2L[ n X Sn (x) = αk eikπx/L k=−n n X = e ikπx/L k=−n 1 2L = donde se ha usado n X k=−n wk = Z c+2L c 1 2L Z c+2L e−ikπy/L f (y) dy c sen(π(y − x)(n + 1/2)/L) f (y) dy, sen(π(y − x)/2L) (14.12) wn+1 − w−n wn+1/2 − w−n−1/2 = para w = eikπ(x−y)/L . w−1 w1/2 − w−1/2 Nos interesa el lı́mite n → +∞. Para aligerar la notación definimos ǫ= Ahora interesa el lı́mite ǫ → 0+ Sn (x) = Z L , π(n + 1/2) (c+2L−x)/ǫ dξ (c−x)/ǫ ξ= y−x . ǫ sen ξ πǫξ/2L f (x + ǫξ). πξ sen(πǫξ/2L) (14.13) (14.14) x = 1, resulta, en el lı́mite59 sen x Z 0 Z +∞ sen ξ sen ξ + dξ S(x) = dξ f (x − 0 ) + f (x + 0+ ) πξ πξ −∞ 0 1 + + f (x − 0 ) + f (x + 0 ) . (14.15) = 2 Z +∞ Z 0 sen ξ sen ξ dξ dξ = = 1/2. Por periodicidad x es en realidad un punto cualquiera de por πξ πξ 0 −∞ R. ♦ Usando ahora, x ∈]c, c + 2L[, y lı́m x→0 Con la notación “=” introducida anteriormente, el teorema implica f (x) “=” +∞ X αn einπx/L , n=−∞ 59 c ≤ x ≤ c + 2L. Este paso al lı́mite es formal. Para una demostración rigurosa véase, por ejemplo, el libro de Dettman. 157 (14.16) Obsérvese que la convergencia no puede ser absoluta y uniforme si f (x) es discontinua o f (c) 6= f (c + 2L) ya que entonces S(x) serı́a una función continua. 14.2. Forma trigonométrica de la serie de Fourier Sean an = a−n 1 = L bn = −b−n Z 1 = L c+2L cos(πnx/L) S(x) dx, c Z c+2L sen(πnx/L) S(x) dx. (14.17) c Entonces 1 αn = (an − ibn ). 2 O también, an = αn + α−n , bn = i(αn − α−n ). Y S(x) = (14.18) +∞ X 1 (an − ibn )(cos(πnx/L) + i sen(πnx/L)) 2 n=−∞ +∞ X 1 = a0 + (an cos(πnx/L) + bn sen(πnx/L)) 2 n=1 (14.19) (donde se han utilizado las propiedades de paridad de los coeficientes y de las funciones trigonométricas.) Ésta es la forma trigonométrica de la serie de Fourier. Una ventaja respecto de la forma compleja es que S(x) es real sii los an y bn son todos reales. Como se indica en (14.17) los coeficientes an y bn también pueden obtenerse directamente a partir de S(x) (sin pasar por la forma compleja). Esto se basa en las propiedades de ortogonalidad de las funciones trigonométricas básicas. En efecto, sean u y v funciones cualesquiera del conjunto de funciones √ (14.20) 1/ 2, cos(πnx/L) (n > 0), sen(πnx/L) (n > 0) ∋ u, v, entonces 1 L Z c+2L c 1 u=v u(x)v(x) dx = 0 u= 6 v 158 (14.21) La identidad de Parseval toma la forma Z +∞ X 1 1 c+2L 2 2 |S(x)| dx = |a0 | + (|an |2 + |bn |2 ). L c 2 n=1 14.3. (14.22) Series de Fourier seno y coseno Para simplificar, aquı́ tomaremos c = −L, es decir, f (x) está definida en ] − L, L[. En este caso se cumple que f (x) = f (−x) (f (x) es par) sii bn = 0, f (x) = −f (−x) (f (x) es impar) sii an = 0. (14.23) Veamos que f (x) en ]0, L[ se puede expresar usando sólo cosenos o sólo senos. Para ello, definimos la función f (x) 0<x<L fp (x) = (14.24) f (−x) −L < x < 0 Por construcción, fp (x) tiene las propiedades i) es par, y ii) coincide con f (x) en ]0, L[. Si desarrollamos fp (x) en ] −L, L[ se obtiene Z Z 1 L 2 L p p bn = 0, an = cos(πnx/L) f (x) dx = cos(πnx/L) f (x) dx. (14.25) L −L L 0 Se deduce entonces que f (x) “=” +∞ X cn cos(πnx/L), 0<x<L (14.26) n=0 con 1 c0 = L Z L f (x) dx, 0 2 cn = L Z L cos(πnx/L) f (x) dx (n > 0) . (14.27) 0 Ésta es la serie de Fourier coseno de f (x). Análogamente, podemos definir fi (x) = f (x) 0<x<L −f (−x) −L < x < 0 159 (14.28) Esta función es impar y coincide con f (x) en ]0, L[. Sus coeficientes de Fourier cumplen Z Z 2 L 1 L i i sen(πnx/L) f (x) dx = sen(πnx/L) f (x) dx. (14.29) an = 0, bn = L −L L 0 Se deduce entonces que f (x) “=” +∞ X dn sen(πnx/L), 0<x<L (14.30) n=1 con 2 dn = L Z L sen(πnx/L) f (x) dx (n > 0) . (14.31) 0 Ésta es la serie de Fourier seno de f (x). 2.0 1.5 1.0 0.5 -3 -2 1 -1 2 3 Figura 48: Serie de Fourier en (14.32), sumada hasta n = 8. Ejemplo. Sea f (x) = x + 1 en ] − 1, 1[. Entonces f (x) “=” f (x) “=” f (x) “=” +∞ 2 X (−1)n 1− sen(πnx), π n=1 n +∞ 3 4 X 1 − 2 cos (2n + 1)πx , 2 π n=0 (2n + 1)2 +∞ 2 X 1 − 2(−1)n sen(πnx), π n=1 n −1 < x < 1 , 0 < x < 1, (14.33) 0 < x < 1, (14.34) para las series de Fourier, de Fourier coseno y de Fourier seno, respectivamente. 160 (14.32) 2 1 -3 -2 1 -1 2 3 -1 -2 Figura 49: Serie de Fourier coseno en (14.33), sumada hasta n = 4. 2 1 -3 -2 1 -1 2 3 -1 -2 Figura 50: Serie de Fourier seno en (14.34), sumada hasta n = 16. 14.4. Complementos La demostración de (14.16) se puede hacer alternativamente usando la delta de Dirac. Partiendo de (14.12) y notando la propiedad sen(x/ǫ) −→ δ(x) (14.35) ǫ→0+ πx resulta Z c+2L π(y − x)/2L S(x) = δ(y − x) f (y) dy sen(π(y − x)/2L) c = f (x), (14.36) donde f (x) sea continua. 161 15. 15.1. Transformada de Fourier Transformada de Fourier Definición. Sea f (x) definida en R, y k real. La función Z +∞ e−ikx f (x) dx =: F{f (x)}(k) F (k) = (15.1) −∞ (si la integral converge) se denomina transformada de Fourier de f (x). 1 Nota: Esta definición no es universal. También se define a veces como, √ 2π o con e+ikx ó e−2πikx , etc. Z +∞ e−ikx f (x) dx, −∞ A menudo se escribe simplemente F{f (x)}. También se usa la notación f˜(k). Obviamente, |eikx | = 1 (k real) implica que una Rcondición suficiente para que F (k) exista es +∞ que f (x) sea absolutamente integrable, es decir, −∞ |f (x)| dx < +∞. La función f (x) puede ser real o compleja, F (k) resulta ser compleja en general. En principio k es real ( transformada de Fourier real). Cuando se consideran k complejos, se obtiene la transformada de Fourier compleja. Como se ve la transformada de Fourier compleja puede relacionarse con la de Laplace (especialmente la bilateral) o Laplace inversa mediante una rotación de π/2 en el plano complejo k. 15.2. Transformada inversa de Fourier Teorema. Si f (x) es continua a trozos y lo mismo su derivada, y f (x) es absolutamente integrable, Z +∞ dk f (x) “=” eikx F (k) =: F −1 {F (k)}(x) . (15.2) 2π −∞ En los puntos de discontinuidad F −1 {F (k)} proporciona la semisuma de lı́mites por la derecha y la izquierda. Demostración: (Cualitativa.) Este resultado se obtiene como lı́mite del correspondiente a series 162 de Fourier. Para f (x) definida en ] −L, L[, las relaciones (14.9) y (14.16) pueden reescribirse como Z L e−ikn x f (x) dx = 2Lαn , (15.3) −L f (x) “=” +∞ X ∆kn n=−∞ 2Lαn ikn x e , 2π (15.4) donde se ha definido π πn , ∆kn = kn+1 − kn = . (15.5) L L Si se toma ahora el lı́mite L → +∞, kn tiende a ser una variable continua k por ∆kn → 0+ . Entonces, en (15.3) Z +∞ Z L −ikn x e−ikx f (x) dx (15.6) e f (x) dx → kn = En (15.4), 15.3. −∞ −L y por tanto P+∞ n=−∞ ∆kn → R +∞ −∞ 2Lαn → F (k). (15.7) dk y finalmente +∞ X 2Lαn ikn x f (x) “=” e → ∆kn 2π n=−∞ Z +∞ dk −∞ F (k) ikx e . ♦ 2π (15.8) Propiedades de la transformada de Fourier Obsérvese que las operaciones F{} y F −1 {} son casi idénticas, a saber, F −1 {f (x)}(k) = 1 F{f (x)}(−k), 2π (15.9) y en consecuencia, las propiedades que siguen valen también para F −1 {} (salvo cambios triviales). n n X X a) Linealidad. F{ ai fi (x)} = ai F{fi (x)}. i=1 i=1 b) Paridad. F{f (−x)} = F (−k). Se deduce que si f (x) es par o impar, F (k) lo mismo. c) Conjugación. F{(f (x))∗ } = (F (−k))∗ .60 Por lo tanto si f (x) es real F (k)∗ = F (−k). Si además f (x) es par F (k) es real y par y si f (x) es impar, F (k) es imaginario puro e impar. 60 O más generalmente (F (−k ∗ ))∗ si k es complejo. 163 d) Traslación. F{eiax f (x)} = F (k − a), F{f (x − a)} = e−iak F (k). 1 e) Dilatación. F{f (ax)} = F (k/a), a > 0. a f ) Derivada. F{f ′ (x)} = ikF (k), F{xf (x)} = iF ′ (k). Demostración: Z +∞ +∞ Z +∞ ′ −ikx ′ −ikx e−ikx f (x) dx = ikF (k), e f (x) dx = e f (x) − −∞ −∞ −∞ Z +∞ Z +∞ d i e−ikx f (x) dx = iF ′ (k). e−ikx xf (x) dx = (15.10) dk −∞ −∞ (Suponemos f (±∞) = 0 para que la integral converja). g) Identidad de Parseval. Z +∞ 2 −∞ |f (x)| dx = Z +∞ −∞ |F (k)|2 dk . 2π (15.11) Esta identidad implica que f (x) es de cuadrado integrable sii F (k) lo es. (Sólo transformada de Fourier real.) Demostración: De hecho se cumple una relación más general: Z +∞ Z +∞ Z +∞ Z +∞ dk dk ∗ ikx ∗ F1 (k)F2 (k) = F1 (k) e f2 (x) dx = f1 (x)f2∗ (x) dx. (15.12) 2π −∞ −∞ 2π −∞ −∞ h) Convolución. F{f1 (x) ∗ f2 (x)} = F1 (k)F2 (k) 1 F{f1 (x)f2 (x)} = F1 (k) ∗ F2 (k). 2π Demostración: Z Z +∞ −ikx dx e −∞ Z +∞ −∞ dy f1 (y)f2 (x − y) = +∞ dx e −ikx f1 (x)f2 (x) = −∞ = = Z Z Z (15.13) +∞ dy f1 (y)e−iky F2 (k) = F1 (k)F2 (k). (15.14) −∞ +∞ dx e −∞ +∞ −∞ −ikx f1 (x) +∞ −∞ dq iqx e F2 (q) 2π dq F1 (k − q) F2 (q) 2π 1 F1 (k) ∗ F2 (k). 2π 164 Z (15.15) i) F (0) = R +∞ −∞ f (x) dx. j) F{ F{f (x)}} = 2πf (−x). k) Analiticidad. Si f (x) = O(e−a± x ) cuando x → ±∞, para a− < a+ , entonces F (k) es analı́tica en la banda a− < Im k < a+ del plano complejo k. Demostración: Para x → +∞, |e−ikx f (x)| = e Im k x |f (x)| < Ke Im k x e−a+ x y la integral convergerá absolutamente si ( Im k − a+ ) < 0. Análogamente convergerá en x → −∞ si ( Im k − a− ) > 0. l) Continuidad y convergencia. Como regla, si f (x) tiene “buen comportamiento” localmente (más regular), F (k) tiene “buen comportamiento” en k → ∞ (más convergente) y si f (x) se comporta bien en el infinito F (k) lo hace bien localmente. Especı́ficamente 1 ) cuando k → ∞. 1) Si f (x) tiene n derivadas continuas (n = 0, 1, 2, . . .), F (k) = O( kn+2 2) Si f (x) es a lo sumo discontinua con salto finito, F (k) = O( k1 ) cuando k → ∞. 3) Si f (x) tiene un polo de orden n (en R) F (k) = O(k n−1 ) cuando k → ∞. 61 4) Si f (x) es infinitamente diferenciable F (k) va cero más deprisa que cualquier potencia inversa de k. 5) Si f (x) es analı́tica en una banda de anchura σ > 0 en el plano complejo x que contenga R, F (k) = O(e−σ|k| ) cuando k → ∞. 15.4. Ejemplos Ejemplo. Sea f (x) = e−x 2 /2a2 , a > 0. Calculemos F (k). Z +∞ 2 2 −x2 /2a2 F (k) = F{e }= dx e−ikx e−x /2a . (15.16) −∞ Aquı́ se usa el método de completar cuadrados : 2 a2 k 2 x2 1 x ikx + 2 = + iak + . 2a 2 a 2 Z +∞ 2 −a2 k2 /2 dx e−(x/a+iak) /2 . F (k) = e −∞ 61 El mismo comportamiento se obtiene si la singularidad en f (x) es de tipo δ (n−1) (x). 165 (15.17) (15.18) Podemos ahora definir z = x/a + iak, dz = dx/a, Z +∞+iak 2 −a2 k2 /2 dz e−z /2 . F (k) = ae (15.19) −∞+iak La integral en z es a lo largo del camino R + iak. Se puede cambiar a una integral a lo largo de R 2 ya que e−z /2 tiende a cero cuando Re z → ±∞ y entre los dos caminos no hay puntos singulares: Z +∞ √ 2 2 2 −a2 k2 /2 (15.20) F (k) = ae dz e−z /2 = 2π a e−a k /2 . −∞ 2 2 Este ejemplo ilustra las propiedades citadas en . f (x) = e−x /2a es infinitamente diferenciable √ 2 2 y F (k) = 2π a e−a k /2 cae rápidamente a cero cuando k → ±∞. De hecho más deprisa que exponencialmente, ya que f (x) es entera en el plano complejo. Y al revés, f (x) cae muy deprisa en ±∞ por lo que F (k) es infinitamente diferenciable. También se ve que la anchura de f (x), ∆x ∼ a, es inversamente proporcional a la anchura de F (k), ∆k ∼ 1/a, lo cual está de acuerdo con la respuesta de F{} a dilataciones. Ejemplo. Sea f (x) = e−a|x| , a > 0. Z 0 Z +∞ Z +∞ −ikx −ax −ikx −a|x| dx e−ikx eax dx e e + dx e e = F (k) = −∞ 0 −∞ Z +∞ 1 2a 1 + = 2 . = dx (e−ikx e−ax + eikx e−ax ) = a + ik a − ik k + a2 0 (15.21) Obsérvese que F (k) es analı́tica en | Im k| < a, como consecuencia de la caı́da exponencial del f (x). Por otro lado f (x) es continua pero no su derivada (en x = 0) y por ese motivo la caı́da de F (k) cuando k → ±∞ es sólo O(1/k 2 ). También es interesante verificar la transformada inversa explı́citamente. Z +∞ 2a dk ikx 2a −1 F { 2 } = e (a > 0). 2 k +a k 2 + a2 −∞ 2π (15.22) Esta integral se puede hacer usando el teorema de residuos en el plano complejo k. Si x > 0 se aplica el lema de Jordan (Lema 3) cerrando el contorno por arriba sin que cambie el valor de la integral. El contorno encierra el polo en k = ia. En cambio si x < 0 se cierra por abajo y el contorno orientado negativamente encierra el polo en k = −ia: ) ( 2πi i(ia)x 2a −ax e = e , x > 0 2a 2π 2(ia) F −1 { 2 = e−a|x| . (15.23) } = i(−ia)x 2a ax − 2πi e = e , x < 0 k + a2 2π 2(−ia) 166 15.5. Transformada de Fourier multidimensional Si f (~x) está definida para ~x ∈ Rn , se define Z ~ ~k ∈ Rn , ~ dn x e−ik·~x f (~x), F{f (~x)}(k) := n R Z dn k i~k·~x ~ −1 ~ e F (k). F {F (k)}(~x) := n Rn (2π) 15.6. (15.24) (15.25) Función escalón Definición. Se puede completar la definición de prescripción H(0) = 1/2, 0 H(x) = 1/2 1 la función escalón en x = 0 mediante la x<0 x=0 x>0 (15.26) El convenio H(0) = 1/2 no es universal.62 Esta prescripción cumple H(x) + H(−x) = 1. 15.6.1. Regularizaciones de H(x) H(x) se puede obtener como el lı́mite puntual de funciones continuas: H(x) = lı́m+ Hǫ (x) , ǫ→0 Hǫ (x) := h(x/ǫ) (15.27) siendo h(x) cualquier función continua tal que h(+∞) = 1, h(−∞) = 0 y h(0) = 1/2. Por ejemplo, x 1 1 arctan + π ǫ 2 Z x/ǫ 1 1 1 x 1 −x2 e dx = + erf 2) Hǫ (x) = + √ 2 2 2 ǫ π 0 0 x < −ǫ 3) Hǫ (x) = 21 (1 + x/ǫ) |x| < ǫ 1 x>ǫ 1) Hǫ (x) = 62 Para todo x 6= 0 se cumple H(x) + H(−x) = 1 y (H(x))2 = H(x), sin embargo no hay ninguna elección de H(0) que haga que estas propiedades sean válidas también en x = 0. 167 Z 1/ǫ −iwx Z 1 1 1 1 1/ǫ sen(wx) e 4) Hǫ (x) = − P dw = + dw 2 2πi w 2 π 0 w −1/ǫ Z +∞ −iwx e dw 5) Hǫ (x) = −P −∞ w + iǫ 2πi Todas estas regularizaciones cumplen Hǫ (0) = 1/2. 15.6.2. Transformada de Laplace de la función de escalón Z +∞ 1 Z +∞ e−st dt = a<0 s −st 0 Z L{H(t − a)} = e H(t − a) dt = +∞ e−as 0 a>0 e−st dt = s a 1 e−as = H(−a) + H(a). s s 15.6.3. (15.28) Transformada de Fourier de la función de escalón Dado que H(x) no es absolutamente integrable usamos una regularización para calcular la transformada de Fourier Z +∞ −ǫ|x| e−ikx H(x)e−ǫ|x| dx F{H(x)} = lı́m+ F{H(x)e } = lı́m+ ǫ→0 ǫ→0 −∞ Z +∞ 1 = lı́m+ e−(ǫ+ik)x dx = lı́m+ ǫ→0 ǫ→0 ǫ + ik 0 −i =: . (15.29) k − i 0+ La transformada de Fourier de H(x) existe como distribución. La prescripción −i 0+ no tiene efecto si k 6= 0 pero hace falta para decir cómo tratar el polo en k = 0 en integrales. Por ejemplo, si se calcula la transformada inversa: Z +∞ dk ikx −i −i −1 } = lı́m+ e . (15.30) F { + ǫ→0 k − i0 k − iǫ −∞ 2π 168 Este cálculo se hace por residuos y es análogo al de F −1 { k22a } en la sección . +a2 F −1 −i } = { k − i 0+ −ǫx e , x>0 = H(x). lı́m 0, x < 0 ǫ→0+ (15.31) (H(0) = 1/2 se obtiene si se elige P para regular k → ±∞.) Nótese que se calcula la integral con ǫ finito y se toma el lı́mite al final, y no al revés. Si se hubiera tomado otra prescripción para el polo k = 0, por ejemplo valor principal de Cauchy, se hubiera obtenido función distinta: F −1 {P −i } := k lı́m+ F −1 {H(|k| − ǫ) ǫ→0 −i 1 x 1 }= = H(x) − . k 2 |x| 2 (15.32) Las distintas prescripciones para tratar el polo producen funciones que difieren por una constante aditiva. El polo en k = 0 en F{H(x)}(k) refleja que H(x) no tiende a cero en ±∞. (H(x) no es de cuadrado integrable y su transformada de Fourier tampoco.) La caı́da lenta cuando k → ±∞ se debe a la discontinuidad en H(x). 15.7. Función δ de Dirac Definición. La función δ (delta) de Dirac se define como la derivada de la función escalón δ(t) = o equivalentemente Z d H(t) , dt (15.33) t δ(τ ) dτ = H(t) . (15.34) −∞ De acuerdo con esta definición δ(t) = 0 si t 6= 0 mientras que δ(t) = +∞ si t = 0. En realidad δ(t) no es propiamente una función sino unaZdistribución o función generalizada. Esto quiere decir que sólo tiene sentido en expresiones del tipo f (t)δ(t−a) dt donde f (t) es una función suficientemente regular. 15.7.1. Propiedad básica de δ(t) Como distribución δ(t), se define por su propiedad básica: 169 Teorema. Para cualquier función f (t) continua en t = t0 Z +∞ f (t) δ(t − t0 ) dt = f (t0 ). (15.35) −∞ Demostración: Z +∞ Z +∞ Z +∞ d d f (t) H(t − t0 ) dt = − f (t) dt = f (t0 ). f (t) δ(t − t0 ) dt = − dt0 −∞ dt0 t0 −∞ La propiedad básica también puede expresarse Z b f (t0 ) t0 ∈]a, b[ f (t) δ(t − t0 ) dt = 0 t0 ∈ 6 ]a, b[ a para a < b. (15.36) (15.37) En efecto, obviamente (15.37) implica (15.35), y también al revés: si a < b, Z b Z +∞ f (t) δ(t − t0 ) dt = H(b − t)H(t − a) f (t) δ(t − t0 ) dt = H(b − t0 )H(t0 − a) f (t0 ) (15.38) a −∞ que vale f (t0 ) si a < t0 < b y 0 si t0 < a ó b < t0 . ♦ R Nota: Obsérvese que ninguna función ordinaria D(x) puede cumplir f (x)D(x)dx = f (0) para toda función continua f (x), ya que f (x) podrı́a tomar valores arbitrarios en x 6= 0 sin cambiar la R integral y eso requerirı́a D(x) = 0 ∀x 6= 0. Cualquiera que fuera el valor de D(0) saldrı́a f (x)D(x)dx = 0 siempre. Más generalmente, si f (t) es continua a trozos y habiendo elegido H(0) = 1/2, Z +∞ 1 f (t) δ(t − t0 ) dt = (f (t0 + 0+ ) + f (t0 − 0+ )), 2 −∞ (15.39) que coincide con (15.35) si f (t) es continua en t = t0 . De nuevo, esta prescripción no es universal y no forma parte de la definición de δ(t). 15.7.2. Otras propiedades de δ(t) Algunas propiedades de la δ de Dirac: a) δ(−x) = δ(x). Se deduce derivando H(x) + H(−x) = 1. 1 b) δ(ax) = δ(x) para a > 0. Se deduce derivando H(ax) = H(x). a 170 15.7.3. Regularizaciones de δ(t) Definición. Una familia de funciones δǫ (t) es una regularización de la delta de Dirac si para cualquier f (t) continua en [a, b], Z b δǫ (t − t0 )f (t) dt = f (t0 ), a < t0 < b. (15.40) lı́m+ ǫ→0 a Si Hǫ (t) −→+ H(t) entonces δǫ (t) = ǫ→0 d Hǫ (t) es una regularización de δ(t), es decir, dt δǫ (t) −→+ δ(t). ǫ→0 (15.41) Usando las regularizaciones de H(t) anteriores se obtiene: 1) δǫ (t) = ǫ 1 , π t 2 + ǫ2 1 2 2) δǫ (t) = √ e−(t/ǫ) , ǫ π 3) δǫ (t) = 1 H(ǫ − |t|), 2ǫ sen(t/ǫ) . πt Z +∞ w dw 5) δǫ (t) = P e−iwt 2π −∞ w + iǫ 4) δǫ (t) = Todas estas regularizaciones δǫ (t) cumplen (15.39) al tomar el lı́mite. (De hecho, todas son funciones pares de t excepto la (5).) Nota: A menudo se ve en libros de texto la afirmación de que una regularización de la del 0 t 6= 0 ta es aceptable sii cumple las dos propiedades siguientes: (1) δǫ (t) −→+ y (2) +∞ t = 0 ǫ→0 Z +∞ δǫ (t) dt = 1. −∞ En realidad estas condiciones no son necesarias ni suficientes. 171 t<ǫ 0 sen(t/ǫ) Ejemplo. Tanto δǫ (t) = 1/ǫ ǫ ≤ t ≤ 2ǫ, como δǫ (t) = son regularizaciones πt 0 t > 2ǫ válidas y no cumplen (1). Obviamente (2) tampoco es necesaria (no hace falta que la integral valga 1 antes de tomar el lı́mite ǫ → 0+ ). R +∞ Las propiedades más relajadas (1′ ) lı́mǫ→0+ δǫ (t) = 0 si t 6= 0 y (2′ ) lı́mǫ→0+ −∞ δǫ (t) dt = 1, tampoco son suficientes. Ejemplo. Por ejemplo, ǫ 1 ǫ ǫ 1 2t d 0 t 6= 0 = − −→+ dǫ (t) := 1 + 2 2 2 2 2 2 2 +∞ t = 0 dt πt +ǫ πt +ǫ π (t + ǫ ) ǫ→0 (15.42) y también Z +∞ f (t)dǫ (t) dt = −∞ Z +∞ −∞ (f (t) − f ′ (t)) ǫ 1 dt −→ f (0) − f ′ (0), π t2 + ǫ2 ǫ→0+ (15.43) que vale 1 si f (t) = 1, y por tanto dǫ (t) está normalizada a uno. Sin embargo, dǫ (t) no tiende a δ(t) (ya que entonces darı́a f (0) en (15.43)) sino a δ(t) + δ ′ (t). ♦ Un método práctico de construir una regularización de la delta (aunque no la más general) es partir de una función D(t) tal que Z +∞ D(t) dt = 1 (15.44) −∞ Entonces 1 δǫ (t) := D(t/ǫ), ǫ (15.45) proporciona una regularización válida.63 En efecto, para a > 0 y f (t) continua en [−a, a], Z 63 a δǫ (t) f (t) dt = −a Z a/ǫ −a/ǫ D(t) f (ǫt) dt −→+ f (0) ǫ→0 Z +∞ D(t) dt = f (0). (15.46) −∞ En realidad, dada δǫ (t) basta que exista D(t) normalizada a 1 tal que lı́mǫ→0+ (ǫδǫ (ǫt) − D(t))/ǫ → 0. 172 15.7.4. Transformada de Laplace de δ(t) L{δ(t − a)} = 15.7.5. R +∞ 0 e−st δ(t − a) dt = H(a)e−as . Transformada de Fourier de δ(t) F{δ(x)} = Z +∞ e−ikx δ(x) dx = 1. (15.47) −∞ Esto permite la definición alternativa de la delta de Dirac como o explı́citamente: R +∞ −∞ F −1 {1} = δ(x), eikx dk 2π = δ(x) que proporciona la importante identidad Z +∞ eikx dk = 2πδ(x). (15.48) (15.49) −∞ Propiedades relacionadas: F{eiax } = 2πδ(x − a), F{cos(ax)} = π(δ(x − a) + δ(x + a)), F{sen(ax)} = −iπ(δ(x − a) − δ(x + a)). 15.8. Complementos 15.8.1. Transformada inversa de Fourier La demostración de (15.2) es sencilla usando la representación Z +∞ dw e−itw = δ(t) 2π −∞ de la delta de Dirac. En efecto, Z +∞ Z +∞ Z Z +∞ dk ikx +∞ −ikt dk ikx e F (k) = e δ(t − x)f (t) dt = f (x). e f (t) dt = −∞ 2π −∞ −∞ −∞ 2π 173 (15.50) (15.51) (15.52) 15.8.2. Identidad de Weierstrass 1 1 = P ∓ iπδ(x). + x ± i0 x (15.53) En efecto: La primera identidad es la conjugada de la segunda y ésta equivale a F −1 { 1 1 } = F −1 {P } + iπ F −1 {δ(k)}. + k − i0 k (15.54) Esta identidad se sigue de (15.31), (15.32): F −1 { k−i1 0+ } = iH(x) y F −1 {P k1 } = i(H(x) − 21 ), junto con F −1 {2πδ(k)} = 1. Nótese que esta fórmula es compatible con el Lema 4 de integración. Por ejemplo, si f (x) es analı́tica en R y se quiere calcular Z a f (x) dx, a>0 (15.55) P −a x se puede rodear el polo por arriba con una semicircunferencia γǫ− centrada en cero y luego sustraer esta contribución: Z −ǫ Z a Z Z a Z f (x) f (x) f (x) P + dx = lı́m+ dx + lı́m+ dx. (15.56) + ǫ→0 ǫ→0 x x −a x ǫ γǫ− −a γǫ En el lı́mite ǫ → 0+ , la primera integral se puede cambiar por una integral a lo largo del eje real moviendo el polo hacia abajo y la segunda se puede hacer con el Lema 4: Z a Z a f (x) f (x) P dx = lı́m+ dx + iπf (0) (15.57) ǫ→0 −a x −a x + iǫ es decir, P 1 1 = + iπδ(x). x x + i0+ 174 (15.58) 16. Bibliografı́a - T.M. Apostol, Análisis matemático, Ed. Reverté. - J.W. Dettman, Applied complex variables, McMillan Company (1984). - J. Peñarrocha et al., Variable complexa, Universitat de València (2006). - R.A. Silverman, Complex analysis with applications, Dover Publications Inc. (1984). - M.R. Spiegel, Variable compleja (serie Schaum), McGraw-Hill (1991). - M.R. Spiegel, Transformadas de Fourier (serie Schaum), McGraw-Hill (1991). - M.R. Spiegel, Transformadas de Laplace (serie Schaum), McGraw-Hill (1991). - A.D. Wunsch. Variable compleja con aplicaciones, Addison-Wesley Iberoamericana (1997). 175 Integrales y series A. Tablas proporcionadas por J. Nieves. R∞ R∞ 2 π 1: 0 (x2dxx = 16a (a > 0) 2: −∞ 3, +a2 )3 R∞ R ∞ dx 2π √ 4: −∞ 3: 0 1+x 3 = 3 3 R ∞ dx R∞ π √ 5: 0 1+x 6: −∞ 4 = 2 2 7: 9: R∞ dxx6 −∞ (x4 +a4 )2 R∞ 0 sen2 xdx x2 R∞ = = √ 3 2π , 8a π 2 = x sen xdx 1+x4 = π2 e R∞ sen(πx)dx x(1−x2 ) =π 19: R∞ x sen xdx (a2 +x2 )2 21: R∞ cos xdx (1+x2 )3 13: 15: 17: 23: 25: 27: 29: 0 R∞ 0 0 Rπ 0 3π 8 0 = = R∞ 12: −1 √ 2 sen √12 14: 16: sen2n xdx = π (2n−1)!! (2n)!! 0 8: 10: sen3 xdx x3 11: (a > 0) πe−a , 4a (a > 0) 7π 16e dx a+b cos x+c sen x R 2π dθecos θ sen(nθ − sen θ) = 0 26: xdx 1+x5 28: 0 R∞ 0 R∞ = 2π sig(a) √ a2 −b2 −c2 2 2 (a > b + c2 ) x2 dx −∞ 1+x6 = = π 5 sen π 3 2π 5 x2 −x+2 dx x4 +10x2 +9 = dx (x2 +a2 )(x2 +b2 )2 sen xdx x R∞ =π = = πe−m (m+1) , 4 = R∞ cos xdx x2 +a2 πe−a , 2a R 2π dx a+b sen x 0 R∞ = sen xdx −∞ (x2 +1)(x+2) 0 π(a+2b) , 2ab3 (a+b)2 (a, b > 0), a 6= b π 2 dx cos(mx) (x2 +1)2 0 5π 12 = (m > 0) (a > 0) = π5 (cos 2 − 1/e) 2π 1 (a2 −b2 ) 2 , (a > 0, a2 > b2 ) 1 = −πi, γ : |z − 2| = 4 dzz cos z−1 h −a i R∞ e cos xdx π e−b , (a, b > 0), 20: 0 (x2 +a = − 2 )(x2 +b2 ) 2(b2 −a2 ) a b (a 6= b) √ R ∞ cos axdx 3 √π sen π + a e−a 2 , (a > 0) 22: 0 1+x 2 +x4 = 6 2 3 R 2π 24: 0 (a+bdx = 22πa2 3 , (a > b > 0) cos x)2 18: R 2π 0 0 dx 1+x2 R γ (a −b ) 2 30: R 2π 0 R∞ 0 dθecos θ cos(nθ − sen θ) = x sen axdx x2 +m2 R∞ −∞ 176 2π , n! (n = 0, 1, 2, . . .) = sig(a) π2 e−|a|m , (a, m ∈ R) 0, |p| > 1 sen t ipt π, |p| < 1 , p ∈ R e dt = t π , |p| = 1 2 R∞ p cos x2 dx = 0 sen x2 dx = 21 π2 √ R∞ 2 Ayuda: 0 dre−r = 2π R∞ mxdx = mπ π −mπ 33: −∞ cos ex +e−x e 2 +e 2 R ∞ √x 35: 0 1−x2 dx = − π2 √ R∞ 3π 2 1 dx = 37: 0 √x(1+x 2 )2 8 √ h √ i Rb (x−a)(b−x) a+b ab = π − 39: a dx x 2 31 R∞ 32 0 34: 36: 38: 40: 43: 45: 47: 49: 51: 53: R∞ 0 R∞ 0 log x dx x2 +a2 π 2|a| = log x (x3 +1)(x−1) √ log x 2 2 dx x(1+x ) Ra q 0 R5 1 dx 3 x(x−1) x 0 x2 +a2 R∞ 0 R∞ 1: 3: 5: 7: 9: 0 = (−1)n n=1 (4n2 −1)2 P∞ 1 n=0 (2n+1)2 11: 1 n=1 n4 Pn=∞ + 4) 46: = 48: 1 4 = π 2 cos π2 4 π 8 (a > 0) −1 + log2 |a| R∞ 0 R∞ 0 R1 e dx 1+e x = √ x dx (1+x)2 xp−1 dx 1−x π 8 = = π 2 cos(πa) sen2 (πa) − 1 2 π2 8 1 n=−∞ n4 +n2 +1 √ √π tanh( π 3 ) 2 3 π , tan πp (0 < p < 1) π dx = R∞ log x dx 1+x4 = − 8π√2 log2 x dx 1+x4 = √ 3π 3 2 64 log2 x dx 1+x2 = π3 8 i 50: 52: 0 R∞ 0 R∞ 0 R1 cos π8 1 24 sen(pλ) π sen(πp) sen λ = 2 1 1 0 1 (1+x)[x2 (1−x)] 3 Ra q x2 0 x2 +a2 R∞ 0 4: 6: 177 1 = 2 4 πa cos 5π + 8 = R∞ π , 2 cos(aπ/2) −iωt −∞ dω eω+iǫ |a| < 1 1, t > 0 1/2, t = 0 , t ∈ R = 0, t < 0 1 n=−∞ n2 +a2 = πa cotanh(πa) (−)n n=2 n2 −1 1 4 P∞ = P∞ (−)n−1 n sen(nθ) n2 +α2 P∞ 1 n=1 4n2 −1 n=1 P∞ n=1 πa 2 (a > 0) cosh(ax) dx cosh(x) −1 2πi 3 π4 √ 3 dx = a−x dx x P∞ 10: = = (0 < a < 1) π 2 x−p dx 1+2x cos λ+x2 0 8: π4 90 = R∞ 2: = π , sen(πa) 1 0 (1+x2 )[x(1−x)] 12 54: lı́mǫ→0+ π2 6 (−)n n=−∞ (n+a)2 P∞ 44: π4 15 P∞ P∞ 19π 2 108 √ − π162 (3π h π 2|a| = 3 1 n=1 n2 42: = log 56 dx exx−1 = P∞ = a−x dx x log2 x dx x2 +a2 log |a| dx = R∞ ax −∞ (|p| < 1, |λ| < π, p, λ ∈ R) (0 < a < b) 41: R∞ (−1)n n4 = = 1 2 −7π 4 720 = π sinh(αθ) , 2 sinh(απ) (|θ| < π) B. Transformada de Laplace (http://www.engineering.com/Library/ArticlesPage/ tabid/85/articleType/ArticleView/articleId/129/Laplace-Transforms.aspx ) 178 C. Ejercicios 1. Calcúlense las siguientes expresiones: (3 + 4i)(2 + i) √ 3 + 4i , 2 − i, , 1−i (1 + 2i)(3 − 4i) 1 − iz z+i (z 6= −i). 2. Demuéstrense las siguientes propiedades a) |z1 z2∗ + z1∗ z2 | ≤ 2|z1 z2 |, b) La ecuación de la recta que pasa por z1 y z2 (z1 6= z2 ) es Im z − z1 = 0. z2 − z1 √ √ √ 3. Calcúlese el argumento principal de ( 3 + i)/(− 2 + i 2). 4. Sea Arg z el argumento de z tomado en [0, 2π[ y Argα z el argumento tomado en [α, α + 2π[. Pruébese que Argα z = α + Arg (e−iα z). 5. Demuéstrese la propiedad Im (z1 z2 · · · zn ) = Pn k=1 z1 ∗ · · · zk−1 Im z k zk+1 · · · zn∗ . √ 6. Calcúlese (−2 − i2 3)1/3 expresando el resultado en coordenadas polares. 7. Obténgase tan(3θ) en función de tan θ aplicando el teorema de Moivre. 8. Sean wk , k = 0, 1, . . . , n − 1, las n raı́ces n-ésimas distintas del número complejo z. Pruébese n−1 X que wk = 0 , para n = 2, 3, 4, . . . k=0 9. Hállense los puntos lı́mite de las siguientes sucesiones: a) zn = 1 + (−1)n n , n+1 n , n+1 n c) zn = e((iπ/n) ) . b) zn = 1 + in 179 10. Encuéntrense los puntos de acumulación (o puntos lı́mite) de los siguientes conjuntos de puntos: i 1 + , (m, n = ±1, ±2, ...) m n p q b) z = + i , (m, n, p, q = ±1, ±2, ...) m n c) |z| < 1 a) z = 11. a) Demuéstrese que una sucesión compleja zn = xn + iyn converge al lı́mite α = a + ib si y sólo si lı́mn→∞ xn = a, lı́mn→∞ yn = b. b) Pruébese que si zn → α para n → ∞, entonces |zn | → |α| para n → ∞. Demuéstrese que el recı́proco no es cierto. z∗ . z→0 z 12. Muéstrese que no existe el lı́mite lı́m 13. Sea P (z) un polinomio con coeficientes reales, P (z) = n X k=0 ck z k , ck ∈ R . Demuéstrese que la soluciones en C de P (z) = 0, o son reales o aparecen en pares complejos conjugados. 14. Exprésese la función f (z) = 2x + y + i(x2 + y 2 ) como un polinomio en z y z ∗ . 15. Demuéstrese que z 2 es uniformemente continua en {z |z| < 1} pero no en C. 16. Sea f (z) = 1/z 2 . Esta función no es invertible si se define sobre C − {0}. Encuéntrese algún dominio de definición E ⊂ C − {0}, tal que (a) E sea un dominio (región abierta) y (b) la función inversa sea univaluada (o equivalentemente, f restringida a E sea inyectiva). Obténgase el recorrido correspondiente, E ′ = f (E). 17. Hállese la imagen de la banda 1 ≤ x ≤ 2 en el plano z bajo la transformación ω = z 2 . αt + β , −∞ ≤ t ≤ +∞, es una circunferencia (quizá degeγt + δ nerada, supónganse valores genéricos para los coefcientes α, β, γ, δ). Determı́nese la posición de su centro y su radio. 18. Demuéstrese que la curva z(t) = 180 iz 2 + 3 . z→∞ z 2 − iz 19. Aplı́quese la regla de l’Hôpital para calcular lı́m h i h i (x + y)2 . Demuéstrese que lı́m lı́m f (z) = lı́m lı́m f (z) y sin embargo no 20. Sea f (z) = 2 x→0 y→0 y→0 x→0 x + y2 existe el lı́mite lı́m f (z). z→0 21. Demuéstrese que la función u = diferenciable en ese punto. p |xy| tiene derivadas parciales en x = y = 0 pero no es 1 en forma binómica u(x, y) + iv(x, y) y verifı́quese que se satisfacen las z ecuaciones de Cauchy-Riemann, excepto para z = 0. Calcúlese f ′ (z) usando la forma binómica 1 y verifı́quese que coincide con − 2 . z 22. Exprésese f (z) = 23. La exponencial compleja se define como ez := ex (cos y + i sen y). Verifı́quese que se satisfacen la ecuaciones de Cauchy-Riemann en todo C (y por tanto ez es una función analı́tica en C, ya que u y v son diferenciables). Calcúlese su derivada. 24. Obténganse las √ ecuaciones de Cauchy-Riemann en función de las variables polares r y θ. Verifı́quese que z es derivable, excepto en r = 0. 25. (a) Verifı́quese que las condiciones de Cauchy-Riemann pueden expresarse como (∂x +i∂y )f (z) = 0. (b) Sea F (z1 , z2 ) analı́tica como función de las dos variables complejas z1 y z2 . Demuéstrese que f (z) := F (z, z ∗ ) satisface las ecuaciones de Cauchy Riemann sii F (z1 , z2 ) no depende de z2 . 26. Sean f1 (z) = u1 + iv1 y f2 (z) = u2 + iv2 dos funciones analı́ticas. Verifı́quese en forma explı́cita que f3 (z) = f1 (z)f2 (z) también satisface las ecuaciones de Cauchy-Riemann. Lo mismo para f4 (z) = f1′ (z). y es armónica excepto en el origen. Encuéntrese + y2 una función armónica conjugada, u, y la correspondiente función analı́tica f (z) = u + iv. I 28. Hállese el valor de la integral (z 2 − z ∗ ) dz, siendo C la circunferencia |z| = 2 (orientada 27. Verifı́quese que la función v(x, y) = y − positivamente). x2 C (Sol. − 8πi.) 181 29. Calcúlese la integral Z (2,8) (1,2) a) la parábola y = 2x2 . x2 − iy 2 dz a lo largo de b) la lı́nea recta que une los dos puntos. (Sol. (Sol. 511 3 511 3 − 49 i.) 5 − 14i.) Demuéstrese que la parte real de la integral no depende del camino. 30. Calcúlese el valor de la integral I |z|2 dz alrededor del cuadrado con vértices en los puntos (Sol. −1 + i.) 0, 1, 1 + i, i y orientación positiva. 31. Sea C la curvaZ y = x3 − 3x2 + 4x − 1 que une los puntos 1 + i y 2 + 3i. Calcúlese el valor 12z 2 − 4iz dz . (Sol. −156 + 38i.) de la integral C 1 dz, n = 1, 2, . . ., siendo C una curva simple n C (z − a) cerrada suave a trozos y orientada positivamente, y z = a un punto de su interior. (Sol. I = 2πi si n = 1, I = 0 si n ≥ 2.) 32. Obténgase el valor de la integral 33. Calcúlese el valor de la integral trozos que no pasen por z = 0. 34. Obténgase el valor de la integral |z − 1| = 1. I Z zb za I 1 dz, siendo za = −i y zb = i, sobre curvas suaves a z (Sol. i(π + 2πk), k entero.) (z ∗ )2 dz alrededor de las circunferencias (a) |z| = 1 y (b) (Sol. (a) 0, (b) 4πi.) 1 dz donde C es el cuadrado con vértices en los puntos + 2z + 2 C 0, −2, −2 − 2i y −2i y orientación positiva. (Sugerencia: descompóngase el integrando en fracciones simples.) (Sol. − π.) 35. Calcúlese la integral Z z2 36. Obténgase el ı́ndice de la curvas (a) {z(t) = cos(t) eit , 0 ≤ t ≤ 2π} y (b) {z(t) = cos(t) + i sen(2t), 0 ≤ t ≤ 2π}, respecto de un punto arbitrario del plano complejo que no sea de la curva. 182 37. Encuéntrese el dominio de convergencia de las series (a) ∞ X z 2k+1 , k=0 (b) ∞ X zk √ , k! k=0 (c) ∞ X k=1 zk . k(k + 1) (Sol. (a) |z| < 1, (b) |z| < ∞, (c) |z| < 1.) 38. Hállense todas las soluciones de las ecuaciones (a) exp z = i , (b) cos z = 2 , (c) log z = i . 39. Derı́vense las ecuaciones de Cauchy-Riemann en coordenadas polares usando que log(z) es una función analı́tica. 40. Se usa la notación f (0+ ) (donde f (z) es una función cualquiera) con el significado f (0+ ) := lı́m f (ǫ) . Calcúlese (a) Log (R ± i0+ ), (b) [(R ± i0+ )i ]p (donde [z w ]p denota la deterǫ→0 ǫ>0 minación principal de z w , z, w ∈ C). En ambos casos R > 0. 41. Calcúlese z i , iz , z z , ii y en particular sus correspondientes determinaciones principales. 42. Encuéntrese la expresión de tan−1 z en función del logaritmo. 43. Determı́nense las superficies de Riemann de las funciones (a) f (z) = log((z − a)(z − b)), (b) f (z) = log((z − a)/(z − b)), donde a, b ∈ C, a 6= b. Buscar los puntos de ramificación, elegir cortes de rama, etc. 44. Encuéntrese el desarrollo en serie de Taylor de −1 a) (1 + z 2 ) , alrededor de z = 0. −1 b) z , alrededor de z = 1 (Sol. (Sol. P∞ P∞ n=0 (−1) n n=0 (−1) n 2n z .) (z − 1)n .) 45. Sea α un número complejo arbitrario. Desarróllese en serie de Taylor la función (1 + z)α alrededor de z = 0, para la rama en la que la función toma el valor ei2παk en z = 0. α(α−1)···(α−n+1) n α(α−1) 2 i2παk z + · · · , |z| < 1 + αz + 2 z + · · · + (Sol. f (z) = e n! 1 si α no es natural, si lo es, f (z) es entera.) 46. Consideremos la rama de log w que toma el valor 0 cuando w = 1. (Por ejemplo, tomando arg w ∈] − π, π[.) 183 a) Desarróllese log(1 + z) en serie de Taylor alrededor de z = 0 y determı́nese el radio de ∞ X zn convergencia. (Sol. (−1)n−1 , R = 1.) n n=1 1+z b) Hágase lo mismo para la función f (z) = log . 1−z ∞ X z 2n+1 (Sol. 2 , R = 1.) 2n + 1 n=0 47. Hállese el desarrollo en serie de Taylor de sech z = 1/ cosh z en torno a z = 0 hasta orden z 4 inclusive, y determı́nese el radio de convergencia de la serie. 48. Sea f (z) analı́tica en 1 ≤ |z| ≤ 2 y tal que |f (z)| < 3 sobre |z| = 1 y |f (z)| < 12 sobre |z| = 2. Demuéstrese que |f (z)| < 3|z|2 en 1 ≤ |z| ≤ 2. 49. Sea f (z) una función entera y no constante. Pruébese que M (r) = máx{|f (z)|, |z| = r} es una función estrictamente creciente, esto es, si r1 < r2 entonces M (r1 ) < M (r2 ). 50. Hállense los valores máximo y mı́nimo del módulo de la función f (z) = eiz cuando z está en la región cerrada y acotada cuya frontera es la curva 9x2 + y 2 = 9. 51. Estúdiense las singularidades de la función (z 2 − 1) (z − 2)3 . f (z) = sen3 (πz) (Sol. Polos triples en z ∈ Z excepto z = 2 que es evitable y z = ±1 que son polos dobles.) 52. Obténganse los desarrollos en serie de Laurent de las funciones siguientes alrededor de los puntos indicados: P∞ exp(2z) 2n+3 n 2 , z = 1. (Sol. e n=−3 (n+3)! (z − 1) , 0 < |z − 1| < ∞.) 3 (z − 1) P∞ (−1)n 2n z − sen z , z = 0. (Sol. b) n=0 (2n+3)! z , |z| < ∞.) z3 1 , z = −2. c) (z − 3) sen z+2 i P∞ (−1)n h 1 5 − , 0 < |z + 2| < ∞.) (Sol. n=0 (2n+1)! (z+2)2n (z+2)2n+1 a) 184 d) 1 1 cosh , z = 0. z z 53. Desarróllese la función f (z) = a) |z| < 1 b) 1 < |z| < 3 c) 3 < |z| d) 0 < |z + 1| < 2 (Sol. P∞ 1 1 n=0 (2n)! z 2n+1 , 0 < |z| < ∞.) 1 en serie de Laurent para (z + 1)(z + 3) P n −n−1 n (Sol. 12 ∞ )z .) n=0 (−1) (1 − 3 P P∞ (−1)n n n −n ].) (Sol. − 12 [ ∞ n=0 3n+1 z + n=1 (−1) z P ∞ (Sol. 21 n=2 (−1)n (3n−1 − 1)z −n .) P 1 n n (Sol. − 14 ∞ n=0 (− 2 ) (z + 1) .) 54. Obténgase la parte principal del desarrollo de Laurent de decir, para el desarrollo válido en 0 < |z − 2πi| < R). 1 alrededor de z = 2πi (es − 1)2 ez − 1 . z 3 (z − 1)2 55. Obténgase el residuo en z = 0 de f (z) = 56. Demuéstrese que cosh(z+z −1 ) = b0 + (ez P∞ n=1 bn (z n +z −n ) siendo bn = 1 2π R 2π 0 cos(nθ) cosh(2 cos θ) dθ. 57. Calcúlense las integrales 4, 25, 26, 16, 3, 15, 11, 46, 39, 52 y 40, indicadas en el apéndice . 58. Calcúlense las series indicadas en el apéndice . 59. Calcúlense las siguientes integrales usando métodos de variable compleja: Z 2π 2π 2n 2n cos θ dθ. (Sol. 2n .) a) n 2 0 Z 2π 2π 2n 2n sen θ dθ. (Sol. 2n b) .) n 2 0 Z 2π 1 √ 1 2 .) dθ, a, b reales, |b| < |a|. (Sol. 2π c) a 1−(b/a) a + b sen θ 0 Z 2π 1 2πa d) dθ, 0 < b < a. (Sol. (a2 −b 2 )3/2 .) 2 (a + b cos θ) 0 185 60. Evalúense las integrales Z +∞ 1 a) dx. 1 + x4 0 Z ∞ 1 b) dx. 2 2 −∞ (x + 4x + 5) Z +∞ 1 c) dx. 4 x + x2 + 1 0 Z +∞ 1 dx, d) (x2 + a2 )(x2 + b2 ) 0 (Sol. π √ .) 2 2 (Sol. π2 .) (Sol. a, b > 0. (Sol. 61. Encuéntrese el valor de las integrales siguientes Z +∞ x sen(bx) a) dx, a, b > 0. x 2 + a2 −∞ Z +∞ sen x dx. b) x 0 Z +∞ sen2 x c) dx. 2 2 2 −∞ x (π − x ) π √ .) 2 3 π .) 2ab(a+b) (Sol. πe−ab .) (Sol. π/2.) (Sol. 1/π.) 62. Calcúlense las integrales (con valor principal de Cauchy en su caso) I 1 exp(zt) a) dz, siendo C el cuadrado con vértices en ±1 ± i. (Sol. 1 − cos(t)/2.) 2πi C z (z 2 + 1) Z a+i∞ 1 exp(zt) −t √ dz, a > −1, t > 0. (Sol. √e πt .) b) 2πi a−i∞ z+1 Z ∞ exp(ax) π 1 .) c) dx, 0 < a < b. (Sol. ) b sen( πa −∞ 1 + exp(bx) b 63. Evalúense las integrales siguientes Z +∞ −a x a) dx, |a| < 1. 1 + x2 0 Z +∞ x−a b) dx, |a| < 1, |α| < π. x2 + 2x cos α + 1 0 Z +∞ log x dx. c) 1 + x2 0 186 (Sol. (Sol. π 1 .) 2 cos( π2 a) π sen αa .) sen α sen πa (Sol. 0.) d) Z ∞ 0 e) log2 x dx. 1 + x2 Z +∞ Z +∞ 0 f) 0 g) Z h) Z +∞ 0 b a i) Z b a j) Z 1 0 k) Z 0 1 (Sol. π 3 /8.) log x dx, (x − a)2 + b2 0 < b < |a| reales. (Sol. 1 [π 2b − arctan ab ] log(a2 + b2 ), con 0 < arctan ab < π.) cosh ax dx, cosh x −1 < a < 1. xα log x dx, x 2 + a2 a > 0, −1 < α < 1. ((x − a)(b − x))−1/2 dx, ((x − a)(b − x))1/2 dx, r 1 x 1 dx, 1 + x 1 + λx 1 − x r 1 x dx. 1+x 1−x (Sol. (Sol. π/2 .) cos(πa/2) πaα−1 π π tan α].) π [log a + 2 cos 2 α 2 2 a < b. (Sol. π.) (Sol. (b − a)2 π/8.) a < b. λ > 0. (Sol. 64. Sea la función compleja de variable compleja: f (z) = z2 + π2 . senh z π λ−1 √1 2 − q 1 1+λ (Sol. π 1 − √1 2 .) .) a) Decir qué singularidades tiene y de qué tipo son. b) Hállese el desarrollo de Laurent en un entorno reducido de z = 0 hasta orden z 4 inclusive. ¿Cuál es el dominio de convergencia de dicho desarrollo? I c) Calcúlese el valor principal de la integral f (z) dz donde C es la curva cerrada orientada C en dirección positiva formada por la semicircunferencia C1 y el tramo de recta C2 . C1 está centrada en iπ y va del punto 0 al punto 2πi por el semiplano derecho. C2 es el segmento recto que une 2πi con 0. (Sol.: (a) Singularidades evitables: ±iπ, polos simples: iπk con k = 0, ±2, ±3, . . . . 2 2 (b) π 2 z1 + (1 − π3! )z + 3!1 ( 7π − 1)z 3 + O(z 5 ) con 0 < |z| < 2π. (c) −iπ 3 .) 60 √ R +∞ 2 65. Sabiendo que 0 e−x dx = 2π encuéntrese el valor de las integrales R +∞ cos x R +∞ sen x pπ pπ √ dx, √ dx. , b) .) a) 0 b) (Sol. a) 2 2 0 x x 187 +∞ +∞ X X 1 1 . (Sugerencia calcúlese primero .) 66. Calcúlese la suma 2 2 2 n n + a n=−∞ n=1 I 1 zP ′ (z) dz 67. Demuéstrese que si P (z) es un polinomio no idénticamente nulo, entonces 2πi C P (z) es la suma de las raı́ces de P (z) con su multiplicidad, siendo C una circunferencia muy grande orientada positivamente. 68. Usando el principio del argumento, determı́nese el número de raı́ces de z 4 + z 3 + 4z 2 + 2z + 3 en cada uno de los cuatro cuadrantes. (Sol. 0, 2, 2, 0.) 69. Aplı́quese el teorema de Rouché para determinar el número de soluciones que tienen las ecuaciones siguientes en los dominios especificados: a) z 8 − 4z 5 + z 2 − 1 = 0 en |z| < 1. (Sol. 5.) b) z 4 − 5z + 1 = 0 en 1 < |z| < 2. (Sol. 3.) c) z 2 − cos z = 0 en |z| < 2. (Sol. 2.) d) f (z) = z en |z| < 1, si f (z) analı́tica y |f (z)| < 1 en |z| ≤ 1. z n e) e = 3z en |z| < 1. 70. (Sol. 1.) (Sol. n.) R∞ a) Demuéstrese que f1 (z) = 0 (1 + t)e−zt dt converge únicamente si Re z > 0. Hállese la función que prolonga analı́ticamente f1 (z) al resto del plano complejo. P∞ n P∞ z+i n 1 b) Sea f2 (z) = 1+i y f (z) = 3 n=0 z (estando cada función definida en su n=0 1+i dominio de convergencia). Pruébese que una función es prolongación analı́tica directa de la otra. 71. Usando el principio de reflexión de Schwarz: a) Sea f1 (z) analı́tica en Re (z) ≥ 0 e imaginaria pura sobre el eje real. Si f1 (1 + i) = 15 − 4i, determı́nese el valor de su extensión analı́tica en z = 1 − i. b) Demostrar que f2 (z ∗ ) = (f2 (−z))∗ siendo f2 (z) definida y analı́tica en un dominio G simétrico respecto el eje imaginario (y con intersección no vacı́a con el eje imaginario) y f2 (z) toma valores reales sobre el eje imaginario. 72. Usando las propiedades generales de la transformada de Laplace, encuéntrense las transformadas de las siguientes funciones: (Sol. n!/(z − a)n+1 .) a) Θ(t)tn eat , n = 1, 2, 3, . . . (Sol. z/(z 2 − ω 2 ).) b) Θ(t) cosh(ωt). (Sol. eab e−az (z − b)−1 [(z − b)−1 + a].) c) tΘ(t − a)ebt , a > 0 . 188 d) Rt 0 (Sol. z/[(z + 1)(z 2 + ω 2 )].) e−τ cos(ω(t − τ )) dτ . 73. Resuélvase la siguiente ecuación integro-diferencial: Z t dy + y(τ )dτ = e−t , t ≥ 0, dt 0 y(0+ ) = a. 1 (Sol. y(t) = [(1 + 2a) cos t + sen t − et ].) 2 74. Resuélvase la ecuación diferencial y ′′ + 3y ′ + 2y = e−t , t > 0, con las condiciones y(0+ ) = a, y ′ (0+ ) = b, usando transformada de Laplace. (Sol. yp = −e−t + te−t + e−2t , yc = (b + 2a)e−t − (a + b)e−2t , y = yp + yc .) 75. Resuélvase el sistema de ecuaciones diferenciales: x′ + y ′ − x + y = e−t , x′ − y ′ + x + y = e−2t , para t > 0 con las condiciones x(0+ ) = a, y(0+ ) = b. (Sol. x = 35 + a cos t + 3 3 3 −2t y = a + 5 sin t + b − 10 cos t + 10 e .) 3 10 − b sin t − 21 e−t − 1 −2t e , 10 76. Hállese la transformada de Fourier real de f (t) = e−at Θ(t), donde Θ(t) es la función escalón 1 .) y a > 0. Compruébese la transformación inversa directamente por integración. (Sol. a + ix 77. Hállese la transformada de Fourier compleja de Θ(t) cos(ωt). Demuéstrese que la transformación es analı́tica para Im (z) < 0. Inviértase la transformación mediante una integral de iz contorno. (Sol. 2 .) ω − z2 78. Demuéstrese que la transformada de Fourier compleja de e−t 2 /2 es e−z 2 /2 . 79. Obténgase la transformada de Fourier de Θ(x) y sign(x) y verifı́quense las transformadas inversas. 80. Hállense las siguientes transformadas complejas: F{Θ(t) cosh(ωt)}, F{Θ(t) senh(ωt)}. iz ω (Sol. − 2 , − 2 .) 2 z +ω z + ω2 81. Hállense las siguientes transformadas complejas: F{Θ(t)t cosh(ωt)}, F{Θ(t)t senh(ωt)}. 2ωzi ω2 − z2 , 2 .) (Sol. 2 2 2 (z + ω ) (z + ω 2 )2 189 82. Encuéntrese una solución de dy d2 y + 3 + 2y = e−|t| usando la transformada de Fourier. dt2 dt et 2 1 (Sol. y(t ≤ 0) = , y(t > 0) = e−2t − e−t + te−t .) 6 3 2 190
© Copyright 2026