1. No category

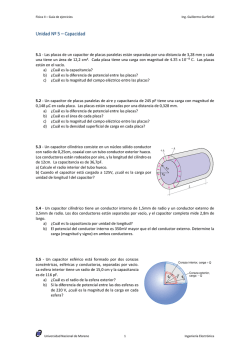
Física III
Trabajo Práctico 6
14/5/2015
Experiencias en clases teóricas
En esta sección Ud. encontrará algunos cuestionarios y guías sobre temas y demostraciones experimentales realizadas en las
clases en el anfiteatro. El objetivo de esta parte es que Ud. preste mucha atención a las experiencias desarrolladas y que a partir
de sus observaciones y de una investigación adicional con bibliografía adecuada, o con la realización de sus propios
experimentos Ud. complemente y reafirme sus conocimientos de los temas desarrollados.
Importante: Los temas desarrollados en las experiencias serán evaluados en los parciales y en los exámenes finales.
Capacitores
Para realizar la siguiente experiencia se necesita, una fuente de tensión de 12 volt DC, una fuente de tensión 220 volt DC, un
Capacimetro Digital, Placas de cobre con pertinaz de distinta dimensiones, cables de conexión, capacitores de distintos tipos,
Prolongador.En esta unidad trataremos de ver como es el comportamiento de la capacidad:
1ro.- respecto al cambio en sus dimensiones.
2do.- usando como separador un dieléctrico.
3ro.- influencia de d con la tensión
a) ¿Qué consideraciones tiene que tener en cuenta cuando se compra un capacitor?
b) Tiene alguna influencia el tipo de material conductor utilizado en la fabricación de capacitores. ¿Por qué
c) Si tenemos un capacitor de 22 uf el cual se carga con una tensión de 20Volt si queremos aumentar la carga 10 veces ¿Cómo
lo haría?
d) En un capacitor de un determinada dimensiones y 25 volt de trabajo, que es lo que estamos variando al ponerle un dieléctrico
entre sus caras.e) Si se tiene dos capacitores de 1 uF/25 DC y se los conecta en serie o en paralelo. ¿Qué parámetro estamos variando en cada
caso y cual seria su valor?
Problemas
P1- Una esfera metálica de radio a=1cm tiene depositada y distribuida en forma uniforme en su superficie una carga eléctrica
Q=1 C.
(a) Calcule el potencial eléctrico de la esfera.
(b) Defina y determine la capacidad eléctrica o capacitancia de esta configuración. Haga un análisis detallado de las unidades en que
se mide la capacitancia. Defina la unidad Faradio y las unidades: miliFaradio (mF), microfaradio (μF), nanoFaradio (nF) y
picoFaradio (pF).
(c) Calcule la energía potencial eléctrica de la configuración.
P2- Sobre dos discos metálicos iguales de radio a = 1cm, aislados, se depositan cargas eléctricas +Q y
–Q de modo que sus densidades superficiales de carga son σ+ =10-6C/m2 y σ-= -10-6C/m2
respectivamente. Se disponen paralelamente separados una distancia d=0,5mm entre ellos. En la figura
1 se indica el esquema eléctrico del sistema.
(a) Calcule el campo eléctrico y dibuje las líneas de campo eléctrico de esta configuración de
conductores. Explique si realizó simplificaciones para hacer sus cálculos.
(b) Calcule la diferencia de potencial eléctrica entre las dos placas.
(c) Defina y calcule la capacitancia entre las placas.
(d) ¿Cuánto vale la energía almacenada en el sistema? ¿En qué lugar físico del espacio está
almacenada esta energía?
(e) Indique cómo cambian los resultados anteriores si: (i) la carga depositada inicialmente se duplica,
(ii) la distancia entre las placas aumenta al doble, (iii) la superficie de las placas aumenta al cuádruple.
Figura 2
Figura 1
P3- Calcule la capacitancia de un capacitor de placas metálicas esféricas y
concéntricas de radios ra=1cm y rb=2cm (Figura 2).
(a) Si la diferencia de potencial entre ambas placas es de 10 V ¿Cuál es el valor de la
carga eléctrica depositada en las placas?
(b) ¿Cuánto vale la energía eléctrica contenida entre las placas? ¿Hay energía
eléctrica correspondiente a este sistema adentro de la esfera de radio ra? ¿Hay
energía eléctrica correspondiente a este sistema afuera de la esfera de radio r1b?
Demuestre y explique detalladamente sus respuestas.
(c) Si se duplica el valor de carga calculado en el punto anterior calcule y explique
cómo se modifican: i) la diferencia de potencial entre las placas, ii) la capacitancia,
iii) la energía contenida entre las placas.
(d) ¿Cuál es la máxima carga que puede soportar el capacitor? Explique.
P4- Calcule y grafique el campo y el potencial en todo el espacio para un coaxil formado
por un conductor central cilíndrico de radio a=1mm, cargado con 1=0,1 C/m y un
conductor externo, concéntrico de radio interior b=4mm, espesor d=0,1mm y cargada con
2 = -0,1 C/m (Figura 3). Calcule la capacitancia por unidad de longitud de este sistema.
P5- En la figura 4 se muestra una batería alimentando dos
capacitores conectados en serie.
(a) Dibuje el circuito eléctrico equivalente de esta
conexión.
Figura 3
(b) Determine cuál será la capacitancia equivalente
conectada a la batería.
(c) Determine la diferencia de potencial en cada capacitor.
(d) Generalice sus respuestas para el caso de tener más de dos
capacitores en serie.
(e) ¿Para qué se usan en la práctica este tipo de conexiones? Explique.
Figura 4
P6- En la figura 5 se muestra una batería alimentando dos capacitores conectados en paralelo.
(a) Dibuje el circuito eléctrico equivalente de esta conexión.
(b) Determine cuál será la capacitancia equivalente conectada a la batería.
(c) Determine la carga acumulada en cada capacitor.
(d) Generalice sus respuestas para el caso de tener más de dos capacitores en paralelo.
(e) ¿Para qué se usan en la práctica este tipo de conexiones? Explique.
C
C
1
2
C
3
P7- (a) Encuentre las expresiones de la capacitancia equivalente en el
circuito de la figura 6. Datos: C1= C3= 2 F, C2= 1 F, C4= 10 F.
(b) ¿Cómo conectaría varios condensadores de 1 y 2 F para obtener una
capacidad equivalente de 4,5 F?
Figura 5
C
P8- Un condensador de placas
paralelas (vacío entre las
placas) se conecta a una batería V0, como se indica en la
secuencia (1) de la figura 7. Si después de un tiempo prolongado
se desconecta la batería:
(a) ¿Qué diferencia de potencial entre las placas mide el
voltímetro dibujado en la secuencia (2)? ¿Qué cantidad de carga
se acumuló en las placas?
(b) Si se introduce entre placas un material aislante de constante
dieléctrica k (secuencia (3)) ¿Cuál es la lectura del voltímetro y
la cantidad de carga acumulada en las placas en este caso?
Describa lo que ocurre en el dieléctrico. ¿Cómo calcularía la
Figura 7
densidad de carga inducida en el dieléctrico?
Si ahora, a partir de la secuencia (4) se introduce el mismo material aislante entre
placas pero sin desconectar la batería (secuencia (5)). ¿Cuál es la lectura del
voltímetro, y la cantidad de carga acumulada en este caso?
Figura 6
4
P9- Un capacitor tiene placas paralelas (dimensiones 2cmx3cm) separadas por una
lámina de papel de 1mm de espesor. Utilice los datos provistos por la tabla 1.
(a) Calcule la capacitancia del dispositivo.
(b) ¿Cuál es la máxima diferencia de potencial que se puede aplicar entre placas?
¿Por qué existe esta limitación? Explique detalladamente.
(c) ¿Cuál es la máxima energía que puede ser almacenada en este capacitor?
(d) Calcule la densidad superficial de carga inducida en el material dieléctrico.
(e) Encuentre las expresiones de los vectores campo eléctrico, polarización
eléctrica y desplazamiento. Defina la susceptibilidad eléctrica ¿Cómo queda
expresada la Ley de Gauss en este caso?
P10- Considere que en el capacitor del punto anterior las placas están separadas
por aire. Realice los mismos cálculos solicitados en el problema anterior. Compare
y discuta los resultados y saque conclusiones.
Tabla 1- (Fuente: Halliday-Resnick-Krane)
P11- Observe nuevamente la tabla 1 ¿Porqué la rigidez dieléctrica del vacío figura con
valor infinito? Investigue y responda.
P12- En un capacitor de placas paralelas de área A se introduce una lámina de cobre tal
como se indica en la figura 8 y se aplica una diferencia de potencial V entre las placas
originales.
(a) Indique la distribución de cargas en la lámina de cobre.
(b) Encuentre la capacitancia del dispositivo antes y después de introducir la lámina.
Figura 8
P13- Si en el espacio entre placas del condensador plano se colocan dos placas de un material
dieléctrico, según las configuraciones indicadas en la figura 9, encuentre las expresiones de la
capacitancia equivalente en cada caso.
Sección adicional
Hay antecedentes que indican que el
capacitor eléctrico fue inventado por un
científico alemán llamado Ewald Georg
von Kleist en noviembre de 1745.
Algunos meses más tarde, Pieter van
Musschenbroek, un profesor holandés de
Figura 9
la Universidad de Leyden, desarrolló un
dispositivo muy similar, conocido como
la “jarra de Leyden”, al que por lo general se la considera el primer capacitor. Mucho ha servido este aparato en los inicios de la
investigación de los fenómenos eléctricos y de sus aplicaciones técnicas.
Actualmente sus aplicaciones tecnológicas son innumerables. Realice una investigación usando bibliografía e internet y escriba
un breve informe describiendo el principio físico de funcionamiento y los materiales empleados para fabricar las originales jarras
de Leyden. Agregue a su informe una descripción del principio de funcionamiento de una aplicación moderna de los capacitores
tal como su empleo en el touchpad de las notebooks o la touchscreen de notebooks, smartphones, tablets, smart tvs.
Busque también en internet el tema de los llamados “supercondensadores” y explique para qué sirven, de qué están compuestos,
cómo almacenan energía.
Problema de parcial
En la figura se presenta un capacitor de placas paralelas (A=115cm2, d=1,24cm) al cual se le aplicó una diferencia de potencial
con una batería V0=85,5 V. Se retira la batería y se inserta una lámina dieléctrica (K=2,61) de espesor b=0,78cm.
(a) Calcule la capacitancia antes de introducir la lámina dieléctrica y el valor de las cargas libres en las placas.
(b) Aplicando la ley de Gauss calcule el campo eléctrico dentro de la lámina dieléctrica. Calcule la energía eléctrica contenida en
la lámina dieléctrica.
(c) Si la máxima tensión que puede soportar el capacitor (entre placas) es de 100 voltios DC en vacío ¿Cambiará el valor de esta
tensión cuando se coloca un dieléctrico en el capacitor? ¿Por qué?
Figura 2