1. No category

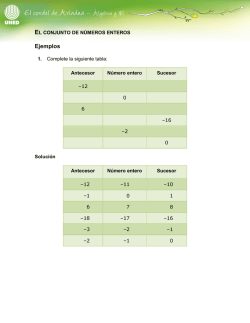
Seminario de Solución de Problemas de Métodos Matemáticos I
Actividad 2
Seminario de Solución de Problemas de
Métodos Matemáticos I
Conceptos Preliminares de Álgebra Lineal y
Teoría de Números
Actividad 2: Congruencias módulo 𝑚
"Las matemáticas poseen no sólo la verdad, sino cierta belleza suprema. Una belleza fría y
austera, como la de una escultura”
--Bertran Russell.
Definición: Sea 𝑚 ∈ ℕ, 𝑚 ≠ 0. Dos números enteros 𝑎, 𝑏 ∈ ℤ son congruentes
modulo 𝑚 si 𝑚|(𝑎 − 𝑏). En tal caso, se escribe 𝑎 = 𝑏𝑚𝑜𝑑 𝑚 .
Teorema: Sea 𝑚 ∈ ℕ, 𝑚 ≠ 0. Para cualquier 𝑎 ∈ ℤ Existe 𝑟 ∈ ℕ 𝑡𝑎𝑙 𝑞𝑢𝑒 0 ≤ 𝑟 < 𝑚
y 𝑎 = 𝑟𝑚𝑜𝑑 𝑚
Reportes entregables:
Nota: La entrega será en archivo pdf (Portable Document Format) de
acuerdo con las instrucciones de su Asesor.
1. Encontrar 2 enteros positivos y 2 negativos equivalentes a 38 (𝑚𝑜𝑑 3).
2. Encuentra el residuo módulo 5 de:
a) 374 + 49(801) + 120
b) 1622 + 22(846) +
c) 5684 − (224)13 − 16
d) 654 − 12(530) + 29
3. Encontrar el dígito de las unidades de 2(325) + 3(87 ) + 5104 + 1235 , en
modulo 10.
4. Se tienen 2003 tarjetas numeradas, se remueven de 3 consecutivas
en 3 consecutivas hasta quedar 2. Juan dice que quedó la tarjeta 1002.
¿Miente o dice la verdad?
5. Escribir las tablas de suma y producto para ℤ2 , ℤ3 , ℤ4 , ℤ5 , ℤ6 ,
ℤ9 , ℤ11 . Escribir los inversos aditivos y multiplicativos.
6. Un vendedor de naranjas quiere saber cuántas naranjas tenía ayer.
Sólo recuerda que eran más de 100 pero menos de 150 y que cuando
hacía montones de 2, 3, 4, 5, y 6 naranjas siempre sobraba 1.
Mat. Laura Cortés