1. No category

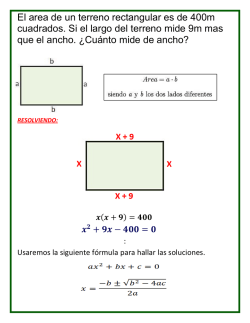
1
Aplicaciones de las derivadas
Resuelve cada uno de los siguientes problemas.
Ejercicios
1) Encuentra dos números cuya suma sea 30 y cuyo producto sea máximo
2) ¿Qué número excede a su cubo en la mayor cantidad?
3) Encuentra dos números positivos cuyo producto sea 20 y la suma de sus cuadrados sea mínima.
4) Sea x un número positivo. Demuestra que x + 1/x nunca será menor a 2.
5) Un granjero dispone de 1 200 metros de cerca para limitar un terreno rectangular contiguo a un
río de curso rectilíneo. No se requiere cercar en la orilla del río. ¿Cuáles son las dimensiones
del terreno con área máxima?
6) Un pedazo de estambre de 50 centímetros de largo se corta en dos partes; una parte se dobla
para formar un cuadrado, y la otra para formar una circunferencia. ¿A qué distancia de una
de las orillas se debe hacer el corte para que la suma de las áreas del cuadrado y de la circunferencia sea el máximo?
7) ¿Cuáles son las dimensiones de un campo rectangular de área A = 2 400 m2 que requiere la
menor cantidad de cercado?
8) Demuestra que de todos los rectángulos con un área fija A, el de menor perímetro es el
cuadrado.
9) Una página impresa debe contener 432 cm2 de material impreso. Debe tener margenes de 3
cm a los lados y de 2 cm arriba y abajo. ¿Cuáles han de ser las dimensiones de la página para
que la cantidad del papel usado sea mínima?
10) Una hoja de volante debe contener 50 pulgadas cuadradas de material escrito, con un margen
superior e inferior de 2 cm y otro a cada lado de 1 cm. Calcula las dimensiones de la hoja que
requiere la menor cantidad de papel.
11) Calcula las dimensiones de la caja con mayor volumen que se puede construir de una pieza
cuadrada de cartón de 100 centímetros de lado cortando cuadrados iguales de cada esquina y
doblando hacia arriba para obtener las otras caras de la caja.
12) Calcula las dimensiones de la caja con mayor volumen que se puede construir de una pieza
rectangular de cartón de 120 cm × 150 cm cortando cuadrados iguales de cada esquina y
doblando hacia arriba para obtener las otras caras de la caja.
13) Se requiere fabricar una lata cilíndrica para almacenar 20 L de aceite. Encontrar las dimensiones
que minimizan el costo del metal requerido para hacer el envase. Nota: 1 L = 1 000 cm3 =
1 dm3 .
14) Encuentra el volumen máximo que puede tener un cilindro circular recto para que ocupe 10
m2 de lámina en su construcción.
15) Se hace una caja abierta de una hoja metálica rectangular de 32 × 60 centímetros cuadrados,
cortando de cada esquina cuadrados iguales y pegando hacia arriba para obtener las otras caras
de la caja. Calcula las dimensiones de la caja con mayor volumen que se puede construir.
16) Se va a construir una ventana en forma de rectángulo coronado por un semicírculo cuyo
diámetro es igual al ancho del rectángulo. Si el perímetro de la ventana es 6 metros, ¿qué
dimensiones admitirán la mayor iluminación?
Efraín Soto A.
www.aprendematematicas.org.mx
2
17) Se necesita una caja sin tapa con una capacidad de 2 500 cm3 . El largo de la caja debe ser
el triple del ancho. Calcula las dimensiones de la caja que requieren la menor cantidad de
material.
18) Encuentra el punto de la parábola 4 y = x2 que está más próximo al punto P(0, 4).
19) Encuentra los puntos de la elipse 5 x2 + 9 y2 = 45 que están más cerca del punto P(3, 0).
20) Encuentra el área máxima de un rectángulo inscrito en un semicírculo de radio r = 10 cm.
21) Se va a construir un embalaje con tapa para naranjas para contener 12 m3 . Se va a dividir en dos
partes mediante una separación paralela a sus extremos cuadrados. Encuentra las dimensiones
del embalaje que requiere la menor cantidad de material.
22) Se va a construir un calentador para agua en forma de un cilindro circular recto con eje vertical,
usando para ello una base de cobre y lados de hojalata. Si el cobre cuesta 5 veces lo que vale
la hojalata, calcule la razón de la altura h al radio r que hará que el costo sea mínimo cuando
el volumen V es constante.
23) Un triángulo tiene dos de sus lados de longitudes a y b y un ángulo γ comprendido entre ellos.
Determine el valor de γ para que el área del triángulo sea máxima.
√
24) Demuestra que el mayor posible valor de sin θ − cos θ es 2.
Sugerencia: Los valores de | sin θ | y | cos θ | se hacen iguales cuando θ = 45, 135, 225 y 315
grados.
Efraín Soto A.
www.aprendematematicas.org.mx