1. No category

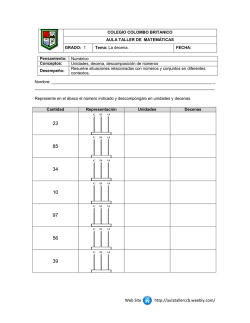
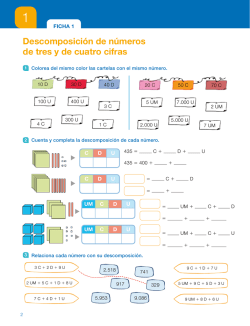
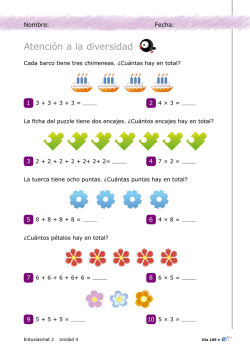
TALLER: ABN. UNAS MATEMÁTICAS MÁS SENCILLAS Y DIVERTIDAS.
AUTORES: José López Ramos y Germán Luengo Soria.
NIVEL EDUCATIVO: Primaria.
El Método ABN, Algoritmos Basados en Números, es una metodología creada por D. Jaime
Martínez Montero.
Según su creador, este método no sólo facilita la adquisición del cálculo mental, si no que te enseña
a juntar, a quitar, a repartir, …Te facilita la labor de realizar las operaciones dando el sentido
numérico que en el método tradicional no existe.
Cuatro son los pilares básicos:
- ENTENDER LO QUE SE HACE
•Se trata de que en todo momento los niños sean capaces de entender lo que hacen. Esto facilitará
que vayan llegando progresivamente a la abstracción matemática de los procesos.
- SER FIEL A LOS SISTEMAS Y MÉTODOS DE CÁLCULO
•Se intenta que trabajen los algoritmos de la misma forma.
TRABAJAR CON REFERENTES
•Los niños y niñas deben trabajar con cosas que puedan entender, por eso es necesario el uso de
objetos concretos, como palillos, tapones, pinzas... o cualquier cosa que se nos ocurra. Los
problemas que les planteemos siempre deben ser reales para ellos.
- CÁLCULO ABIERTO
•Se les ofrece un formato de cálculo para que cada uno lo resuelva como mejor sepa. Esto facilita
que pueda realizar el cálculo sea cual sea su nivel de progreso en el aprendizaje. Así mismo, permite
que se puedan dar más pasos para llegar a la solución.
•También se llama abierto, porque ofrece diversas alternativas en las operaciones o procesos que
puede usar para realizar los cálculos.
•Muchas son las ventajas que aporta este método, pero en boca de su creador, D. Jaime Martínez
Montero, señalamos las siguientes:
- Mayor motivación por parte del alumnado así como una actitud más receptiva y favorable.
- Los niños/as aprenden más rápido y mejor.
- Mayor capacidad para la resolución de problemas.
- Los niños/as van resolviendo las operaciones según su nivel de aprendizaje.
- Y como colofón, una mejora espectacular en el cálculo mental y en el nivel de autoestima de
nuestro alumnado.
El Algoritmo ABN trata a los números como son y estos constituyen el pilar fundamental de este
método, ya que antes de empezar con las operaciones hay que asentar muy bien la numeración. Las
unidades son unidades, las decenas son decenas, las centenas son centenas, etc… Y por supuesto, no
existen las llevadas. Eso de 7 + 5 son 12 y me llevo 1, y ese 1 se lo doy a las decenas, que las trato
como otras unidades, y así sucesivamente, como que no lo vemos...
Para llegar a las operaciones básicas de cálculo, hay que recorrer un camino que es fundamental que
se inicie en infantil. Este camino es la numeración. Durante esta etapa, se trabaja mucho la manipulación de objetos. Los que más usamos son los palillos, tapones o los bastoncitos de algodón. Con
ellos aprenden los números y forman sus decenas uniéndolas con gomas. O la recta numérica en paneles de goma eva donde aprenden a sumar y restar sin darse cuenta.
En 1º de Primaria seguimos trabajando durante todo el primer trimestre la numeración iniciada en
Infantil: recta numérica, amigos del 10, tabla de la suma, tabla del 100, los vecinos de un número
dado, los crucinúmeros, dobles, mitades, etc… y la descomposición. Todo es importante, pero consideramos que la descomposición es un pilar fundamental para la adquisición del esquema mental
que es el paso previo al cálculo mental. Aquí es donde tratamos a los números como números y no
como simple cifras. Por ejemplo el número 782 es 7C + 8D + 2U. Eso está claro, pero también es
6C + 18D + 2U ó 4C + 28D + 102U, y así hasta un sin fin de descomposiciones. El alumnado que
no trabaje este tipo de descomposición, si se le pregunta cuántas decenas hay en el número 782 nos
dirá que 8. El 8 ocupa el lugar de las decenas y podría haber ocupado otro lugar. Sin embargo, nuestro alumnado respondería que hay 78D. Por consiguiente, la numeración es fundamental trabajarla
mucho, y que se domine, para pasar al cálculo.
En el método tradicional se empiezan las operaciones por la derecha, es decir, se operan primero las
unidades, después las decenas y así sucesivamente, sin diferenciar las unidades de las decenas ni de
las centenas…En el Método ABN se empieza a operar por la izquierda y a cada número se le da su
verdadero valor. Si sumamos 546 + 389 lo haremos descomponiéndolo: 500 + 300, 40 + 80 y 6 +
9= 800 + 120 + 15= 935. Podemos comprobar que al realizar la suma de esta manera no hay
llevadas. Pero para llegar a este razonamiento hay que trabajar mucho con la manipulación. Siempre
pedimos materiales baratos o reciclados. Lo más económico y accesible a las familias son los
palillos y las bandejas de corcho blanco (las de la alimentación). En ellas, se trabaja la numeración
y después las operaciones, las cuales se van apuntando en unas rejillas hechas en el cuaderno.
Iniciación al método.
Antes de iniciarse en los algoritmos, hay que realizar ejercicios de numeración como son los
siguientes:
•Complementos del 10
•Recta numérica
•Iniciación a la numeración con apoyo de la recta numérica
•Centenas, decenas y unidades con palillos
•Actividades con decenas
•Complementos del 100
•Decoración de números
•Decoración con decenas completas
•Composición a partir de Unidades y Decenas
•Unidades, decenas y centenas integradas en un número
•Descomposición de un número según las unidades que lo constituyen (hasta decenas)
•Descomposición de un número según las unidades que lo constituyen (hasta centenas)
SUMA
RESTA
MULTIPLICACIÓN
C Ó M O R E A LIZA R E L P R O D U C T O
A B N P O R 2 C IF R A S
La mayoría del alumnado utilizan la opción A para el producto de dos cifras en la cual
sólo descomponen el 1er factor (en el ejemplo el número 32). Aquellos que aún no dominan
la multiplicación en sus inicios descomponen ambos factores, como en la opción B.
1º D esco m pó n
e l 1 er n ú m e r o
2 º R e a liz a e l p r o d u c to
d e la 1 ª lín e a
32 x 14
d e la 2 ª lín e a
30
2
2
10
30
420
1º D e s c o m p o n a m b o s n ú m e ro s
32 x 14
2
30
2
2
30
4
300 +120 = 420
30
2
S u m a a m b o s n ú m e ro s
10
30
10
4
300
120
6º
120
8
420
S u m a la ú ltim a c o lu m n a
4
30
300 120
420
20 + 8 = 28
300
20
2
10
4
300
20
120
8
420
+
28
=
2
448
4 º R e a liz a e l p ro d u c to d e la 2 ª lín e a
10
4
2
5º
2
2 º R e a liz a e l p r o d u c to d e la 1 ª lín e a
30
10
14
420
+
28
30
420
28
4
S u m a a m b o s n ú m e ro s
S um am os
a m b o s n ú m e ro s
=
30
4º
14
14
14
3º
3 º H a z e l p r o d u c to
448
actiludis.com
DIVISIÓN