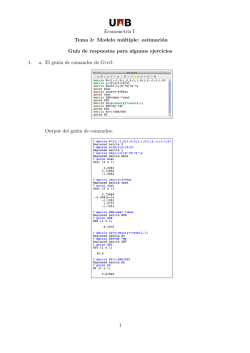
1 Vamos a realizar el ejercicio con la aplicación: Gretl, para ello lo
Vamos a realizar el ejercicio con la aplicación: Gretl, para ello lo primero es importar los datos del ejercicio que están en el archivo de excel: Pract_1_datos.xls: Se abre un cuadro de dialogo en el que tenemos que buscar el directorio donde se encuentren los datos y seleccionar de él el archivo de excel "Pract_1_datos.xls". Antes de importar el archivo debemos abrirlo en excel para saber cuántas variables y número de observaciones hay, para saber si las variables tienen puesto el nombre, y si hay o no referencia al periodo o como en este caso al individuo al que se refieren los datos. En nuestro archivo de excel tenemos 10 columnas con datos. LA primera es un contador de individuos, de 1 a 177. En la primera fila tenemos puesto en nombre de las variables. Por tanto podemos importar diciéndole a gretl que lo haga desde la columna y la fila 1: Nos dice gretl que interpreta los datos como de sección cruzada pero que si queremos darle interpretación de serie temporal que le digamos que "sí". En nuestro caso la muestra son individuos para los que tenemos información de la variable endógena y de las explicativas, o sea que le decimos "no". A).- ( 2 punto) Estimar por MCO el siguiente modelo suponiendo que cumple todas las hipótesis básica (Objeto: EQ01)y escriba la recta de regresión muestral: 1 Lo que me permite escribir la recta de regresión muestral: 2 Salaryi = 619.8 + 0.0196salesi + 0.3410 profitsi + 13.2968ceoteni La Suma Residual lo da directamente gretl debajo de la estimación. SR= 49032750 El coeficiente de determinación y el corregido también da directamente gretl debajo de la estimación. 2 R2.= 0.193089... R =0.179096 2 Para obtener la Suma Total y la Explicada Debemos operar conocidos R . y SR SR 49032750 ⇒ ST = = = 60765996.3 ST 1 − R 2 1 − 0.193089 SE = ST − SR = 11733245.3 R2 = 1 − También podríamos haberle pedido a Gretl que nos de la SE, SR y ST, eso se hace desde el menú de la ecuación estimada, en Análisis, ANOVA: En el cuadro, Suma de cuadrados de la regresión es la SE, suma de cuadrados del residuo es la SR y suma de cuadrados de total es la ST. Además, debajo nos da el cálculo del coeficiente de determinación y la F del Análisis de la Varianza. Interpretación del coeficiente de la variable sales: …Por cada millón de dólares que aumenten las ventas de la empresa, el sueldo del individuo aumentará en 19.6 dólares Interpretación del coeficiente de la variable Ceoten: Por cada año adicional de director ejecutivo en la empresa el salario aumenta en 1326.8 dólares 3 Manteniendo los demás factores constantes (en cada caso). B.- (2 puntos) Contraste la significatividad individual de las siguientes variables al 1 al 5 y al 10%: A partir del cuadro de la estimación anterior: Podemos ver en la última columna el p-valor: probabilidad de que el estadístico tome ese valor si la hipótesis de no significatividad fuera cierta. Cuanto más próximo a cero menos credibilidad tiene la hipótesis nula. Cuanto más pequeño podremos rechazar la hipótesis nula a un nivel de significación menor. Al lado del p-valor tenemos unas estrellas que nos están indicando a que nivel de significación menor de entre el 1% (***), el 5% (**) y el 10% (*) podemos rechazar la hipótesis nula. Como vemos, que la constante no sea significativa podemos rechazarlo incluso al 1%; Los parámetros que acompañan a beneficios y el número de años de experiencia en dirección concluimos que son significativos (rechazamos la Ho) si consideramos que la hipótesis no es cierta a partir de un p-valor inferior al 5%. Mientras que para rechazar la hipótesis nula de que las ventas no afectan al salario debemos utilizar un nivel de significación superior al 7.51% por ejemplo al 10% Objeto: EQ01 constante Sales Profits ceoten estadísticConclusión H0 9.46 Rechazo no significatividad ∀ ε 1.79 Rechazo no signif ∀ ε > 7'51% 2.07 Rechazo no signif ∀ ε > 4'02% 2.36 Rechazo no signif ∀ ε > 1'94% β1=0 β2=0 β3=0 β4=0 C.- (4 puntos) Contraste al 5% de nivel de significación las siguientes hipótesis nulas: Objeto: Estadístico de contraste 2 ⎛ βˆ − 1 ⎞ ⎛ 0.341 − 1 ⎞ 2 ⎟ = F =t =⎜ 3 =15.95397 ⎜ σˆ ˆ ⎟ ⎜⎝ 0.1649 ⎟⎠ ⎝ β3 ⎠ Distribución p-valor F(1, 177-4) P < 0.0001 2 Objeto: HIP_1 H 0 : β3 =1 Para contrastar desde el menú del modelo, elijo las opciones "contrastes" y "restricciones lineales". 4 Después escribo la restricción en el cuadro de dialogo: Y el resultado lo muestra en el siguiente cuadro que se completa con la estimación del modelo restringido. A nosotros nos interesa el resultado del estadístico F=15.95 con un p valor inferior al 1% por lo que rechazamos la hipótesis nula prácticamente para cualquier nivel de significación. Guardamos esta salida como un icono y le cambiamos el nombre a HIP_1 Para contrastar la Hip_2 usamos el resultado obtenido en Hip_1 porque la hipótesis nula es la misma. La diferencia radica en que éste es un contraste de una sola cola, por lo que tenemos que utilizar el estadístico t, y acumular el nivel de significación en un solo extremo de la distribución: t(177-4) -t0.05(177-4) = βˆ − 1 t= F = Objeto: HIP_2 H 0 : β3 = 1 H A : β3 < 1 = -3.9942 3 σˆ βˆ -1.64 3 Conclusión: -3.99 < -1.64 Por lo que rechazamos la hipótesis nula. Para el resto de las hipótesis procedemos de la misma manera que en el primer contraste Objeto: HIP_3 F=18.50838 F(2, 177-4) P-valor=0 5 H 0 : β 2 = β3 = 0 Conclusión y interpretación económico del resultado del contraste: Rechazamo hipótesis nula a cualquier nivel de significación p > 5.20023*10-8 Salida de gretl: Conjunto de restricciones 1: b[SALES] = 0 2: b[PROFITS] = 0 Estadístico de contraste: F(2, 173) = 18.5084, con valor p = 5.20023e-008 Objeto: HIP_4 F=127.3998 F(4,173) P=0 H0: sign. conjunta de todos los parámetros de posición Conclusión y interpretación económica del resultado del contraste: Rechazamos la hipótes F=86.55659 F(3,173) Objeto: HIP_5 H 0 : β1 = β 2 = β 3 = β 4 Conclusión y interpretación económica del resultado del contraste: P=0 rechazamos la H0 Estadístico de contraste: F(3, 173) = 86.5566, con valor p = 2.99959e-034 F=5.8751 F(1,173 Objeto: HIP_6 H 0 : β3 + β 4 = 0 Conclusión y interpretación económica del resultado del contraste: Al 5% rechazo la Ho pero al 1% acepto. Objeto: HIP_7 F=13.79925 P=0.016 F(3,173) p=0 H0: Análisis de la varianza D.- Obtenga el gráfico de los residuos y comente si cree que cumplen las hipótesis deseadas. Desde el menú de la ecuación: 6 No ofrece el correlograma de los residuos porque es un modelo de corte transversal. E. Obtenga las correlaciones entre las variables explicativas del modelo e indique a qué hipótesis de las asumidas en el MLG afectan. Desde el menú de la pantalla inicial, "ver", "matriz de correlaciones" Obtenemos: CEOTEN SALES PROFITS CEOTEN 1.0000 SALES -0.0677 1.0000 PROFITS -0.0216 0.7983 1.0000 Las variables: Beneficio y Ventas están corrrelacionadas casi en un 80%. Afecta a la hipótesis de no multicolinealidad. Aunque no exista multicolinealidad exacta (100%) sí que hay aproximada por el alto grado de correlación entre estas variables. F. Dado el MLG anterior obtenga mediante dos métodos alternativos el valor del estadístico F para realizar el contraste la siguiente hipótesis nula: H 0 : β 2 = β 3 = 0 . - Mediante restricción utilizando el estadístico ( Rβˆ − C )'[ R ( X ' X ) −1 R' ]−1 ( Rβˆ − C ) ~ F (r , T − k ) F= rσˆ 2 ⎛0⎞ ⎛ 0 1 0 0⎞ ⎟⎟ C = ⎜⎜ ⎟⎟ r = 2 . ⎝0⎠ ⎝ 0 0 1 0⎠ donde R = ⎜⎜ 7 - Mediante diferencia de SR. Cuando anteriormente hemos realizado el contraste de hipótesis HIP_3, hemos obtenido este resultado: En la parte baja del cuadro aparece el modelo estimado bajo la restricción, el modelo restringido, es decir Salaryi = γ 1 + γ 2 ceoteni + ui Para obtener la SR de ese modelo restringido a partir de la desviación típica MCO estimada de los residuos: σˆ 2 = SR T −k → SR=583'2142 ⋅ (177 − 2) = 59.524.271 SRmodelo_1~mod Amplio..= 49032750 (El modelo de partida) SRmodelo_2~mod.restringido.= 59524271 F= SRR − SRA T − k A 59524271 − 49032750 177 − 4 ⋅ = ⋅ = 18 '5083 SRA r 49032750 2 También se puede calcular con los dos modelos estimados a partir del R2: (Habría que estimar el modelo restringido para obtener el valor del R2). R 2 A − R 2 R T − k A 0.193089 − 0.020434 177 − 4 F= ⋅ = ⋅ = 18.5064 2 r (1 − 0.193089) 2 (1 − R A ) Se compara con una F(2, 173) al nivel se significación fijado. Aunque ya hemos visto en el contraste Hipo_3 que este estadístico tiene un p-valor asociado de 0%. 8
© Copyright 2026