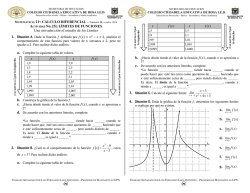
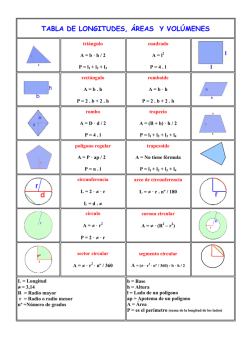
Manual de referencia mysql 5 5
SECRETARIA DE EDUCACION SECRETARIA DE EDUCACION COLEGIO CIUDADELA EDUCATIVA DE BOSA I.E.D. COLEGIO CIUDADELA EDUCATIVA DE BOSA I.E.D. Educación en Pre-escolar – Básica – Secundaria y Media Académica Educación en Pre-escolar – Básica – Secundaria y Media Académica MATEMÁTICAS 11º: DÍA DE LA MATEMÁTICA – septiembre 30 de 2014 EL ARTE EN LAS MATEMÁTICAS: EL TANGRAM & LOS MOVIMIENTOS EN EL PLANO PRIMER MOMENTO: Lectura sobre el origen e historia del Tangram El Tangram es un juego chino muy antiguo, consistente en formar siluetas de figuras con las siete piezas dadas sin solaparlas. Las siete piezas, llamadas “Tans”, son: cinco triángulos de diferentes tamaños, un cuadrado y un paralelogramo. Existen varias versiones sobre el origen de la palabra Tangram. Una de las más aceptadas cuenta que la palabra la inventó un inglés uniendo el vocablo cantonés “tang” que significa chino, con el vocablo latino “gram” que significa escrito o gráfico. Otra versión dice que el origen del juego se remonta a los años 618 a 907 d.C., época en la que reinó en China la dinastía Tang de donde se derivaría su nombre. Hay una leyenda que dice que un sirviente de un emperador Chino llevaba un mosaico de cerámica, muy caro y frágil, y tropezó rompiéndolo en pedazos. Desesperado, el sirviente trato de formar de nuevo el mosaico en forma cuadrada pero no pudo. Sin embargo, se dio cuenta de que podía formar muchas otras figuras con los pedazos. SEGUNDO MOMENTO: Lectura y estudio los movimientos o transformaciones en el plano La palabra transformación implica que un objeto cambia de alguna manera. En las transformaciones en el plano se deben tener en cuenta tres aspectos: La figura original. Una regla u operación que describa el cambio. La figura que resulta después del cambio. Los tres movimientos o transformaciones en el plano son: traslación, rotación y reflexión. Cada uno de ellos se explica brevemente a continuación. TRASLACIÓN Una traslación es el movimiento de cada punto de un plano a otro punto en el mismo plano, por medio de un vector que indica una distancia, una dirección y un sentido. Ejemplo: Al trasladar el polígono el vector se obtiene el polígono ROTACIÓN Una rotación es el movimiento de cada punto de un plano a otro punto en el mismo plano, siguiendo la trayectoria de un arco de alguna circunferencia con centro un punto fijo dado, y uno de dos sentidos: de las manecillas del reloj ( ) o contrario a estas ( ). El centro de la circunferencia se llama el centro de rotación. Ejemplo: Al rotar el polígono según la rotación º que significa: “rotar el polígono 60º, con centro de rotación el punto , en sentido contrario a las manecillas del reloj”, se obtiene el polígono . REFLEXIÓN Una reflexión respecto a una recta , denominada eje de reflexión, es el movimiento que a cada punto del plano le asigna otro punto del mismo plano, tal que el segmento es perpendicular a la recta , y los puntos y están a la misma distancia de . Ejemplo: Al reflejar el polígono con respecto a la recta , se obtiene el polígono . TERCER MOMENTO: Construcción del Tangram 1. En una hoja cuadriculada, dibuje un cuadrado 12 cm. Luego, divida el cuadrado de manera que se obtenga una rejilla compuesta por cuadrados de 3 cm. (Ver Figura 1) 2. Trace cada uno de los segmentos que se muestran en la Figura 2. Estos segmentos determinan el Tangram. 3. Copie tres veces el Tangram construido en uno de los octavos de cartulina (Figura 3). ¡Importante! Cada integrante debe elaborar tres Tangram. según . Figura 1 TRABAJO PREPARADO POR LUIS FERNANDO LARA QUINTERO – PROFESOR DE MATEMÁTICAS UPN Figura 2 Figura 3 TRABAJO PREPARADO POR LUIS FERNANDO LARA QUINTERO – PROFESOR DE MATEMÁTICAS UPN SECRETARIA DE EDUCACION SECRETARIA DE EDUCACION COLEGIO CIUDADELA EDUCATIVA DE BOSA I.E.D. COLEGIO CIUDADELA EDUCATIVA DE BOSA I.E.D. Educación en Pre-escolar – Básica – Secundaria y Media Académica Educación en Pre-escolar – Básica – Secundaria y Media Académica CUARTO MOMENTO… ¡de ser creativos! ANEXO Cada uno de los integrantes del grupo, conformado por tres estudiantes, debe realizar lo siguiente: 1. Elegir una figura distinta de las que aparecen en el ANEXO. 2. Construir la figura seleccionada con los tres Tangram que elaboró individualmente. 3. Elegir uno de los tres movimientos en el plano (traslación, rotación o reflexión). 4. Pegar cuidadosamente las tres figuras en el otro octavo de cartulina de manera que se pueda visualizar uno de los tres movimientos en el plano (traslación, rotación o reflexión), o dos de ellos. Ejemplo: Al pegar en la cartulina la construcción de la Figura 4, se debe hacer como se muestra en la Figura 5. Figura 4 Figura 5 A continuación se muestra la Figura 5 aplicando los movimientos en el plano. Traslación Rotación Reflexión Traslación y Reflexión TRABAJO PREPARADO POR LUIS FERNANDO LARA QUINTERO – PROFESOR DE MATEMÁTICAS UPN TRABAJO PREPARADO POR LUIS FERNANDO LARA QUINTERO – PROFESOR DE MATEMÁTICAS UPN
© Copyright 2026