1. Educación

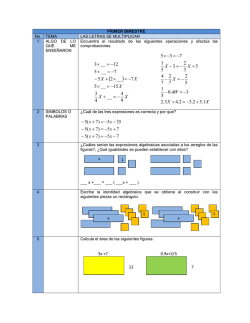
Instituto Alexander Dul
Secundaria Clave: ES4-617
Guía de estudio tercer periodo
Asignatura: Matemáticas III
Nombre del alumno (a):
Docente Titular: Mario Alamilla Velázquez.
Grupo: 3° A
Fecha:
febrero 2015
Instrucciones generales: Después de leer con mucha atención las preguntas contéstalas siguiendo las instrucciones
de cada bloque, escriba de manera legible y ordenada, utilizando lápiz, asimismo evitando hacer correcciones.
I.
Teorema de Pitágoras.
1.
Utilizando el teorema de Pitágoras resuelva los siguientes problemas
a. Para sostener la torre de una estación de radio de 72 metros de altura, se desean poner tirantes de 120
metros para darle mayor estabilidad. Si se proyecta tender los tirantes desde la parte más alta de la torre,
¿a qué distancia del pie de esta deben de construirse las bases para fijar dichos tirantes?
C
120 m
72m
B
A
x
b. La base a que se sujeta la cadena que sirve para el puente levadizo de la torre de un castillo, está situada a 36 m.
Del pie de la misma. Calcular la longitud de la cadena, si esta se fija en la torre a 48 m. Que es su parte más alta.
c
X=
48 m.
A
36 m
B
1
II.
Funciones cuadráticas o de segundo grado
1.
Contestar las siguientes preguntas.
a. ¿Una función en la que la variable independiente esta elevada al cuadrado se llama?
2
b. ¿A las ecuaciones de segundo grado de la forma general ax  bx  0 , en donde se desconoce el
término independiente se llama?
2
c. ¿A las ecuaciones de segundo grado de la forma general ax  c  0 , en donde se desconoce el
término independiente se llama?
d. La grafica de las funciones cuadráticas se llama?
2.
Trazar la grafica de las funciones cuadráticas siguientes
a)
x
y  x2 - 6x  5
y
PARES ORDENADOS
-1
0
1
2
3
4
5
6
7
2
b)
x
y  - x 2  2x  8
y
Pares Ordenados
-3
-2
-1
0
1
2
3
4
5
c)
x
y  x 2 - 6x  9
y
Pares Ordenados
0
1
2
3
4
5
6
3
I.
Ecuaciones de segundo grado
I.
Resolver las siguientes ecuaciones incompletas de segundo grado de la forma ax 2 + bx = 0 ó bien de la
forma ax2 + c = 0, comprobando las soluciones.
2.
a)
4x
b)
- 3x
c)
3x
d)
2x
2
2
2
2
 1 2 x 0
c o m p ro b aocn
i
 2 7 x 0
c o m p ro b aocn
i
- 75 0
c o m p ro b aocn
i
- 27 0
c o m p ro b aocn
i
Resolver las siguientes ecuaciones completas de segundo grado utilizando el método indicado para cada
una de ellas, comprobando las soluciones.
Por factorizacion
a)
a)
x 2  2x - 24  0
com probacion
x 2  16x - 32  0
com probacion
4
Por el metodo de completar cuadrados
a)
x 2  5x - 14  0
com probacin
a)
x 2  7x  6  0
com probacion
Utilizando la form ulageneral
I.
d)
3x 2 - 5x  2  0
com probacion
E)
x 2  2x  24  0
com probacion
Con los datos que se dan a continuación, calcular el rango, intervalos, amplitud de clase, crear: tabla de frecuencias,
grafica de barras y grafica poligonal, determinar la moda mediana y media aritmética así como la tabla y grafica de
sectores circulares correspondiente.
Para determina el peso medio de los 60 trabajadores de una fábrica, se investigo el peso de cada trabajador,
registrándose los siguientes datos, mismos que están expresados en kilogramos y ordenados de menor a mayor
52
63
67
73
81
52
63
67
74
82
53
63
68
75
83
54
63
69
75
84
55
64
70
75
85
57
64
70
76
86
58
65
70
76
87
59
65
70
77
88
60
65
71
78
89
61
66
7I
79
90
61
66
71
80
92
62
67
72
80
93
5
Rango =
Intervalo =
Amplitud de clase =
a)
TABLA DE FRECUENCIAS.
PESO DE 48 TRABAJADORES DE UNA FABRICA, EXPRESADO EN KILOGRAMOS
Amplitud
de clase
Frecuencias
Puntos medios
productos
totales
Moda =
Mediana =
Media aritmética =
b)
TABLA DE SECTORES CIRCULARES.
ESTATURA DE 50 TRABAJADORES DE FERREMEX, EXPRESADOS EN CENTIMETROS
Amplitud
de clase
totales
Frecuencias
Por ciento %
Grados
Grafica de barras:
Grafica poligonal:
Nota: para realizar las graficas utiliza equipo de geometría y colores.
GRAFICA DE SECTORES CIRCULARES O DE PASTEL
ARQ. MARIO ALAMILLA VELÁZQUEZ
DR. RAFAEL DULIJH URANGA HERNANDEZ
DIRECTOR GENERAL
6