1. Ingeniería

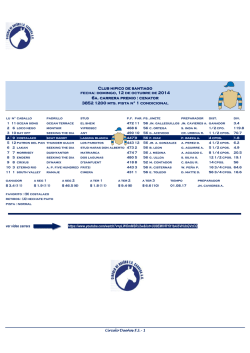
Rev. 1.0
An Introduction to Radio Waves Propagation: Generic Terms,
Indoor Propagation and Practical Approaches to Path Loss
Calculations, Including Examples
By Adi Shamir1
Abstract: Estimating propagation path loss is required in order to predict the
performance of a wireless system in its working environment. Free-space propagation
loss calculation is explained. An empirical model is suggested for indoor path loss
prediction. Theoretical calculation of reflection and transmission coefficients of
electromagnetic waves from dielectric medium is shown as a tool for prediction of
reflection and transmission losses. Simulative calculation is presented for
demonstrating prediction of propagation loss through finite thickness walls.
Simulation of the ‘2 ray model’ is presented to demonstrate the effect of antenna height
on propagation loss, as an example of the ‘dominant path’ approach. Examples and
simulations are given for a working frequency of 2.4GHz
1 Introduction
Most wireless application designers are commonly interested in the basic questions of
‘what is the maximum distance for which the wireless channel is going to work’, or ‘is
there going to be a communication link between 2 stations, if I place one here and
another there…’. Unfortunately, answering these sorts of questions is not as easy as
asking them. The simplest approach towards answering the above questions, is by
comparing 2 things: a) the dynamic range of the system in hand, and b) the
electromagnetic waves propagation loss.
The dynamic range is a characteristic of the system that is well known to the designer. It
determines the maximum power loss that is allowed throughout the communication
channel (between transmitter and receiver), while still maintaining the communication
link. The main characteristics that determine the dynamic range are the transmission
power and receiver sensitivity. For example, if a system is said to have an 80dB dynamic
range, it means that, in practice, the receiver can detect a power level 80 dB lower than
the transmission power. Accordingly, a system having a transmission power of 10dBm
can detect signals at a level not lower than –70dBm.
The propagation loss is the part of the energy that is lost throughout the propagation path.
The propagation path is the path through which the electromagnetic waves travel, from
their origin at the physical location of the transmitter, until they reach the receiver
location. For example, if at a certain path the propagation loss is 50 dB, and we have a
10dBm transmitter, the power level at the receiver will be –40dBm.
© 2002, RFWaves Ltd.
Page 1 of 21
Radio Propagation
Rev. 1.0
Although the theoretical laws of physics describe very accurately the different aspects of
electromagnetic wave propagation, it is vital to understand that the complexity of
practical life makes the actual propagation loss very difficult to predict. In an ideal ‘freespace’ scenario, the traveling wave can be described as propagating in a direct ray from
the transmitter to the receiver. However, most applications in today’s short range RF
scene operate in environments that are far different from the ideal free-space scenario.
Effects such as reflections or scattering of waves from floor, ceiling, walls, furniture and
various objects lead to a situation in which the wave arriving at the receiver location is a
result of interference between waves traveling through different paths (‘multipath
propagation’). This interference can be either constructive or destructive, resulting in an
increase or decrease of received power compared to the ideal free-space propagation.
Energy absorbing objects that exist in any of the traveling wave’s path, such as walls,
doors, and even the human body can also dramatically affect the propagation loss.
Things get even more complicated when the systems themselves are mobile, which
means that the coordinates in space of either the transmitter, receiver or both change with
time, and therefore the propagation loss constantly changes. Many numerical tools and
computational methods have been developed in order to help designers predict wave
propagation loss in various environments. Such tools usually require substantial
computational and financial resources. In many cases though, it is quite sufficient for the
designer to use very simple models for propagation loss prediction. Such models will be
described in detail in this article.
2 Free-Space Propagation
As noted before, when an electromagnetic wave travels in free space, its path is described
as a direct ray connecting the transmitter and receiver. In order to calculate the free-space
propagation loss, it is possible to use the Ferris Transmission equation:
P
 λ 
(2.1) r = g t ⋅ g r ⋅ 

Pt
 4πR 
2
Where: Pr is the received power, Pt is the transmitted power, gt and gr are the gain values
of the transmitting and receiving antennas, respectively, and R is the physical distance
between the transmitter and the receiver. The power in this model drops as the inverse
square of the distance between the transmitter and the receiver; so, for example, when the
distance increases by a factor of 2, the received power drops by 4.
Equation 2.1 can be transformed into its more familiar form in a logarithmic scale, and
the propagation loss in dB units can be written as:
 R
 4πR 
(2.2) PL = −Gr − Gt + 20 log
 = Gr + Gt + 22 + 20 log 
λ
 λ 
© 2002, RFWaves Ltd.
Page 2 of 21
Radio Propagation
Rev. 1.0
Where Gr and Gt are the receiving and transmitting antenna gain values in dB,
respectively, R is the distance between the transmitter and the receiver, and λ is the
wavelength.
Applying a wavelength of 12.3 cm (frequency = 2.44GHz) to Equation 2.2 yields:
(2.3) PL2.44 = −Gr − Gt + 40.2 + 20 log( R)
Where R is the distance in meters.
Figure 2-1: Free-space Propagation Loss at 2.44GHz, shows the propagation loss in free
space at a frequency of 2.44GHz assuming 0dBi antennas on both sides of the channel.
(Gr = Gt=0).
It can be seen in Figure 2-1: Free-space Propagation Loss at 2.44GHz that 40.2 dB of
power are lost over the first meter. Whenever the distance increases by a factor of 10, 20
dB more of power are lost. Whenever the dynamic range of a system is given, Equation
2.3 can be solved for R and the maximum distance can be calculated. For example, a
2.44GHz system with a dynamic range of 80dB and zero dBi antennas can reach a
distance of about 79[m] in free space.
Figure 2-1: Free-space Propagation Loss at 2.44GHz
© 2002, RFWaves Ltd.
Page 3 of 21
Radio Propagation
Rev. 1.0
It is important to note that the antenna gain is a directive property of the antenna, and
must be determined according to the orientation of the antennas in space relative to the
direction of propagation, when applying the above equations.
It is also important to note that this model assumes that the antennas are polarizationmatched. Meaning, that there are no losses due to difference in antenna polarization. If
the antennas are not polarization-matched, another loss factor has to be added to the
equation. Generally, for an ideally linearly polarized antennas, the polarization loss is
proportional to the square of the cosine of the angle between both polarization directions.
So, for example, if 2 dipole antennas are placed at an angle of 45 degrees relative to each
other, the polarization loss factor is around –3dB.
The free-space propagation model is only a good approximation of real propagation loss
in cases where the receiving and the transmitting antennas are close enough to each other,
so that the distance between them is much smaller than the distance to any reflecting
object. For instance, in an outdoor environment, it will be accurate only when the
antennas are closer to each other than their height above the ground, so that the wave
reflected from the ground loses its significance and does not interfere with the direct
wave. When this is not the case, different models need to be applied, as will be explained
in the following sections.
3 Indoor Propagation
In today’s short range RF scene, many applications are targeted to operate in an indoor
environment, such as residential homes or office buildings. As mentioned before,
predicting propagation loss in such environments is very complicated. The main problem
with numerical simulation tools used for that purpose, besides the financial and
computational resources they require, is the fact that they are capable of simulating only
specific site scenarios. They require, as part of the input data, a physical description of
the site and the results, although being very accurate, will apply only to that site, and each
time only to one position of the transmitter and receiver. Therefore, a more general and
simple method of modeling is required.
The most common method of predicting indoor propagation loss is by using empirical
models. The empirical model is based on actual measurements made in a typical
environment, that is similar to the one in which the system is commonly needed to
operate. In practice, a transmitter and receiver are placed at various locations in the
environment, at various distances apart, and the power loss is measured. A large amount
of data is collected, and the power loss is plotted as a function of the distance between the
transmitter and the receiver. Numerical curve fitting is then performed over the sampled
points.
The average behavior usually indicates that the power drops at a much higher rate than it
does for the free-space propagation model. Whereas in the free-space model the power
drops as the inverse square of the distance, the indoor empirical models show that the
© 2002, RFWaves Ltd.
Page 4 of 21
Radio Propagation
Rev. 1.0
power in an indoor environment drops by a power of about 3 to 4 of the distance. The
reason for that is destructive interference caused by various waves traveling through
different paths to reach the receiving antenna, plus losses due to those waves
encountering various objects in their paths. For example, a direct wave, a wave reflected
from the floor, a wave reflected from the ceiling, waves reflected from walls and
furniture, a wave propagating through a wall, etc.
Figure 3-1: Indoor Propagation Loss in 2.4GHz – Experimental Result shows the result of
an experiment performed in the RFWaves office in Israel. The inner walls of the office
are made of gypsum boards. The transmitting and receiving antennas were placed at
various locations in the office, at a height of 1 meter above the ground, and the power
loss was measured. The frequency on which the measurements were made was 2.4GHz.
The results were plotted as a function of the logarithm of the distance between the
transmitter and the receiver. A linear fit using the minimal squares method was
performed over the results and yielded the following approximation for the propagation
loss in dB:
(3.1) PLindoor − 2.4 ghz = 40 + 31log( R) ± 8
Where R is the distance in meters between the transmitter and the receiver.
As was the case for the free-space formula (Equation 2.3), when the dynamic range is
known, Equation 3.1 can be solved for R and will yield the maximum distance for the
system in an indoor environment similar to the one in which this experiment was made.
It can be seen from Figure 3-1: Indoor Propagation Loss in 2.4GHz – Experimental
Result that, as in the free-space model for 2.4GHz, the first meter yields a 40 dB loss.
This is because measurements were made where the antennas height above the ground
was about 1 meter and so the free-space model is applicable. The issue of antenna height
will be discussed in detail in section 6.
However, unlike in the free-space propagation model, when we advance to a distance of
10 meters, we lose another 31 dB, which is 11 dB more than we lose at the same distance
in free-space. From a different point of view, assuming we have a system with a dynamic
range of 80 dB, solving Equation 3.1 for R shows that our systems will now operate to a
distance of about 19.5[m], whereas the result we got for the free-space model based on
Equation 2.3 was almost 80 meters!
The factor 31 in Equation 3.1 means that the power now drops with distance, at a power
of 3.1, which is much faster than in the free-space propagation model where the factor is
2. Due to the fact that this experiment can be made in different environments, with
different conditions (such as different height of the ceiling, different materials of floor
and walls, etc.) different experiments can yield different values for that factor. Numerous
values can be found in the professional literature, mostly ranging from 3 to 4.
© 2002, RFWaves Ltd.
Page 5 of 21
Path Loss
Radio Propagation
Rev. 1.0
90
85
80
75
70
65
60
55
50
45
40
1
10
100
Distance[m] - logarithmic scale
Figure 3-1: Indoor Propagation Loss in 2.4GHz – Experimental Result
The reader must have noticed the 8dB error obtained in this experiment. This is a typical
error for such models, and has to be taken into account when applying the empirical
model to obtain the value of the propagation loss. There are 3 main reasons for this
phenomenon:
Different spots in the environment where the measurements were made may indeed yield
a different result; although the distances are the same. This is because the various
propagation paths depend on the physical characteristics and architecture of the
environment in which the measurements are made.
Fading effects in space: It can be observed that a small change in the coordinates of the
receiver or transmitter in space, within fractions of a wavelength, can result in a
significant change in the received power, within a range of 10dB. This happens when
moving from ‘dead zones’, where destructive interference between propagation paths
occurs, and the received power decreases, to zones where constructive interference
occurs and the received power increases. These ‘deeps’ and ‘peaks’ are located in a
resolution of the order of magnitude of around half a wavelength. This phenomenon is
also known as ‘fast fading’ due to the high density of the variations. Figure 3-2: Fast
Fading in an Indoor Environment – Simulation shows a simulation of this kind of
behavior based on the presented indoor empirical model. The nature of this phenomenon
can be described as random fluctuations of the signal power in space around an average
value with some statistical distribution around that value.
Fading effects in time: Even when the positions of the receiver and transmitter remain
constant in space, the received signal seems to vary in time. The typical time constant for
these fluctuations is a typical human time constant (seconds), and they originate from the
dynamic nature of the environment, mainly due to human movements, opening and
closing of doors, moving vehicles etc. The human movements affect the different
propagation paths and therefore the propagation loss.
© 2002, RFWaves Ltd.
Page 6 of 21
Radio Propagation
Rev. 1.0
Figure 3-2: Fast Fading in an Indoor Environment – Simulation
To summarize this section, the empirical model for indoor propagation is a practical
approach to estimate propagation loss in an indoor environment. However, although this
method is practiced very often, it is important to remember that this is only a general
averaging approach, which may not always reflect real life.
When more accurate results are needed, numerical simulations must be made using the
specific site information. An alternative approach to simulation, is calculating the
propagation loss using the dominant path approach. This approach takes into account the
interference between the most dominant propagation paths, i.e., the ones with the
minimum propagation loss. For example, in an outdoor environment, the most dominant
paths are usually the direct path, and path of the wave reflected from the ground.
In General the superposition of the fields originating from the various dominant paths
must include the amplitude and phase of the field arriving to the receiver from each path,
as indicated by equation 3.2:
(3.2) Etotal = ∑ E n e iϕ n
n
Where the sum goes through all the dominant paths, En is the field amplitude of the wave
of path n and φn is the phase of that wave.
In order to calculate the path loss through various paths when using the dominant path
approach, it is necessary to know the propagation loss due to reflection and transmission
of waves from and through various materials. This will be explained in detail in the
following sections.
© 2002, RFWaves Ltd.
Page 7 of 21
Radio Propagation
Rev. 1.0
4 Transmission and Reflection With Dielectric Materials
A traveling electromagnetic wave that incidents a dielectric material, is partially reflected
and partially transmitted (refracted) into the dielectric medium. In accordance with the
conservation of energy, the sum of the power of the reflected and refracted waves must
be equal to the energy of the incident wave. Furthermore, an electromagnetic wave
traveling through a dielectric medium loses part of its energy due to the dissipation
caused by polarization of the dielectric material by the wave’s electric field.
Most often, when attempting to estimate propagation loss in complex environments, it is
necessary to calculate the amount of reflected or transmitted energy from or through
various objects. As indicated in the previous section, this is useful when trying to
estimate propagation loss using the dominant path approach. A common example is the
energy lost due to penetration of an electromagnetic wave through a wall, which will be
discussed in further detail in section 5. Another example is the energy of a wave reflected
from the ground on the propagation path, which will be discussed in section 6.
When estimating the reflected or transmitted energy, it is necessary to calculate the field
or power reflection and transmission coefficients. These coefficients depend on the
dielectric properties of the dielectric medium, which are defined by its dielectric constant.
This constant is usually written as a complex number (Equation 4.1), where the
imaginary part is responsible for dissipation of energy when the wave travels through the
dielectric medium.
(4.1) ε r = ε r '+iε r ' '
The imaginary part is highly frequency-dependent, and is usually much smaller than the
real part. In many cases it can be neglected in the analysis. Some dielectric constants (real
part) of common materials in an indoor scenario appear in
Table 0-1. The imaginary part for these materials is around 0.1 at the GHz scale. It is
important to mention that these values are not well defined. For example, an outer
concrete wall that is exposed to rain may have a higher dielectric constant than one that
remains dry.
Table 0-1: Dielectric Constants of Various Materials
Glass
4-10
4.1.1.1 Marble
12
Concrete
4-6
Gypsum board
3
Wood
1.5-2
Formica
4
Water
80
Ground
5-30
The reflection and transmission coefficients also depend on the angle of incidence and
polarization of the incident wave, as will be explained immediately.
© 2002, RFWaves Ltd.
Page 8 of 21
Radio Propagation
Rev. 1.0
Assuming a plane wave traveling through air (ε=1) to a planar boundary of a medium
having some dielectric constant ε (Figure 4-1). It is well known, that in order to satisfy
the boundary conditions imposed by Maxwell’s equations on the planar boundary, the
angle of reflection must be equal to the angle of incidence. In addition, Snell’s law must
also be satisfied, so that the connection between the angle of incidence and the angle of
transmission is:
(4.2) sin θ = ε sin θ T
Where θ is the angle of incidence and θT is the angle of transmission.
θ
θ
ε
θt
Figure 4-1: A Wave incidents Dielectric Medium
Remembering the fact that a traveling electromagnetic wave propagating in a certain
direction is described by electric and magnetic periodic fields, both in the same phase,
perpendicular to each other and to the direction of propagation, there are 2 possible
polarizations for the incident electric field. TE polarization (transverse electric) is when
the electric field is perpendicular to the plane of incidence (defined by the directions of
the incident, transmitted and reflected waves) and the magnetic field is parallel to it,
whereas TM polarization (transverse magnetic) is when the magnetic field is
perpendicular to the plane of incidence and the electric field is parallel to it.
In order to produce TM polarization, it is possible to place a transmitting monopole
antenna vertically to the planar boundary, whereas placing a dipole antenna parallel to the
planar boundary can produce TE polarization. Figure 4-2 shows the difference between
TE and TM polarizations.
© 2002, RFWaves Ltd.
Page 9 of 21
Radio Propagation
Rev. 1.0
TM Polarization
TE polarization
E
H
Propagation
H
Direction
Propagation
E
ε
Direction
ε
Figure 4-2: TE and TM Polarization
The reflection coefficient for TE polarization is given by the following equation:
(4.3) ΓTE =
cosθ − ε cosθ T
cosθ + ε cosθ T
The transmission coefficient for TE polarization is given by:
(4.4) TTE =
2 cosθ
cosθ + ε cosθ T
Figure 4-3: Reflection Coefficient For TE Polarization shows the reflection coefficient as
a function of the incident angle for TE polarization, and various values of the dielectric
constant.
In TM polarization, the reflection coefficient is given by:
(4.5) ΓTM =
ε cosθ − cosθ T
ε cosθ + cosθ T
And the transmission coefficient for TM polarization is given by:
(4.6) TTE =
2 ε cosθ
ε cosθ + cosθ T
Figure 4-4: Reflection Coefficient for TM Polarization shows the reflection coefficient as
a function of the incident angle for TM polarization, and various values of the dielectric
constant.
In all the above equations for the reflection and transmission coefficients (4.3-4.6) θ is
the angle of incidence, θT is the angle of transmission determined by Snell’s law
(Equation 4.2), and ε is the dielectric constant of the medium.
© 2002, RFWaves Ltd.
Page 10 of 21
Radio Propagation
Rev. 1.0
It can be seen, from the reflection coefficient at TM polarization as appears in Figure 4.4,
that there is a certain angle, where no reflection occurs. This angle is called Brewster’s
angle, and it equals:
(4.7) θ B = arctan ε
It is important to mention that the reflection coefficients presented above determine the
ratio between the amplitudes of the incident and reflected electric fields. The fraction of
the average reflected power is therefore given by the square of the reflection coefficient.
(4.8) Preflected = Pincident Γ
2
And the transmitted power is given by:
2
(4.9) 1 − Γ = ε T
2
Figure 4-3: Reflection Coefficient For TE Polarization
© 2002, RFWaves Ltd.
Page 11 of 21
Radio Propagation
Rev. 1.0
Figure 4-4: Reflection Coefficient for TM Polarization
The average fraction of reflected power in a logarithmic scale (dB units) can therefore be
derived from the reflection coefficient by:
(4.10) Γdb = 20 log Γ
This calculation can be used when calculating propagation loss due to reflection, and
added to the free-space logarithmic propagation equation (Equations 2.2-2.3). It can be
observed from the expressions for the reflection coefficients that, for a direct wave (zero
angle of incidence), there is no distinction between TM and TE polarizations, which is
obvious from symmetry. Figure 4-5 shows the average fraction of reflected and
transmitted power in a dB scale, for a case of a direct wave as a function of the dielectric
constant.
It is clear from Figure 4-5: Power Transmission/Reflection Coefficient for Direct Waves
that the smaller the dielectric constant, the more energy is transmitted and less is
reflected. For high dielectric constants, most of the energy is reflected and only a small
amount is transmitted. For a dielectric constant of around 34, (like wet ground, for
instance) half of the energy (3dB) is transmitted and half reflected. Figure 4-6: Reflection
Power Loss of a Direct Wave – Common Indoor Materials shows the reflection
coefficient in a dB scale for some common materials, in an indoor environment. It can be
seen, for example, that a gypsum board wall is not reflective at all, and around 10 dB are
lost on direct reflection, whereas a marble floor is a lot more reflective and only 5 dB of
loss occurs on direct reflection. Again, it must be noted that the examples in this figure
are rather general. For example, a glass with metal plating, a concrete wall with metal
reinforcement, or a wet wooden floor can be highly reflective and show a different
reflection coefficient.
© 2002, RFWaves Ltd.
Page 12 of 21
Radio Propagation
Rev. 1.0
Figure 4-5: Power Transmission/Reflection Coefficient for Direct Waves
Marble
Concrete
Glass
Gypsum board
Woo
Figure 4-6: Reflection Power Loss of a Direct Wave – Common Indoor Materials
This analysis assumes that the dielectric medium is a half infinite medium. It gives quite
good results for the reflection coefficient when the dielectric layer is fairly thick or when
the energy dissipation through the wall (caused by the imaginary part of the dielectric
constant) is high. Whenever it is required to estimate transmission or reflection
coefficients from / through thin layers, a more complicated approach has to be taken, as
© 2002, RFWaves Ltd.
Page 13 of 21
Radio Propagation
Rev. 1.0
will be explained in the next section. In such cases, we must consider the reflections from
the inner parts of the wall, which interfere with the main reflected wave. This causes
strong dependence of the reflection coefficient on the thickness of the wall. However,
when the wall is thick enough, and the attenuation factor (imaginary part of the dielectric
constant) is large enough, the attenuation dampens the inner reflections and the infinitely
thick layer analysis is a good estimation of reality when calculating the reflection
coefficient.
Summarizing this section, it is possible to estimate the propagation loss of a reflected
wave by knowing the dielectric qualities of the reflecting material and therefore the
reflection coefficient. It is also possible to know the amount of transmitted energy, which
can sometimes be used to place a minimum loss for propagation through finite thickness
layers, such as walls and floors. Transmission through dielectric layers will be discussed
in greater detail in the next section.
5 Effects of Walls and Floors
In an indoor environment, when several walls or floors separate the transmitter and
receiver, it is important to estimate the path loss through the walls / floors and include it
in the path loss calculation.
Theoretically, a wall or floor can be analyzed as one or more layers of dielectric material,
parallel to each other, each having a finite thickness and a complex dielectric constant
depending on the material from which the layer is made. When an electromagnetic wave
hits the wall, standing waves will be set up inside the wall. The wall can then be treated
as a transmission line with impedance mismatch junctions in the layer separation points,
including the 2 outer layers that interface with free air.
Applying Snell’s law (Equation 4.2) on each of the layers shows that the angle of
transmission from the wall into the air on its opposite side is equal to the angle of
incidence.
The reflection and transmission coefficients can then be calculated and the results are a
function of the angle of incidence, the dielectric properties of the wall and the
polarization of the incident wave. The calculation method will not be described here.
Figure 5-1 and Figure 5-2 present simulations of reflection and transmission coefficients,
respectively, at 2.44GHz for a 0.3m thick brick wall of dielectric constant 4-0.1i for both
TE and TM polarizations. It can be seen in Figure 5-1 and Figure 5-2, that for this
© 2002, RFWaves Ltd.
Page 14 of 21
Radio Propagation
Rev. 1.0
Figure 5-1: Reflection Coefficient of a Brick Wall, 2.44GHz, ε=4-0.1i
Figure 5-2: Transmission Coefficient of a Brick Wall, 2.44GHz, ε=4-0.1i
specific case, not more than 2 dB of power are lost in transmission through the wall at
both polarizations, when the angle of incidence is lower than 60 degrees. It can also be
seen that high losses appear in TM polarization when the angle is higher than 60 degrees.
Another interesting thing to point out is the perfect transmission that appears in TE
© 2002, RFWaves Ltd.
Page 15 of 21
Radio Propagation
Rev. 1.0
polarization at an angle of 65 degrees, where the wall appears almost invisible due to a
resonance phenomenon.
6 Antenna Height Affection – 2-Ray Model
When transmitting and receiving antennas are placed above a reflective surface, a
significant degradation of received signal is observed. This can be analytically described
by the ‘2-ray model’. This model treats the received power as an interference of 2 waves
– a direct wave and a reflected wave, as drawn in Figure 6-1. Basically, this is a simple
application of the dominant path approach explained in section 3, where the 2 dominant
paths of propagation are the direct wave and the one reflected from the ground.
Direct wave
Reflected
ε
Figure 6-1: 2-ray Model
The direct wave is treated as a free-space propagating wave and its propagation loss can
be calculated as described in section 2, whereas the reflected wave is treated using the
reflection coefficients described in section 4. The angle of incidence for the reflected
wave is related to the distance between the antennas and their heights above the reflecting
surface. The reflection coefficient, as we saw earlier, depends on the angle of incidence,
the dielectric properties of the surface, and the polarization of the incident wave.
The interference between the 2 waves must take into account the phase difference caused
by the difference in distance covered by both waves. An additional 180 degrees phase
shift must also be added to the reflected wave as its phase changes direction during
reflection.
Figure 6-2 and Figure 6-3 present simulation results of the propagation loss using the 2ray model, for a formica surface, with a dielectric constant of 4. This can be related to a
practical situation in which the antennas are placed on an office table, or above a polished
wooden floor. The propagation loss is described as a function of the distance between the
transmitter and the receiver. The simulated frequency is 2.4GHz. Figure 6-2 describes the
case where both antennas are at a height of 0.5 m and Figure 6-3 describes the case where
the antennas are at a 5 cm height.
The obtained path loss has minimum and maximum points. These are seen clearly in
Figure 6-3 and are a result of the phase shifts between the 2 paths that create zones of
© 2002, RFWaves Ltd.
Page 16 of 21
Radio Propagation
Rev. 1.0
constructive and destructive interference. In order to guarantee a communication link, it
is essential to make sure that the system’s dynamic range covers the deepest minima,
whenever it falls within the range of operation.
It can be proved mathematically, that at a certain distance, often called ‘the breakpoint
distance’, the last maxima occurs, and the received power starts degrading like 1/R4
instead of 1/R2 as in free space. This is caused when the distance covered by both
reflected and direct waves is almost equal, and the reflected wave goes through a
complete phase shift. In this situation, the reflection is almost total, and both waves show
destructive interference. The breakpoint distance is given by:
(6.1) Rbreakpo int =
4h1 h2
λ
Figure 6-2: 2-Ray Propagation Loss, 2.44GHz, ε=4, h1=h2=0.5m
© 2002, RFWaves Ltd.
Page 17 of 21
Radio Propagation
Rev. 1.0
Figure 6-3: 2-ray Propagation Loss, 2.44GHz, ε=4, h1=h2=5cm
For example, implementing Equation 6.1 in a frequency of 2.4GHz, when both antennas
are 0.5m above ground, the breakpoint distance is around 8m. At a height of 5cm, the
breakpoint distance is 8cm. Figure 6-3 shows that beyond the breakpoint distance, TM
polarization is better than TE polarization in terms of propagation loss.
Concluding this part, the 2-ray model predicts the appearance of dips and peaks before
we reach the breakpoint distance. Beyond it, we observe a high degradation of the signal.
Therefore, the closer the antennas are to the surface, the closer the breakpoint distance
and the higher the signal power decrease.
7 Summary
The complexity of wave propagation in a non-ideal environment has been presented, with
an attempt to show a practical approach to propagation loss estimation in such an
environment, which is very important in order to estimate a communication system’s
performance.
The ideal free-space propagation model was presented. An empirical model for predicting
propagation loss in an indoor environment was suggested, and compared to the free-space
model. It showed higher degradation of the signal with distance, and, as an averaging
approach, it also showed a relatively large prediction error. The concept of reflection and
transmission losses was presented via the calculation of transmission and reflection
coefficients of waves, which incident dielectric materials. It was shown that the reflection
and transmission coefficients are highly dependent on the dielectric properties of the
© 2002, RFWaves Ltd.
Page 18 of 21
Radio Propagation
Rev. 1.0
matter, the wave polarization and the angle of incidence. A simulation was presented to
demonstrate propagation loss and reflections from finite thickness layers, such as walls. It
was shown that the wall width and inner structure strongly influence the results. Finally, a
simulation of the ‘2-ray model’ was presented in order to show the effect of antenna
height on the propagation loss. It was shown that the reflected wave causes severe
degradation of the signal due to its interference with the directly propagating wave. The
2-ray model was shown as a demonstration of the ‘dominant path’ approach, which uses
the most dominant propagation paths in order to estimate propagation losses. The 2-ray
model showed a high degradation of the signal due to the interference with the wave
reflected from the ground.
The models presented in this article can be applied with relatively minimal effort, when
attempting to predict propagation loss in a complex environment, and give the RF system
designer a probable answer to the question of what is the maximum distance over which
the system in hand will work in a given environment.
References
H.L Bertoni , “Radio propagation for modern wireless systems”, Prentice Hall Inc,
2000
C.A Balanis, “Antenna theory – analysis and design”, 2nd edition J.W & Sons 1997,
Chapter 2 “Fundamental parameters of antennas”
J.D. Jackson, “Classical Electrodynamics”, 3rd edition, J.W & Ssons 1999 , Chapter
7 “Plane electromagnetic waves and wave propagation”
Hiroyuki Arai, “Measurement of mobile antenna systems”, Artech House Inc, 2001
© 2002, RFWaves Ltd.
Page 19 of 21
Radio Propagation
Rev. 1.0
© Copyright 2002, RFWaves Ltd. All rights reserved
Permission is given to review and use the material in this publication for personal reference
only and the said material cannot be copied, modified, used, distributed or reproduced in any
way without the prior written consent of RFWaves Ltd.
RFWaves Ltd. provides the information contained in this publication "as is" and without any
warranties. RFWaves Ltd. disclaims all express and implied warranties. In no event RFWaves
Ltd. shall be liable for any loss of profit and/or business, nor for any incidental or consequential
damages of any kind. RFWaves Ltd. may make changes to the material contained in this
publication at any time without notice and without obligation.
The Company’s products are covered by one or more of the following:
Taiwan Patent No. 155994, USA Patent No. 6,535,545.
Other patents pending.
For more information please contact:
RFWaves Ltd.
1c Yoni Netanyahu St.
Or-Yehuda 60376
Israel
Tel: +(972)-3-6344131
Fax: +(972)-3-6344130
E-mail: [email protected]
Website: www.rfwaves.com
© 2002, RFWaves Ltd.
Page 20 of 21
Radio Propagation
Rev. 1.0
1
Mr. Adi Shamir ([email protected]) graduated from the physics faculty of Tel Aviv University
and is working as a senior RF Engineer in RFWaves (www.rfwaves.com).
© 2002, RFWaves Ltd.
Page 21 of 21