Download Report

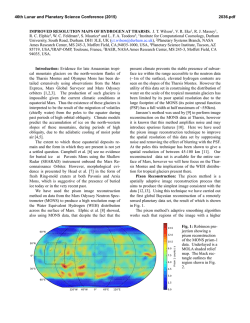
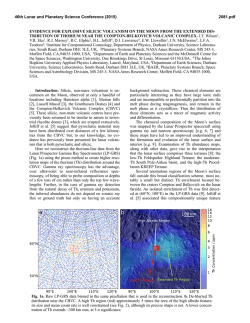
46th Lunar and Planetary Science Conference (2015)
2891.pdf
VOLCANIC SPREADING ON MARS: ROLE OF A BASAL DECOLLEMENT ON FAULTING AND
MAGMA PROPAGATION. N. Le Corvec and P. J. McGovern, Lunar and Planetary Institute, USRA, 3600 Bay
Area Blvd, Houston, TX, 77058.
Introduction: Mars possesses the largest volcanic
edifices in our solar system (e.g., Olympus Mons, Ascraeus Mons). These volcanoes have low slopes
(<10°), a caldera at their summit, and flank terraces
considered as low angle thrust faults. These structural
characteristics have been related to two main processes
[1, 2]: lithospheric flexure, and gravitational spreading.
The extent of flank terraces varies from one volcano to
another [3]. Such variation might represent differences
in the geometry of the edifice, the thickness of the lithosphere, and the coefficient of friction and thus the
amount of spreading.
The goal is to investigate the influence of lithospheric flexure and graviational spreading on the type
and extent of faulting evident at the surface of the volcano, and on the type of magmatic intrusion inside the
volcanic edifice.
Model: Axisymmetric finite element models using
COMSOL Multiphysics [4] of volcanic loading of an
elastic cone on top of an elastic lithosphere were created. For each model, a range of elastic lithosphere
thicknesses Te were studied (Table 1).
Finite Element Models
Models
Radius
(km)
1
100
Initial
Height
(km)
5
2
370
3
Slope
(°)
Te (km)
2.86
20 - 30 - 40
22
3.40
75 - 100 - 125
160
12
4.29
20 - 50 - 80
4
230
14
3.48
50 - 75 - 100
5
170
18
6.04
60 - 100 - 140
Table 1: Geometric setup of the different finite elements
models.
In each model, the radius of the lithosphere was set
to 2000 km to avoid boundary effects in the flexural
response. The volcano and the lithosphere have a density of 2800 kg/m3, and share the same elastic parameters: Poisson ratio  = 0.25 and Young’s Modulus E =
1011 Pa. In order to study volcanic spreading, we introduced a frictional contact between the volcanic edifice
and the lithosphere. The contact was characterized by
various friction coefficients (μ), from frictionless (μ =
0) to natural friction coefficients of basaltic rocks
(μ=0.6) [5]. The left boundary of the model represents
the symmetric axis, the upper boundary of the model is
set free, rollers are applied to the right boundary of the
model restricting horizontal displacement, and the bottom boundary is defined by an equilibrium balancing
the displacement of the lithosphere using “Winkler”
restoring forces [6] and counteracts the loading of the
pre-stressed layered lithosphere [7].
Preliminary Results: We tested 5 different models, described in Table 1. The type of faulting at the
surface of the volcano is mainly dependent on the ability of the volcano to spread (Fig. 1). In model 1, we
observe that volcanoes with a frictionless base display
circumferential thrust faults over most of their flanks.
The faulting at the base of the flank is dependent on the
thickness of the lithosphere (which controls the amplitude and wavelength of flexural response). Thin lithosphere will create radial normal faults at the base,
whereas thicker lithospheres produce strike-slip and
circumferential normal faults. Volcanoes with finite
friction bases show circumferential thrust extent limited to their summit, the flank is mostly cut by radial
thrust faults (Fig. 1) with their base cut by strike-slip
faults only for thin lithospheres.
Comparing our results with the minima elevation
found on several Martian volcanoes [3], we plotted the
vertical extent of circumferential thrusts against the
ratio between the volcano initial height and the lithosphere thickness (Fig. 2). We observe that the largest
vertical extent of circumferential thrusts along a volcano’s flank occur for the models with a frictionless base.
These elevation minima are comparable with the ones
found on Martian volcanoes (Fig. 2, shaded area) [3].
We observe that the vertical extent is however not a
systematic function of flexural response. Thinner lithospheres produce smaller elevation minima for model 5,
while it is the inverse for model 2. On the other hand,
models 1, 3 and 4 show elevation minima for their median lithospheric thickness.
Future Work: These results will be used to model
natural example on Mars. The locations of circumferential thrusts could yield information sufficient to constrain the elastic thickness under the volcanic edifice.
References: [1] Byrne P.K., et al. (2013) Geology, 41,
339-342. [2] McGovern P.J., et al. (2014) Geological
Society, London, Special Publications, 401. [3] Byrne P.K.,
et al. (2009) Earth and Planetary Science Letters, 281, 1-13.
[4] COMSOL Version 4.3b, 2013. [5] Schultz R.A. (1995)
Rock Mechanics and Rock Engineering, 28, 1-15. [6] Watts
A.B. (2001) Isostasy and Flexure of the Lithosphere, 458.
[7] Galgana G.A., et al. (2011) J. Geophys. Res., 116,
E03009.
46th Lunar and Planetary Science Conference (2015)
2891.pdf
Figure 1: Plots of the differential stress and the type of faulting on the volcano’s flank as a function of distance from the
volcano’s summit for model 1. Each curve represents a different coefficient of friction at the base of the volcano. The colors
represent the type of faulting: cyan corresponds to circumferential thrust (CT); orange to radial thrust (RT), yellow to strike slip
(SS), purple to radial normal (RN), and green to circumferential normal (CN).
Figure 2: Plot of the elevation minima of circumferential
thrust as a function of the ratio between the initial volcano
height and the lithospheric thickness. The shaded area
represents the range of elevation minima for Martian
volcanoes (e.g., Arsia Mons, Ascraeus Mons, Olympus
Mons) [3]. Inset: The surface of the lithosphere before
flexure represents the basal reference surface (0%), the
elevation of the volcano after deformation corresponds to
100%. Reworked from [3].