1. Educación

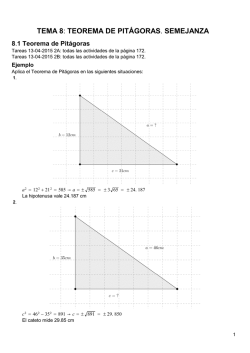
Plan de clase
Nombre: _______________________________________________________________ Grupo: ___ Núm.__
Curso: Matemáticas 9
Eje temático: F.E y M.
Contenido: 9.3.2. Aplicación de los criterios de congruencia y semejanza de triángulos en la resolución de problemas.
-------------------------------------------------------------------------------------------------------------------------------------------------------------
Intención didáctica 1. Que los alumnos usen los criterios de congruencia de triángulos, al resolver
problemas.
Organizados en equipos resuelvan los siguientes problemas.
1. Sea ABCD un cuadrilátero, ¿qué condiciones debe cumplir para que al trazar una de sus
diagonales resulten dos triángulos congruentes?
____________________________________________________________________________
______________________________________________________________
2. Se tienen dos triángulos con el mismo perímetro; los lados del LMN miden LM=5x+3,
LN=2x+2 y MN=8X-1; y los lados del RST miden RS=3x+13, RT=4x-8, y, ST=6x+9
a) ¿Los triángulos LMN y RST son congruentes? _________ ¿Por qué? _________
__________________________________________________________________________
__________________________________________________________________________
_____________________________________________________
3. Analicen los siguientes casos y determinen si se trata o no de triángulos semejantes,
argumenten sus respuestas:
a) Dos triángulos isósceles ABC y MNL en los que el ángulo desigual mide 45°.
b) Dos triángulos rectángulos cualesquiera.
4. El siguiente dibujo representa una parte lateral de una piscina, la cual tiene 2.3 m de ancho.
Con base en la información de la figura, contesten lo que se pide.
¿Qué profundidad (x) tiene la piscina?
¿Cuál es la distancia que hay desde el punto G hasta H?
1
Plan de clase
Nombre: _______________________________________________________________ Grupo: ___ Núm.__
Curso: Matemáticas 9
Eje temático: F.E y M.
Contenido: 9.3.2. Aplicación de los criterios de congruencia y semejanza de triángulos en la resolución de problemas.
-------------------------------------------------------------------------------------------------------------------------------------------------------------
5. Dos caminos que son paralelos entre sí, se unen por dos puentes, los cuales se cruzan por un
punto O, como se muestra en la figura.
Considerando las medidas que se muestran, ¿cuál es la longitud total de cada puente?
2