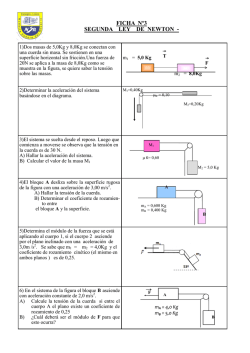
z A B D C y x
PRACTICA FÍSICA 1100 DINÁMICA Ing. Héctor Mitman P. ⃗⃗⃗2 = 4𝑖 + 11𝑗⃗ (𝑁) El objeto esta en 1. Un objeto de 4.00 kg está sujeto a dos fuerzas ⃗⃗⃗ 𝐹1 = 2𝑖 − 3𝑗⃗ (𝑁) 𝑦 𝐹 reposo en el instante t = 0. a) Calcular la aceleración del objeto, (b) ¿Cuál es su velocidad al cabo de 3.00 s? (c) donde está el objeto en ese instante? 2. Sobre una viga actúan tres fuerzas, dos de las cuales se ven en la figura junto con la resultante de las tres. ¿Cuál es la tercera fuerza? R =50 KN 20 KN 10KN 0.8 m 1.6 m 1.2 m 0.6 m 3. Sabiendo que la tención en AB es de 39.0 KN, determinar que valores deben tener las tensiones en AC y AD de forma que la resultante de las tres fuerzas aplicadas en A sea vertical. y A 48m C D 24 m O x 14 m 16 m z B 12 m 4. El bloque A pesa 15.0 N y el bloque B, 150 N. El coeficiente de rozamiento entre B y la superficie horizontal es 0.10. a) ¿Cuál es el peso del bloque C si la aceleración de B es 1.80 m/s 2 hacia la derecha? b) ¿Cuál es la tensión en cada cuerda? B A C 5. ¿A qué velocidad de rotación uniforme en rpm, alrededor del eje vertical AB, las esferas C y D de masas iguales m, comenzaran a levantar la Masa M en el mecanismo indicado en la figura. No se tendrán en cuenta los rozamientos ni los pesos de las cuatro barras articuladas de longitud L. La masa M puede deslizar libremente a lo largo del eje AB. Resolver para: m = 4.50 kg, M = 9.07 kg, L = 25.4 cm. A L L 30 30 C D L L M B 6. Un cuerpo de peso W descansa sobre el plano inclinado liso Una varilla unida al plano inclinado hace que el cuerpo gire con ella alrededor del eje vertical. Determine la rapidez en rpm para que la tensión e la cuerda sea igual al peso del cuerpo. 1.5 m 30O 7. Dos bloques A y B de masa 24.15 kg y 16.1 kg que tienen la posición indicada en la figura descansan sobre un marco que gira alrededor de un eje vertical con rapidez constante. El coeficiente de fricción entre los bloques y el marco es 0.20. Despreciando la masa y la fricción de la polea, ¿a cuántas rpm empezaran a deslizarse los bloques? ¿Cuál es la tensión en la cuerda en ese instante? 45cm 15cm B A 8. Un objeto de 4.00 kg está unido a una varilla vertical por medio de dos cuerdas, como se muestra en la figura. El objeto gira en un circulo horizontal a rapidez constante de 6.00 m/s. Encuentre las tensiones en las cuerdas. Rta. 108 N; 56.2 N M=3.00 kg R=10.0 cm 2.00 m 3.00 m 15.0 kg 3.00 m 2.00 m 10.0 kg P-8 9. P-9 Un cuerpo de 15.0 kg y uno de 10.0 kg están suspendidos, unidos por un cordón que pasa sobre una polea con radio de 10.0 cm y masa de 3.00 kg. El cordón tiene una masa despreciable y no se desliza sobre la polea. La polea rota sobre su eje sin fricción. Los cuerpos inician desde el reposo a 3.00 m de separación. Trate la polea como disco uniforme y determine la rapidez de los cuerpos cuando se pasan el uno al otro. 10. Una barra pesada AB se apoya por sus extremos contra dos planos inclinados perfectamente lisos de ángulos α y β respecto a la horizontal. Demostrar que la inclinación de la barra cuando esta en equilibrio viene dada por la expresión: 𝑎. 𝑐𝑡𝑔𝛼 − 𝑏. 𝑐𝑡𝑔𝛽 𝑡𝑔𝜃 = 𝑎+𝑏 B C b B a D θ A E Q Q α a β A P – 15 P-16 11. Una barra AC de longitud L, está articulada en A a una pared vertical con la cual forma el ángulo y esta sostenida, en su extremo superior C, por la cuerda horizontal BC. Una esfera lisa de peso Q y radio a, descansa entre la pared y la barra AC, hallar el valor del ángulo para el cual la tensión en la cuerda BC, sea mínimo. Determinar este valor para el caso que Q = 5000 N; L = 10 m y a = 2 m. 12. Determinar la fuerza P que iniciara el movimiento si el coeficiente de rozamiento para ambos bloques y el plano inclinado es 0.25. La polea carece de rozamiento. 10 kg 20 kg P 300 13. Para levantar un pesado bloque de piedra de 1000 kg, se emplea el dispositivo indicado en la figura. ¿Qué fuerza horizontal P será necesaria aplicar a la cuña a fin de alzar el bloque, si el coeficiente de rozamiento estático para todas las superficies en contacto es 0.25. No se tendrá en cuenta la masa de la cuña. W Q 1000 Kg A B P 15O 30o P – 18 P – 19 14. Dos bloques de caras planas, están unidos entre sí por una barra horizontal AB, en la forma indicada en la figura. El coeficiente de rozamiento es 0.30 sobre la pared vertical y 0.20 sobre el plano inclinado, el cual forma un ángulo de 30o con la horizontal. Hallar el valor mínimo de W compatible con las condiciones de equilibrio si Q = 3000 N. 15. A tiene una masa de 30.0 kg y radio 2.50 cm. B tiene un masa de 50.0 kg y radio 4.00 cm. Hallar Las Reacciones en las paredes. Se supone que A y B son cilindros circulares lisos. 3 4 A B A θ 100 N B x 13 cm P – 20 P - 21 16. En el sistema que se muestra en la figura, las poleas tienen fricción y peso despreciables. a) Determinar el peso de A para dar a B una aceleración hacia debajo de 0.6g. b) ¿Puede Usted encontrar el peso de A para dar a B una aceleración hacia arriba de 0.6g? 17. En el sistema de bloques conectados que se ve en la figura, el coeficiente de fricción cinética bajo los bloques A y C es 0.20. Calcule la aceleración de cada bloque y la tensión en el cable que los conecta. Las poleas se suponen sin fricción y de peso despreciable. 50.0 kg 20.0 kg A C 3 3 4 4 B 40.0 kg 18. El momento de inercia de la rueda mostrada en la figura es 8.0 kg.m2 . Tiene 40 cm de radio. Hállese la aceleración angular de la rueda producida por la masa de 10.0 kg, si la fuerza de fricción entre la masa y el plano inclinado es de 30 N. 5.0kg R=30 cm 10 kg 2.5kg 37 o P- 23 P - 24 19. La fuerza de fricción entre el bloque y la mesa en la figura es 20 N. Si el momento de inercia de la rueda es de 4.0 kg.m2, encuéntrese cuánto tardará el bloque en descender 60 cm después de que el sistema se ha soltado. 20. Una polea de 5.4 kg de masa con un radio de giro de 200 mm está unida como se muestra, a dos bloques. Despreciando el rozamiento en el eje, hallar su aceleración angular y la aceleración de cada bloque. 250 mm 100 mm 60 mm 150 mm 200 N 2.25 kg 4.5 kg P - 25 P- 26 21. Se enrolla una cuerda alrededor del tambor interior de una rueda y se tira de ella con una fuerza horizontal de 200 N. La masa de la rueda es de 50.0 kg y su radio de giro es 70.0 mm. Sabiendo que rueda sin deslizar, hallar la aceleración angular de la rueda. 22. La viga AB de la figura está articulada en A y sostenida en B por una cuerda vertical que pasa por una polea sin rozamiento en C y lleva en su extremo una carga P en la forma indicada. Determinar la distancia x, desde A, a la que debe colocarse sobre la viga una carga Q, para mantenerla en equilibrio en una posición horizontal. No se tendrá en cuenta el peso de la viga. C L A B X Q P 23. La polea doble de la figura tiene una masa de 13,60 kg y un radio de giro centroidal de 165 mm. Los bloques A y B están sujetos a cuerdas arrolladas en las poleas. El coeficiente de rozamiento entre el bloque B y la superficie es 0.25. Sabiendo que el sistema parte del reposo en la posición representada, hallar (a) la velocidad del bloque A al chocar con el suelo, (b) la distancia total que recorre el bloque B antes de detenerse. 9.10 kg 152 mm B 254 mm 11.35 kg A 900 mm 24. La barra uniforme OA de 100 N de peso, está articulada en O. Para sostenerla en la posición indicada se tiene el cable BD. Considerando que OB = ¾ OA, calcular la tensión en el cable y las reacciones en la articulación. A B C D P= 800 N 60o 30o A OA 25. Una barra prismática AB de peso Q y longitud L está sostenida por un pequeño rodillo en C y presiona contra una pared vertical lisa en A. Si se aplica una carga adicional P al extremo B de la barra, hallar la posición de equilibrio de ésta definida por el ángulo α que su eje forma con la horizontal. No se tendrá en cuenta el rozamiento en A y en C, así como tampoco el radio del rodillo en C. B P C α Q A a 26. Si el coeficiente de fricción cinética en todas las superficies es 0.25. Calcular la aceleración angular de la polea y las tensiones en las cuerdas. Que distancia recorren los cuerpos A y B en 2.00 s. El sistema parte del reposo. 600 mm 30.0 kg B 20.0 kg A 900 mm 3 4 27. La polea y el tambor de peso W p ruedan sin deslizar sobre un plano horizontal. La polea tiene un radio de giro con respecto a un eje horizontal que pasa por O de ko. Después que el peso W ha caído una distancia h a partir del reposo, ¿Cuál es la velocidad angular de W p? 28. Un cuerpo A desciende con una velocidad de 2.00 m/s cuando se aplica un torque constante en sentido contrario a las manecillas del reloj de 200 Nm a la polea cilíndrica que pesa 100 N y tiene un radio de giro de 40.0 cm. Hallar la máxima distancia a que caerá A después de haberse aplicado esa acción de freno. El cuerpo A pesa 300 N. R r 50 cm O P – 32 A P – 33 W 29. Localizar el centroide de la superficie que se muestra en la figura. y B b a C E y b P – 30 x A a D P – 31 30. De un cuadrado ABCD de lado a, debe recortarse un triangulo isósceles ADE. Hallar la altura y de este triangulo, de manera que su vértice E sea el centroide de la superficie sombreada restante. 31. Un bloque de masa m=20 kg, unido mediante una cuerda a una polea sin masa desliza a lo largo de una cuerda al centro de un carrete cilíndrico de masa M=5 kg, y radio R=0.1 m que rueda sin deslizar a lo largo de un plano inclinado 30º (véase la figura). a) Relacionar la aceleración del bloque y del centro de masas del cilindro. b) Calcular la aceleración del centro de masas del cilindro y las tensiones de las cuerdas. c) Calcular la velocidad del centro de masas del cilindro cuando ha descendido 3 m a lo largo del plano inclinado, partiendo del reposo. P – 36 P - 37 32. Determinar la fuerza constante P que le da al sistema de cuerpos una velocidad de 3.00 m/s después de haberse movido 4.50 m a partir del reposo. El coeficiente de rozamiento cinético para todas las superficies es 0.20. 25.0 kg 100 kg = 0.20 50.0 kg 33. Una esfera suspendida de un hilo se apoya en la pared como se indica. El centro C de la esfera se encuentra en la misma vertical que el punto de suspensión O. El hilo forma con la vertical el ángulo α y β es su angulo complementario. ¿Cuál es el coeficiente de rozamiento entre la esfera y la pared?. La masa de la esfera es m. O α 250 mm C β D A B A C R L 34. Se dobla el alambre homogéneo ABC como muestra la figura y se une en una articulación en C. Determinar la longitud L para la cual el tramo AB del alambre es horizontal. 35. En la figura el cabrestante se compone se compone de un mástil BE, una columna BD (vertical) y tres cables AD, CD, DE. Donde A, B, C están en el plano horizontal. Determinar las fuerzas en AD, CD, BD. D 20° 5m C 5m 45° 40° 40° 5m A B E 20.0 KN
© Copyright 2026