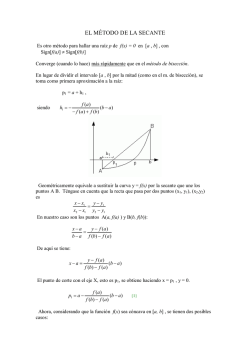
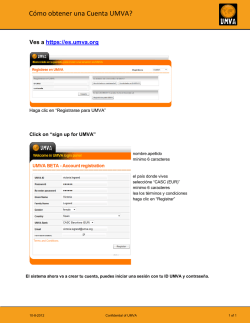
⎩ ⎨ ⎧ + = → = = 2 ba p bb a a ⎩ ⎨ ⎧ + = → = = 2 ba p b b p a 1.3 EL
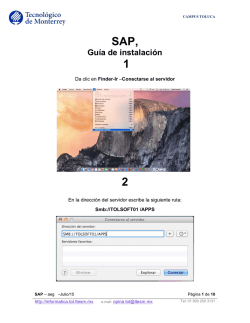
1.3 EL ALGORITMO DE BISECCIÓN (Método de Bolzano). Se trata de hallar los valores de x que cumplen f(x) = 0 Sea f definida en [a , b], t.q. f(a) y f(b) tengan signos opuestos, entonces por el corolario V.1 (llamado teorema de Bolzano), sabemos que existe un p [a , b] t.q. f(p)=0. El método consiste en ir tomando sucesivas aproximaciones p1 , p2 , ....., pn hacia el valor p. Tomando siempre el punto intermedio del intervalo. Inicialmente tomamos: a1 = a, b1 = b a1 a y a continuación b1 b p1 p1 a1 b1 tomamos el punto medio de (a1, b1): 2 a1 b1 b a a1 1 1 2 2 Este p = p1, sería la primera aproximación a la raíz. Si f(p1 )0 entonces f(p1 ) tendrá el mismo signo que f(a 1 ) o el mismo signo que f(b1 ). Si Sign[f(p1 )] = Sign[f(a1 )] entonces p [p 1 , b1 ], Entonces tomamos: a2 = p1, b 2 = b1 a2 p1 b2 b1 p2 a2 b2 2 6 Si Sign[f(p 1 )] = Sign[f(b1 )] entonces p [a 1 , p1 ], Entonces tomamos: a2 = a1, b2 = p1 Etc. hasta encontrar un f(p) = 0, o bien el intervalo [a n , b n ] es inferior a una tolerancia TOL prefijada. ALGORITMO: Para hallar una solución de f(x) = 0 , dada la función f en el intervalo [a, b] donde f(a) y f(b) tienen signos opuestos. Entradas: extremos a y b; tolerancia TOL; cantidad máxima de iteraciones N Salida: solución aproximada p, o mensaje de fracaso. Paso 1: Tomar i = 1; Paso 2: Mientras que i N seguir los pasos 3-6; Paso 3: Tomar p = a + ½ (b-a) ; % Calcular p i . Paso 4: Si f(p) = 0 ó ½ (b-a) < TOL entonces Salida p , PARAR. Paso 5: Tomar i = i + 1; Paso 6: Si f(a) . f(p) > 0 entonces tomar a = p, de lo contrario, tomar b = p; Paso 7: Salida (‘El método fracasó después de N intentos’); PARAR. 7
© Copyright 2026