1. No category

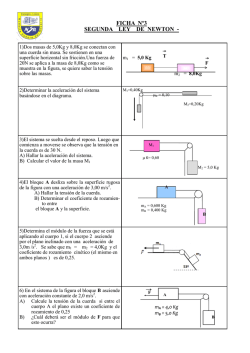
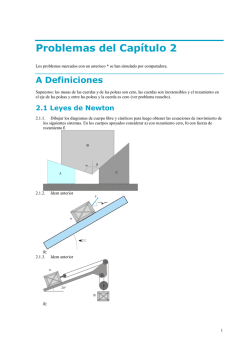
Ejercicios de MCU 5º Biológico y Científico FISICA
San Felipe 2014
1) Una bola de pequeñas dimensiones y masa m=5 kg se sujeta a una
cuerda de longitud L=2m para hacerla girar describiendo una
Circunferencia horizontal a una velocidad de módulo constante v0.
Sabiendo que la cuerda forma un ángulo α = 40º con la vertical,
determinar la tensión de la cuerda y el módulo de la velocidad v0 de la
bola.
2) Un cuerpo describe un M.C.U y da una vuelta completa en 6,3 s,
en el sentido indicado si el radio vale 30cm. Determinar
a) Los vectores velocidad en los puntos A y B .
b) El vector aceleración media entre A y B.
Represéntelo
3) Las poleas A y B están ligadas por una correa. Sus radios son
RA=20 cm, RB= 10cm . La polea A gira a 120 R.P.M.:
a) Determinar la frecuencia de giro de la polea B.
b) Determinar la aceleración centrípeta de un punto de
la correa cuando rodea a B.
A
 = 60º
B
RB
RA
4) Cual es la velocidad angular, en rad/s, de una rueda que gira a 300 r.p.m.?
Si el diámetro de la rueda es de 90 cm calcular la velocidad instantánea en un punto de su periferia
5) Un satélite describe un movimiento circular uniforme alrededor de la Tierra. Si su velocidad angular es de
0,5 vueltas por hora, calcula el número de vueltas que da en un día.
6) Dos bloques de masas m1=2 kg y m2=3 kg unidos por una cuerda
inextensible giran con la misma velocidad angular ω, describiendo dos
trayectorias circulares situadas en el plano horizontal de radios r1=30 cm
y r2=50 cm, respectivamente. Sabiendo que la tensión de la cuerda que
une el centro de las trayectorias con el bloque de masa m1 es de 40 N.
Calcular:
a) La tensión de la cuerda que une ambas masas.
b) La velocidad angular de giro ω
7) Un juego de un parque de atracciones consta de una
plataforma circular de 8 m de diámetro que gira. De la plataforma
cuelgan “sillas voladoras” suspendidas de unas cadenas de 2.5 m
de longitud. Cuando la plataforma gira las cadenas que sostienen
los asientos forman un ángulo de 28º con la vertical.

¿Cuál es la velocidad angular ω de rotación?

Si la masa del asiento y del niño es de 50 kg. ¿Cuál es la
tensión de la cadena?.
8) Una masa m que está sobre una mesa sin rozamiento está unida
a una masa M colgada mediante una cuerda que pasa por un
agujero practicado en la mesa. El cuerpo de masa M está en reposo
mientras que el cuerpo de masa m describe un movimiento circular
uniforme de radio r.
a) Haz un esquema de las fuerzas que actúan sobre cada cuerpo.
b) Calcula la velocidad v con el que se mueve el cuerpo de masa m.
c) Indica cuál es la aceleración del cuerpo de masa m.
Datos: m = 1 kg, M = 4 kg, r = 0,1 m
(Solución: 2 m/s 0 m/s2 y 40 m/s2
9) Una cabina cilíndrica gira respecto a su eje con una velocidad de 5 rad/s.
En contacto con la pared interior hay un cuerpo que gira solidariamente con
la cabina.
El coeficiente de rozamiento entre la pared y el cuerpo es 0,2. Cuál es el radio
de la cabina?
Solución: 1,96 m
10) Un coche toma una curva sin peralte que tiene un radio de 30 m. Si el coeficiente de rozamiento entre
los neumáticos y el asfalto es 0,6, ¿cuál es la velocidad máxima a la que puede tomar la curva sin que
derrape?
11) Una curva de 30 m de radio de giro tiene un ángulo de peralte de 22º. Determine el valor de la velocidad
máxima a la que una moto puede tomar esa curva si suponemos que está mojada y no hay rozamiento.
Solución v = 10,5 m/s
12) Cuando un auto toma una curva en una ruta horizontal, la fuerza neta que lo
hace girar se origina en el rozamiento estático entre las ruedas y el piso. Para estos
no patinen en las curvas, las rutas son peraltadas, (inclinadas hacia el centro de
giro). De este modo la fuerza normal tiene una componente vertical, que anula al
peso y otra horizontal, centrípeta. Observa el diagrama de fuerzas de la siguiente
figura e indica:
a) ¿Quienes ejercen las fuerzas nombradas R y W sobre el auto?
b) Escribe una ecuación para la aceleración centrípeta en función de la fuerza
reacción normal y el ángulo de peralte.