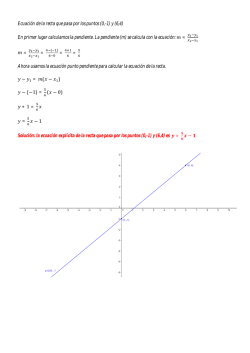
Soluciones de la Hoja 1
Matemática Discreta HOJA 1 RESUELTA 1) i) Demostrar que una recta y una circunferencia del plano real se intersecan en, como máximo, dos puntos. ii) Usando el apartado i) demostrar que por tres puntos alineados no pasa ninguna circunferencia. i) Sea una circunferencia C de ecuación: (x − c1 )2 + (y − c2 )2 = r2 , donde (c1 , c2 ) es su centro y r su radio. Sea una recta R de ecuación: y = mx + n si es no vertical y x=a si es vertical. Para buscar la intersección R ∩ C hay que resolver el sistema formado por la ecuación de R y la de C . En el caso en que la recta es vertical, necesariamente x = a por lo que al sustituir en la ecuación de C tenemos la ecuación: (a − c1 )2 + (y − c2 )2 = r2 , que es una ecuación en la incógnita y de grado dos y por lo tanto con, como máximo, dos soluciones y0 , y1 . Por tanto C ∩ R contiene en este caso, como máximo, dos puntos (a, y0 ) y (a, y1 ). En el caso en que la recta es no vertical, necesariamente y = mx + n por lo que al sustituir en la ecuación de C tenemos la ecuación: (x − c1 )2 + (mx + n − c2 )2 = r2 , que es una ecuación en la incógnita x de grado dos y por lo tanto con, como máximo, dos soluciones x0 , x1 . Por tanto también en este caso la intersección C ∩ R contiene como máximo, dos puntos (x0 , mx0 + n) y (x1 , mx1 + n). ii) Supongamos que existiera una circunferencia C que pasa por tres puntos alineados p, q y r. Entonces la intersección de C y la única recta que pasa por p, q y r contiene tres puntos, contradiciendo el apartado i). 2) Demostrar la siguiente propiedad del valor absoluto, conocida como desigualdad triangular. Sean x, y números reales entonces: |x + y| ≤ |x| + |y|. 1 2 Razonamos por casos: Caso 1) x, y ≥ 0. Entonces |x + y| = x + y , |x| = x e |y| = y con lo que se tiene la desigualdad del enunciado (de hecho una igualdad). Caso 2) x, y ≤ 0. Entonces |x + y| = −x − y ,|x| = −x e |y| = −y con lo que se tiene la desigualdad del enunciado (de hecho una igualdad). Caso 3) x ≥ 0, y ≤ 0 (aquí queda englobado el caso y ≥ 0, x ≤ 0 que es completamente similar, cambiando los nombres de las variables). Este caso se descompone en dos: 3.1 x ≥ −y . Entonces |x + y| = x + y , |x| = x e |y| = −y de modo que la desigualdad del enunciado se puede escribir como: x + y ≤ x − y. Que es equivalente a y ≤ 0 y por tanto cierta. 3.2 x ≤ −y . Entonces |x + y| = −x − y , |x| = x e |y| = −y de modo que la desigualdad del enunciado se puede escribir como: −x − y ≤ x − y. Que es equivalente a x ≥ 0 y por tanto cierta. 3) Sea el entero xn denido recursivamente como: x1 = 2, xn = xn−1 + 2n (n ≥ 2). Demostrar por inducción que para cada n natural: xn = n(n + 1). Base de inducción: x1 = 2 = 1(1 + 1) y por tanto la tesis es cierta para n = 1. Paso de inducción: usamos la fo¯mula recursiva para obtener: xn+1 = xn + 2(n + 1). Ahora por la hipótesis de inducción: xn+1 = n(n + 1) + 2(n + 1). Y por tanto: xn+1 = (n + 1)(n + 2). Como queríamos demostrar. 4) i) Demostrar que la siguiente expresión de lógica de predicados es siempre verdadera: ∃x (P (x) ∧ Q(x)) ⇒ (∃x P (x) ∧ ∃x Q(x)). ii) Demostrar que la sentencia recíproca no es siempre verdadera. i) Si la hipótesis es falsa la sentencia es verdadera. Si la hipótesis es verdadera entonces hay una constante a en algún universo de discurso de modo que P (a) ∧ Q(a) es verdadera. Entonces P (a) es verdadera por lo que ∃x P (x) es verdadera. De igual manera Q(a) es verdadera por lo que ∃x Q(x) 3 es verdadera. Hemos comprobado que si la hipótesis es verdadera también lo es la tesis, por tanto la implicación es verdadera. ii) Si la sentencia recíproca es verdadera entonces en particular es verdadera si tomamos Q(x) := ¬P (x). Para este valor de la función proposicional Q(x) se tiene que ∃x(P (x) ∧ Q(x)) es F . Por tanto, en este caso particular, la conclusión de la sentencia recíproca es F . Pero la hipótesis puede ser verdadera, lo que hace que la implicación no sea siempre V : tomando por ejemplo P (x) :=x es par, se tiene que ∃xP (x) es V y que ∃x¬P (x) es también V . 5) Sea el conjunto U de las personas. Sean los predicados P (x) :=x habita en el primer mundo, Q(x) :=x tiene una renta mensual superior a 500 dólares, R(x) :=x está sin alfabetizar. i) Escribir en lenguaje formal los siguientes predicados. Para cada persona se verica que si habita en el primer mundo entonces su renta mensual es superior a 500 dólares ∀x ∈ U (P (x) ⇒ Q(x)) hay personas en el primer mundo cuya renta es superior a 500 dólares y sin alfabetizar ∃x ∈ U (P (x) ∧ Q(x) ∧ R(x)) toda persona del primer mundo está alfabetizada ∀x ∈ U (P (x) ⇒ ¬R(X)) ii) Escribir su negación en lenguaje formal y natural. La sentencia ¬(∀x ∈ U (P (x) ⇒ Q(x))) es equivalente a: ∃x ∈ U (P (x) ∧ ¬Q(x)) lo que en lenguaje natural es existen personas del primer mundo cuya renta es inferior o igual a 500 dólares. La sentencia ¬(∃x ∈ U (P (x) ∧ Q(x) ∧ R(x))) es equivalente a: ∀x ∈ U ¬(P (x) ∧ Q(x)) ∨ ¬R(x) o equivalentemente: ∀x ∈ U (P (x) ∧ Q(x)) ⇒ ¬R(x) lo que en lenguaje natural es cada persona del primer mundo con renta superior a 500 dolares está alfabetizada. La sentencia ¬(∀x ∈ U (P (x) ⇒ ¬R(x))) es equivalente a: ∃x ∈ U (P (x) ∧ R(x)) lo que en lenguaje natural es hay personas del primer mundo no alfabetizadas. 4 6) Formalizar el siguiente razonamiento. Identicar las premisas y la conclusión. Vericar si es correcto: Si lo intento con ahínco y tengo talento, me convertiré en músico si me convierto en músico, seré feliz Si no voy a ser feliz, entonces no lo intento con ahínco o no tengo talento Sea i :=intentar con ahínco, t :=tener talento, m :=ser músico, f :=ser feliz. La hipótesis primera es H1 := (i ∧ t) ⇒ m La hipótesis segunda es H2 := m ⇒ f La conclusión es: T := ¬f ⇒ (¬i ∨ ¬t) El razonamiento es por tanto: H1 H2 T y será valido si A := (H1 ∧ H2 ) ⇒ T es una tautología. La proposición A no será una tautología si T es falso y (H1 ∧ H2 ) verdadero. Si T es falso es porque ¬f es verdadero y ¬i ∨ ¬t es falso. Esto quiere decir: f := F, i := V, t := V. Como i := V y t := V entonces para que H1 sea verdadero debe tenerse: m := V. Como m := V entonces para que H2 sea verdadero, f tiene que ser verdadero lo que da una contradicción, entonces A es una tautología y el razonamiento es por tanto válido. Esto concluye el ejercicio. Obsérvese que T es equivalente a su contrarrecíproca: (i ∧ t) ⇒ f. Y que por tanto estamos hablando de la tautología que justica el método de demostración directa.
© Copyright 2026