1. No category

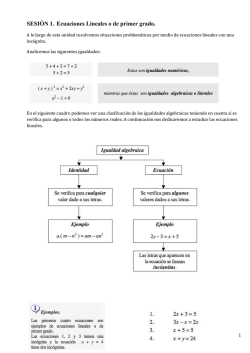
ECUACIÓN LINEAL CON UNA INCÓGNITA
OBJETIVOS:

Resolver ecuaciones lineales con una variable.

Utilizar la solución de ecuaciones lineales para resolver problemas de aplicación.
INTRODUCCIÓN:
Como hemos visto, una ecuación es una igualdad que contiene una o más cantidades
desconocidas llamadas incógnitas. Las ecuaciones se han estudiando desde hace mucho
tiempo y existen diferentes tipos de acuerdo a las expresiones que la conforman. En este
taller se proponen solucionar ecuaciones algebraicas con una incógnita y además resaltar su
importancia en la solución de problemas relativos a la Economía.
DESARROLLO:
Una ecuación lineal de una variable tiene la forma corriente de: ax + b = 0, donde a y b son
números reales y a  0. Se llama lineal porque el exponente de x es uno. La presencia de
términos que tengan exponentes diferentes de uno (x2, x3, x-1) en una ecuación, la excluye
de aquellas consideradas lineales o de primer grado.
Para resolver una ecuación de primer grado con una incógnita se transponen, si es
necesario, todos los términos que contienen la incógnita a un miembro de la ecuación y
todos los términos conocidos al otro miembro de la ecuación, para finalmente despejar la
incógnita.
Ejemplo:
Hallar la solución de cada una de las siguientes ecuaciones lineales:
a) 3x + 4 = 5(x – 2)
Solución: Se quitan los paréntesis, se transponen y reducen términos semejantes y se
despeja la variable.
3x + 4 = 5(x – 2)
– 2x = – 14
→
3x + 4 = 5x – 10
x = – 14/– 2
→
3x – 5x = – 10 – 4
x=7
b) 5x – (3x – 7) – [4 – 2x – (6x – 3)] = 10
Solución: Se destruyen paréntesis y corchetes, se transponen y reducen términos
semejantes; y por último, se despeja la incógnita.
5x – (3x – 7) – [4 – 2x – (6x – 3)] = 10
5x – 3x + 2x + 6x = 10 – 7 + 4 + 3
↓
5x – 3x + 7 – [4 – 2x – 6x + 3] = 10
2x + 8x = 3 + 7
↓
5x – 3x + 7 – 4 + 2x + 6x – 3 = 10
10x = 10
x=1
c)
4
10
1
 2

2u  3 4u  9 2u  3
Solución: Se factorizan los denominadores y se multiplica cada fracción por el mínimo
común múltiplo de los denominadores dados, para así poder eliminar los denominadores.
4
10
1
 2

2u  3 4u  9 2u  3
→
4
10
1


2u  3 (2u  3)(2u  3) 2u  3
4
10
1
 (2u  3)(2u  3) 
 (2u  3)(2u  3) 
 (2u  3)(2u  3)
2u  3
(2u  3)(2u  3)
2u  3
4(2u + 3) + 10 = 1(2u – 3)
8u + 22 = 2u – 3
6u = – 25
d)
→
8u + 12 + 10 = 2u – 3
8u – 2u = – 3 – 22
u=–
25
6
4
10
1
 2

2u  3 4u  9 2u  3
Solución:
Otra forma de resolver este ejercicio es hallando el m.c.m. de los
denominadores y resolver la suma de fracciones dadas; por último, resolver la igualdad
de fraccionarios que resulta.
4
10
1
 2

2u  3 4u  9 2u  3
4(2u  3)  10
1

(2u  3)(2u  3) 2u  3
8u + 22 = 2u – 3
4
10
1


2u  3 (2u  3)(2u  3) 2u  3
→
→
8u  12  10 1

(2u  3)
1
8u – 2u = – 3 – 22
6u = – 25
u=–
25
6
Ejemplo:
1. Un hombre desea invertir una parte de sus 200.000 pesos en una cuenta de ahorro que
produce 6% de interés simple y el resto en un fondo de inversión que produce el 10%
de interés simple. ¿Qué cantidad debe invertir en cada uno de ellos para obtener una
ganancia del 8% después de un año?
Solución: Lo primero que se debe hacer es determinar la cantidad desconocida, la cual se
consigue analizando la pregunta del problema. En este caso, no se sabe que cantidad de
dinero se invirtió al 6% de interés, por lo tanto, la llamaremos x; el resto, 200.000 – x se
invertirá al 10% y 0.1 (200.000) será la ganancia obtenida. Por consiguiente, se obtiene
la siguiente ecuación:
0.06x + 0.1 (200.000 – x) = 0.08 (200.000)
Resolvamos la ecuación:
0.06x + 20.000 – 0.1x = 16.000
0.06x – 0.1x = 16000 – 20.000
Agrupando términos semejantes
– 0.04x = –4.000
Reduciendo términos semejantes.
Despejando la variable:
x=
 4000
 0.04
x = 100.000
En consecuencia, deben depositarse 100.000 pesos en la cuenta de ahorros y
200.000 – 100.000 = 100.000 dólares en el fondo de inversión.
Ejemplo:
2. Una fábrica de camisas paga $ 140.000 de arriendo por el local donde confecciona y
vende sus camisas. El costo del material es la mitad de la mano de obra. ¿Cuánto
pagará por mano de obra y cuánto por material para que los costos totales sean de $
500.000?
Solución: Según la pregunta del problema hay dos cantidades desconocidas; como se debe
obtener una ecuación lineal con una variable, debemos establecer una relación entre ellas.
Esa relación la conseguimos en la frase anterior a la de la pregunta. Si hacemos que x
x
denote el costo de la mano de obra, entonces,
será el costo del material. Como se sabe
2
que:
Costo total = Costo fijo + Costo variable
Obtenemos la siguiente ecuación:
x+
Resolviéndola:
3
x = 360000
2
x+
x
+ 140000 = 500000
2
x
= 500000 – 140000
2
x = 360000.
2
3
x = 240000
Entonces, paga $240000 por la mano de obra y $120000 por los materiales