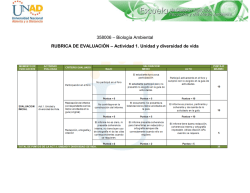
biología
Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria PROPUESTA HIDALGO 1 er grado Ma. Guadalupe Flores Barrera Andrés Rivera Díaz BIOLOGÍA Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria, Propuesta Hidalgo (ECAMM-Hidalgo), ha sido desarrollado e implementado por la Coordinación Estatal del Programa EMAyCIT-Hidalgo, con el apoyo de la Subsecretaría de Educación Básica de la Secretaría de Educación Pública del Estado de Hidalgo y, sobre todo, del Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, particularmente del Departamento de Matemática Educativa, del cual surge la Propuesta Nacional. Autores de ECAMM-Hidalgo Ma. Guadalupe Flores Barrera Andrés Rivera Díaz [email protected] [email protected] Este material ha sido implementado en las escuelas secundarias del Estado de Hidalgo, en sus tres modalidades: Generales, Técnicas y Telesecundarias con apoyo de las Direcciones, Supervisiones y Jefaturas de Sector, pero sobre todo por los Coordinadores de Zona Escolar ECAMM-Hidalgo. Coordinadores Zona Escolar ECAMM-Hidalgo Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria, Propuesta Hidalgo 1er. grado BIOLOGÍA Revisión: Ramón Guerrero Leyva Formación y diseño: Ana Garza © ECAMM Hidalgo 2010 © Ángeles Editores, S.A. de C.V. 2011 Campanario 26 San Pedro Mártir, Tlalpan México, D.F. 14650 e-mail [email protected] www.angeleseditores.com Primera edición: agosto de 2011 Segunda edición: agosto de 2012 ISBN 978-607-9151-07-2 Miembro de la Cámara Nacional de la Industria Editorial Reg. Núm. 2608 Impreso en México Acosta Ramírez Merit Aguilar Castelán Isidoro Anaya Velázquez Max Julio Andrade Castillo Dimas Alexandro Avilés Hernández Jaime Bahena Mejía Mireya Bautista de la Cruz Natalio Calva Martínez Fortino Alberto Castro Ramírez Dimna Berenice Clemente López Antonio Cuevas Covarrubias Maribel Daniel García Nancy Escobedo Garrido Martha Elva Esteban Reyes Edgar Estrada Tolentino Nancy Félix Lara Filiberto Flores Morita Néstor Gálvez Marín Marlén García Soto Federico Gómez Martínez Miguel González Medina Alejandro Alberto Guerrero Romero José Manuel Gutiérrez González Fernando Hernández Blancas Patricia Dayanara Hernández Cortés Victorino Hernández Hernández Aricela Hernández Juárez Áureo Hernández Mendoza Camerino López Lugo Eliseo Manzano Salinas Elias Martínez Martínez Isidro Medina Abrego Gildardo Miranda Fernández Israel Miranda Sánchez Ma. Eleazar Monroy Villanueva Yareth Montoya Gress Luis Morales Gómez Martín Paredes Ortega Jorge Antonio Perales Salvador Cuauhtémoc Pérez Reyes Jesús Ramírez Castillo Hilda Ramírez García Martha Esperanza Ramírez Rico Martha Catalina Rojas Ángeles Crisóforo Rojas Reyna Tomás Romero Camargo Jeimy Rubio Rubio Ma. Virginia Salazar Lara Gastón Sánchez Castillo Gracia Patricia Sánchez Díaz Antonio Saúz Torres Araceli Tena Rodríguez Jesús Tolentino Ruíz Rebeca Vázquez Terán Nora Alejandra Velázquez Serrano Diego Vidal Fernández Leticia Ruby Villegas Villegas Gamaliel Zermeño Peralta Jorge Alonso Contenido Introducción.............................................................................................. 5 Cómo está organizado este libro............................................................... 7 Programación Biología Primer Grado........................................................ 9 Septiembre La importancia de las Gráficas (I)............................................................ 12 La importancia de las Gráficas (II)........................................................... 16 Eras geológicas........................................................................................ 20 Técnicas de fechamiento de fósiles (I)..................................................... 24 Octubre Técnicas de fechamiento de fósiles (II).................................................... 25 ¿Cuántas especies existen?..................................................................... 27 Crecimiento exponencial de células (I).................................................... 31 Crecimiento exponencial de células (II)................................................... 34 Noviembre Dieta y actividad corporal (I)................................................................... 36 Dieta y actividad corporal (II).................................................................. 40 Nutrición (I)............................................................................................. 43 Nutrición (II)............................................................................................ 47 Diciembre y Enero Nutrición (III)........................................................................................... 51 Bajar de peso = Alimento + ejercicio....................................................... 53 La respiración como fenómeno cíclico (I)................................................ 56 La respiración como fenómeno cíclico (II)............................................... 58 Datos sobre enfermedades respiratorias (I)............................................ 60 Datos sobre enfermedades respiratorias (II)........................................... 61 ECAMM-Hidalgo Febrero Escalas entre animales de diferentes tamaños (I)................................... 62 Escalas entre animales de diferentes tamaños (II).................................. 64 Datos sobre las drogas y el ritmo cardiaco (I).......................................... 68 Datos sobre las drogas y el ritmo cardiaco (II)......................................... 69 Marzo y abril Los experimentos de Mendel (I).............................................................. 71 Los experimentos de Mendel (lI)............................................................. 77 Distribución genética (I).......................................................................... 78 Distribución genética (II)......................................................................... 82 ADN (ácido desoxirribonucleico)............................................................. 84 ARN (ácido ribonucleico)......................................................................... 86 Mayo Distribución de edades en poblaciones................................................... 88 Epidemias................................................................................................ 92 Competencia entre dos especies............................................................. 97 Interacción depredador-presa............................................................... 101 Junio Fibonacci y sus conejos (I)..................................................................... 103 Temperatura corporal............................................................................ 105 Tipos sanguíneos (I)............................................................................... 107 Tipos sanguíneos (II).............................................................................. 111 Introducción Las Herramientas Computacionales (HC) suponen un revolucionario avance en nuestra sociedad. Presenciamos una era de cambio y de modificaciones constantes que influyen significativamente en nuestras vidas. Mantenernos expectantes o tomar las riendas de los procesos de cambio que nos pueden ayudar a construir un mundo sin barreras, un mundo mejor, es una elección a realizar de forma particular por cada uno de nosotros. En el ámbito educativo las HC constituyen una importantísima ayuda para favorecer los aprendizajes escolares, particularmente de las matemáticas y de las ciencias, pues son un reforzador didáctico, un medio para la enseñanza individualizada y una herramienta fundamental de trabajo para el profesor. En definitiva pudiéramos preguntarnos: ¿Qué aspectos caracterizan a las HC que las hacen tan especiales en la educación? Una reflexión alrededor de esta pregunta nos conduce a definir un grupo de aspectos que las podrían caracterizar: 1. Fomentan el aprendizaje continuo por parte del profesor, pues éste tendrá que estar actualizado para planificar con éxito las actividades que realizarán los estudiantes. 2. Las HC no sólo pueden ser objeto de estudio sino que deben ser herramientas indispensables para el alumno, tienen que ser integradas al entorno educativo. 3. Garantizan el desarrollo de una enseñanza significativa y forman parte de una educación integral. 4. Dinamizan el papel del profesor y del alumno. Este último, de sujeto pasivo dentro del proceso didáctico, pasa a ser protagonista del mismo junto al profesor, el cual tendrá como función rectora la orientación en el uso de las herramientas tecnológicas que sean utilizadas en el proceso. 5. Humanizan el trabajo de los profesores, pues ellos desarrollarán sus actividades con el apoyo de las tecnologías, economizando tiempo y energía. Propuesta Hidalgo 1er Grado BIOLOGÍA 5 Además de estas ventajas que nos proporcionan las Herramientas Computacionales en el proceso de enseñanza, es bueno destacar que también permiten lograr una mejor interdisciplinariedad, es decir, se puede relacionar el contenido con el de otras asignaturas contribuyendo así a una formación más eficiente y de carácter integral de nuestros estudiantes, particularmente el de las ciencias. Por lo anterior, la Secretaría de Educación Pública del Estado de Hidalgo ha implementado el Programa Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria, Propuesta Hidalgo (ECAMMHidalgo) a través de la Coordinación Estatal de los profesores Ma. Guadalupe Flores Barrera y Andrés Rivera Díaz. Para dar continuidad al programa, dichos profesores imparten un curso-taller programado, un día al mes durante el ciclo escolar, al equipo de Coordinadores de las Zonas Escolares del Estado, para que a su vez ellos lo multipliquen, también un día al mes, con los profesores que imparten ciencias en sus zonas correspondientes. Las reuniones mensuales son un espacio de formación y actualización docente para el intercambio de experiencias, metodologías y conocimientos sobre la Hoja electrónica de cálculo, herramienta tecnológica que forma parte de la propuesta original elaborada por la Subsecretaría de Educación Básica de la Secretaría de Educación Pública (SEP), en colaboración con el Instituto Latinoamericano de la Comunicación Educativa (ILCE). Como producto de ello se han diseñado y compilado los textos ECAMM-Hidalgo, para cada grado escolar de educación secundaria. Por último, sabedores de que contamos con una comunidad educativa comprometida, utilizaremos el presente material para beneficio de nuestros alumnos. Profr. Joel Guerrero Juárez Secretario de Educación Pública SEPH 6 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Cómo está organizado este libro PRESENTACIÓN El libro Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria, Propuesta Hidalgo, Biología, es una compilación y diseño de actividades didácticas que contempla el uso de hojas electrónicas de cálculo. El texto cumple, en forma paralela, con los planes y programas de estudio vigentes para las modalidades de Educación Secundaria (General, Técnica y Telesecundaria). En la mayoría de las actividades seleccionadas, la construcción y el uso de hojas electrónicas de cálculo cuentan con un sustento teórico y/o empírico, respectivamente, que respaldan su valor como herramienta mediadora del aprendizaje en lo cognitivo y en lo epistemológico. La propuesta Hidalgo es trabajar una sesión a la semana en el aula de medios o espacio asignado con equipos de cómputo, complementando las sesiones previas en el salón de clase. Esto implica que desde el inicio del curso escolar, los directivos deben asignar en los horarios, de forma explícita, la sesión ECAMM-Hidalgo a cada grupo. En el espacio para desarrollar el Programa ECAMM-Hidalgo, el profesor guía a los estudiantes en su trabajo con el ambiente computacional y con las hojas de actividades didácticas programadas semanalmente en el libro. Con las actividades se pretende que los alumnos alcancen cada vez mayores niveles de modelación matemática, para ello la programación de las actividades es como en el siguiente ejemplo: Semana 1 2 Bloque II. La nutrición Importancia de la nutrición en la obtención de energía y en la conservación de la salud. Diversas formas de nutrición de los seres vivos y su relación con la adaptación. NOVIEMBRE Herramienta Dieta y actividad corporal (I) Dieta y actividad corporal (II) Página 36 40 Propuesta Hidalgo 1er Grado BIOLOGÍA 7 En general, en el espacio ECAMM-Hidalgo el profesor debe motivar a los alumnos a: • Explorar • Formular y validar hipótesis • Expresar y debatir ideas • Aprender comenzando con el análisis de sus propios errores Las sesiones ECAMM-Hidalgo se organizan a partir de actividades didácticas en las cuales los alumnos reflexionan sobre lo que han realizado con la computadora, y lo sintetizan para comunicarlo; por otro lado, estas actividades ya contestadas proporcionan información al profesor acerca de la comprensión que los alumnos tienen de los conceptos involucrados en las ciencias: Biología, Física y Química. Finalmente, una reflexión: La educación es la base del progreso en cualquier parte del mundo y en la medida que el compromiso de los profesores se haga más expreso y se recupere la vocación profesional, podremos tener aspiraciones de superación sustentadas en hechos y no en sueños. Ma. Guadalupe Flores Barrera y Andrés Rivera Díaz Coordinadores Estatales del Programa EMAyCIT-Hidalgo 8 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Programación Primer Grado. Biología ECAMM-HIDALGO SEPTIEMBRE Semana Bloque I. La biodiversidad: resultado de la evolución 1 2 3 4 Principales características que distinguen a los seres vivos. Importancia de la biodiversidad en la dinámica de los ecosistemas y en la atención de las necesidades del ser humano desde la perspectiva de desarrollo sustentable. Actividad Página La importancia de las gráficas (I) 12 La importancia de las gráficas (II) 16 Eras geológicas 20 Técnicas de fechamiento de fósiles (I) 24 OCTUBRE Semana Bloque I. La biodiversidad: resultado de la evolución Actividad Página 1 Técnicas de fechamiento de fósiles (II) 25 2 ¿Cuántas especies existen? 27 Crecimiento exponencial de células (I) 31 Crecimiento exponencial de células (II) 34 3 4 Implicaciones de la ciencia y la tecnología en el conocimiento y la conservación de la biodiversidad. Propuesta Hidalgo 1er Grado BIOLOGÍA 9 NOVIEMBRE Herramienta Semana Bloque II. La nutrición 1 Importancia de la nutrición en la obtención de energía y en la conservación de la salud. Dieta y actividad corporal (I) 36 2 Diversas formas de nutrición de los seres vivos y su relación con la adaptación. Dieta y actividad corporal (II) 40 Nutrición (I) 43 Nutrición (II) 47 3 4 Semana 1 2 Importancia de la tecnología en la producción de alimentos. DICIEMBRE Y ENERO Actividad Página Bloque II. La nutrición Aprovechamiento de recursos alimentarios con la aplicación de medidas para el cuidado y la conservación ambiental. Página Nutrición (III) 51 Bajar de peso = Alimento + ejercicio 53 La respiración como un fenómeno cíclico (I) 56 La respiración como un fenómeno cíclico (II) 58 Bloque III. La respiración 3 4 La respiración como proceso que caracteriza a todos los seres vivos. Datos sobre enfermedades respiratorias (I) Datos sobre enfermedades respiratorias (II) 5 Causas de las enfermedades respiratorias más frecuentes y cómo prevenirlas. 6 Semana 1 2 3 4 10 FEBRERO Actividad Bloque III. La respiración Distintas estructuras respiratorias como evidencias de la diversidad y adaptación de los seres vivos. Importancia histórica del desarrollo tecnológico en el tratamiento de las enfermedades respiratorias. 60 61 Página Escalas entre animales de diferentes tamaños (I) 62 Escalas entre animales de diferentes tamaños (II) 64 Datos sobre las drogas y el ritmo cardiaco (I) 68 Datos sobre las drogas y el ritmo cardiaco (II) 69 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Programación Biología Primer Grado ECAMM-HIDALGO Semana Bloque IV. La reproducción 1 La sexualidad humana desde una perspectiva amplia que involucra cuatro potencialidades: género, vínculos afectivos, erotismo y reproducción. 2 3 4 5 6 La reproducción del ser humano, al igual que en los diversos seres vivos, es resultado de un largo proceso evolutivo. La participación de la tecnología en los procesos de reproducción de plantas y animales. Semana Bloque V. Salud, ambiente y calidad de vida 1 2 3 4 Situaciones problemáticas o de interés personal, relacionadas con la biodiversidad, la nutrición, la respiración y la reproducción, mediante proyectos para integrar conocimientos, promover la salud y el cuidado del ambiente en favor de la calidad de vida. Semana Bloque V. Salud, ambiente y calidad de vida 1 2 3 4 Valor personal, social y cultural del conocimiento científico y tecnológico. MARZO Y ABRIL Actividad Página Los experimentos de Mendel (I) 71 Los experimentos de Mendel (lI) 77 Distribución genética (I) 78 Distribución genética (II) 82 ADN (ácido desoxirribonucleico) 84 ARN (ácido ribonucleico) 86 MAYO Actividad Página Distribución de edades en poblaciones 88 Epidemias 92 Competencia entre dos especies 97 Interacción depredador-presa 101 JUNIO Actividad Página Fibonacci y sus conejos 103 Temperatura corporal 105 Tipos sanguíneos (I) 107 Tipos sanguíneos (II) 111 Propuesta Hidalgo 1er Grado BIOLOGÍA 11 La importancia de las gráficas (I) ImportGrafs01 En esta serie de actividades usaremos tres tipos de gráficas para representar datos. Mostraremos cuál de los tipos es el más apropiado a cada situación. Observa los siguientes datos de 10 personas adultas: NOMBRE ALTURA (cm) PESO (kg) COLOR DE OJOS COLOR DE PELO Lan 175 75 Café Negro Bob 165 87 Negro Negro Rus 160 63 Azul Rubio Ena 75 32 Café Pelirrojo Cal 168 70 Café Negro Dil 167 100 Azul Café Ami 182 83 Negro Negro Shak 215 150 Café Negro Tes 150 50 Negro Café Iri 172 67 Café Negro ¿Qué podrías decir acerca de cada una de las cuatro características de este grupo de individuos? Altura: Peso: Color de ojos: Color de pelo: Veamos ahora cómo podemos presentar la información contenida en la tabla anterior para interpretarla mejor y sacar algunas conclusiones. Empecemos con el color de ojos. Completa la tabla siguiente anotando las cantidades (frecuencias) de cada color: COLOR DE OJOS CANTIDAD (FRECUENCIA) Negro 3 Café Azul 12 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Qué fracción de las personas del grupo tiene ojos cafés? ¿Qué porcentaje tiene ojos negros? Estas frecuencias se pueden representar en una gráfica circular como la siguiente. Azul 20% Negro 30% Café 50% Comprueba tus respuestas anteriores. Agrupa en la siguiente tabla de frecuencias los datos dados en la hoja anterior del color de pelo. En el círculo a su derecha, traza los sectores de cada color, señalando sus porcentajes correspondientes (el tamaño de cada sector lo puedes determinar estimando la porción que le corresponde). COLOR DE PELO CANTIDAD (FRECUENCIA) Negro Café Rubio Pelirrojo ¿Cuál es el color de pelo más frecuente? En tu salón de clase, ¿cuántos niños hay? ¿Cuántos de ellos tienen pelo negro? Propuesta Hidalgo 1er Grado BIOLOGÍA 13 Otro tipo de gráfica es la de columnas. Abajo tenemos representada la altura de cada persona del grupo en este tipo de gráfica. 250 Altura (cm) 200 150 100 50 0 Lan Bob Rus ¿Quién es el más alto? Ena Cal Dil Ami Shak Tes Iri ¿Quién es el más bajo? Aproximadamente, ¿cuál es la altura más representativa de este grupo de personas? Abajo a la izquierda haz una gráfica de columnas para los datos agrupados en frecuencias del color de ojos. En la derecha haz una gráfica de columnas para los datos agrupados en frecuencias del color de cabello. 6 6 5 5 4 4 3 3 2 2 1 1 0 14 Negro Café Azul 0 Negro Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Café Rubio Pelirrojo En el espacio de abajo traza la gráfica de columnas para el peso de cada persona del grupo dado en la primera hoja de esta actividad. Toma datos de tus compañeros de clase sobre alguna característica y represéntalos abajo en una gráfica (escoge el tipo de gráfica que creas más conveniente). Propuesta Hidalgo 1er Grado BIOLOGÍA 15 La importancia de las gráficas (II) ImportGrafs02 Esta actividad se centra en gráficas de líneas curvas para representar datos que varían en forma continua. La tabla siguiente da las longitudes y pesos promedios de bebés en Estados Unidos, desde el nacimiento hasta los tres años de edad. EDAD (MESES) LONGITUD (cm) PESO (kg) 0 50 3 3 59 5.400 6 66 7.200 9 71 8.600 12 74 9.600 15 78 10.300 18 81 10.800 21 84 11.400 24 87 11.900 27 89 12.400 30 91 12.900 33 93 13.400 36 95 13.900 En esta tabla se encuentra concentrada mucha información que extraeremos poco a poco (En las respuestas que darás a continuación, no se te olvide poner las unidades.) ¿Cuál es la estatura promedio de un bebé al nacer? ¿Cuál es el peso “normal” de un bebé al año de nacido? ¿Cuántos centímetros crece un bebé en sus primeros tres años de vida? Esto quiere decir que en estos primeros tres años, el bebé casi duplica su longitud. Aproximadamente, ¿cuántas veces incrementa el peso de un bebé en sus primeros tres años de vida? (Sugerencia: piensa en un bebé que nace con un peso de 3 kg y que a los tres años pesa 15 kg). 16 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Cuánto aumenta el peso de un bebé en su primer año? ¿Cuánto aumenta el peso de un bebé en su segundo año? ¿Cuánto aumenta el peso de un bebé en su tercer año? ¿En cuál periodo de tres meses se observa el incremento más rápido de peso de un bebé? En los siguientes dos planos coordenados traza las gráficas de la longitud y el peso como función de la edad. Primero representa cada uno de los datos de la tabla anterior con un punto y después conecta los puntos con una línea curva que pase por ellos. Longitud (cm) 100 90 80 70 60 50 40 30 20 10 0 0 3 6 9 12 15 18 21 24 27 30 33 36 Edad (meses) Peso (kg) 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 0 6 9 12 15 18 21 24 27 30 36 33 Edad (meses) 3 Propuesta Hidalgo 1er Grado BIOLOGÍA 17 Discute con tus compañeros de equipo cuándo se observa en las gráficas un crecimiento más rápido y cuándo un crecimiento más lento (Sugerencia: discute también por qué se deben conectar estos puntos con una línea curva. La tabla siguiente muestra la altura y peso promedios de mujeres y hombres en Estados Unidos, de tres a 18 años de edad. MUJER (VALORES PROMEDIO) HOMBRE (VALORES PROMEDIO) EDAD (AÑOS) ALTURA (cm) PESO (kg) ALTURA (cm) PESO (kg) 3 95 14 95 15 4 102 16 103 17 5 109 18 110 19 6 115 20 116 21 7 121 22 122 23 8 126 25 127 25.5 9 132 28.5 132 28 10 138 32 137 31.5 11 145 37 143 35.5 12 151 41.5 149 40 13 157 46.5 156 45 14 160 50 163 51 15 162 53.5 169 57 16 163 56 173 62.5 17 164 57 176 66.5 18 165 57 177 69 De acuerdo con la información presentada, contesta las siguientes preguntas. ¿Cuánto aumenta la altura de una mujer, de 3 a 4 años de edad? de 6 a 7 años? de 9 a 10 años? de 12 a 13 años? de 15 a 16 años? de 17 a 18 años? ¿Qué puedes deducir de estos valores? 18 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Cuánto aumenta la altura de un hombre, de 3 a 4 años de edad? de 6 a 7 años? de 9 a 10 años? de 12 a 13 años? de 15 a 16 años? de 17 a 18 años? ¿Qué puedes deducir al observar estos valores? ¿Cuál es la altura promedio (en Estados Unidos) para una mujer de tu edad? Mide la altura de cinco mujeres de tu clase. ¿Cuál es el promedio de estos cinco valores? Compara este valor con el de arriba. ¿Cuál es la altura promedio (en Estados Unidos) para un hombre de tu edad? Mide la altura de cinco hombres de tu clase. ¿Cuál es el promedio de estos cinco valores? Compara este valor con el de arriba. Tarea En papel cuadriculado y en los mismos ejes coordenados traza las gráficas de la altura promedio de una mujer y un hombre como función de la edad. Analiza las gráficas y escribe aquí tus observaciones. En papel cuadriculado y en los mismos ejes coordenados traza las gráficas del peso promedio de una mujer y un hombre como función de la edad. Analiza las gráficas y escribe aquí tus observaciones. Propuesta Hidalgo 1er Grado BIOLOGÍA 19 Eras geológicas ErasGeo En esta actividad continuaremos el estudio de los sucesos importantes en la historia de la Tierra. También introduciremos la división del tiempo geológico en eras y periodos. En la siguiente tabla hemos ordenado los sucesos enlistados en la actividad anterior, desde el más antiguo hasta el más reciente (compara con la lista que hiciste). Tienes que agregar ahora el tiempo aproximado en el que sucedió cada uno. Para esto, abre el archivo ErasGeo. En él encontrarás que el tiempo geológico se representa por el número de la fila en millones de años. Es decir, la fila 4 750 representa lo que sucedió hace 4 750 millones de años. En la columna C de la hoja están escritos algunos sucesos importantes, incluyendo los de la lista de abajo. Usando la barra de desplazamiento a la derecha de la hoja, sube progresivamente en el tiempo y encuentra los tiempos pedidos abajo: SUCESOS ORDENADOS DESDE EL MÁS ANTIGUO AL MÁS RECIENTE 1 Origen del Sistema Solar 2 Formación de la Tierra 3 Origen de la vida 4 Fósiles más antiguos 5 Origen de los organismos multicelulares 6 Fósiles más antiguos de animales 7 Primeros vertebrados 8 Aparecen los peces 9 Primeros insectos 10 Aparecen los reptiles 11 Primeros dinosaurios 12 Aparecen los mamíferos 13 Aparecen las aves 14 Primeros primates 15 Aparece el hombre TIEMPO APROXIMADO Explica cómo es posible que los fósiles más antiguos encontrados estén antes en la lista que el origen de los organismos multicelulares: 20 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Cuánto tiempo pasó desde el origen de la vida hasta el origen de los organismos multicelulares? ¿Cuánto tiempo pasó desde el origen de los organismos multicelulares hasta los primeros vertebrados? Para contestar las siguientes preguntas tendrás que obtener más información de la hoja de cálculo. ¿Aparecen los invertebrados antes o después de los vertebrados? ¿Cuántos millones de años aproximadamente pasaron de un suceso al otro? ¿Cuáles células aparecieron primero: las eucarióticas o las procarióticas? ¿Cuántos millones de años (aproximadamente) pasaron de un suceso al otro? El tiempo geológico está dividido en eras (y periodos dentro de estas eras) para marcar acontecimientos notables, como el desarrollo explosivo de nuevas formas de vida o extinciones masivas. Por ejemplo, en el periodo Cámbrico de la era Paleozoica tuvieron su origen muchas clases del reino animal ausentes anteriormente. En el periodo Pérmico de la misma era, se extinguieron una gran cantidad de especies terrestres y marinas, y se esparcieron los reptiles. En la siguiente tabla aparecen las cuatro eras geológicas con sus correspondientes periodos. Completa los años de inicio y terminación y escribe un hecho importante de cada periodo (apóyate en la información del programa). MILLONES DE AÑOS ERA Cenozoico PERIODO Cuaternario Terciario INICIO FINAL 2 0 65 2 245 208 570 510 UN EVENTO IMPORTANTE Cretácico Mesozoico Jurásico Triásico Pérmico Carbonífero Paleozoico Devónico Silúrico Ordovícico Cámbrico Precámbrico Proterozoico Arqueozoico Propuesta Hidalgo 1er Grado BIOLOGÍA 21 Explica por qué el inicio de todos los periodos tiene un número mayor que su final en la tabla de arriba: ¿Cuál fue el periodo más largo de la era Mesozoica? La columna C de la hoja de cálculo contiene otros datos interesantes. Extrae tres de ellos que todavía no se hayan discutido. Descríbelos abajo incluyendo su tiempo aproximado y su periodo y era respectivos. La siguiente gráfica muestra el porcentaje de dióxido de carbono (CO2) en la atmósfera desde hace 570 millones de años hasta la fecha. % CO2 25 20 15 10 5 600 500 400 300 200 100 0 Millones de años 22 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria 0 Nota que hace aproximadamente 470 millones de años (el pico más alto de la gráfica), el CO2 atmosférico empezó a reducirse de 22% a 1%. ¿Qué sucedió alrededor de esos años para que haya pasado esto? (Busca en la hoja de cálculo.) Nota también en la gráfica anterior que hace aproximadamente 270 millones de años, el CO2 atmosférico empezó nuevamente a elevarse hasta el segundo pico de 5%. ¿Qué sucedió alrededor de esos años para que haya pasado esto? (Busca en la hoja de cálculo.) Desde hace aproximadamente 220 millones de años, se ha venido reduciendo el dióxido de carbono en la atmósfera, como muestra la figura anterior. ¿Podrías explicar esto? Propuesta Hidalgo 1er Grado BIOLOGÍA 23 Técnicas de fechamiento de fósiles (I) TecFechaFosiles01 En esta actividad se explicará cómo se obtienen las cantidades restantes de elementos radiactivos a través del tiempo para el fechamiento de fósiles. Tomemos como ejemplo el carbono 14, el cual se desintegra aproximadamente 10% cada 1 000 años. Para realizar algunos cálculos, comencemos con una cantidad de 100 unidades de este isótopo radiactivo. De acuerdo con lo anterior, en los primeros 1 000 años se habrá desintegrado 10% de las 100 unidades, es decir, 10 unidades. Así, quedarán 100 - 10 = 90 unidades de este elemento 1 000 años después. Las cantidades para el siguiente periodo de 1 000 años (del año 1 000 al 2 000) se calculan como sigue: unidades Cantidad desintegrada = 10% de 90 unidades = Cantidad sobrante después de 2 000 años = 90 - 9 = unidades En la siguiente tabla se han organizado los resultados anteriores junto con los cálculos de otros dos periodos de 1 000 años. Comprueba los valores dados y calcula, usando el mismo procedimiento, las cantidades faltantes en la tabla. TIEMPO EN AÑOS CANTIDAD SOBRANTE CANTIDAD DESINTEGRADA 0 100.00 1 000 90.00 10.00 2 000 81.00 9.00 3 000 72.90 8.10 4 000 65.61 7.29 5 000 6 000 7 000 8 000 43.05 9 000 10 000 ¿Qué porcentaje de carbono 14 se encontrará después de 10 000 años? Si en un fósil se observa que su cantidad de carbono 14 se ha reducido 35%, ¿qué edad aproximada tendrá este fósil? Si en un fósil se observa que su cantidad de carbono 14 se ha reducido 20%, ¿qué edad aproximada tendrá este fósil? (Sugerencia: continúa los cálculos de la tabla anterior hasta llegar a este porcentaje.) 24 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Técnicas de fechamiento de fósiles (II) TecFechaFosiles02 En esta actividad obtendremos en computadora las cantidades restantes de elementos radiactivos a través del tiempo para el fechamiento de fósiles. Trabajaremos con el carbono 14 y el uranio 238. Empecemos con el carbono 14, el cual, como mencionamos en la actividad anterior, se desintegra aproximadamente 10% cada 1 000 años. Este periodo de tiempo de 1 000 años es muy largo para observaciones de tiempo más cortas, así que conviene reducirlo. Este elemento radioactivo se desintegra 1.23% cada 100 años. Los cálculos para este intervalo se vuelven más tediosos pero podemos usar una computadora. Construye una hoja de cálculo como la siguiente. Las cantidades en las celdas A3, C2 y B3 necesitan fórmulas para ser copiadas hacia abajo posteriormente (para deducir las fórmulas, apóyate en los cálculos realizados en la actividad anterior). C2 A B C 1 TIEMPO EN AÑOS CANTIDAD SOBRANTE CANTIDAD DESINTEGRADA 2 0 100.00 3 100 98.77 1.23 4 200 97.56 1.21 5 300 96.36 1.20 6 400 95.17 1.19 C3 = 0.0123 Copia las tres columnas hacia abajo hasta que encuentres la vida media del carbono 14 (recuerda que ésta es el tiempo en el que la cantidad del elemento se reduce a la mitad). ¿En cuántos años se reduce 25% el carbono 14? años. Supón que se encuentra un fósil de una concha que contiene solamente el 5% restante de carbono 14. ¿Cuál sería la edad de esta concha? Un espécimen hallado en los restos de una civilización antigua contiene tan sólo 1% de carbono 14. ¿Qué edad le puedes atribuir a estos restos? Propuesta Hidalgo 1er Grado BIOLOGÍA 25 Compara las dos respuestas anteriores con las de la primera parte de esta actividad. Discute con tus compañeros las dos preguntas siguientes y escribe tus comentarios abajo. ¿Hasta qué tiempo máximo puede utilizarse el carbono 14 para establecer edades de fósiles? ¿Se acabará completamente la cantidad de carbono 14 en algún momento? Construye ahora una hoja de cálculo similar a la anterior para el uranio 238. Este elemento radiactivo se desintegra 0.154% cada 10 millones de años. C2 A B C 1 TIEMPO EN MILLONES DE AÑOS CANTIDAD SOBRANTE CANTIDAD DESINTEGRADA 2 0 100.000 3 10 99.846 0.154 4 20 99.692 0.154 5 30 99.539 0.153 6 40 99.385 0.153 C3 = 0.00154 ¿En cuántos millones de años se reduce el uranio 238 a 90%? millones de años. ¿En cuántos millones de años se reduce el uranio 238 a 80%? millones de años. ¿Obtén la vida media del uranio 238? millones de años. En sedimentos muy antiguos se hallaron fósiles de algunas células con núcleo. Si se encontró un nivel de 77% en el uranio 238 presente, ¿cuál es la edad de estas células? En sedimentos todavía más antiguos se hallaron fósiles de algunas células sin núcleo. Si se encontró un nivel de 58% en el uranio 238 presente, ¿cuál es la edad de estas células? 26 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Cuántas especies existen? EspeciesExisten En esta actividad daremos una idea de la cantidad de especies diferentes que existen en la naturaleza. También clasificaremos estas especies de acuerdo con su reino, su filum y su clase. En una revista apareció la siguiente información sobre la cantidad de especies que han sido clasificadas en los siguientes 18 grupos de seres vivos: 1. Bacterias y arqueos 4 mil 10. Insectos y miriápodos 963 mil 2. Protozoos y algas 80 mil 11. Gusanos nemátodos 25 mil 3. Hongos y líquenes 100 mil 12. Gusanos anélidos 12 mil 4. Plantas 270 mil 13. Quelicerados 75 mil 5. Aves 10 mil 14. Moluscos 70 mil 6. Peces 22 mil 15. Crustáceos 40 mil 7. Reptiles 7 mil 500 16. Platelmintos 20 mil 8. Anfibios 3 mil 17. Cnidarios 10 mil 9. Mamíferos 4 mil 500 18. Esponjas 10 mil Además, el mismo artículo menciona que se han clasificado 10 mil especies más en grupos de organismos diversos. ¿Cuántas especies en total se han clasificado hasta la fecha? Es evidente que el grupo de “Insectos y miriápodos” (ciempiés, milpiés) es el que tiene más especies clasificadas. ¿Qué porcentaje de las especies clasificadas pertenece a este grupo? (Procedimiento: divide 963 entre 1 726 y multiplícalo por 100.) Escribe abajo los cinco grupos que contienen el mayor número de especies clasificadas, junto con sus cantidades correspondientes: 1º Insectos y miriápodos 963 mil 2º 3º 4º 5º Propuesta Hidalgo 1er Grado BIOLOGÍA 27 El último grupo que escribiste, los “Quelicerados”, se refiere a las arañas y escorpiones. ¿A qué conclusión puedes llegar después de observar estos cinco grupos más dominantes? Los seres vivos están clasificados en cinco reinos: Monera, Protista, Fungi, Plantae y Animalia. En la primera tabla dada, el primer grupo (el 1) representa al reino Monera, el segundo grupo (el 2) al reino Protista, el tercer grupo (el 3) al reino Fungi y el cuarto grupo (el 4) al reino Plantae. Todos los demás pertenecen al reino Animalia. De acuerdo con esto, llena la siguiente tabla con las cantidades de especies que pertenecen a cada uno de los reinos. Monera Protista Fungi Plantae Animalia En la siguiente gráfica circular representamos estas cantidades de especies clasificadas en cada reino. 5% Protista 0% Monera 6% Fungi 16% Plantae 73% Animalia 28 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Al reino Monera (organismos unicelulares que carecen de núcleo) le corresponde sólo el 0.23% (0% en la gráfica). ¿Por qué crees que este grupo tenga un porcentaje tan bajo de especies clasificadas? ¿Qué porcentaje le corresponde al reino Animalia? ¿Qué porcentaje le corresponde al reino Plantae? ¿Por qué crees que estos dos grupos sean los que tienen más especies clasificadas? El reino animal se divide a menudo en dos grandes grupos: los vertebrados y los invertebrados. Los vertebrados comprenden cinco clases diferentes: los peces, los anfibios, los reptiles, las aves y los mamíferos. Extrae de la tabla original estas cinco clases de vertebrados y ordénalos de acuerdo con el número de especies que tienen clasificadas. Peces 22 mil ¿Cuántas especies hay clasificadas en el grupo de los vertebrados? Propuesta Hidalgo 1er Grado BIOLOGÍA 29 En la siguiente figura representa estas cinco clases en una gráfica circular. (Sugerencia: los porcentajes correspondientes a cada clase son: peces, 47%; aves, 21%; reptiles, 16%; mamíferos, 10%; y anfibios, 6%. Con base en estos valores, estima el tamaño del sector que le corresponde a cada uno.) Escribe enseguida algunas conclusiones sobre los resultados anteriores: 30 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Crecimiento exponencial de células (I) CrecExpCelulas01 En esta actividad estudiaremos el “crecimiento de células”, es decir, los cambios en la cantidad de células y no en su tamaño. La microbiología estudia en el laboratorio el crecimiento de microbios o microorganismos en cultivo. Éstos son organismos vivientes muy pequeños, formados por una sola célula. Un método muy común por el cual las células se reproducen y aumentan en número es la llamada “fisión binaria”. Ésta consiste en la división de una célula en dos. Usaremos aquí esta idea en una simulación, para observar el crecimiento de un agregado celular. Toma una hoja de papel y corta 20 papelitos pequeños (éstos serán tus células o tus microbios). Vamos a suponer que se reproduce una quinta parte de estas células. Con tus papelitos forma cinco montones iguales (cada uno representa la quinta parte). Las células de uno de los montones (escoge el que quieras) se reproducirán. Para esto, cuenta cuántos papelitos hay en ese montón y agrega esta cantidad de nuevos papelitos al montón (es decir, había cuatro células que al reproducirse por división formarán en total ocho células). Como sabes, las células se seguirán reproduciendo, así que tenemos que repetir el procedimiento anterior una y otra vez. Seguiremos suponiendo que una quinta parte de las células se reproducen (a esta propiedad se le conoce como tasa de crecimiento). A continuación te damos los pasos a seguir. Junta nuevamente todos los papelitos. Con los papelitos que quedaron forma cinco montones más o menos iguales (cada uno representa la quinta parte). Las células de uno de los montones se reproducirán (escoge el que quieras). Cuenta cuántos papelitos hay en ese montón y agrega esta cantidad de nuevos papelitos al montón. Repite el procedimiento anterior una y otra vez y ve llenando la siguiente tabla. Propuesta Hidalgo 1er Grado BIOLOGÍA 31 NÚM. DE REPETICIÓN CANTIDAD DE PAPELITOS AGREGADOS 1 4 2 3 4 5 6 7 8 9 10 Extiende esta tabla lo más que puedas En la décima repetición del procedimiento que seguiste, debió haber alrededor de 100 papelitos y tuviste que haber agregado alrededor de 20 papelitos (la quinta parte se reproduce). Imaginemos que continuamos con este proceso. Cuando se lleguen a tener 500 papelitos, ¿cuántos tendrías que agregar? Cuando se lleguen a tener 1 000 papelitos, ¿cuántos tendrías que agregar? ¿Por qué agregas cada vez una mayor cantidad de papelitos? Pasemos a una situación similar, pero en vez de usar papelitos, hagamos los cálculos correspondientes. Supongamos que tenemos en cultivo una cantidad inicial de 16 000 microorganismos y que su tasa de crecimiento es de 0.5 por hora. Esto quiere decir que la mitad (0.5) de los organismos se reproducirán cada hora. Así tendremos que: Cantidad de microorganismos que se reproducen al inicio = 0.5 × (16 000) = 8 000 Cantidad total de microorganismos en la primera hora = 16 000 + 8 000 = 24 000 Si repetimos estos cálculos una vez más, obtendremos los resultados de la tabla siguiente. Explica los valores de 12 000 y 36 000 en ella y continúa llenando la tabla hasta el final, utilizando el mismo procedimiento (si lo haces correctamente, debes llegar al valor de 27 000 indicado en la tabla). 32 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria TIEMPO (HORAS) CANTIDAD TOTAL DE MICROORGANISMOS CANTIDAD EN QUE SE REPRODUCEN 0 16 000 0 1 24 000 8 000 2 36 000 12 000 3 4 27 000 5 6 El crecimiento que se observa en la tabla anterior es del tipo llamado exponencial. En él, la cantidad de microbios aumenta proporcionalmente a la cantidad presente, de acuerdo con una tasa de crecimiento. Esto se observa frecuentemente en poblaciones de individuos, ya que lógicamente una población dos veces mayor debe incrementarse al doble si tiene las condiciones favorables. En una población de 10 000 personas, se observaron 500 nacimientos en un año. En otra población similar de 20 000 personas, ¿cuántos nacimientos esperarías que hubiera en el mismo año? Discute estas ideas con tu profesor y tus compañeros. Propuesta Hidalgo 1er Grado BIOLOGÍA 33 Crecimiento exponencial de células (II) CrecExpCelulas02 En la actividad anterior empezamos a estudiar el “crecimiento celular”. En esta segunda actividad ampliaremos estas ideas. La bacteria Escherichia coli (E. coli) habita en el sistema intestinal del hombre y de otros animales. En su ambiente normal no es patógena. ¿Qué quiere decir “no patógena”? En un cultivo de esta bacteria, se realizaron las siguientes observaciones: TIEMPO (HORAS) CANTIDAD DE E. COLI (EN MILLONES) 0 10 1 20 2 39 3 76 4 150 5 290 6 560 7 1100 8 1800 Observarás que la cantidad de esta bacteria se duplicó (de 10 a 20 millones) en la primera hora. Así, podemos suponer que ésta es su rapidez de crecimiento natural. Completa la siguiente tabla siguiendo esta idea de duplicación por cada hora. TIEMPO (HORAS) CANTIDAD DE E. COLI (EN MILLONES) 0 10 1 20 2 40 3 80 4 5 6 7 34 8 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria En los siguientes ejes coordenados, traza las gráficas de las dos variaciones anteriores: la primera tabla de observaciones y la segunda tabla de cálculos (indícalas claramente). Para ayudarte a hacer esto, hemos trazado estas gráficas hasta la cuarta hora (ambas gráficas resultan iguales hasta este tiempo). Cantidad (en millones) 3 000 2 750 2 500 2 250 2 000 1 750 1 500 1 250 1 000 750 500 250 0 0 1 2 3 4 5 6 7 8 Tiempo (horas) La gráfica de los cálculos, de acuerdo con un modelo exponencial (duplicación cada hora), se despega de la otra, conforme avanza el tiempo. Esto quiere decir que el modelo exponencial es un buen predictor para la primera etapa del crecimiento, pero no para la segunda. En el espacio de abajo escribe tus ideas acerca de por qué el crecimiento de las bacterias se va alejando de un crecimiento puramente exponencial (es decir, hay algo que va limitando su crecimiento). Cuando termines, discute tus ideas con todo tu grupo. Propuesta Hidalgo 1er Grado BIOLOGÍA 35 Dieta y actividad corporal (I) DietActiCorporal01 En esta actividad hablaremos del contenido energético de algunos alimentos y del gasto energético en algunas actividades. El contenido energético de un alimento depende de la cantidad de éste. Observa la siguiente tabla que indica el contenido energético de las nueces para diferentes cantidades ingeridas. CANTIDAD (g) ENERGÍA (kJ) 50 1 450 200 5 800 600 17 400 En cada caso de la tabla anterior, divide la “Energía” entre la “Cantidad” para encontrar la energía contenida en un gramo de nuez: kJ por gramo. ¿Cuánta energía contendrán 100 gramos de nueces? kJ. Este contenido energético se expresa también como “2 900 kJ por 100 gramos” (2 900 kJ/100 g). La siguiente tabla contiene la energía aproximada que proporcionan 100 gramos de diferentes alimentos (en una actividad posterior explicaremos cómo se obtiene ese dato.) ALIMENTO 36 ENERGÍA (kJ/100g) ALIMENTO ENERGÍA (kJ/100g) Nueces 2 900 Naranja 200 Pan blanco 1 100 Carne de res 700 800 Leche 300 Helado Huevo 700 Queso amarillo 1 700 Tortilla 1 000 Chocolate 2 200 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Cuáles son los tres alimentos de la lista con mayor contenido energético? ¿Cuánta energía contiene un helado de 250 g? (Sugerencia: 250 g son dos veces y media 100 g.) Supón que en un desayuno consumes los siguientes alimentos en las cantidades que aparecen en la tabla. Calcula la energía proporcionada por cada alimento y la energía total ingerida. ALIMENTO CANTIDAD (g) Naranja 200 Huevo 50 Tortilla 150 Leche 200 ENERGÍA (kJ) ENERGÍA TOTAL La energía de cualquier tipo se expresa en joules o kilojoules. En nutrición, sin embargo, se utiliza más frecuentemente otra unidad llamada “Caloría” (la letra mayúscula inicial indica que esta unidad representa 1 000 calorías tal y como se definen en física). La equivalencia entre kilojoules y calorías es la siguiente: 1 Caloría 4.2 kilojoules (aproximadamente) Lo anterior significa que para convertir kilojoules a calorías hay que dividir entre 4.2. Completa la tabla siguiente convirtiendo el valor energético de cada alimento (kJ/100g) a su valor en calorías por cada 100 gramos (Cal/100g). Redondea los valores a enteros. ALIMENTO ENERGÍA (kJ/100g) Nueces 2 900 Pan blanco 1 100 Leche 300 Huevo 700 Tortilla 1 000 ENERGÍA (Cal/100g) 690 167 ALIMENTO ENERGÍA (kJ/100g) Naranja 200 Carne de res 700 Helado 800 Queso 1 700 Chocolate 2 200 ENERGÍA (Cal/100g) Propuesta Hidalgo 1er Grado BIOLOGÍA 37 La energía que se consume en una actividad depende del tiempo que dure la misma. Observa la siguiente tabla, que contiene la energía total que ha consumido un joven de 15 años al correr durante varias horas. Complétala de acuerdo con los dos primeros valores dados. TIEMPO (hrs) ENERGÍA CONSUMIDA (kJ) ___ 1 125 1 2 250 1 ___ 2 ¿Cuánta energía consume al correr en cada hora? ¿A cuántas calorías equivale esta energía? Como puedes observar en la tabla, al correr durante dos horas, este joven consume 4 500 kJ o 1 070 Cal, aproximadamente. Para reponer esta energía, ¿cuántos gramos de pan blanco debe comer este joven? O ¿cuántos gramos de leche debe comer este joven? Este kilo y medio de leche representa un litro y medio. Un joven de 15 años tiene un gasto energético base de 240 kJ por hora. Esto, como recordarás, quiere decir que, incluso dormido, su cuerpo consume 240 kJ cada hora (a este gasto de base se le conoce como “Requerimiento energético basal”). Así, la energía extra consumida al correr por cada hora sería de 2 250 — 240 = En la tabla siguiente se muestran las energías que consume por hora un joven de 15 años en algunas actividades. Réstales 240 kJ para encontrar la energía extra gastada. ACTIVIDAD (kJ/hr) 38 ENERGÍA TOTAL (kJ/hr) Dormir 240 Sentarse 340 Caminar 630 Nadar 1 640 Correr 2 250 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ENERGÍA EXTRA 390 2 010 ¿Por qué la energía extra al dormir es de cero? Supón que en un día escolar de 6 horas llevas a cabo las siguientes actividades en los intervalos de tiempo que aparecen en la tabla. Calcula el gasto de energía de cada actividad y la pérdida total de energía durante estas 6 horas (utiliza las energías totales de cada actividad que se encuentran en la última columna de la tabla anterior). ACTIVIDAD Sentado TIEMPO (hrs) GASTO DE ENERGÍA (kJ) 4 ___ Caminando ___ Corriendo 1 GASTO TOTAL ¿Cuál es el gasto total en calorías? Escribe a continuación un resumen breve de los puntos más importantes que aprendiste en esta actividad. Posteriormente discútelos con todo tu grupo. Propuesta Hidalgo 1er Grado BIOLOGÍA 39 Dieta y actividad corporal (II) DietActiCorporal02 En actividades anteriores hablamos del contenido energético de algunos alimentos y del gasto energético en algunas actividades corporales. En esta actividad profundizaremos sobre estos temas por medio del programa de cómputo. Abre el archivo DietActiCorporal02. En la parte superior se piden los datos de la persona ya que el gasto energético varía con la edad, el peso, la altura y el sexo. Para mostrar esto, en cada uno de los cuatro sujetos de la tabla siguiente, introduce en el programa sus datos y obtén su “Requerimiento energético basal” (que está en color rosa en la parte superior derecha de la pantalla) y su “Energía consumida extra” durante dos horas de caminata (que aparece en la columna amarilla de la pantalla). Observa el primer ejemplo. DATOS DEL SUJETO SEXO EDAD PESO (kg) ALTURA (m) REQUERIMIENTO ENERGÉTICO BASAL (Cal) F 15 45 1.55 1 295 M 15 45 1.55 F 30 90 1.70 M 30 90 1.70 ENERGÍA CONSUMIDA EXTRA (Cal) 2 HORAS DE CAMINATA 176 ¿Qué puedes concluir acerca de los valores obtenidos en la tabla anterior? Introduce en el programa los datos personales del primer sujeto de arriba con un requerimiento energético basal de 1 295 Cal. En la sección amarilla se distribuyen las actividades de la persona durante el día: 8 horas de sueño, 1 de estar despierto (acostado), 4 de estar sentado, 4 de estudiar, etcétera (nota que los tiempos suman en total las 24 horas del día). 40 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Observa, por ejemplo, que gastó 92 Cal extras al estar sentado 4 horas. ¿Cuántas Cal extras gastó por hora en esta actividad? ¿Gasta más o menos Cal al estar de pie durante una hora? ¿Cuántas Cal extras gasta por hora al caminar? ¿Cuántas Cal extras gasta por hora al correr? Aproximadamente, ¿cuántas veces más se gasta de energía al correr que al caminar? En la parte inferior de las columnas de “Energía consumida extra” aparecen los totales. ¿Cuál es el total de la energía consumida extra en calorías? En la parte superior, con letra amarilla, bajo el nombre “Energía necesaria total”, el programa suma la energía basal y la extra. ¿Cuánto dio esta energía en calorías? Ésta es la energía total gastada por el cuerpo y, por lo tanto, tiene que ser suministrada en forma de alimentos. Observa ahora la sección verde, donde aparecen los alimentos que consumió durante el día. Aun cuando en el programa no se muestran en orden, desayunó un jugo de naranja, 2 huevos y 5 tortillas; comió un plato de arroz con chícharos, carne de res y un pan; y cenó una torta de queso amarillo, leche de chocolate y 2 galletas. Señala tres de estos alimentos que le proporcionaron mayor energía y escríbelos en las líneas de abajo. (Ve la última columna de “Energía”.) En la parte superior, con todos los totales, está la “Energía proporcionada” en color verde con letras rojas. ¿Cuál es el valor total de esta energía proporcionada por los alimentos? Debajo de este valor (en blanco) Está el valor de la “Diferencia”. Deduce y explica a continuación de dónde surge esta diferencia y por qué su valor es negativo. Ya te diste una idea de lo que contiene este programa. Ahora te toca usarlo siguiendo las instrucciones. Propuesta Hidalgo 1er Grado BIOLOGÍA 41 Introduce en el programa los datos personales de alguno de ustedes (si no sabes el peso o la altura, estímalos). ¿Cuál es su requerimiento energético basal correspondiente en calorías? Pasa a la sección amarilla donde se distribuyen las actividades del día. Borra los tiempos dados con el botón “V Borrar V”. Representa un día completo de actividades, escribiendo en el programa los tiempos que dedicarías a cada una (la suma debe ser igual a 24). ¿Cuál fue la actividad que consumió más energía? ¿Cuánto tiempo le dedicaste? ¿Cuánta energía extra se gastó en ella (en calorías)? Calcula cuánta energía extra se gasta por hora en esta actividad. En la parte inferior de las columnas de “Energía consumida extra” se ofrecen los totales. ¿Cuál fue el total en calorías de la energía extra consumida? ¿Cuál es la “Energía necesaria total” en calorías? (Este valor aparece en la parte superior con letra amarilla.) Explica qué representa este valor: Para balancear esta energía, tienes que definir una alimentación durante el día. Para hacer esto, pasa a la sección verde y borra los datos con el botón “V Borrar V”. Planea tu alimentación del día introduciendo, en la columna correspondiente, el “Número de porciones” de cada alimento que piensas consumir. Trata de que el valor de la “Diferencia” entre la energía consumida y la proporcionada por los alimentos sea lo más cercana a cero. Escribe, en una hoja aparte, un pequeño reporte de las actividades que escogiste en el programa, los alimentos que tomaste en el día para balancear la energía perdida. Acompaña esto con sus cantidades respectivas y los totales de la energía consumida. Imagina ahora una persona obesa que casi no hace ejercicio y que come mucho. Inventa sus datos personales, sus actividades y sus alimentos ingeridos durante el día. Escribe un pequeño reporte de las actividades que escogiste para ella y los alimentos que ingirió durante el día. Acompaña esto con sus cantidades respectivas y los totales de energía consumida (presenta después tus resultados a todo el grupo). 42 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Nutrición (I) Nutricion01 En esta serie de actividades hablaremos de la importancia de una dieta balanceada. Nos concentraremos en su contenido de carbohidratos, lípidos y proteínas. Una dieta balanceada debe contener los cinco constituyentes: carbohidratos, lípidos, proteínas, vitaminas y minerales. Observa la siguiente tabla proporcionada en un paquete de pastas secas donde aparece su información nutrimental. PORCIÓN CONTENIDO ENERGÉTICO Proteínas 39 g 150 Cal 5g Grasas (lípidos) 2.5 g 4% * Carbohidratos 26 g 9% * Sodio 0.8 g 32% * Vitamina A 40% * Vitamina C 15% * Hierro 8% * *Porcentaje del consumo diario recomendado ¿Contiene esta pasta los cinco constituyentes? ¿De cuál contiene más? ¿Cuál es el porcentaje de carbohidratos en la pasta? (26 de 39 g) El contenido energético se calcula sobre la base de la siguiente información: Aproximadamente, cada gramo de proteínas proporciona 4 calorías, cada gramo de grasas proporciona 9 calorías y cada gramo de carbohidratos proporciona 4 calorías. Propuesta Hidalgo 1er Grado BIOLOGÍA 43 Usando estos datos y los valores de la tabla anterior, completa los dos valores que faltan para establecer el contenido energético de una porción de pasta. calorías de proteínas = 4 × 5 = 20 Cal calorías de grasa = 9 × = 22.5 Cal calorías de carbohidratos = 4 × 26 = Cal calorías totales = 146.5 Cal Compara este valor con el del paquete de pastas (ambos son valores aproximados): Nota que la pasta contiene más gramos de proteínas (5 g) que de grasas (2.5 g). ¿Por qué, entonces, hay más calorías de la grasa (22.5) que de las proteínas (20)? La siguiente información nutrimental se obtuvo de un frasco de aderezo para ensaladas, de una caja de galletas de trigo y de una lata de atún. ADEREZO PARA ENSALADAS Porción GALLETAS DE TRIGO LATA DE ATÚN 15 g 30 g 170 g 43 Cal 131 Cal 111 Cal 0g 3g 24.2 g Grasas 3.8 g 3.6 g 0.8 g Carbohidratos 2.1 g 21 g 1.8 g 170 mg 204 mg 0.3 g Contenido energético Proteínas Sodio El aderezo para ensaladas ¿contiene más proteínas, grasas o carbohidratos? Las galletas de trigo ¿contienen más proteínas, grasas o carbohidratos? 44 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria La lata de atún ¿contiene más proteínas, grasas o carbohidratos? ¿Cuál de los tres productos contiene más sodio? ¿Qué porcentaje de grasas contiene el aderezo para ensaladas? (Sugerencia: usa una calculadora para dividir 3.8 entre 15 y multiplicar el resultado por 100.) ¿Qué porcentaje de carbohidratos contienen las galletas de trigo? ¿Qué porcentaje de proteínas contiene el atún en lata? Generalizando los resultados anteriores podrías decir qué alimentos son ricos en: Grasas: Carbohidratos: Proteínas: Completa lo siguiente para calcular el contenido energético de una porción de atún: calorías de proteínas = 4 × 24.2 = Cal calorías de grasa = 9 × = Cal = Cal = Cal calorías de carbohidratos = 4 × calorías totales Compara con los datos de la tabla (deben ser muy similares). Observa ahora la parte superior de la tabla anterior, la cual aparece a continuación. ADEREZO PARA ENSALADAS Porción Contenido energético GALLETAS DE TRIGO LATA DE ATÚN 15 g 30 g 170 g 43 Cal 131 Cal 111 Cal Propuesta Hidalgo 1er Grado BIOLOGÍA 45 Supón que necesitas reponer aproximadamente 800 calorías que perdiste corriendo durante una hora. ¿Cuántos gramos de atún necesitarías? (Sugerencia: Estima primero la cantidad de porciones que necesitas. Realiza tus cálculos en el espacio que sigue.) ¿Cuántos gramos de galletas necesitarías? (Sugerencia: Estima primero la cantidad de porciones que necesitas. Realiza tus cálculos en el espacio que sigue.) A partir de los datos del tamaño de la porción y contenido energético dados en la tabla, calcula lo siguiente: ¿Cuántas calorías por gramo proporciona el aderezo para ensalada? ¿Cuántas calorías por gramo proporcionan las galletas de trigo? ¿Cuántas calorías por gramo proporciona el atún en lata? Según los resultados anteriores, ¿qué tipo de productos convendría comer para reponer la energía perdida en alguna actividad física? 46 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Nutrición (II) Nutricion02 En esta actividad usaremos un programa de cómputo que incluye el contenido de carbohidratos, lípidos y proteínas de varios alimentos. Esto nos ayudará a decidir qué grupos de alimentos son ricos en estos constituyentes y obtener una clasificación de ellos. Abre el archivo Nutricion02. Allí aparece una lista de alimentos con su porcentaje de proteínas, grasas y carbohidratos. También cada uno cuenta con la energía que suministra en calorías y kilojoules por 100 gramos y su “Grupo”. En la parte superior podrás ver seis botones, uno por cada categoría, que te permiten “Ordenar” los alimentos de acuerdo con esa propiedad. Haz “clic” en el botón verde que está arriba de la columna del “Porcentaje de proteínas”. Escribe abajo los primeros 10 alimentos de la lista más ricos en proteínas. NOMBRE DEL ALIMENTO % DE PROTEÍNAS Observa también los siguientes 10 alimentos de la lista para contestar lo siguiente. ¿Qué tipos de alimentos son los que contienen un gran porcentaje de proteínas? Propuesta Hidalgo 1er Grado BIOLOGÍA 47 Compara los porcentajes del “Atún enlatado” y las “Sardinas en aceite” con los del “Bacalao” y el “Camarón”. Explica las diferencias en grasa: Baja ahora para ver los alimentos con menor contenido de proteínas en la lista. ¿Qué tipos de alimentos son? Observa el contenido de algunas frutas. Nota que la suma de sus tres porcentajes es mucho menor a 100%. ¿Qué más contienen las frutas? Haz “clic” en el botón amarillo que está arriba de la columna de “Porcentaje de grasa”. Escribe abajo los primeros 10 alimentos de la lista con mayor porcentaje de grasa. NOMBRE DEL ALIMENTO % DE GRASA Observa también los siguientes 10 alimentos de la lista para contestar lo siguiente. ¿Qué tipos de alimentos son los que contienen un gran porcentaje de grasa? 48 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Baja ahora para ver los alimentos con menor contenido de grasa en la lista. ¿Qué tipos de alimentos son? Haz “clic” en el botón rojo oscuro que aparece arriba de la columna del “Porcentaje de carbohidratos”. Escribe abajo los primeros 10 alimentos de la lista con mayor porcentaje: NOMBRE DEL ALIMENTO % DE CARBOHIDRATOS Observa también los siguientes 10 alimentos de la lista para contestar lo siguiente. ¿Qué tipos de alimentos son los que contienen un gran porcentaje de carbohidratos? Baja ahora para ver los alimentos con menor contenido de carbohidratos en la lista. ¿Qué tipos de alimentos son? Propuesta Hidalgo 1er Grado BIOLOGÍA 49 Ordena ahora los alimentos por su última categoría: el grupo. Escribe abajo lo que representa cada grupo. Grupo I: Grupo II: Grupo III: La mayoría de estos alimentos tienen una clave en la última columna (P, V, C, F y QL). Por ejemplo, la P es para pescados. Viendo los alimentos correspondientes, adivina qué significa cada una de las otras claves y escríbelo abajo: V: C: F: QL: Trata de relacionar los tres grupos anteriores con las listas de alimentos con mayor contenido de proteínas, grasa y carbohidratos. Escribe tus conclusiones. 50 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Nutrición (III) Nutricion03 En esta actividad usaremos el programa de cómputo que incluye el contenido de carbohidratos, lípidos y proteínas de varios alimentos. Esto nos ayudará a diseñar una dieta balanceada. Los rangos sugeridos de estos tres componentes en la dieta de una persona adulta son los siguientes: Carbohidratos Lípidos Proteínas entre 55% y 70% entre 20% y 30% entre 10% y 15% El siguiente diagrama ilustra esta proporción en forma de alimentos y las porciones sugeridas. 2-4 porciones 5- 11 po rc es io ne s 3 2- n cio r po Abre el archivo Nutricion03 y pasa a su “Hoja2”. Allí, con base en las porciones, se puede escoger una comida para observar en la parte superior su contenido total en proteínas, grasa, carbohidratos, calorías y su masa. Por ejemplo, si observas las porciones elegidas, hemos representado una comida que consiste en una torta de jamón con queso amarillo, papas fritas y un refresco (la torta contiene una rebanada de jitomate, un poco de frijoles y mantequilla). ¿Qué porción de jitomate se eligió? Propuesta Hidalgo 1er Grado BIOLOGÍA 51 Explica esto, notando que la masa de la porción de jitomate es de 100 gramos: Observa la franja de “Totales” y contesta las siguientes preguntas: ¿qué masa total tiene esta comida? ¿Cuántas calorías contiene? Notarás que los porcentajes totales de proteínas, grasa y carbohidratos tienen dos números cada uno. El de arriba corresponde al porcentaje de la masa total de la comida. Por ejemplo, esta comida contiene 7% de proteínas de su masa total de 540 gramos. El número de abajo corresponde al porcentaje relativo entre los tres componentes: proteínas, grasa y carbohidratos. De estos tres componentes, 24% son proteínas, % grasa y % carbohidratos. Suma estos tres números para comprobar que completan 100%. De acuerdo con los porcentajes anteriores y los rangos dados en la página anterior, ¿está balanceada la comida anterior? Explica: Te toca diseñar ahora una comida balanceada. Para esto, borra el número de porciones que trae el programa, haciendo “clic” en el botón correspondiente. Introduce las porciones en el programa y analiza sus totales. Tienes que prestar atención a la masa de una porción dada en el programa (columna verde) y elegir la proporción correcta utilizada (si notaste, arriba se eligió para el jitomate una porción de 0.1 que representa una rebanada). Escribe a continuación los alimentos que elegiste con sus porciones correspondientes. NOMBRE DEL ALIMENTO 52 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria NÚM. DE PORCIONES Bajar de peso = alimento + ejercicio BajaPesoAlimEjer En esta actividad analizaremos las gráficas de la pérdida de peso de una persona bajo varios regímenes dietéticos y de ejercicio. Las ganancias y pérdidas de energía del cuerpo se miden en calorías (Cal). Los alimentos proporcionan calorías al cuerpo. El ejercicio hace que se quemen calorías. Una persona mantiene su peso si estos dos mecanismos se balancean el uno al otro. ¿Qué crees que suceda si una persona come más calorías de las que quema? ¿Qué debe hacer una persona si quiere perder peso? En la gráfica de abajo se representan los resultados de aplicar a cuatro personas (A, B, C y D) los siguientes planes para bajar de peso: A Reducir la alimentación para suministrar al cuerpo 500 Cal menos al día. B Incrementar la actividad para quemar 500 Cal extras diarias. C Reducir la alimentación en 500 Cal al día e incrementar la actividad para quemar otras 500 Cal diarias. D Reducir la alimentación en 500 Cal al día e incrementar la actividad para quemar otras 1 000 Cal diarias. Peso (kg) 128 A B C D 120 112 104 96 88 80 72 64 0 4 8 12 16 24 20 Tiempo (semanas) Propuesta Hidalgo 1er Grado BIOLOGÍA 53 ¿Cuál es el peso inicial de la persona A? ¿A qué peso llegó después de 16 semanas de dieta? ¿Cuántos kg perdió en estas 16 semanas? ¿Cuántos kg estuvo perdiendo por semana? ¿Cuál es el peso inicial de la persona B? ¿A qué peso llegó después de 16 semanas de dieta? ¿Cuántos kg perdió en estas 16 semanas? ¿Cuántos kg estuvo perdiendo por semana? ¿Por qué las rectas de A y B son paralelas? ¿Cuál es el peso inicial de la persona C? ¿A qué peso llegó después de 16 semanas de dieta? ¿Cuántos kg perdió en estas 16 semanas? ¿Cuántos kg estuvo perdiendo por semana? ¿Cuál es el peso inicial de la persona D? ¿A qué peso llegó después de 16 semanas de dieta? ¿Cuántos kg perdió en estas 16 semanas? ¿Cuántos kg estuvo perdiendo por semana? ¿Qué representa el punto donde la recta de D cruza la recta de C? ¿Qué peso tienen ambas personas cuando pasa esto? ¿Cuál de las dos personas pesa menos después de este tiempo: C o D? ¿Cuál recta tiene mayor inclinación: la de C o la de D? ¿Por qué? 54 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Completa la siguiente tabla. PERSONA Calorías PERDIDAS DIARIAMENTE REDUCCIÓN DE PESO (kg POR SEMANA) A B C 0.5 1 000 D Analiza la tabla y contesta la siguiente pregunta. Si una persona desea reducir su peso 2 kg por semana, ¿cuántas calorías debe perder diariamente? Recomiéndale un plan dietético y de ejercicio. Discute con todo tu grupo qué tan realistas son las ideas presentadas aquí. Propuesta Hidalgo 1er Grado BIOLOGÍA 55 La respiración como fenómeno cíclico (I) RespFenoCiclico01 En esta actividad analizaremos las gráficas del volumen pulmonar como función del tiempo durante el reposo y durante el ejercicio. Observa la gráfica siguiente, la cual muestra la variación con el tiempo del volumen en litros de los pulmones de una persona. Volumen pulmonar (I) 5 4.7 4.4 4.1 3.8 3.5 3.2 2.9 2.6 2.3 2 1.7 1.4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Tiempo (s) Notarás que la gráfica sube y baja repetidamente. El volumen de los pulmones aumenta al inhalar aire (entra a los pulmones) y disminuye cuando exhala aire (sale de ellos). Indica en la gráfica las secciones donde los pulmones se están llenando y donde se están vaciando. ¿Cuál es el volumen máximo al que llegan los pulmones en cada respiración? ¿Cuál es el volumen mínimo de los pulmones en cada respiración? ¿Se vacían completamente los pulmones en cada respiración? ¿Cuál es el volumen de aire que entra y sale en cada respiración? (Sugerencia: resta los dos valores anteriores.) 56 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Ahora observa el eje del tiempo y contesta: ¿cuántos segundos tarda cada respiración? (Sugerencia: una respiración completa va de máximo a máximo.) Nota en la gráfica que en 15 segundos hubo 5 respiraciones completas. De acuerdo con esto, ¿cuánto tiempo tarda cada respiración? (Compara ésta con tu respuesta anterior.) ¿Cuántas respiraciones tendrá la persona en un minuto? Escribe en una hoja qué piensas que suceda con este ciclo de la respiración cuando la persona esté exaltada o haciendo ejercicio. Ya vimos que, en cada respiración, esta persona inhala y exhala 0.6 litros de aire y que tiene 20 respiraciones por minuto. ¿Cuántos litros de aire inhala y exhala la persona en un minuto? El aire que entra a los pulmones contiene 20% de oxígeno. ¿Cuántos litros de oxígeno introduce la persona a su cuerpo por minuto? El aire que sale de los pulmones contiene sólo 15% de oxígeno. ¿Cuántos litros de oxígeno saca la persona de su cuerpo por minuto? ¿Cuánto oxígeno recibe su cuerpo por minuto? Esto equivale a 36 litros por hora. Propuesta Hidalgo 1er Grado BIOLOGÍA 57 La respiración como fenómeno cíclico (II) RespFenoCiclico02 Observa ahora la siguiente gráfica, la cual muestra la variación con el tiempo del volumen en litros de los pulmones de una persona inmediatamente después de haber corrido durante una hora. Indica en la gráfica una respiración, la parte donde los pulmones se están llenando y la parte donde se están vaciando. Volumen pulmonar (I) 5 4.7 4.4 4.1 3.8 3.5 3.2 2.9 2.6 2.3 2 1.7 1.4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Tiempo (s) ¿Cuál es el volumen máximo al que llegan los pulmones en cada respiración? ¿Cuál es el volumen mínimo de los pulmones en cada respiración? ¿Se vacían completamente los pulmones en cada respiración? ¿Cuál es el volumen de aire que entra y sale en cada respiración? ¿Cuántos segundos tarda cada respiración? Nota en la gráfica que en 10 segundos hubo 5 respiraciones completas. De acuerdo con esto, ¿cuánto tiempo tarda cada respiración? (Compara ésta con tu respuesta anterior.) ¿Cuántas respiraciones tendrá la persona en un minuto? 58 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria En el caso de una respiración más intensa, en cada respiración, esta persona inhala y exhala 3 litros de aire y tiene 30 respiraciones por minuto. ¿Cuántos litros de aire inhala y exhala la persona en un minuto? El aire que entra a los pulmones contiene 20% de oxígeno. ¿Cuántos litros de oxígeno introduce la persona a su cuerpo por minuto? El aire que sale de los pulmones contiene sólo 15% de oxígeno. ¿Cuántos litros de oxígeno saca la persona de su cuerpo por minuto? ¿Cuánto oxígeno recibe su cuerpo por minuto? Esto equivale a 270 litros por hora. Compara los valores obtenidos en reposo con los posteriores a un ejercicio intenso. Explica la razón de las diferencias y obtén algunas conclusiones. Propuesta Hidalgo 1er Grado BIOLOGÍA 59 Datos sobre enfermedades respiratorias (I) MortandadGral En esta actividad analizaremos uno de los componentes fundamentales de Sistema de Información en Salud, está conformado por las estadísticas de mortabilidad, no sólo porque éstas constituyen la piedra angular sobre la cual se inició, hace más de 100 años, la posibilidad de elaborar perfiles de salud de la sociedad en su conjunto, sino porque además se presenta, al interior de dicho sistema, la información más solida para la medición de las condiciones de salud de la población. Abre el archivo MortandadGral y analiza la información. Mortalidad general por sexo, según entidad federativa habitual. Estados Unidos Mexicanos, 1993 Entidad Federativa Defunciones Tasa * Hombres Mujeres N.E. Aguascalientes 3 474 4.4 1 919 1 555 0 Baja California 8 836 4.5 5 347 3 484 5 Baja California Sur 1 426 4.1 879 547 0 Campeche 2 279 3.9 1 360 918 1 Coahuila 9 463 4.4 5 417 4 032 14 Colima 2 251 4.8 1 294 955 2 Chiapas 15 359 4.4 8 634 6 718 7 Chihuahua 13 534 5.0 8 105 5 403 26 Distrito Federal 45 301 5.4 23 967 21 311 23 Durango Guanajuato Guerrero 5 664 3.9 3 440 2 222 2 20 789 4.8 11 444 9 296 49 9 563 3.4 5 907 3 654 2 Hidalgo 9 559 4.7 5 353 4 200 6 Jalisco 30 369 5.2 16 829 13 523 17 México 49 110 4.4 28 137 20 945 28 Michoacán 5 17 869 4.6 10 275 7 589 Morelos 6 390 4.8 3 709 2 674 7 Nayarit 3 920 4.4 2 432 1 484 4 11 Nuevo León 13 961 4.1 7 858 6 092 Oaxaca 19 023 5.9 10 667 8 349 7 Puebla 26 222 5.9 14 358 11 855 9 Querétaro 5 221 4.5 2 983 2 229 9 Quintana Roo 1 827 3.2 1 168 653 6 San Luis Potosí 9 937 4.6 5 566 4 358 13 Sinaloa 9 095 3.8 5 352 3 740 3 Sonora 9 609 4.9 5 691 3 916 2 Tabasco 6 737 4.2 3 939 2 792 6 10 10 803 4.4 6 359 4 434 Tlaxcala Tamaulipas 4 180 5.0 2 344 1 833 3 Veracruz 28 878 4.3 16 240 12 632 6 Yucatán 7 740 5.3 4 259 3 477 4 Zacatecas 5 861 4.3 3 275 2 569 17 416 335 4.7 235 961 180 068 306 Estados Unidos Mexicanos * 60 Tasa por 1 000 habitantes. Las defunciones no contienen corrección por subcobertura. Esto hace que las tasas del cuadro I no reflejen fielmente el nivel de la mortalidad de las Entidades Federativas. Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Datos sobre enfermedades respiratorias (II) InfecRespiratorias La información más relevante se presenta en el siguiente cuadro, en él se incluye información sobre causas seleccionadas, de interés relevante para la Secretaría de Salud (SSA): enfermedades diarreicas, enfermedades respiratorias agudas y sida. Al abrir el archivo InfecRespiratorias realiza la simulación de número de infectados y nota la importancia de la prevención en algunas infecciones particulares. Mortalidad por enfermedades infecciosas intestinales, infecciones respiratorias agudas y Síndrome de Inmunodeficiencia Adquirida, según entidad federativa habitual. Estados Unidos Mexicanos, 1993 Enfermedades infecciosas intestinales Entidad Federativa Defunciones Tasa Infecciones respiratorias agudas Defunciones Tasa SIDA Defunciones Tasa Aguascalientes 82 10.3 111 13.9 11 1.4 Baja California 112 5.8 334 17.2 109 5.6 Baja California Sur 26 7.4 54 15.4 6 1.7 Campeche 64 11.1 77 13.3 10 1.7 139 6.5 282 13.2 41 1.9 50 10.6 62 13.1 15 3.2 Coahuila Colima Chiapas 1 618 46.5 971 27.9 24 0.7 Chihuahua 155 5.7 514 18.9 50 1.8 Distrito Federal 664 7.9 2 233 26.4 804 9.5 73 5.1 177 12.3 14 1.0 Guanajuato 748 17.2 1 345 31.0 58 1.3 Guerrero 605 21.6 288 10.3 99 3.5 Hidalgo 241 11.8 570 27.9 35 1.7 Jalisco 478 8.2 1 386 23.9 350 6.0 1 859 16.7 3 980 35.8 514 4.6 Michoacán 414 10.7 542 14.1 63 1.6 Morelos 178 13.3 208 15.6 75 5.6 Nayarit 63 7.0 121 13.5 28 3.1 100 2.9 521 15.3 101 3.0 Oaxaca 1 741 53.7 1 012 31.2 39 1.2 Puebla 1 389 31.0 1 873 41.8 203 4.5 191 16.3 343 29.3 15 1.3 Durango México Nuevo León Querétaro Quintana Roo 43 7.4 65 11.2 22 3.8 San Luis Potosí 308 14.2 531 24.5 35 1.6 Sinaloa 129 5.4 223 9.4 43 1.8 Sonora 180 9.2 320 16.4 24 1.2 Tabasco 122 7.5 221 13.6 16 1.0 Tamaulipas 101 4.1 284 11.5 41 1.7 Tlaxcala 122 14.6 348 41.7 17 2.0 Veracruz 868 12.9 848 12.6 184 2.7 Yucatán 193 13.1 332 22.6 77 5.2 Zacatecas 143 10.4 288 21.0 15 1.1 13 207 14.9 20 496 23.2 3 164 3.6 Estados Unidos Mexicanos Tasa por 100 000 habitantes. Estimada en base a las proyecciones de población del Centro de Estudios en Población y Salud. Propuesta Hidalgo 1er Grado BIOLOGÍA 61 Escalas entre animales de diferentes tamaños (I) EscalaAnimales01 En esta actividad estudiaremos cómo cambian las proporciones de animales “similares en forma”, como un ratón, un gato, una vaca y un elefante. También analizaremos cómo varía el número de pulsaciones de su corazón. Observa los dos rectángulos siguientes. Uno es proporcional al otro ya que el largo del grande es tres veces mayor que el del chico y su ancho también es tres veces mayor. Mídelos para comprobarlo. ¿Has observado los troncos de los árboles? ¿Te parece que los árboles pequeños y los grandes están diseñados de manera proporcional como los rectángulos de arriba? En el espacio de abajo dibuja los troncos de dos árboles. Las líneas te dan su altura (una es dos veces mayor que la otra). Decide su ancho de acuerdo con tu experiencia. 62 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Piensas que animales similares (en forma) están diseñados por la naturaleza proporcionalmente como los rectángulos de arriba?, es decir, ¿sus dimensiones guardan la misma proporción? Supón que los seres humanos fuéramos dos veces más altos. ¿Piensas que la naturaleza nos hubiera diseñado exactamente iguales, con las mismas proporciones de altura y anchura? La respuesta a todas las preguntas anteriores es no. La naturaleza no puede construir animales o árboles grandes y pequeños con las mismas proporciones porque los más grandes se doblarían o se romperían. Para evitar esto, la naturaleza tiene que diseñar a los más grandes proporcionalmente “más gruesos”. Esto se ilustra en la figura siguiente, que podría pensarse como tres troncos diferentes o como tres huesos similares de animales diferentes (de un gato, de una vaca y de un elefante). Mide el largo y el ancho de cada uno y divide el largo entre el ancho para saber cuántas veces es más largo que ancho cada uno. ¿Son proporcionales estas figuras? ¿A qué conclusiones puedes llegar? Explica por qué piensas que las estructuras más grandes deben ser bastante más gruesas que las más pequeñas. Observa troncos de árboles grandes y pequeños para que distingas que los más grandes son más gruesos proporcionalmente. Propuesta Hidalgo 1er Grado BIOLOGÍA 63 Escalas entre animales de diferentes tamaños (II) EscalaAnimales02 La siguiente figura es un descubrimiento teórico de la relación que existe entre el número de pulsaciones por minuto del corazón de un animal y su masa en kilogramos. Pulsaciones por minuto 120 100 80 60 40 20 0 100 200 300 400 500 600 700 800 900 1000 Masa (kg) De acuerdo con esta gráfica, aproximadamente: ¿Cuántas pulsaciones por minuto tiene un hombre que pesa 80 kg? ¿Cuántas pulsaciones por minuto tendría un muchacho de 40 kg? ¿Cuántas pulsaciones por minuto tendría un niño de 20 kg? ¿Qué le pasa a esta cantidad de pulsaciones cuando decrece la masa de la persona? 64 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Tómate el pulso y pídele a tu profesor que se tome el suyo para que puedas comprobar lo anterior. ¿Cuántas pulsaciones predice la gráfica anterior que debe tener por minuto una vaca de 500 kg? ¿Cuántas pulsaciones predice la gráfica anterior que debe tener por minuto un animal de 1 000 kg? ¿Cuántas pulsaciones por minuto debe tener un elefante de 2 000 kg? (Sugerencia: estima este valor extrapolando visualmente la gráfica.) ¿Cuántas pulsaciones por minuto debe tener un gato de 5 kg? (Sugerencia: estima este valor extrapolando visualmente la gráfica.) ¿Qué puedes concluir a partir de los cuatro resultados anteriores? Las siguientes gráficas son continuación de la gráfica anterior por ambos lados (el izquierdo y el derecho), pero amplificadas. Pulsaciones por minuto 400 350 300 250 200 150 100 0 1 2 3 4 5 6 7 8 9 10 Masa (kg) Propuesta Hidalgo 1er Grado BIOLOGÍA 65 Pulsaciones por minuto 40 35 30 1000 1200 1400 1600 1800 2000 Masa (kg) De acuerdo con ellas, contesta de nuevo las siguientes preguntas y compara tus respuestas con las anteriores. ¿Cuántas pulsaciones por minuto debe tener un elefante de 2 000 kg? ¿Cuántas pulsaciones por minuto debe tener un gato de 5 kg? De acuerdo con las gráficas anteriores, contesta aproximadamente las siguientes preguntas: ¿Cuántas pulsaciones por minuto debe tener una rata de 1 kg? 2 ¿Cuántas pulsaciones por minuto debe tener un ratón de 50 g? ¿Qué le sucede a la cantidad de pulsaciones cuando el animal es cada vez más pequeño? De acuerdo con lo anterior, ¿podrán existir mamíferos con masas mucho más pequeñas que las del ratón? 66 Explica: Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Describe lo que aprendiste acerca de los cambios de escala entre seres vivos grandes y pequeños que coinciden más o menos en su forma. Propuesta Hidalgo 1er Grado BIOLOGÍA 67 Datos sobre las drogas y el ritmo cardiaco (I) DrogaCardio01 En esta actividad reflexionaremos que el uso de las Drogas no es un fenómeno nuevo; el conocimiento y el uso de estas, es probablemente, tan antiguo como el hombre mismo.- El hombre primitivo en busca de alimentos en praderas y bosques, descubrió ciertas plantas que parecían poseer misteriosos poderes, capaces de alterar su percepción o su estado de ánimo. Diversas drogas vegetales, que alteran la mente o el ánimo fueron identificadas e incorporadas a la estructura de la vida humana.- A pesar de la larga historia de las drogas, el uso de estas, actualmente se ha convertido en un problema de nuevas dimensiones y uno de los principales problemas en muchas partes del mundo; mismo que ha afectado a todo tipo de personas, sin distinción de sexo, raza, clase social, edad, profesión y ocupación. En 2005, los resultados de la Encuesta Domiciliaria sobre Abuso de Drogas en población general muestran una estabilización del consumo, pero alertan sobre un aumento de consumidores habituales. Datos recientes, en jóvenes de 14 a 18 años, de la Encuesta Estatal Escolar 2006, muestran una tendencia claramente descendente de consumo frente a años anteriores. Evolución del consumo de cannabis entre estudiantes 14 a 18 años (%). España. 1994 - 2006 45 40 35 30 25 20 15 10 5 0 1994 1996 Alguna vez en la vida 1998 2000 2002 Últimos 12 meses 2004 2006 Últimos 30 días Los chicos consumen con mayor frecuencia y con mayor intensidad que las chicas. Los propios jóvenes perciben consecuencias negativas del consumo de drogas: pérdidas de memoria, dificultades para trabajar o estudiar, tristeza, ganas de no hacer nada, y faltas a clase. 68 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Datos sobre las drogas y el ritmo cardiaco (II) DrogaCardio02 Abre el archivo DrogaCardio02 y analiza la simulación que se te presenta. Escribe tus conclusiones: En el cuadro siguiente se expresa el porcentaje de los encuestados en la Cd. de México que menciona cada tipo de droga. NOMBRES CONOCIDOS DE DROGAS DROGAS % ENTREVISTADOS Heroína 89.7 Cocaína 96.7 Cannabis 87.8 Anfetaminas 27.2 Alcohol 38.0 Tabaco 26.3 Alucinógenos 60.6 Drogas de diseño 59.5 Hipnosedantes 14.2 En la “Hoja2” analiza el efecto que te provocará si consumieras alguna de estas drogas. Propuesta Hidalgo 1er Grado BIOLOGÍA 69 Llena el siguiente cuadro de acuerdo a lo que observaste en la simulación: NOMBRES CONOCIDOS DE DROGAS Y ESPERANZA DE VIDA DROGAS EDAD Heroína Cocaína Cannabis Anfetaminas Alcohol Tabaco Alucinógenos Drogas de diseño Hipnosedantes Nota: Las drogas generalmente crean dependencia tanto física como psicológica y hacen vivir a quien las consume, en un mundo totalmente falso, en donde se sufre degradación física, mental, emocional y finalmente puede llegar a ocasionarle la muerte. 70 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Los experimentos de Mendel (I) ExperiMendel01 En la segunda parte explicaremos los resultados de algunos experimentos apoyándonos en un programa de cómputo basado en las leyes de la herencia de Mendel. Abre el archivo ExperiMendel01. Empecemos simulando un experimento en el que cruzamos plantas de chícharo de flor morada con plantas de chícharo de flor blanca (al aspecto externo se le denomina el fenotipo). En la actividad anterior usamos la letra F para designar la característica “color de la flor” (F representaba la flor morada y f la flor blanca). Escribe esta letra en la parte superior de la pantalla donde corresponde. A continuación hay que escoger los genotipos de la generación inicial. El genotipo de las plantas con flor morada puede ser FF, Ff o fF, ya que el color morado es dominante. Supongamos que las plantas de flor morada que cruzaremos son híbridas (Ff). ¿Cuál debe ser el genotipo de las plantas de flor blanca? Introduce en la parte superior de la pantalla estos dos genotipos de acuerdo con las opciones siguientes (el color rosa representa la parte femenina y el color azul la parte masculina). Opción 1: Ambas letras mayúsculas Opción 2: Mayúscula y minúscula Opción 3: Minúscula y mayúscula Opción 4: Ambas minúsculas Nota que los alelos femeninos son F y f y los alelos masculinos son ambos f. En la parte central de la pantalla se da una muestra de 60 genotipos de la siguiente generación, formados con un alelo femenino y otro masculino escogidos al azar. Cuenta cuántos genotipos resultaron de cada tipo y escribe tus resultados abajo: FF Ff fF ff Explica por qué los genotipos FF y fF no aparecen: En la parte inferior de la pantalla se puede simular un experimento escogiendo la cantidad de Propuesta Hidalgo 1er Grado BIOLOGÍA 71 fecundaciones que se quieren observar. Escoge 1 000 fecundaciones y observa las cantidades de cada genotipo que se obtienen. Escríbelas abajo: FF Ff fF ff De las 1 000 plantas representadas arriba, ¿cuántas tendrán flor morada? ¿Cuántas flor blanca? Más abajo en la pantalla encontrarás las cantidades de cada fenotipo. Comprueba con ellas tus resultados anteriores. Cada vez que oprimes la tecla F9 generas otras 1 000 fecundaciones. Observa la variación de los valores y escribe tus conclusiones. ¿Cuál es tu conclusión sobre el cruzamiento de plantas de chícharo de flor morada (Ff) con plantas de chícharo de flor blanca (ff)? Regresando a los experimentos de Mendel descritos en la actividad anterior: en el primero de ellos se cruzaron plantas de flor morada (variedad pura) con plantas de flor blanca. Los genotipos de la generación inicial deben ser entonces: FF y ff. Explica por qué estos genotipos corresponden al cruzamiento citado: Introduce en la parte superior de la pantalla estos dos genotipos de acuerdo con las opciones dadas anteriormente. 72 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria En la parte central de la pantalla se muestran 60 genotipos de la siguiente generación, formados con un alelo femenino y otro masculino escogidos al azar. ¿Por qué todos estos genotipos son de la forma Ff (híbridos)? En la parte inferior de la pantalla está simulado un experimento en el que hay 1 000 fecundaciones. ¿Qué resultado se obtiene sobre el fenotipo de las plantas (color de flor)? ¿Cuál es tu conclusión sobre el cruzamiento de plantas de flor morada (variedad pura) con plantas de flor blanca? Como vimos arriba, todas las plantas de la primera generación resultaron híbridas (Ff) con flor morada. En el segundo experimento las plantas de la primera generación se autofecundaron. Ahora los genotipos de esta nueva “generación inicial” deben ser Ff para ambos sexos. Escoge las opciones correspondientes en el programa (las opciones 2 y 3 son equivalentes ya que producen dos alelos diferentes en los gametos). De los 60 genotipos que corresponden a la segunda generación, mostrados en la pantalla, cuenta cuántos hay de cada tipo y escribe tus resultados abajo. FF Ff fF ff ¿Por qué hay de todos los tipos? (Sugerencia: ve los alelos en los gametos.) En la parte inferior de la pantalla escoge 1 000 fecundaciones y observa las cantidades que se obtienen de cada genotipo. Escríbelas abajo: FF Ff fF ff Propuesta Hidalgo 1er Grado BIOLOGÍA 73 Recordando el fenómeno de la dominancia de alelos, de las 1 000 plantas representadas antes, ¿cuántas tendrán flor morada? ¿Cuántas flor blanca? Con las cantidades de cada fenotipo dadas en el programa, comprueba tus resultados anteriores. Apretando cada vez la tecla F9, puedes simular otras 1 000 fecundaciones. Observa cómo varían los cuatro valores. ¿A qué conclusión puedes llegar? ¿Por qué los cuatro genotipos posibles tienen la misma probabilidad de que sucedan? ¿Qué puedes decir sobre la proporción de fenotipos, flor morada: flor blanca? ¿Cuál es tu conclusión sobre la autofecundación de plantas híbridas (Ff) de flor morada? Usa la tabla siguiente para explicar por qué en el experimento anterior, la probabilidad de cada uno de los genotipos (FF, Ff, fF y ff) es igual a ALELOS FEMENINOS ALELOS MASCULINOS 74 F f F FF Ff f fF ff Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Llena a continuación una tabla similar a la anterior para representar los otros dos experimentos discutidos al principio de esta actividad. Experimento 1: Cruzamiento de plantas híbridas de flor morada (Ff) con plantas de flor blanca (ff). ALELOS MASCULINOS ALELOS FEMENINOS f f F f De acuerdo con la tabla, ¿qué probabilidad tiene cada genotipo? Compara la generación inicial de este experimento con la generación siguiente. ¿Qué tienen de similar? Experimento 2: Cruzamiento de plantas de flor morada–variedad pura (FF) con plantas de flor blanca (ff). ALELOS MASCULINOS ALELOS FEMENINOS f f F F De acuerdo con la tabla, ¿qué probabilidad tiene cada genotipo? Propuesta Hidalgo 1er Grado BIOLOGÍA 75 Mendel realizó muchos otros experimentos con otras características de las plantas de chícharo: semillas lisas o rugosas, semillas amarillas o verdes, vainas verdes o amarillas, tallos largos o cortos (la primera característica mencionada es la dominante). Inventa un experimento como los presentados en esta actividad pero con una característica diferente. Descríbelo abajo y analízalo con el programa. Experimento: Resultados del experimento y conclusiones. 76 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Los experimentos de Mendel (II) ExperiMendel02 En la tercera parte continuaremos con los experimentos de Mendel, ampliando el estudio a dos características simultáneas. Abre el archivo ExperiMendel02. La “Hoja0”, ya utilizada en la parte anterior, muestra los resultados de experimentos de cruzamiento para una sola característica. La “Hoja1” está construida de manera similar pero presenta los resultados de dos características simultáneas. Escucha las indicaciones de tu profesor y realiza los experimentos que sugiera. Describe los resultados de tu exploración. Propuesta Hidalgo 1er Grado BIOLOGÍA 77 Distribución genética (I) DistriGenetica01 En esta actividad usaremos el programa de cómputo para observar cómo cambia la distribución genética de una población a lo largo de varias generaciones. Hagamos la siguiente pregunta: si tenemos una población con la mitad de pelo negro y la otra mitad de pelo rubio, ¿qué proporción de estos dos tipos esperaríamos tener en la generación siguiente? ¿Tú qué piensas? En la población anterior hay tres tipos de uniones: pelo negro–pelo negro; pelo negro– pelo rubio y pelo rubio–pelo rubio. ¿Crees tú que hay uniones más probables que otras? Si tu respuesta es sí, ¿cuáles son? Para que quede bien definido el problema tenemos que hacer dos suposiciones. La primera es que las tres uniones son igualmente probables, es decir, los individuos no tienen preferencia por uno u otro tipo. La segunda es que cada tipo de unión tiene igual cantidad de descendencia. Comenta sobre la segunda suposición, ¿es razonable? Comencemos con una situación muy simple, en la que tenemos toda una población con individuos de pelo negro y de raza pura para esta característica (homocigotos, con dos genes iguales). ¿Qué esperas encontrar en la siguiente generación? 78 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Abre el archivo DistriGenetica01. En él está simulada la situación anterior. Analiza la pantalla y contesta lo siguiente. En la generación de los hijos, ¿cuál es la distribución de genotipos? Pelo negro (homocigoto -PP) Híbrido (heterocigoto -Pp) Pelo rubio (homocigoto -pp) De acuerdo con esto, ¿qué proporción de individuos de pelo negro habrá en la generación de hijos? Estudiemos ahora una situación similar a la anterior, en la que tenemos toda una población con individuos de pelo negro, pero híbridos (heterocigotos con sus dos genes diferentes). ¿Por qué tienen estos individuos híbridos el pelo negro? Introduce en la celda correcta 1 000 de estos individuos (no se te olvide poner un cero en los individuos de pelo negro–homocigoto). En la generación de los hijos, ¿cuál es la distribución de genotipos? Pelo negro (homocigoto -PP) Híbrido (heterocigoto -Pp) Pelo rubio (homocigoto -pp) De acuerdo con esto, ¿qué proporción de individuos de pelo negro habrá en la generación de hijos? Explica cómo es posible que de una población de individuos de pelo negro se procree en la generación siguiente 25% de individuos con pelo rubio (sugerencia: la población inicial tiene genes Pp). Estudiemos ahora otra situación similar a las anteriores, en la que tenemos toda una población con individuos de pelo negro, pero la mitad de ellos son de raza pura (homocigotos) para esta característica y la otra mitad son híbridos (heterocigotos). Para esto, escribe en el programa las cantidades de los genotipos para los padres (500, 500 y 0). ¿Cuál es la distribución de genotipos para los hijos? Propuesta Hidalgo 1er Grado BIOLOGÍA 79 Pelo negro (homocigoto -PP) Híbrido (heterocigoto -Pp) Pelo rubio (homocigoto -pp) De acuerdo con esto, ¿qué proporción de individuos de pelo negro habrá en la generación de hijos? La pequeña proporción de individuos de pelo rubio, ¿de qué tipo de unión provienen? (Sugerencia: hay tres posibilidades: a) PP con PP; b) PP con Pp; c) Pp con Pp.) Regresando a la primera pregunta que hicimos en esta actividad (si tenemos una población con la mitad de pelo negro y la otra mitad de pelo rubio, ¿qué proporción de estos dos tipos esperaríamos tener en la generación siguiente?), veremos que realmente está mal planteada, ya que tenemos que decir qué genotipo tienen los individuos de pelo negro. Los dos siguientes ejemplos aclaran esto. Si tenemos una población con la mitad de pelo negro (homocigotos) y la otra mitad de pelo rubio, ¿qué porcentajes de cada genotipo se encontrarán en la generación siguiente? Pelo negro (homocigoto -PP) Híbrido (heterocigoto -Pp) Pelo rubio (homocigoto -pp) De acuerdo con esto, ¿qué proporción de individuos de pelo negro habrá en la generación de hijos? Ahora podemos preguntarnos qué se observará en la segunda generación, es decir, en los hijos de los hijos. Para obtener la respuesta, inserta en el programa los porcentajes de arriba como las cantidades de los genotipos para los padres (250, 500, 250). ¿Qué resultados obtuviste para los porcentajes de los genotipos de la segunda generación? Explica qué significan para ti los resultados anteriores: 80 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria ¿Qué pasará con las generaciones posteriores a ésta en lo que se refiere a su proporción de genotipos? Otra posibilidad parecida a la anterior es que tengamos al inicio una población con la mitad de pelo negro (heterocigotos) y la otra mitad de pelo rubio. Analiza esta población de manera similar a la anterior a lo largo de varias generaciones y escribe tus conclusiones. (Sugerencia: para la segunda generación usa las cantidades 625, 3 750 y 5 625 para los genotipos para representar exactamente los porcentajes obtenidos.) Propuesta Hidalgo 1er Grado BIOLOGÍA 81 Distribución genética (II) DistriGenetica02 En esta actividad continuaremos el estudio de los cambios en la distribución genética de una población a lo largo de varias generaciones. Abre el archivo DistriGenetica02. Este programa permite cambiar la población y la característica observada por medio de los nombres del “Carácter dominante” y del “Carácter recesivo” que están en la parte superior de la pantalla. Imaginemos una población de plantas con dos variedades de flores. Escribe en el programa “flor roja” debajo de la celda “Carácter dominante” y “flor blanca” debajo de la celda “Carácter recesivo”. Supongamos que tenemos 700 plantas de flor roja (homocigotos) y 300 plantas de flor blanca (homocigotos). ¿Qué porcentajes de cada genotipo se encontrarán en la generación siguiente? Flor roja (homocigoto -FF) Híbrido (heterocigoto -Ff) Flor blanca (homocigoto -ff) ¿Qué proporción de plantas tendrán flor roja? ¿Qué porcentajes de cada genotipo se encontrarán en la segunda generación? (Sugerencia: los hijos ahora pasan a ser padres, así que usa las cantidades 490, 420 y 90 para los genotipos de los “padres”.) Flor roja (homocigoto -FF) Híbrido (heterocigoto -Ff) Flor blanca (homocigoto -ff) ¿Qué proporción de plantas tendrán flor roja? ¿Qué porcentajes de cada genotipo se encontrarán en las generaciones subsecuentes? Supongamos ahora que tenemos otra proporción: 400 plantas de flor roja (homocigotos) y 600 plantas de flor blanca (homocigotos). ¿Qué proporción de plantas tendrán flor roja en la generación siguiente? 82 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Observarás que la proporción de flor roja aumentó con respecto a la proporción inicial. ¿Es cierto esto para el ejemplo anterior? ¿Es esto siempre cierto? (Sugerencia: varía como quieras las proporciones y observa las proporciones resultantes.) Regresemos a genética humana. En la actividad anterior usamos como ejemplo el color de pelo (negro, rubio) como característica. Escribe en el programa otra característica humana como color de ojos (negros, azules) u otra que tú conozcas que es dominante y recesiva. Con la característica que escogiste, diseña un experimento como los mostrados en esta actividad y en la anterior y analiza los resultados en varias generaciones. Experimento: Resultados: Conclusiones: En muchos casos no hay dominancia entre genes y su efecto en el aspecto externo es combinado dando una característica intermedia con respecto a la de los padres. Por ejemplo, hay flores rojas y blancas de una misma especie que al ser cruzadas generan flores rosas. En muchos animales que tienen su pelo claro y oscuro al ser cruzados se obtienen individuos con pelo de color intermedio. Discute las ideas del párrafo anterior con todo tu grupo. ¿Conoces alguna característica del ser humano que muestre el comportamiento descrito arriba de no dominancia? Propuesta Hidalgo 1er Grado BIOLOGÍA 83 ADN (ácido desoxirribonucleico) CadenaADN En esta actividad y la siguiente observaremos en el programa de cómputo algunas de las propiedades de la estructura del ácido desoxirribonucleico (ADN) y del ácido ribonucleico (ARN). Posiblemente tu profesor ya te habló de lo que son los ácidos nucleicos. A continuación daremos solamente un pequeño resumen de este tema. 1. Los ácidos nucleicos son enormes compuestos en forma de “hilos” de gran longitud con una estructura repetitiva. A las unidades que forman esta cadena se les conoce con el nombre de nucleótidos. El ácido nucleico es cadena de 2. Los nucleótidos están constituidos por un fosfato y un azúcar simple. 3. El azúcar de cada nucleótido tiene fija una estructura llamada base. El diagrama siguiente ilustra estas tres propiedades: fosfato azúcar fosfato base azúcar fosfato base azúcar fosfato base azúcar base Un ácido nucleico muy importante, en el que está guardada la información genética del individuo, es el ácido desoxirribonucleico. Este nombre lo obtiene del azúcar que contiene: la desoxirribosa. Para observar un modelo del ADN, abre el archivo CadenaADN. En él verás representada una parte pequeña de esta macromolécula. Nota que está formada por dos bandas (una arriba y otra abajo) de nucleótidos. Para que puedas observar mejor este modelo cambia el zoom de la pantalla de 50% a 100%. Las bases que contiene el ADN están representadas por letras. ¿Cuántas bases diferentes observas en la cadena? ¿Cuáles son las letras que las representan? , , y Existen cinco bases diferentes, con los nombres: citosina, uracilo, timina, adenina y guanina. De las letras que encontraste en el modelo, ¿cuáles cuatro bases aparecen en la molécula del ADN? , 84 , Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria , Como el ADN está formado por dos bandas, siempre una base de una banda tiene opuesta una base de la otra banda. Por ejemplo, en el primer nucleótido del modelo, la guanina (G) está opuesta a la citosina (C). Tu tarea ahora es explorar el modelo y deducir cuáles bases pueden estar opuestas a otras: ¿hay cierto patrón o están arregladas al azar? En las líneas siguientes explica lo que observaste. Vas a observar ahora cómo se duplica la molécula de ADN. Para esto, pasa a la segunda hoja de este archivo llamada “ADNcopy”. Observarás en rayos x, una parte de la molécula de ADN. Oprime una y otra vez, hasta 20 veces, la tecla F9, observando con cuidado lo que sucede cada vez. Escribe tus observaciones. Por último, sube la pantalla de la hoja de cálculo hasta que encuentres el modelo a colores de la autocopia de la molécula de ADN. Estúdialo y explica detalladamente esta duplicación. Propuesta Hidalgo 1er Grado BIOLOGÍA 85 ARN (ácido ribonucleico) CadenaARN En esta actividad observaremos en el programa de cómputo algunas de las propiedades de la estructura del ARN y su código genético para representar los aminoácidos. La molécula de ARN es otro ejemplo de ácido nucleico. Recordarás de la actividad anterior que los ácidos nucleicos son largas cadenas de unidades llamadas Los nucleótidos están constituidos por un fosfato y un simple. El azúcar de cada nucleótido tiene una estructura llamada El ARN difiere del ADN en tres propiedades básicas. Dos de ellas las mencionaremos a continuación. La tercera la tendrás que descubrir. 1. El ARN está formado por una sola banda. El ADN por bandas. 2. El azúcar del ARN es la ribosa. El azúcar del ADN es la Para obtener la tercera diferencia, abre el archivo CadenaARN. En él veras representada una parte pequeña de esta macromolécula. Amplifícala al 100% con el zoom de la hoja de cálculo y contesta la siguiente pregunta. 3. Las cuatro bases que aparecen en la molécula de ARN son: , , , Las cuatro bases que aparecen en la molécula de ADN son: citosina (C), timina (T), adenina (A) y guanina (G). Posiblemente tu profesor ya te habló del proceso de síntesis de proteínas. Aquí sólo daremos una descripción muy breve. La información genética almacenada en la cadena del ADN se transcribe a una molécula intermediaria, el ARN-mensajero. En la cadena de las bases, éste tiene codificada la secuencia de aminoácidos de las proteínas que serán construidas. Como observarás en la pantalla, cada tres bases de la cadena del ARN representa un aminoácido. Por ejemplo, el triplete G-U-A representa el aminoácido “Valina”. Tu tarea, por medio del programa, es descubrir la correspondencia de tripletes y aminoácidos. Para esto, cada vez que oprimas la tecla F9 cambiará la secuencia de bases. 86 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Hay 64 tripletes diferentes. Encuentra los más que puedas y, en la lista que sigue, asóciales su aminoácido correspondiente (nota que varios tripletes pueden tener el mismo aminoácido codificado, ya que sólo existen 20 aminoácidos). TRIPLETE AMINOÁCIDO TRIPLETE UUU Fenillanina UCU UAU UGU UUC UCC UAC UGC UUA UCA UAA UGA UUG UCG UAG UGG CUU CCU CAU CGU CUC CCC CAC CGC CUA CCA CAA CGA CUG CCG CAG CGG AUU ACU AAU AGU AUC ACC AAC AGC AUA ACA AAA AGA AUG ACG AAG AGG GUU GCU GAU GGU GUC GCC GAC GGC GCA GAA GGA GCG GAG GGG GUA GUG Valina AMINOÁCIDO TRIPLETE AMINOÁCIDO TRIPLETE AMINOÁCIDO Una proteína tiene la siguiente secuencia de aminoácidos: iniciación de cadena cisteína glutamato serina isoleucina alanina tirosina histidina prolina valina serina glicina treonina lisina glutamina leucina metionina arginina terminación de cadena ¿Cómo debe venir codificada la secuencia de bases del RNA para que se sintetice esta proteína? Compara tu secuencia con las de otros equipos. ¿Qué encontraste? Propuesta Hidalgo 1er Grado BIOLOGÍA 87 Distribución de edades en poblaciones DistribEdadPob En esta actividad usaremos el programa de cómputo para estudiar la distribución de edades de una población, variando las tasas de natalidad y mortalidad de los diferentes grupos. Abre el archivo DistribEdadPob. En él verás representada una población seccionada en 10 grupos de edades distintas: de 0 a 10 años, de 10 a 20 años, etcétera. Cada uno de estos grupos tiene asociada una “Cantidad inicial” de individuos en ese grupo (de 1 000 al inicio del programa, pero pueden ser cambiadas). Los grupos de edades 20-30, 30-40 y 40-50 tienen también designados una “Fecundidad” (0.6, 0.5, 0.3, respectivamente). Estos valores representan la proporción de hijos que tendrá cada uno de estos grupos. Por ejemplo, en el grupo de 20 a 30 años, por tener una fecundidad de 0.6, por cada 1 000 individuos de este grupo nacerán 600 bebés por año (éste es un valor alto para una población humana, pero después lo podemos cambiar). Se supone que los otros siete grupos tienen una fecundidad de cero, ya que son demasiado jóvenes o demasiado viejos para tener bebés. ¿Por qué crees que los grupos de 30 a 40 y de 40 a 50 tienen asignadas fecundidades menores que la del grupo de 20 a 30 años? Por último, a cada grupo se le asocia una “Tasa de mortalidad” (el programa viene con un valor de 0.1 para todos). Esta tasa representa la fracción de individuos que muere dentro del grupo cada año. Por ejemplo, el valor de 0.1 significa que 10% de los individuos de ese grupo morirán cada año (también este valor es alto pero puede modificarse después). 88 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria En la parte superior está el tiempo en años con un control que lo hace avanzar o retroceder. Presiona este control y observa cómo se mueve la gráfica de barras correspondiente. En el espacio siguiente copia esta gráfica para el tiempo 20 (años). ¿Cuántos niños de 0 a 10 años hay en este tiempo? (Son más de la mitad de la población total.) Nota que los niños y jóvenes de entre 0 y 20 años representan más de las tres cuartas partes de la población. ¿Qué puedes concluir acerca de esto? Cambia todas las tasas de mortalidad a cero y observa nuevamente el tiempo 20. ¿Qué diferencias observas en los valores de cada grupo de la población y su total? ¿Qué diferencias observas en la forma de la gráfica? Cambia ahora la tasa de mortalidad del grupo 0-10 al valor 1, es decir, todos los bebés mueren en su primer año (deja las otras tasas de mortalidad en cero). Observa cómo varía la distribución de individuos de diferentes edades con el paso del tiempo. Propuesta Hidalgo 1er Grado BIOLOGÍA 89 En el espacio siguiente copia a la izquierda la gráfica de barras correspondiente al tiempo 20 y a la derecha la gráfica correspondiente al tiempo 50. Compara la forma de estas gráficas con la de la página anterior y describe las diferencias: ¿Por qué si la tasa de mortalidad del grupo 0-10 es de 1, este grupo no desaparece? ¿Qué le sucederá a esta población al transcurrir mucho tiempo? Discute con tus compañeros si ésta es una situación realista que se puede encontrar en algún país y escribe tus conclusiones. Cambia ahora la tasa de mortalidad del grupo 20-30 al valor 1, con todas las otras tasas de mortalidad en cero. Observa cómo varía la distribución de individuos de diferentes edades con el tiempo. 90 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria En el espacio siguiente copia a la izquierda la gráfica de barras correspondiente al tiempo 20 y a la derecha la gráfica correspondiente al tiempo 100. Escribe tus conclusiones. Explora varias situaciones diferentes cambiando los valores de las tasas y describe abajo qué tipos de gráficas encontraste y su significado. Propuesta Hidalgo 1er Grado BIOLOGÍA 91 Epidemias Epidemia En esta actividad usaremos el programa de cómputo para estudiar cómo y cuándo una epidemia se esparce en una población. En una epidemia hay dos tipos principales de individuos: Infectados: (representados en el programa con la letra I) son los individuos que han adquirido la enfermedad y están enfermos actualmente. Susceptibles: (representados en el programa con la letra S) son los individuos que están sanos pero pueden contraer la enfermedad por “contacto” con un infectado. Abre el archivo Epidemia. Observarás en la pantalla cinco propiedades de una epidemia, las cuales pueden variarse. Éstas aparecen en la siguiente lista. NIVEL DE INFECCIÓN 1 (1, 2, 3, 4,...) Porcentaje de infectados que diariamente Se recuperan pero vuelven a ser susceptibles 20% Se recuperan y pasan a ser inmunes 0% Mueren 0% Siguen infectados 80% Estas propiedades se explicarán poco a poco. El “nivel de infección” representa qué tan fácil es contagiarse. Un 1 representa poco probable, y números mayores significan mayor posibilidad de contagio. Una vez infectado, un individuo tiene cuatro posibilidades, las cuales están señaladas en la lista de arriba. Por lo pronto consideraremos sólo dos: 1. El individuo se recupera de la enfermedad, pero eventualmente puede contagiarse otra vez, es decir, vuelve a ser susceptible. En el cuadro de arriba hemos asignado un 20% a esta posibilidad. 2. El individuo sigue infectado. Como elegimos arriba que un 20% de los individuos infectados se recuperarán diariamente, el 80% seguirá infectado. Corramos ahora el programa con estos valores para observar cómo funciona. Para esto, haz “clic” en el botón azul, “Paso al cuadro de estados iniciales”. 92 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Observarás 280 casillas, la mayoría con una S (representando a los individuos susceptibles) y las cuatro centrales con una I (representando a los ya infectados). Este cuadro muestra el estado inicial de tu población (t = 0). Para comenzar la simulación, haz “clic” en el botón azul “Iniciar”. Observarás casi la misma pantalla pero con el valor del tiempo t = 1, y con los conteos del número de susceptibles y de infectados. Para continuar la simulación y avanzar el tiempo, oprime la tecla F9 una y otra vez. Describe lo que observaste. Para realizar otra simulación, haz “clic” en el botón azul, “Empezar de nuevo”. Espera un momento y el programa te regresará a la pantalla inicial de propiedades. Cambia el nivel de infección de 1 a 4 y repite los pasos anteriores para que observes de nuevo el progreso de la simulación con este valor, presionando la tecla F9. Describe lo que observaste. Escoge una casilla cualquiera que representa un individuo particular de la población. Oprime muchas veces la tecla F9 y observa el estado de este individuo conforme pasa el tiempo. ¿Qué puedes decir de esto? ¿Qué le pasa al grupo de infectados y al grupo de susceptibles después de mucho tiempo? Propuesta Hidalgo 1er Grado BIOLOGÍA 93 ¿Se acabará alguna vez la epidemia de esta enfermedad? Explica por qué: Empieza de nuevo otra simulación. Otro posible curso de una enfermedad en un individuo es el siguiente: El individuo, después de estar infectado, queda inmune. Así, podemos tener otro tipo de individuo en la población: Inmunes: (representados en el programa con la letra n) son los individuos que se han recuperado de la enfermedad y ya no pueden contraer la otra vez. Para observar el efecto que tiene esta inmunidad, cambia de 20 a 0 el porcentaje de individuos que al recuperarse vuelven a ser susceptibles, y cambia de 0 a 20 el porcentaje de individuos que al recuperarse se vuelven inmunes. Deja todo lo demás igual y corre como antes la simulación respectiva. Explica a continuación lo que observas. Oprime ahora la tecla F9 muchas veces hasta que la epidemia termine. ¿Cuántos susceptibles, infectados e inmunes quedaron? ¿Qué significa esto? Repite la simulación anterior, pero con un nivel de infección de 2. Explica a continuación lo que observas. Oprime ahora la tecla F9 muchas veces hasta que termine la epidemia. ¿Cuántos susceptibles, infectados e inmunes quedaron? 94 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Compara esto con el caso anterior y anota tus conclusiones. Empieza otra simulación. Regresa el valor del nivel de infección a 4. Para combinar los dos casos anteriores, asigna a los porcentajes de individuos que “se recuperan pero vuelven a ser susceptibles” y los que “se recuperan y pasan a ser inmunes” un valor de 10. Corre la simulación observando detenidamente lo que pasa. Escribe tus observaciones. Empieza de nuevo otra simulación. Otro posible curso de una enfermedad en un individuo es el siguiente: El individuo muere a causa de la infección. Así, podemos tener: Muertos: (representados en el programa con el símbolo _ ). Para observar el efecto de una enfermedad que puede matar a los individuos, cambia el porcentaje de individuos que “se mueren” a 10. Deja todo lo demás igual. Antes de pasar al cuadro de estados iniciales, presiona la tecla F9 para que el programa calcule el porcentaje de los individuos que “siguen infectados” (100% 10% 10% 10% 70%). Corre como anteriormente la simulación respectiva. Explica a continuación lo que observas. Repite la simulación anterior pero con un nivel de infección de 2. Explica a continuación lo que observas. Propuesta Hidalgo 1er Grado BIOLOGÍA 95 Compara los resultados con los del caso anterior: Corre una simulación diseñada por ti. Escoge los porcentajes que quieras (no te olvides de oprimir la tecla F9 para el cálculo de los que “siguen infectados”). Varía el nivel de infección desde 1 hasta 4 y observa cada uno de los resultados. Describe cada uno y explica las diferencias entre ellos. Presenta tu caso a todo el grupo. 96 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Competencia entre dos especies CompEspecies En esta actividad usaremos el programa de cómputo para estudiar la competencia entre dos especies que comparten una misma región. Abre el archivo CompEspecies. A la derecha de la pantalla observarás las propiedades de ambas especies: ESPECIE A ESPECIE B Cantidad inicial 100 100 Tasa de natalidad 0.06 0.05 Capacidad de la región 5 000 3 000 0 0 Efectividad Aunque probablemente ya tienes una idea del significado de estas cantidades, después las explicaremos con mayor detalle. A la izquierda de la pantalla puedes observar las gráficas correspondientes del comportamiento de ambas especies con el tiempo. Describe cada una de estas gráficas (antes de hacer esto, platica con tus compañeros y otros equipos sobre su significado). Gráfica de la especie A: Gráfica de la especie B: ¿Por qué la gráfica de la especie A sube más alto que la de la especie B? (Sugerencia: observa los valores de la capacidad de la región para cada especie mostrados arriba. Esta propiedad representa la máxima cantidad de individuos sostenible por la región.) Propuesta Hidalgo 1er Grado BIOLOGÍA 97 ¿Por qué la gráfica de la especie A sube más rápidamente que la de la especie B? (Sugerencia: observa los valores de la tasa de natalidad de cada especie dados antes.) Variaremos a continuación una a una las primeras tres propiedades de las dos especies: “Cantidad inicial”, “Tasa de natalidad” y “Capacidad de la región”, para entender mejor su significado. Para esto, usa el control asociado a cada una de ellas cuando se te pida. Aumenta y disminuye la cantidad inicial de individuos de la especie A. Observa cómo la gráfica correspondiente a esta especie inicia en el eje y de acuerdo con estos valores (cuando termines regresa esta cantidad a su valor original de 100). Escribe qué representa esta cantidad inicial. Aumenta y disminuye la cantidad inicial de individuos de la especie B. Cuando este valor llega a 1 000, ¿de qué valor sale la gráfica correspondiente a esta especie en el eje y? (Cuando termines regresa esta cantidad a su valor original de 100.) Escribe qué representa esta cantidad inicial. Aumenta y disminuye la tasa de natalidad de la especie A. Describe abajo lo que sucede con la gráfica de esta especie y explícalo en función de que estás variando su tasa de natalidad (cuando termines, regresa el valor de esta tasa a 0.06, que representa un crecimiento de 6%). Aumenta y disminuye la tasa de natalidad de la especie B. Describe abajo lo que sucede con la gráfica de esta especie y explícalo en función de que estás variando su tasa de natalidad (cuando termines, regresa el valor de esta tasa a 0.05, que representa un crecimiento de 5%). 98 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Aumenta y disminuye la capacidad de la región para la especie A. Describe abajo lo que sucede con la gráfica de esta especie y explícalo en función de que estás variando la capacidad máxima de la región para esta especie (cuando termines, regresa el valor de esta capacidad a 5 000 individuos). Aumenta y disminuye la capacidad de la región para la especie B. Describe abajo lo que sucede con la gráfica de esta especie y explícalo en función de que estás variando la capacidad máxima de la región para esta especie (cuando termines, regresa el valor de esta capacidad a 3 000 individuos). Explica por qué piensas que la capacidad de ambas especies es diferente aun cuando están compartiendo la misma región. Es muy importante notar que, a medida que pasa el tiempo, las poblaciones se estabilizan en su propio valor de la capacidad de la región (la gráfica permanecerá horizontal, sin subir ni bajar). Ahora pasemos a la propiedad que representa la interacción entre las dos especies: su efectividad. Aumenta la efectividad de la especie A. Describe abajo lo que sucede con la gráfica de la especie B y explícalo en función de que la especie A tiene mayor efectividad ya sea para obtener su alimento (quitándole alimento a la especie B) o para combatir con la especie B (cuando termines, regresa el valor de esta efectividad a 0). Propuesta Hidalgo 1er Grado BIOLOGÍA 99 Nota que, para efectividades pequeñas de la especie A, la especie B sólo reduce su valor de estabilidad, pero con mayores efectividades de la especie A, la especie B desaparece. Aumenta la efectividad de la especie B. Describe abajo lo que sucede con la gráfica de la especie A y explícalo en función de que la especie B tiene mayor efectividad, ya sea para obtener su alimento (quitándole alimento a la especie A) o para combatir con la especie A (cuando termines, regresa el valor de esta efectividad a 0). En las investigaciones anteriores, cambiamos las propiedades de las dos especies una por una. Ahora podemos averiguar el efecto de un cambio simultáneo de dos propiedades (aquí nos concentraremos en las efectividades que son las propiedades más importantes de esta interacción). Por ejemplo, puedes dejar ahora la efectividad de la especie A en 1 y aumentar la efectividad de la especie B. Escribe tus observaciones al hacer esto. Cambia ahora las seis propiedades a tu gusto y escoge una situación que te parezca interesante. Escribe abajo los valores de las propiedades que elegiste, copia las gráficas que obtuviste y explica lo que está sucediendo con las dos especies (en particular, decide cuál de las dos “gana” a la otra y por qué). Presenta la situación anterior a todo tu grupo. 100 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Interacción depredador-presa DepredadorPresa En esta actividad usaremos el programa de cómputo para estudiar la interacción entre dos poblaciones conocida como depredador-presa. Un ejemplo de este tipo de interacción es la relación entre una población de zorras (depredador) y una población de conejos (presa). Abre el archivo DepredadorPresa. En la parte derecha de la pantalla observarás las propiedades de ambas poblaciones. En la parte superior tenemos las del depredador: Cantidad inicial 800 Tasa de mortandad 0.1 Efectividad de caza 1 En la parte inferior tenemos las propiedades de la presa: Cantidad inicial 800 Tasa de crecimiento 0.1 Alimento disponible 4 000 A la izquierda de la pantalla puedes observar las gráficas del depredador y la presa como función del tiempo. Describe cada una de estas gráficas (antes de hacer esto, platica con tus compañeros y otros equipos sobre su significado). Gráfica del depredador: Gráfica de la presa: Para entender cada una de las propiedades anteriores, a continuación variaremos una por una. Para esto, usa el control asociado a cada una de ellas. Aumenta la cantidad inicial de individuos del depredador de 800 a 1 600. Observa cómo la gráfica correspondiente del depredador inicia en el eje y de acuerdo con estos valores. Propuesta Hidalgo 1er Grado BIOLOGÍA 101 Disminuye esta cantidad a 400 y vuélvela a aumentar al valor de 800. Escribe tus impresiones. Aumenta la tasa de mortandad del depredador. Nota que esto produce que la parte inicial de la gráfica del depredador descienda más y más, representando más muertes. ¿Desaparece completamente el depredador con tasas más altas de mortalidad? Describe lo que pasa (regresa el valor de esta tasa a 0.1 cuando termines). Varía la efectividad de caza del depredador. Primero redúcela a cero y observa lo que sucede con las gráficas. Aumenta el valor a 0.5 (no muy buen cazador) y observa la amplitud de las oscilaciones. Escribe todas tus observaciones (regresa el valor de esta efectividad a 1 cuando termines). Aumenta ahora la cantidad inicial de individuos de la presa de 800 a 1 600. Observa cómo la gráfica correspondiente de la presa inicia en el eje y de acuerdo con estos valores. Disminuye esta cantidad a 400 y vuélvela a aumentar al valor de 800. Escribe tus impresiones. Decrece la tasa de crecimiento de la presa a cero. Observa lo que les pasa a las gráficas y coméntalo. Aumenta esta tasa y observa el efecto. Describe abajo lo que sucede (regresa el valor de esta tasa a 0.1 cuando termines). Varía el alimento disponible para la presa. Primero auméntalo y después redúcelo. Describe abajo todas tus observaciones (regresa este valor a 4 000 cuando termines). 102 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Fibonacci y sus conejos FibonacciConejos En esta actividad utilizaremos una hoja de cálculo para representar modelos matemáticos del crecimiento de poblaciones que toman en cuenta diferentes grupos de edades. Construye una hoja de cálculo como la que aparece en la tabla siguiente. En las celdas A6, B6, C6, D6 y E5 debes escribir las fórmulas apropiadas que calculen esos valores, de acuerdo con el modelo presentado en la actividad anterior (por ejemplo, B6 = $B$2*C5 y C6 = C5+B5). Al terminar, copia estas fórmulas hacia abajo. A1 A B 1 Fecundidad 2 1 C D E 3 4 Tiempo (meses) Núm. de parejas de bebés Núm. de parejas de adultos Número total de parejas Razón de adultos-bebés 5 1 1 0 1 0 6 2 0 1 1 #¡DIV/0! 7 3 1 1 2 1 8 4 1 2 3 2 9 5 2 3 5 1.5 Comprueba ahora los resultados encontrados de la actividad anterior, tomando en cuenta los siguientes pasos. • Para el caso de la tabla anterior encuentra hacia qué valor tiende la razón de adultos a bebés: • Cambia los valores iniciales de bebés y adultos a 100 y 2 000 y a otros valores para observar si se mantiene la razón áurea: • Cambia el valor de la fecundidad a 6 y observa hacia qué valor tiende ahora la razón de adultos a bebés: ¿Qué significa esta razón? Propuesta Hidalgo 1er Grado BIOLOGÍA 103 • Encuentra el valor de la fecundidad que hace estabilizarse a la razón entre adultos y bebés en 1: ¿Qué significa esta razón? • Encuentra el valor de la fecundidad que hace estabilizarse a la razón entre adultos y bebés en 1: ¿Qué significa esta razón? • Para alguno de los dos últimos casos, traza las gráficas del número de bebés, del número de adultos y del total como función del tiempo. En el espacio de abajo, copia estas gráficas y describe el tipo de crecimiento que observas. Guarda tu hoja de cálculo para que la puedas utilizar en una actividad posterior. 104 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Temperatura corporal TempCorporal En esta actividad analizaremos las gráficas de la temperatura corporal de animales en relación con la temperatura del medio ambiente. Observa la figura siguiente, la cual muestra la temperatura del cuerpo de una persona y de una lagartija al variar la temperatura del medio ambiente (oC representa grados centígrados). De acuerdo con las gráficas, contesta lo siguiente: Temperatura corporal (oC) 40 Humano 30 20 Lagartija 10 0 0 10 20 30 40 o Temperatura del medio ambiente ( C) ¿Cuál es la temperatura de la lagartija cuando la temperatura ambiente es de 20 oC? ¿Cuál es la temperatura de la lagartija cuando la temperatura ambiente es de 40 oC? ¿Cuál es la temperatura de la lagartija cuando la temperatura ambiente es de 5 oC? Partiendo de estos resultados, ¿a qué conclusión puedes llegar? ¿Cuál es la temperatura de la persona cuando la temperatura ambiente es de 20 oC? ¿Cuál es la temperatura de la persona cuando la temperatura ambiente es de 40 oC? ¿Cuál es la temperatura de la persona cuando la temperatura ambiente es de 5 oC? Propuesta Hidalgo 1er Grado BIOLOGÍA 105 Partiendo de estos resultados, ¿a qué conclusión puedes llegar? La temperatura corporal de animales como reptiles, anfibios y peces cambia con la del medio ambiente. La lagartija es un ejemplo. En un medio ambiente frío, ¿cómo esperas que sean los movimientos de este tipo de animales: rápidos o lentos? ¿Por qué? En un medio ambiente muy caluroso bajo el sol, el cuerpo de estos animales puede calentarse demasiado. ¿Qué crees que hagan estos animales para evitarlo? Por el contrario, la temperatura del cuerpo de animales como las aves y los mamíferos se mantiene más o menos constante. El ser humano es un ejemplo. ¿Cómo crees que mantiene el cuerpo de estos animales una temperatura constante? (Sugerencia: piensa en lo que haces cuando se siente mucho frío o mucho calor.) ¿Por qué crees que es importante mantener la temperatura del cuerpo a una temperatura “óptima” constante? (Sugerencia: piensa en el funcionamiento de las células del cuerpo y su efecto en los órganos.) Discute las ideas anteriores con todo tu grupo. ¿Piensas que la temperatura de todas las aves y mamíferos se mantiene a 37o C como la de una persona? Averígualo (le puedes preguntar a un veterinario cuál es la temperatura normal de perros, gatos, etcétera). 106 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Tipos sanguíneos (I) TipoSanguineo01 En esta actividad usaremos el programa de cómputo para estudiar las proporciones de los grupos sanguíneos en una población. Como posiblemente sepas, existen cuatro tipos (fenotipos) sanguíneos: O, A, B y AB. Supón que vas a una población y tomas muestras de sangre de 100 personas. ¿Cuántas personas habrá de cada tipo? Abre el archivo TipoSanguineo01 para obtener la respuesta. En la tabla siguiente escribe las cantidades dadas por el programa. CANTIDADES EN CADA TIPO O A ¿Cuál fue el tipo más frecuente? B AB ¿Cuál fue el tipo menos frecuente? Si oprimes la tecla F9 el programa te dará otra muestra de 100 personas. En la siguiente tabla escribe las nuevas cantidades dadas por el programa. CANTIDADES EN CADA TIPO O ¿Cuál fue el tipo más frecuente? A B AB ¿Cuál fue el tipo menos frecuente? ¿Por qué son diferentes las cantidades de la primera y la segunda tabla? ¿Difieren mucho las cantidades de la primera y la segunda tabla? ¿Por qué? Propuesta Hidalgo 1er Grado BIOLOGÍA 107 Toma ahora muestras de una persona a la vez (para esto escribe 1 en la celda “Cantidad en la muestra”). Presionando la tecla F9, el programa te dará cada vez una persona diferente. Escribe abajo la lista de los tipos que vayan apareciendo en la pantalla: O, A, B o AB. (Nota que si no observas cambios en la pantalla al oprimir la tecla F9 es porque el tipo se repitió y tienes que escribirlo de nuevo en la lista.) Examina estas 60 muestras. ¿Cuál tipo resultó ser el más frecuente? ¿Cuál tipo resultó ser el menos frecuente? Ahora quieres encontrar la siguiente persona con tipo de sangre AB. Cuenta las veces que necesitas oprimir la tecla F9 para que aparezca el tipo AB: Compara este valor con el de otros equipos. Cambia ahora la “Cantidad en la muestra” a 1 000. Oprimiendo la tecla F9, el programa te dará cada vez muestras de 1 000 personas. Llena la siguiente tabla con las cantidades dadas por el programa a 10 grupos de 1 000 personas. CANTIDADES EN CADA TIPO O 108 A B Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria AB Observa las cantidades de cada tipo y contesta las siguientes preguntas. ¿Alrededor de qué valor oscilan las cantidades del tipo O? ¿Alrededor de qué valor oscilan las cantidades del tipo A? ¿Alrededor de qué valor oscilan las cantidades del tipo B? ¿Alrededor de qué valor oscilan las cantidades del tipo AB? Sobre la base de las cantidades anteriores y recordando que hay 1 000 personas por muestra, responde: Aproximadamente, ¿qué porcentaje de la población tiene el tipo O? Aproximadamente, ¿qué porcentaje de la población tiene el tipo A? Aproximadamente, ¿qué porcentaje de la población tiene el tipo B? Aproximadamente, ¿qué porcentaje de la población tiene el tipo AB? Tarea El programa que usaste es sólo un ejemplo de las frecuencias posibles que puede tener una población en sus grupos sanguíneos. En él se simulaba una población con 50% del tipo O, 35% del tipo A, 10% del tipo B y 5% del tipo AB, lo cual es representativo de muchos lugares del mundo (compara estos porcentajes con los que obtuviste en la primera parte de esta actividad). Sin embargo, la proporción de grupos sanguíneos varía de acuerdo con la región del planeta. Por ejemplo, en Australia es muy frecuente el tipo A sanguíneo y en Asia es muy frecuente el tipo B. En la siguiente tabla se dan algunos ejemplos de poblaciones y sus distribuciones sanguíneas. POBLACIÓN 0 A B AB Negros estadounidenses 47% 28% 20% 5% Ingleses 47% 42% 8% 3% Indígenas de Perú 100% 0% 0% 0% Pigmeos africanos 31% 30% 29% 10% Aborígenes australianos 34% 66% 0% 0% Tuamotus de Polinesia 48% 52% 0% 0% ¿Qué grupo sanguíneo es, en general, el más frecuente? ¿Qué grupo sanguíneo es el más frecuente para los aborígenes australianos? Propuesta Hidalgo 1er Grado BIOLOGÍA 109 ¿Qué grupo sanguíneo es, en general, el menos frecuente? ¿Cuál es la probabilidad de encontrar entre los indígenas del Perú un individuo con sangre tipo O? ¿Cuál es la probabilidad de que un inglés tenga sangre tipo A? Estudia los valores de la tabla anterior y coméntalos con tus compañeros de equipo. Escribe aquí algunas de tus conclusiones. Tarea Al trasplantar órganos, el individuo receptor tiene, por lo general, una reacción al tejido extraño en su cuerpo y tiende a rechazarlo. También en transfusiones de sangre se presentan este tipo de reacciones. La tabla siguiente muestra en qué casos habrá una reacción cuando una persona (donador) cede sangre a otra (receptor). RECEPTOR O A B AB DONADOR O A Reacción Reacción B Reacción Reacción AB Reacción Reacción Reacción Partiendo de la tabla anterior explica por qué a las personas de tipo O se les llama “donadores universales”: Igualmente explica por qué a las personas de tipo AB se les llama “receptores universales”: De acuerdo con la información anterior, llena la siguiente tabla (observa el ejemplo). GRUPO PUEDE DONAR A: PUEDE RECIBIR DE: O O, A, B y AB O A B AB 110 Enseñanza de las Ciencias a través de Modelos Matemáticos para la Educación Secundaria Tipos sanguíneos (II) TipoSanguineo02 En esta actividad usaremos el programa de cómputo para estudiar las proporciones del llamado factor Rh en una población. En 1939 se descubrió una incompatibilidad sanguínea entre individuos del mismo tipo sanguíneo (O, A, B o AB). Se encontró que ésta se debía a otro elemento en la sangre que poseían algunas personas (Rh positivo) y otras no (Rh negativo). Tu tarea en esta actividad es determinar la proporción de personas que son Rh positivas en una población. Para esto, abre el archivo TipoSanguineo02 y pasa a su “Hoja2” llamada “Con Rh”. En ella se han tomado muestras de sangre de 100 personas y se han clasificado de acuerdo con su tipo sanguíneo y su factor Rh. TIPO DE SANGRE CANTIDAD TOTAL CANTIDAD RH+ CANTIDAD RH- O A B AB ¿De cuáles hay más: Rh+ o Rh–? ¿Cuántas veces más? Repite lo anterior, pero con una muestra de 1 000 personas (“Cantidad en la muestra” = 1000). Escribe abajo los resultados. TIPO DE SANGRE CANTIDAD TOTAL CANTIDAD RH+ CANTIDAD RH- O A B AB ¿De cuáles hay más: Rh+ o Rh–? ¿Cuántas veces más? Continúa con la toma de datos y algunos cálculos hasta que puedas responder las siguientes preguntas: ¿Qué porcentaje de los individuos es Rh+? ¿Qué porcentaje de los individuos es Rh–? Propuesta Hidalgo 1er Grado BIOLOGÍA 111
© Copyright 2026