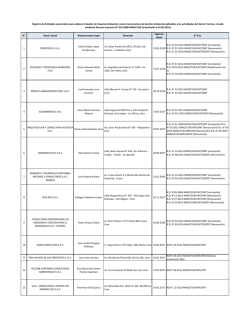
(n ∑ ∑ (i ) bi - U
UNIVERSIDAD DE CHILE
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS
ESCUELA DE INGENIERÍA Y CIENCIAS
Yerko Rowlands
TUTORÍA # 2:
TEOREMA DEL BINOMIO DE NEWTON Y CONJUNTOS NUMERABLES
P1. (P2 (a) 07-1 C4) Demuestre, sin usar inducción, que dado p ∈ R
Pn
k=1
n
k
pk (1 − p)n−k = pn ∀n ≥ 1
P2. (P1 (ii) 08-1 C4) Calcule en función de n el valor de la suma
(nk)
Pn
k=0 (k+1)(k+2)
10
P3. (P1 09-1 C4) En el desarrollo de (1 + x)16 ( xa2 − bx 3 )8 , a, b 6= 0
a) Determinar el coeficiente de x16
b) ¿Qué condición debe existir entre a y b para que no exista el término x16 ?
P4. (P1 11-1 C4)
a) Calcule el valor de la siguiente sumatoria para b ∈ R \{ 21 } fijo:
Pn Pi
i=0
i
j=0 j
bi
b) Considere el conjunto A 6= φ y se define
F = {f : {1,2,3} =⇒ A | f es función}
i) Demuestre que |F| = |A3 |
Indicación: Para f ∈ F considere la tupla (f (1),f (2),f (3))
ii) Demuestre que si A es numerable entonces F también es numerable
P5. (P2 b) 12-1 C4) Demuestre que el conjunto de todos los triángulos cuyos vertices
son elementos de Q × Q es numerable
1
© Copyright 2026