1. No category

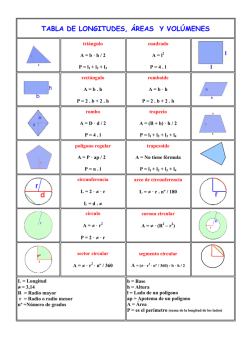
Grado 5
Clase:
Matemáticas
Unidad 2
Reconocimiento del proceso para calcular
el área de algunas figuras
Nombre:
INTRODUCCIÓN
El rey de la selva
En las siguientes imágenes se observa al rey león y a su amigo el mono analizando unos
planos sobre la selva, ellos intentan determinar sus medidas. Observa la imagen y responde
las preguntas.
Imagen 1. Plano de la selva.
¿Cómo podemos llamar a todo el territorio?
¿Será posible determinar la medida de la superficie? ¿Por qué?
Discute con tu docente que estrategia podría utilizar el león para hallar la medida de la superficie.
1
Grado 5
Matemáticas
Objetivos
Determinar estrategias para hallar el área de rectángulos, triángulos y círculos
Grado 5
Matemáticas
1.Cubre las siguientes figuras utilizando los cuadros de 1 cm2 y 1 m2 hasta completar su totalidad.
Representa los cuadros de 1 cm2 con color naranja y los de 1 m2 con color amarillo. Al final,
responde la pregunta que aparece en la parte inferior de la pantalla y continua con otro ejercicio.
1.Expresar medidas de área haciendo uso de las unidades de medida metro cuadrado y centímetro
cuadrado.
2.Determinar el área de figuras conformadas por cuadrados de 1 metro o 1 centímetro de lado.
3.Hacer uso de la expresión que le permite determinar el área de rectángulos.
4.Hacer uso de la expresión que le permite determinar el área de triángulos.
5.Determinar el área de polígonos irregulares descomponiéndolos en rectángulos y triángulos.
6.Hacer uso de la expresión que le permite determinar el área de círculos
ACTIVIDAD 1
Dibujando con cuadros
Al multiplicar la medida de dos de los lados del cuadrado de 1 cm, se puede terminar que el área
es de 1 cm2 y de forma similar, para el cuadrado cuyos lados miden 1 m, se puede determinar
que su área es de 1 m2.
Área= cm2
2
¿Cuántos cuadros utilizaste para cubrir toda la figura?
Área= m2
3
Grado 5
Matemáticas
Grado 5
Matemáticas
ACTIVIDAD 2
La maqueta de la ciudad
En la maqueta que construyó Daniela se pueden ver grandes edificios diseñados a escala.
Observa la imagen sobre la ciudad y las figuras que allí se forman.
¿Cuántos cuadros utilizaste para cubrir toda la figura?
4
Imagen 2. Edificios en la ciudad.
¿Qué figura geométrica puedes reconocer en cada una de las figuras?
5
Grado 5
Matemáticas
¿Cuántos apartamentos tienen el edificio, teniendo en cuenta que
cada ventana es un apartamento?
Grado 5
Matemáticas
3. Radio
4. Cancha de fútbol
¿Qué características crees que representan el número de pisos y
el número de ventanas en el primer piso teniendo en cuenta la
base y la altura?
Área:
Determina el área de las siguientes figuras
Área:
5. Cancha de tenis
1.Televisor
2. Celular
Área:
Área:
Área:
6
7
Grado 5
Matemáticas
Grado 5
Matemáticas
Si en los pasteles rectangulares decoraban la parte superior que tenía un área de 600 cm2, ¿Qué área se
debe decorar en un solo triángulo?
ACTIVIDAD 3
Pastelería
Al decorar los dos triángulos por separado, ¿las superficies sumarán la misma área que el rectángulo? ¿Por qué?
Al partir diagonalmente el pastel se pueden obtener dos pedazos de pastel con forma de
triángulos rectángulos
Recuerda:
Área = Largo x ancho/2
Determina el área de las siguientes figuras
1. Triángulo
2. Museo de Louvre
¿Crees que los dos triángulos tienen la misma medida de sus lados y forma? ¿Por qué?
Área:
8
Área:
9
Grado 5
Matemáticas
3. Pirámide
Grado 5
4. Señal de transito
Matemáticas
ACTIVIDAD 4
Figuras compuestas
Determina el área de cada figura simple y el área total de cada polígono.
a.
Área:
Área:
5. Escuadra
Área total del polígono:
Área del triángulo rectángulo:
Área:
Área del triángulo isósceles:
10
11
Grado 5
Matemáticas
Grado 5
Matemáticas
d.
b.
Área total del polígono:
Área total del polígono:
Área del triángulo rectángulo 1:
Área del rectángulo:
Área del triángulo rectángulo 2:
Área del triángulo isósceles:
Área del rectángulo:
c.
Área del triángulo escaleno 1:
Área total del polígono:
Área del triángulo rectángulo 1:
Área del triángulo escaleno 2:
Área del rectángulo:
Área del triángulo rectángulo 2:
12
13
Grado 5
Matemáticas
Grado 5
Matemáticas
Sabes ¿qué es el radio y qué es el diámetro?
c.
Radio
Diámetro
Área total del polígono:
Área del triángulo isósceles 1:
Área del rectángulo:
Área del triángulo isósceles 2:
El radio es la distancia que hay entre el centro del círculo y un punto del borde, y el diámetro es la distancia
entre un punto y otro en línea recta de la circunferencia pasando por el centro. Esto hace que el diámetro
sea dos veces el radio.
Además, se debe conocer que en la circunferencia se puede contener el diámetro una, dos, tres y un poquito
más de veces. A esta cantidad, que es aproximadamente tres come catorce, se le conoce como número pi.
ACTIVIDAD 5
3,14 = π
Conociendo el número pi y el radio, se puede determinar el área de cualquier círculo, de la forma
radio por radio por pi, lo cual ayuda a determinar la cantidad de masa necesaria.
El círculo y la circunferencia
Área = radio x radio x π
Circunferencia
Determina el área y el radio delas siguientes imágenes
El borde de esta forma es conocido
como circunferencia
1.
Área:
Mientras que el plano que está
limitado por la circunferencia
se conoce
Radio:
Círculo
14
15
Grado 5
Matemáticas
2.
Área:
Grado 5
Matemáticas
RESUMEN
Recordemos lo visto:
Radio:
1. Por medio de la superposición de cuadrados de 1 cm² y de 1 m² de área se puede determinar
el área de figuras.
3.
Área:
1 cm
2
1m
2
Radio:
4.
Área:
5 cm
2
Radio:
8m
2
2. Para determinar el área de un rectángulo se debe multiplicar la base por el ancho.
5.
Área:
Rectángulos
Largo
Ancho
Radio:
Área: Largo x Ancho
16
17
Grado 5
Matemáticas
Grado 5
3.El área de un triángulo en la mitad de la del cuadrilátero.
Matemáticas
TAREA
Triángulos
Escribe cómo podrías determinar el área del objeto mostrado y luego escribe tu respuesta usando
un decimal y escribiendo las unidades
Altura
1.
¿Cómo determinarías el área de la ventana?
Base
Base x Altura
2
Área:
4.Una circunferencia consta de círculo, circunferencia, radio y diámetro.
Radio
Círculos
Área total:
2.
¿Cómo determinarías el área de la puerta?
Diámetro
Circunferencia
5.El numero pi es la cantidad de veces que cabe el diámetro en la circunferencia y equivale a 3,1416.
π =3,14
6.Para determinar el área del círculo se debe tener en cuenta que es (radio x radio x pi)
Área total:
Área = radio x radio x π
18
19
Grado 5
Matemáticas
3.
Grado 5
Matemáticas
6.
¿Cómo determinarías el área de la estructura
metálica?
¿Cómo determinarías el área de la rueda
Área total:
Área total:
4.
¿Cómo determinarías el área del techo del
panteón
Área total:
5.
¿Cómo determinarías el área del balón
Área total:
20
21