1. No category

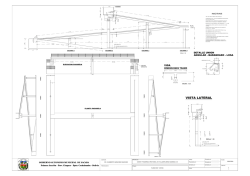
La línea de perfiles
|
Miembros en flexión trabes y vigas
ÍNDICE
1. Definición
2. Usos de miembros en flexión
3. Secciones transversales estructurales
convenientes
4. Comportamiento básico de miembros en
5. Clasificación de las secciones
6. Ejemplos de diseño de vigas
7. Referencias
structuras de acero se presentan los conceptos fundamentales del diseño de miembros
este tipo de elementos estructurales, se ilustran sus principales usos en estructuras de
ortamiento básico, se clasifican las secciones de acuerdo con sus relaciones
specificaciones AISC-2010; se indican sus modos de falla, los requisitos de diseño
s referidas y varios ejemplos típicos de diseño de vigas.
2. USO DE MIEMBROS EN FLEX
ÓN
elementos estructurales de sección prismática, colocados normalmente en posición
as perpendiculares al eje longitudinal (en cualquiera de sus dos sentidos) y producen
ones de flexión y cortante.
tf
k
B
T
tw
h
LBV
Vmáx
rza cortante
k
bf
La flexión es una de las acciones internas más comunes en las estructu
presenta en las vigas de los sistemas de piso, pero también en las vigas y
edificios industriales.
Las secciones más apropiadas para resistir flexión son las secciones “ I” lam
producida por cargas moderadas se utilizan perfiles estructurales laminado
momentos flexionantes de gran magnitud se recurre a miembros armados fa
eventualmente al uso de trabes armadas provistas de atiesadores.
En la flexión simple sujeta a carga uniformemente distribuida, la carga se a
produciéndose así, flexión alrededor del eje de mayor momento de inercia d
carga pasa por el centro de cortante de la sección, por lo que no produ
permanecen planas después de la flexión. En tales condiciones los esfue
siguientes:
tf
PERFIL IR
Mmáx
W = Carga uniformemente repartida kg/m.
L = Claro libre (longitud de la viga) m.
Vmáx = Fuerza cortante máxima kg.
Mmáx = Momento flexionante máximo kg - m.
LBM
ento flexionante
Solicitaciones de una viga típica con carga
iformemente repartida: flexión y cortante
Plano de carga
Patín en compresión
Miembro en flexión
Y
El problema de flexión aparentemente es muy sencillo de resolver, si no fuera
el pandeo lateral o pandeo lateral por flexo-torsión, ocasionado por la baja
dirección perpendicular al alma y por la ocurrencia de esfuerzos de comp
sección (patín comprimido), lo que ocasiona un problema de inestabilidad s
compresión axial.
Mx = Momento flexionante
Patín en tensión
Mx
Eje X
En el caso de una viga, el planteamiento y la solución del pandeo lateral
involucra a la torsión, lo que dá lugar a expresiones que contienen una gran
En trabes de gran peralte, aparecen problemas de pandeo local en los patine
puede arrugarse lo que dá lugar eventualmente a la necesidad de rigidiza
denominadas atiesadores.
n claro,
o, Gto.
dificio alto
apuato, Gto.
Y
Y
2 LI
2 LI
Y
X
X
Foto 2 Vigas laminadas IR,
edificio de atención ciudadana,
Gobierno del Edo. de Michoacán, Morelia, Mich.
X
Y
2
2 CE
Fig. 4 Secciones transversales típicas de miembros en
Teoría elástica simple para el diseño de vigas
Los principios fundamentales del diseño elástico son ampliamente utilizados a nivel
hace más de un siglo. Para entender las diferencias entre el diseño elástico y plás
empotrada y que soporta una carga uniformemente repartida. El diseño elástico se ba
y deformaciones.
El criterio de diseño de la viga estipula que los esfuerzos de flexión máximos en las f
la carga actuante, no deben exceder los esfuerzos permisibles de flexión estipulados
Fig. 4 Vigas de un sistema
de piso de un mezanine
ANSVERSALES
ES CONVENIENTES
siempre el de mayor momento de inercia (eje X- X), se requieren secciones estructurales de
como columnas flexo-comprimidas. Las vigas están sujetas preponderantemente a flexión
se cargan en el plano de simetría que corresponde al de menor momento de inercia.
Así, la viga tiene una reserva de capacidad a flexión y su comportamiento es elá
máximos (negativos) se presentan en los apoyos empotrados y en la sección me
flexionante máximo positivo, cuyo valor corresponde a la mitad del momento flexiona
Lo anterior significa que la viga todavía puede soportar carga; sin embargo, en el dise
las articulaciones plásticas en los apoyos y en la sección media de la viga, ya que es
W
A
B
L
LBV
Vm
Diagrama de fuerza cortante
perfiles de uso frecuente en vigas, siendo el más popular los perfiles IR laminados, ya que
ntes.
I se utilizan en vigas que soportan cargas de .gran magnitud
sversal distinta a la de los perfiles
levados y que pueden causar pandeo lateral por flexo-torsión. Las secciones de alma abierta
cuando se necesita espacio para canalizar las instalaciones eléctricas, hidrosanitarias o de aire
ga, o para cargas ligeras y grandes claros, como las cubiertas de naves industriales.
LBM
Mm
Diagrama de momento flexionante
edad de deformarse plásticamente después de alcanzar el punto de fluencia.
ansversales de una estructura alcanzan el esfuerzo de fluencia, éstas se mantienen al mismo
ón creciente, mientras que otras partes menos esforzadas se deforman elásticamente, hasta
ón de plastificación o fluencia.
Mp
Diagrama de momento
flexionante
L
Redistribución de momentos flexionantes
Diagrama de momentos correspondiente a la condición de colapso en el tram
S
form
Diagrama de momento flexionante correspon
condición de colapso en el tramo interior de una vi
Fig. 7 Redistribución de momentos flexionantes en un
ca carga-deflexión de una viga libremente apoyada
a una carga concentrada en la sección media
4. COMPORTAMIENTO BÁSICO
DE MIEMBROS EN FLEXIÓN
secciones transversales críticas de la viga alcanzan la condición de fluencia o plastificación, el
emente, debido a que solamente se necesita considerar este hecho.
ómo se redistribuyen los momentos flexionantes en la estructura sino solamente debe
e redistribuyen.
Los primeras investigaciones sobre el comportamiento de vigas ó miembros en flexió
siglo XV. A principio del siglo XVII, Galileo trabajó en el estudio de los esfuerzos prod
voladizo. Pero sólo dos siglos después, Navier formuló las ecuaciones de la flexión sim
del tiempo varias teorías más complejas con base en las investigaciones efectuada
flexo-torsión que las de Navier, su teoría sobre vigas es aún vigente para el diseño de
2θ
L/2
stica
θ
MP
Por otro lado, el efecto de la torsión en barras fue investigado a principio del siglo
tratamiento riguroso de la torsión, involucrando el alabeo y la flexión, fue propuesto
introdujo la analogía de la membrana, y en 1905, S. Timoshenko presentó los result
uniforme de las vigas de sección transversal
I”, “teniendo en cuenta la resistencia al des
la discusión sobre la torsión de secciones abiertas de paredes delgadas, y el efecto
vigas “I”. Algunos resultados no han sido aún incorporados en los métodos de diseño
La resistencia al pandeo lateral está íntimamente relacionada con la resistencia a
simultáneamente un estudio teórico sobre la estabilidad lateral en 1899, seguido de S
Consideró que la deformación plástica de los materiales dúctiles, St. Venant inició un n
Mp
clasifican en cuatro tipos en función de las relaciones ancho/grueso máximas de sus
n compresión axial, en compresión debida a flexión, en flexión o en flexo-compresión.
0.7
t
ompactas
Sx
Secciones
Secciones
no compactas
c
*0.38
E
fy
E
fy
λpf
0
1
*1.0
Re ión ancho/grueso,
Seccio
λrf
lac
λ= bf / 2t f
Fig. 9 Curva de momento plástico versus relacion ancho
Mx
Se considera en la figura anterior el caso de secciones estructurales en las que a
compacto o esbelto.
L
• Secciones tipo 1 = compactas
• Secciones tipo 2 = compactas
• Secciones tipo 3 = no compactas
• Secciones tipo 4 = esbeltas
8 Clasificación de las secciones de acero
ara diseño plástico y para diseño sísmico) pueden alcanzar el momento plástico en vigas, y el
resión en barras flexo-comprimidas, y conservarlo durante las rotaciones inelásticas necesarias
en la estructura, y para desarrollar las ductilidades adoptadas en el diseño de estructuras
En este caso, los factores de reducción de la resistencia y de seguridad
φ=( 0.90 y Ω
pero es necesario tener en cuenta, además de los estados límite de plastificació
mencionados, el estado límite de pandeo local de los elementos que componen la se
Para que una sección clasifique en uno de los tipos, todos los elementos planos
relaciones ancho/espesor propias de ese tipo.
ompactas y para diseño sísmico) pueden alcanzar el momento plástico como las secciones tipo
otación inelástica limitada, aunque suficiente para ser utilizadas en estructuras diseñadas
antemente estáticas, y en zonas sísmicas, con factores de comportamiento sísmico reducidos.
o compactas) pueden alcanzar el momento correspondiente a la iniciación del flujo plástico en
rotación inelástica. La falla de estas secciones ocurre por pandeo inelástico de uno de sus
uando las solicitaciones han sido determinadas por un análisis elástico y las cargas son
esbeltas) tienen como estado límite de resistencia el pandeo local elástico de alguno de los
. Estas secciones no son capaces de desarrollar el momento plástico de la sección y no tienen
pandeo.
elementos planos de los dos primeros tipos de secciones definidos arriba no deben exceder los
SECCIÓN bf 2/ t f
E
fy
f y(k
ASTM A36
2,530
10.8
Compacta
0.38
No compacta
1.0
E
fy
28.4
Esbelta
1.0
E
>28.4
lo que asegura que las secciones de los tipos 1 y 2 podrán alcanzar sus estados límite de
menos prematuros de pandeo local.
n elemento excede los límites correspondientes a las del tipo 1 y 2 son tipo 3.
V
2
ADMISIBLES
g/cm
)
de esfuerzos en la sección por debajo del esfuerzo de fluencia (pandeo local elástico) y una última
e cuando la sección está parcialmente plastificada.
o/grueso intermedias, las Especificaciones AISC consideran una transición lineal entre el momento
fluencia.
ta, es necesario modificar las expresiones del momento crítico de pandeo lateral por flexo-torsión
ar el pandeo inelástico del alma.
a) Cubre placa
b) Placa en los
centros de
los patines
bros en flexión
de falla de los miembros en flexión.
a un estado límite de la sección transversal del miembro en flexión. Los aceros dúctiles se pueden
durecimiento por deformación, como un material elástico que al llegar a la fluencia se comporta
de esta manera en un miembro estructural en flexión, es necesario que no ocurran fenómenos de
a.
y patines de perfiles IR utilizados como vigas
de inestabilidad en el estado elástico o inelástico que afecta los elementos planos que forman la
o estructural (viga o columna) comprimidos en sus planos. Produce deformaciones importantes que
con perfiles estructurales laminados de sección transversal se deforma más allá del límite elástico,
ndeo local de los patines o del alma.
y columnas. Dependiendo de la relación de esbeltez de los elementos que componen la sección
s elementos que están en compresión debido a la flexión fallen por inestabilidad local, ocasionando
a para mantener la forma de su sección transversal, su resistencia a la flexión se reducirá; el pandeo
que la sección soporte el momento plástico, durante un tiempo suficiente para que se formen en
nes plásticas.
el requisito de la capacidad de deformación (rotación adecuada bajo momento plástico), los
viga (patines) deben tener una relación ancho/grueso suficiente para impedir el pandeo local
ndeo local del alma, las especificaciones de diseño estipulan relaciones peralte/grueso del alma que
como vigas.
os perfiles estructurales laminados comerciales satisfacen el requisito de relaciones ancho/grueso
compacta)
adas con placas soldadas que no cumplan con las relaciones ancho grueso de patines pueden
donde se forman eventualmente las articulaciones plásticas.
Pandeo lateral
El efecto del pandeo lateral es similar al del pandeo local. De hecho, en muchas prueba
IR se presentan simultáneamente.
También puede considerarse que el pandeo lateral está impedido cuando el sistema d
de la estructura, están formados por láminas de acero acanaladas sujetas al patín co
Rotación
ción
El pandeo lateral no puede presentarse, cualquiera que sea la longitud libre, en vig
maciza o hueca, de cualquier tipo, o cuando la flexión se presenta alrededor del eje
transversales; en todos esos casos las vigas son estables desde el punto de vista de
El problema consiste en determinar cual es la resistencia al pandeo lateral de un tram
y en segundo lugar, debe determinarse la rotación requerida en una articulación plá
pueda alcanzar la carga última calculada.
(rad/m)
penderá de la clasificación de la viga. A continuación se presentan estos modos.
Obviamente estas recomendaciones aumentan el costo de la estructura, debiéndose
de que el problema no se resuelve con otro perfil o existe alguna restricción, por e
respecto que la sección “IR en cajón” (fig. 10 e). Tiene la ventaja de poseer un fac
sustancialmente la resistencia al pandeo lateral.
La siguiente figura muestra la relación momento curvatura indeseable; el momento
rotaciones suficientemente grandes. Este resultado se obtuvo en un ensaye realizado
apoyada, sometida a cargas concentradas aplicadas simétricamente y con un claro int
el pandeo lateral prematuro.
2500
s (kg - m)
ón.
d) A
v
Fig. 10 Formas de rigidizar perfiles tipo IR para evitar in
1875
P
P
1250
Mom
en
to
o del alma.
c) Atiesador
longitudinal
0.3L
625
0.4L
L
0.3L
0
0
10
20
30
40
50
6
rigidez a la flexión en el plano de la misma es muy grande con relación a su rigidez la
v
u
En efecto, en vigas o trabes que tienen una longitud considerable y poco espesor, e
menor que el necesario para agotar la resistencia del material. Esto indica que en este
la falla se ha producido por inestabilidad del miembro.
De la analogía del miembro en compresión, es posible ver que la resistencia al pan
depende del tipo y espaciamiento de los soportes laterales del patín comprimido de la
o
Ø
Posición final
en el plano
de flexión
A
yLB
M
M
A-A
A
A
C LB
Fig.12 Pandeo lateral de vigas
M
M
s con los que se proporciona soporte lateral a las vigas de acero deben impedir
azamiento lateral y el giro de las secciones transversales.
A
ección transversal I
A
M
M
el diseño de miembros en flexión, fabricados con perfiles de sección transversal. La figura
carga transversal y que produce flexión; compresión en el patín superior y tensión en el patín
A
idan el desplazamiento lateral del patín superior, esta placa se deforma de la misma manera
mpresión axial. El patín inferior evita el desplazamiento lateral del patín superior, ya que éste no
mido de una viga es adecuado, la resistencia de diseño en flexión está regida por la resistencia
den fallar por pandeo local; en caso contrario, la controla el pandeo lateral por flexo-torsión.
sión
A
M
Soporte lateral
M
A
2-2
Soporte lateral
Patín de Compresión
derar es el pandeo lateral por flexo-torsión de la viga. Es un modo de pandeo de un miembro
torsión, de ahí su nombre.
dera una viga libremente apoyada de longitud L sometida a un momento uniforme M, cuyos
lateralmente exclusivamente en los apoyos.
se la parte comprimida de la sección como un miembro en compresión. A medida que aumenta
en este miembro se incrementa, hasta alcanzar la carga de pandeo. Si consideramos que la
ejes 1-1 y 2-2 (fig. 13), el patín comprimido debería pandearse alrededor del eje 1-1, ya que
n embargo, la parte en tensión de la sección restringe ese movimiento y, por tanto, el patín
2-2. Debido, nuevamente, al efecto de la parte en tensión, el pandeo del patín comprimido no
además de desplazarse. Este fenómeno de inestabilidad es lo que se conoce como pandeo
Planta
Fig. 13 Modos de pandeo en vigas sometidas
a flexión pura bajo la acción de pares iguales en ma
y de sentidos contarios, aplicados en sus extrem
Las siguientes figuras ilustran los fenómenos de inestabilidad descritos anteriorme
secciones compactas mantengan la forma de su sección transversal y retarden algu
deformaciones plásticas, en el caso de secciones esbeltas puede presentarse no sola
en flexión. La primera clasificación es de acuerdo al tipo de soporte lateral. Dependiendo
pueden dividir en: vigas con soporte lateral adecuado, aquellas que están soportadas later
viga no falle por inestabilidad global, y vigas sin soporte lateral: no poseen suficientes
inestabilidad global.
Para evitar el pandeo lateral de una viga, es necesario revisar si la separación propuesta
Cuando la distancia entre puntos soportados lateralmente es mayor que la distancia
u queL e
estado límite de falla de vigas de sección transversal
oI H flexionadas alrededor de los ejes
pandeo lateral por flexo-torsión, que ocasiona disminuciones, en la resistencia a la flexión
esbeltas pueden presentarse fallas prematuras por pandeo local, bajo solicitaciones más
X
Se distinguen dos tipos de soportes laterales de vigas:
1. Soporte lateral continuo: El patín está soportado lateralmente en toda la longitud
el patín comprimido (patín superior) está soportado lateralmente de manera continua p
el patín
2. Apoyo lateral puntual: El patín comprimido de la viga está soportado lateralmente en
secundarias proporcionan soporte lateral a las vigas principales en un sistema de piso
los largueros proporcionan soporte lateral a las vigas de techo en estructuras industria
Y
X
X
Factores que influyen en la resistencia al pandeo lateral por fle
Existen varios factores que afectan la resistencia al pandeo lateral por flexo-torsión elást
mencionarse los siguientes:
1. Condiciones de apoyo de la viga:Influyen tanto para flexión como para torsión.
Y
pandeo local del alma
X
el alma
2. Soportes laterales intermedios: La presencia de soportes laterales intermedios dismi
el momento crítico de pandeo lateral por flexo-torsión aumenta.
3. Relación de inercias:Es posible demostrar que cuando la inercia del eje de flexión es
pandeo lateral por flexo-torsión no ocurre. De esta manera, para flexión respecto al ej
pandeo lateral por flexo-torsión no es aplicable.
4. Tipo de cargas aplicadas:La deducción de la ecuación de resistencia nominal fue hec
uniforme, que es el caso más desfavorable, ya que todo el patín comprimido está some
viga. Para casos en que el diagrama de momentos no es constante, se puede demo
flexo-torsión es mayor.
5. Punto de aplicación de la carga: El momento crítico de pandeo lateral por flexo-torsi
aplicada en el patín superior, el centroide o el patín inferior de la sección.
Una viga puede fallar por pandeo lateral por flexo-torsión inelástico debido a varias causa
Si la longitud no soportada lateralmente de la viga es menor que un determinado valor
momento crítico de pandeo lateral por flexo-torsión elástico va a ser mayor que el mome
lateral por flexo-torsión elástico y la viga comienza a plastificarse. Al plastificarse parcialm
que puede generar el pandeo lateral por flexo-torsión de la sección. El momento crítico en
eométricas iniciales de la viga, así como las excentricidades que las cargas generan momentos,
sde un principio. Esto también redunda en que la capacidad al pandeo lateral por flexo-torsión de la
ga ideal.
rtadas lateralmente
considerar el pandeo local, va a estar definido por la distancia entre soportes laterales o longitud no
dos valores límite que se deben considerar:
lateralmente máxima para lograr que la viga alcance el momento plástico y tenga capacidad de
s de este punto.
El diseño de miembros en flexión conforme a las Especificaciones AISC- 2010 consid
fluencia, pandeo local de los patines, pandeo local del alma y pandeo lateral por fle
aparecían de manera implícita o explicita en las Especificaciones AISC-ASD-1989
esfuerzos permisibles.
El estado límite de fluencia o plastificación rige el diseño de vigas compactas cuyos
lateralmente en forma continua para evitar el pandeo lateral por flexo-torsión. La resis
momento plástico, que se determina con la ecuación (F2-1) de las especificaciones A
a partir de la cual la viga fallará por pandeo lateral por flexo-torsión elástico.
or flexo-torsión va a depender de la distancia entre soportes laterales.
menores que pL, el estado límite de plastificación controla o domina.
eralmente
b, L
eralmente Lb, mayores o iguales que Lr, el estado límite de pandeo lateral por flexo-torsión elástico
Está dada por el momento crítico de pandeo lateral por flexo-torsión elástico, multiplicada por el factor
orma del diagrama de momento.
e obtenerse igualando el momento crítico de pandeo lateral por flexo-torsión
M Mp. El valor
cr con
debe ser
tiza que la viga tenga capacidad de deformación inelástica y, por lop tanto,
L menor que ese
sistencia de una viga
En las especificaciones anteriores del AISC, en el diseño por esfuerzos permisibles (A
de los módulos de sección plástico y elástico (factor de forma),
Zx/ Sx se tomaba conserv
resulta para secciones que cumplen el criterio de sección compacta un esfuerzo de fle
constituyen las secciones transversales de los miembros en flexión tienen relaciones ancho/grueso
o local no es crítico, y el patín comprimido de la viga está soportado lateralmente en forma continua, o
os para que el pandeo lateral tampoco lo sea, los estados límite de falla corresponden al agotamiento
nte o una combinación de ambas solicitaciones, y se presentan sin que la viga se salga del plano que
án aplicadas las cargas, y sin que se deformen sus secciones transversales.
Lo anterior demuestra que las Especificaciones AISC-ASD 2010 coinciden con las ant
límite de plastificación o fluencia.
ntes de un miembro en flexión son por formación de un mecanismo con articulaciones plásticas,
flexión en la sección crítica, en miembros que no admiten redistribución de momentos, iniciación del
plastificación del alma por cortante, o por flexión y cortante combinados.
Las nuevas especificaciones AISC-2010 permiten al diseñador estructural aprovecha
permite obtener resistencias hasta del 20 % mayores (aproximadamente el 80 % del e
En el caso del método de diseño con LRFD, las especificaciones de diseño de 1999
fluencia son idénticas.
xión deben considerarse también los estados límite de servicio de deformaciones excesivas y de
de todas las estructuras de acero, por ejemplo, el de corrosión y fatiga.
rededor de los ejes centroidales y principales de mayor momento de inercia de las secciones
elementos exteriores que impidan el desplazamiento lateral del patín comprimido, las vigas tienden a
el pandeo lateral por flexo-torsión constituye el estado límite de falla.
es especialmente crítico en vigas cuyas secciones transversales tienen un momento de inercia
veces mayor que alrededor del otro eje centroidal y principal, si además, su resistencia a la torsión es
r flexo-torsión suele ser más importante en vigas de secciónI
, sobre todo sí son de gran peralte, que
acas soldadas (secciones en cajón).
o iguales quer,Lel estado límite de pandeo lateral por flexo-torsión elástico
eralmente,
L
b mayores
Ésta está dada por el momento crítico de pandeo lateral por flexo-torsión elástico, multiplicado por el
efecto y la forma del diagrama de momento flexionante en la viga. Para longitudes no soportadas
esistencia está dada por una transición lineal entre
p yMMr el momento de primera fluencia
s.
Estado límite de pandeo lateral por flexo-torsión
Se presenta en miembros en los cuales la longitud no soportada lateralmente del pa
grandes. La ecuación que proporciona la capacidad nominal de un miembro en f
longitudes límites Lp y Lr es una línea recta.
Para vigas con soportes laterales a distancias mayores que
L utiliza una ecuación de
r se
Las especificaciones AISC-2010 describen la resistencia de una viga no soportada
cada una con sus propios límites de aplicación. Las especificaciones AISC-ASD 19
cuales debían en primer lugar ser evaluadas para posteriormente elegir el mayor valo
En las especificaciones anteriores, las trabes armadas hechas con tres placas soldad
cual es igual a 0.7 veces el momento de iniciación
presentan un cambio en la determinación de
r el M
s decir, supone que la magnitud máxima de los esfuerzos residuales es un 30% del esfuerzo de
de si se trata de secciones estructurales laminadas o soldadas (fabricadas con tres o cuatro placas
En las especificaciones AISC 2010 todas las especificaciones de miembros en flexión
la única excepción de una sección específica destinada a la determinación de las rel
planos que constituyen la sección transversal de la viga.
dad de que almas o patines se pandeen localmente, pues este fenómeno, característico de secciones
sionar por sí solo o en combinación con pandeo lateral, el agotamiento de la resistencia.
Las vigas armadas, junto con la incorporación de las disposiciones para secciones
capítulo F bastante extenso pero completo para fines de diseño estructural.
, con o sin consideración de efecto de campo de tensión diagonal, quedan incorporadas en
nominaln queda
V
expresada como se muestra en las ecuaciones siguientes:
dos con almas atiesadas o con almas no atiesadas
(G2-1)
v
h
tw
con
Ωv
2.24
E
fy
C v = 1.
= 1.5 (ASD)
estos miembros soporten cargas de magnitud elevada o que las cargas estén próximas a
Las deflexiones o flechas son un estado límite de servicio que debe verificarse en cualqu
trabes de gran claro.
El claro de las trabes o vigas es el parámetro que más influye en el valor de la deflexión.
cual está elevado a la tercera y cuarta potencia. Los otros parámetros son el módulo de ela
la viga y la forma de su sección transversal, con la que se determina el momento de inerci
mayor resistencia.
Las vibraciones, ocasionadas por el tránsito de las personas, constituyen un estado límite
un diseño inadecuado de las trabes o vigas que forman parte de los sistemas de piso com
funcionamiento correcto de la estructura durante su vida útil.
Las vibraciones dependen de las características dinámicas del sistema de piso: frecuenc
dos con simetría simple y canales, excepto tubos circulares el coeficiente de corte del alma
Deberán tomarse las precauciones necesarias para reducir las vibraciones a límites toler
C v = 1.0
≤ 1au.37
C )b
kv E
fy
Cv =
k E
1.10 v
fy
h
tw
1.51k v E
Cv =
h
tw
f
y
n
Diseño de miembros en flexión (vigas).
Diseño por cortante.
Clasificación de las secciones de acero para pandeo local.
También es aplicable a barras de sección transversal maciza, circular, cuadrada o
alrededor de su eje de menor momento de inercia, y a barras de sección transversal c
v , se define de la siguiente manera:
h
tw
Capítulo F
Capítulo G
Sección B4
Este capítulo es aplicable a vigas laminadas y trabes hechas con placas soldadas, de
ejes de simetría, cargadas en uno de los planos de simetría, y a canales.
2
) )
Extracto de las ecuaciones de las Especificaciones AISC-2010
o miembros en flexión
< 260
Requisitos de resistencia
≤φb M n
M uLRFD)
Flexión
Ma ≤
k v = 5.0
Mn
Ωb
(
(ASD)
perfiles T donde:k v = 1.2
Cortante
h≤
260
ah
) )
2
kv = 5 +
) )
Va ≤
5
(
Vn
(ASD)
Ωb
2
) a h)
2
260
auC
a dhn<
ah
VuLRFD)
≤φvVn
k v = 5.0
o para asegurar que la resistencia a esfuerzos cortantes de un perfil laminado en las
la misma que se utilizaba en las Especificaciones ASD1989. En términos de esfuerzos
, que
esfuerzo cortante de 0.4
f es el valor tradicional, lo cual se traduce en un pequeño
Factores de reducción de resistencia en flexión y coeficientes de seguridad para miem
φb = 0. 90
φv = 1.00
(LRFD)
(LRFD)
Ω b = 1.67 (
Ω v = 1.50 (
La resistencia de diseño en flexión depende de las longitudes
b, Lp y Lr de la forma de
residuales es un 30% del esfuerzo de fluencia, independientemente de si se trata de
2. Sí
tados límite siguientes:
Lp < Lb L
r
Para el caso de perfiles d
I e patines no compactos, la resistencia nominal en flexión es
momento plástico y el momento de iniciación de la fluencia. Si la sección tiene un eje
de aplicación de las cargas, es necesario modificar los momentos plástico y de fluen
en cuenta el efecto del pandeo inelástico del alma inducido por el pandeo del patín.
os patines
or flexo-torsión
f
minal de vigas de sección compacta. El factor de reducción de la resistencia
φb = 0.90 y el
os límite o modos de falla a considerar son plastificación de la sección. En el caso de perfiles
acidad por plastificación es el momento plástico de la sección, calculado como el esfuerzo de
sección plástico
Zx de la sección correspondiente respecto al eje en que se aplica la flexión.
El factor de modificación por pandeo lateral torsional o coeficiente de flexión,
b C
Cb =
Mn = f y Z x
(F2-1)
Plastificación
dos alrededor del eje de menor momento de inercia, el modo de falla por pandeo lateral por
lexión es alrededor del eje de menor resistencia del miembro. Por tanto, el único modo de falla
ción.
2.5M máx
12.5M máx
Rm
+ 3M A + 4 M B + 3M C
3 .0
W
A
B
A
L
MA
MB
M
MC
MA
M máx
LBM
P
W
A
B
L
A
L
MA MB MC
MA
M
LBM
Pandeo lateral por
flexotorsión
inelástico
Lp
Pandeo lateral por
flexotorsión
elástico
Lr
L
ngitud no soportada lateralmente, L b
ento resistente nominal - longitud no soportada lateralmente
deran tres zonas para la determinación de la resistencia nominal en flexión, cuando no hay
mera zona corresponde a tramos de vigas que tienen una longitud entre soportes laterales menor o
la plastificación total de la sección transversal. La segunda zona corresponde a aquellos miembros
cuyaL capacidad está determinada por el pandeo lateral por
on separaciones mayores o iguales rque
ona corresponde a distancias entre soportes laterales intermedios, en los que la resistencia está dada
elástico. Debido a las dificultades en incluir los efectos de las imperfecciones geométricas de los
eterminación de la resistencia al pandeo lateral por flexo-torsión inelástico, el AISC optó por utilizar
Fig. 16 Diagramas de momento flexionante para
del factor de modificación para el pandeo lateral
Mmáx, valor absoluto del momento flexionante máximo en la viga, en T-m.
MA, MB y MC, son los valores absolutos de los momentos flexionantes en el primer cu
respectivamente en T-m.
R para
Rm, parámetro adimensional que depende de la forma de la sección transversal
m = 1.0
para miembros con un eje de simetría que se flexionan en curvatura doble
El objeto del coeficiente Cb es incluir en las ecuaciones de las especificaciones AISC-20
de manera aproximada, la influencia de la ley de variación del momento flexionante sobre
SOPORTE LATERAL A LO LARGO
DEL CLARO DE LA VIGA
Ninguno
uniforme y, efectivamente aumenta la separación máxima entre soportes laterales qu
de la viga esté regida por plastificación de sus secciones transversales.
1.32
En los puntos de aplicación de
las cargas concentradas
1.67
Fcr =
1.67
2
π
E
( (
2
Cb
Lb
rts
( (
Jc Lb
1+ 0.078
S x ho rT
2
:setneiugis senoicauce sal noc naluclac es rL y pL
Ninguno
1.14
En los puntos de aplicación de
las cargas concentradas
1.67
Ninguno
L p = 1.76ryy
1.00
E
fy
Cuando la sección tiene elementos no compactos, la ecuación del momento crítico ca
Lr también son diferentes. En este caso,
r el radio de giro del área formada por el pa
t es
alma comprimida y wa es el cociente del área de alma comprimida entre el área de los
1.67
1.14
1.11 1.11
En los puntos de aplicación de
las cargas concentradas
1.67
1.67
Donde:
Para Perfiles I
Ninguno
c =.-1.0
pf
Para Canales
En la sección media
(centro del claro)
1.30
(F2-8b)
1.30
rT puede interpretarse como el radio de giro del área formada por el patín comprimido má
La resistencia al pandeo lateral por flexo-torsión depende de la distancia entre soporte
lateralmente, L
b menores que L
p el estado límite de flujo plástico (plastificación) rige el diseñ
Pandeo por flexo-torsión
(F2-2)
Cb = 1.0 (Resistencia básica)
Lr
f y Sx
FT
almente en el patín en compresión, L b
n
COEFICIENTE
Cb
Pandeo
elástico
LFT
Las especificaciones AISC-2010 consideran tres zonas en la determinación de la resist
consideraciones de pandeo local. La primera región corresponde a miembros con una dis
a Lp, cuya capacidad está dada por la plastificación de la sección. La segunda región c
distancia entre soportes laterales es mayor o igual que
L capacidad está determinada
r cuya
elástico. La tercera y última región corresponde a distancias entre soportes laterales interm
pandeo lateral por flexo-torsión inelástico. Debido a las dificultades en incluir los efectos d
en la determinación de la capacidad por pandeo lateral por flexo-torsión inelástico, la AIS
Mp y Mr para este rango de longitudes no arriostradas.
La última edición de las Especificaciones AISC-2010 incluye ecuaciones únicas para e
deben ser multiplicadas por el factor de reducción de la resistencia o divididas por el factor
LRFD o esfuerzos permisibles (ASD).
Miembros de sección transversal I con dos ejes de simetría con alm
compactas, o patines esbeltos flexionados alrededor de su eje de m
1
λ λ
2.- λ pf <
M n = f y Z xx
[
(
M n = M p - ( M p - 0.7 f y S x (
λ - λ pf
λ rf- λ pf
([
Mp
s estados límite siguientes
mpresión
ón
rimido
sión
R pc =
(F4-1)
R pc f y S xc
(
M yc
-
(
Mp
M yc
( (λλ−λ λ ( [
-1
pw
rw
b fc
Lb - L p
Lr - L p
([
R pc M yc
(F4-2)
h
1
h2
12 o + a w
d 6 ho d
-
pw
Mp
(F4-9
M yc
(
(F4-11)
(
Donde:
b fc es e
t fc es e
a
h t
aw = c w
b fc t fc
límite adicional que corresponde a la fluencia de los patines, ya que si un patín se plastifica, el
ea inmediatamente.
- ( R pc M yc - FL S xc (
Mp
Para perfiles I :
rT
c
[
(F4-12)
w
es e
com
2. Pandeo local del patín comprimido
2.1. Para secciones con patines no compactos
(F4-3)
M yc
0.5f
(F4
(F4-4)
2.2. Para secciones con patines esbeltos
En el caso de perfiles I de patines esbeltos, la resistencia está dada por el momento c
(F4-5)
Mn =
0.9 Ek c S xc
λ2
2.3. Flujo plástico del patín en tensión
M n = R pt M yt
(F4-14)
(F4-15)
Donde:
M yt = f y S xt
(F4-6a)
El factor Rpt está dado por la siguiente ecuación:
y
iS
(F4-6b)
a) Cuando
λ pw
R pt =
a el estado límite de plastificación.
Mp
M yt
b) Cuando
hc
< λ pw
tw
(F4-16a)
(F4-7)
Miembros I con dos ejes de simetría y con un solo eje de sime
flexionados alrededor del eje de mayor momento de inercia
ímite de pandeo lateral por flexo-torsión
cuación:
hc
tw
1. Flujo plástico del patín comprimido
(F4-8)
Cuando Lb
.-
L
p
M n = R pg yf S xc
2. Pandeo lateral por flexo-torsión
(F5-1)
p
Perfiles T y TL, formados por dos ángulos en espalda, son secciones que tienen un so
en este eje, la resistencia nominal está dada por los estados límite de plastificación y p
.3 f
y
(
Lb - L p
)
Lr - L p
([
f
y
(F5-3)
Lr = rT
R pg = 1 -
f
(F5-4)
y
aw
E
0.7 f
(F5-6)
y
(
aw
hc
E
- 5.7
1200 + 300a w t w
fy
(
1.0
10
En el caso de la plastificación, el momento plástico está limitado a 1.6 veces el mome
alma se encuentra preponderantemente sometida a tensión y, ya siM es que ésta s
compresión. Esta diferencia toma en cuenta la mayor inestabilidad del alma de la se
considera un factor Cb igual a 1 para cualquier forma de diagrama de momento.
Como el alma se encuentra en o muy cerca del eje de flexión, sólo se considera la ocu
1. Fluencia ó plastificación
Cuandoλ
λ pf
Mn = M p = f yZy
ompresión
1.6 f y S y
(F6-1)
2. Pandeo local en los patines
a) Patines no compactos
(F5-1)
Cuando λ pf < λ
λ rf
[
M n = M p - (M p - 0.7 f y S y
mido
(F5-7)
y
(λ λ ( [
) λ- λ
rf
-
pf
M n y= Fcr S
(F5-8)
pf
rf
-
pf
λ pf
([
(F6-2)
λ < λ rf
cambia dependiendo de si los patines pueden pandearse elástica o inelásticamente. Para el
o (es decir, patines no compactos), la ecuación que proporcionan las especificaciones
eal entrey fy el esfuerzo correspondiente al momento de iniciación de fluencia.
3f
(λ
b) Patines esbeltos
Cuando
λ pf < λ λ rf
) λ- λ
(F6-3)
(F6-4)
Secciones estructurales huecas hss cuadradas y rectangulare
En el caso de secciones estructurales huecas, cuadradas y rectangulares con patines
el momento de pandeo lateral por flexo-torsión inelástico asociado a ambos casos y se
ancho grueso, se utiliza la transición lineal (en función de la relación ancho/grueso de
(F5-9)
tw
0.76
1. Plastificación o fluencia
Mn = M p = f yZ
(F7-
2. Pandeo local de los patines
ensión
(F7
3. Patines esbeltos
c
M n = f y Se
(F7
(F7-4)
fyS
()
0.305
h
tw
f
y
E
- 0.738
(
Perfiles T y TL (T formados por dos ángulos en espalda). Son secciones que tienen
está aplicada en este eje, la resistencia nominal en flexión está dada por los estados
por flexo-torsión.
En el caso de la plastificación, el momento plástico está limitado a 1.6 veces el mo
sección My si es que el alma se encuentra sometida principalmente en tensión yyasiMse
compresión. Esta diferencia refleja la mayor inestabilidad del alma de la T. Para cons
el coeficiente de flexión Cb igual a 1 para cualquier forma de diagrama de momento
Mp
(F7-5)
1. Plastificación de la sección
Mn = M p
a) Alma en tensión
HSS (tubos circulares)
1.6 M y
Mn = Mp = f yZx
as, circulares, cuadradas o rectangulares, los momentos de inercia de la sección respecto a sus
arecidos. Por lo tanto, el estado límite de pandeo lateral por flexo-torsión no se alcanza.
s secciones tubulares compactas está dada por el estado límite de flujo plástico solamente.
(F8-1)
(F9-1)
Z
(F9-2)
b) Alma en compresión
Mp = f yZx
(F9-3)
My
2. Pandeo lateral por flexo-torsión
La capacidad al pandeo lateral por flexo-torsión es igual al momento crítico elástic
considerando la diferencia en resistencia cuando los extremos del alma están en tens
y
[
M n = M cr =
S
(F8-2)
Donde:
B = ± 2.3
caso de perfiles tubulares redondos depende de la relación diámetro espesor. Para secciones
rcano al momento plástico, pero la resistencia decae lentamente después de la formación de
es el resultado de cinco investigaciones experimentales en el comportamiento de secciones
EI y GJ
( (
d
Lb
Lb
Iy
J
[B +
1+ B2
[
(F9-4)
(F9-5)
El signo positivo se aplica cuando el alma está en tensión y el negativo cuando está
3. Pandeo local del patín de perfiles T
a) Secciones no compactas
(F8-3)
b) Secciones esbeltas
xpresión de la tensión crítica está basada en resultados experimentales.
(F8-4)
Para perfiles T y TL, la resistencia se expresa como un esfuerzo crítico multiplicado
donde el esfuerzo se calcula utilizando la ecuación del esfuerzo de pandeo local e
extremo y libre en el otro.
Lo mismo ocurre en el caso de ángulos aislados, excepto que el módulo resistente se
el aumento de los esfuerzos calculados utilizando las propiedades geométricas, en
biaxial.
(F9-11)
tructura deba tomarse en cuenta, las Especificaciones AISC-2011 contienen las siguientes
elástico está dado por una ecuación más simple. Debe notarse que en ambos c
considerada a través del factor bCaplicado al momento crítico elástico, en lugar de la re
tificación o por pandeo lateral por flexo-torsión. En el caso de plastificación, la capacidad se
e iniciación de la fluenciay, M
donde My se calcula para el eje de flexión. El factor de forma de
e cualquier eje excede 1.5, así es que se determinó utilizar este valor como un límite inferior
n.
En el caso de ángulos de lados desiguales flexionados respecto al eje principal mayor
del factor w.
(F10-1)
eralmente en forma continua, el es ado límite de plastificación controlará el diseño. Si no es
ral por flexo-torsión está dada por el momento crítico elástico
M
en un 25% para
E, reducido
ón, si es que el pandeo lateral por flexo-torsión ocurre en el rango elástico, o se toma una
My
y el momento de plastificación 1.5M
y, si es que el pandeo lateral por flexo-torsión es
(F10
Este factor depende de la posición del centro de torsión respecto de los ejes principale
aplicado. Si el centro de torsión está comprimido,
e es máxim
w es positivo y el momento M
momento crítico es reducido. Si el diagrama de momentos cambia de signo en el tra
conservadoramente la resistencia asociada al
w negativo. El factor w es independiente d
pág. 16.1 - 322, de los comentarios de las Especificaciones AISC-2010 proporciona v
w para diferentes tamaños de ángulos. Para flexión respecto al eje principal menor, =
Finalmente, si la flexión se aplica alrededor de uno de los ejes geométricos de u
descomponer la carga en los ejes principales y considerar el problema de flexión biax
Me
y
(
My
Me
2. Pandeo local de las alas
(F10-2)
Me
a) Patines no compactos
(
My
1.5M y
(F10-3)
(( (
b
t
f
y
(F10-
E
b) Patines esbeltos
e pandeo lateral por flexo-torsión elástico
M
del tipo de ángulo, el eje de flexión y
e depende
andeo lateral por flexo-torsión.
Para el caso de secciones asimétricas, se debe evaluar adicionalmente el estado de p
requiere un análisis especial para determinar el esfuerzo crítico correspondiente.
M n = Fcrc S
Fcr =
(F10-6a)
(F10-
0.71E
((
b
t
(F10-
2
Barras rectangulares y redondas
(F10-6b)
onado alrededor de un eje geométrico, sin restricción al pandeo lateral por flexo-torsión, se
principales. Esta flexión biaxial genera esfuerzos en la sección que pueden ser hasta un 25%
ilizar las propiedades geométricas con respecto a los ejes geométricos. Las Especificaciones
para poder estimar la capacidad de la sección sin necesidad de descomponer la flexión en los
restringido lateralmente en el punto de momento máximo, es posible tomar ventaja de un
de pandeo lateral por flexo-torsión elástico y utilizar el momento de iniciación de la fluencia
M
y
nde a un eje geométrico.
e mayor momento de inercia de ángulos de lados iguales
Cb
(
M n = f y S c 2.43 - 1.72
1. Plastificación o fluencia
Lb d
t2
0.08 E
fy
M n = M p = f yZ
1.6 M y
(F11
2. Pandeo lateral por flexo-torsión
0.08 E Lb d
< 2
fy
t
1.9 E
fy
(F11Lb d 1.9 E
<
fy
t2
Propondremos un IR 254 x 38.5 kg/m (10 x 26) con las siguientes propiedades:
DE DISEÑO DE VIGAS
arios ejemplos típicos de miembros en flexión (vigas), resueltos con las Especificaciones
ryy = 3.5 cm
e cualquier otro miembro estructural de acero, consiste en determinar su resistencia disponible
nes que actúan en ella. El diseño es básicamente un problema de revisión, se selecciona un
tiene determinadas propiedades geométricas y mecánicas y se determina su resistencia
, la cual se compara con las solicitaciones que producen las acciones nominales o de diseño.
encia disponible es igual o un poco mayor que las solicitaciones, el diseño es adecuado, si es
ucho mayor, el diseño es antieconómico.
rse requisitos de funcionalidad, incluidos en los estados límite de servicio que estipulan las
ejemplo, los desplazamientos laterales ocasionados por sismo, deflexiones o flechas máximas
exteriores, las cuales no deben exceder de ciertos valores límite que fijan las normas de diseño.
e una viga de acero puede corresponder a alguno de los siguientes fenómenos, los cuales
ente o combinados:
no de cargas, con eventual formación de mecanismo de falla con articulaciones plásticas.
rvalo elástico o aún plástico, caracterizada por pandeo lateral o pandeo lateral por flexo-torsión.
del alma.
J = 16.6 cm4
h0 = d- tf
=
25.08 cm
bf = 6.6
2tf
IR 254 x
d = 39.7
tw
Fig. 18a Sección
La viga se encuentra soportada lateralmente solo al centro del claro por
Lb = 400 cm
Mn = Fy Zx
E
portan grúas viajeras).
Lp = 1.76ryy
fy
b) Si Lp < Lb L
r
[
Mn = Cb M
de las tablas de dimensiones y propiedades de GERDAU CORSA y de acuerdo a las
perfil tipo IR ASTM A992 para una viga que se encuentra simplemente apoyada en sus
figura, capaz de resistir una carga muerta de 350kg/m y una carga viva de 500kg/m, la viga
del claro y la carga de servicio para la revisión de la deflexión considerar: 550 kg/m.
ra ninguna de las revisiones.
Ma = (850) + (8.00)2 =6800kg-m
Z xx
8
Ma Ω b
f y
Z xx
mc70.323
(6800)(1.67)
3515
3
xx
c) Si Lr < Lb
Mn = Fcr sx
Revisión de la longitud no arriostrada:
Z
ua >>
ARRIOSTRAMIENTO AL CENTRO DEL CLARO
8.0 mts.
Lp < Lb < Lr
Fcr =
(
Lb
rT
fy
La sección es compacta en alma
Entonces el momento nominal será:
Fig. 18b Coeficiente de flexión
fy
ndo:
vieron sustituyendo los valores de x en la ecuación general del momento M(x).
ormente calculados en la ecuación del factor de modificación por pandeo lateral – torsional.
exiónb C
= 1.3
en el perfil (relaciones ancho/grueso).
ton-m
fy
kg-cm
ton-m
fy
kg-cm
fy
ton-m
Revisión por cortante
La resistencia nominal por cortante
está dada por:
¡La sección es adecu
Revisión del estado límite de servicio
La deflexión permisible está dada por:
fy
cm
g
33 35
La deflexión elástica de la viga será
o
ton
kg
ton
2.40 cm
b) Si Lp < Lb L
Kg/m
c) Si Lr < Lb
r
(
[
Mn = Cb Mp - (Mp - 0.7FySxx)
b
p
Lr - L p
([
Mp
Mn = Fcr sxx Mp
Cb π2 E
( (
Lb
2
1+0.078
( (
Lb
Jc
Sxxh0 rT
= rcF
rt
g/m
Revisión de la longitud no arriostrada:
cm3
ódulo de sección plástico entraremos a las tablas de dimensiones y propiedades de
para proponer un perfil tipo IR.
R 254 x 38.5 kg/m (10 x 26) con las siguientes propiedades:
Ag = 49.1 cm2
Zxx = 513 cm3
Iyy = 587 cm4
ryy = 3.5 cm
Sxx = 457 cm3
J = 16.6 cm4
h0 = d- tf
IR 254 x 38.5 kg/m
18a Sección transversal ejemplo 1
=
25.08 cm
Cálculo del coeficiente de flexión
rt = 3.9 cm
bf = 6.6
2tf
d = 39.7
tw
soportada lateralmente solo al centro del claro por lo que:
Fig. 18b Coeficiente de flexión
3,515
1´803,195 kg-cm
ton-m
1´124,448 kg-cm
ton-m
uvieron sustituyendo los valores de x en la ecuación general del momento M(x).
ton
eriormente calculados en la ecuación del factor de modificación por
ton-m
¡La sección es adecuada!
Revisión por cortante:
La resistencia nominal por cortante está dada por:
e flexiónCb = 1.3
a en el perfil (relaciones ancho/grueso).
kg
Vn = 33.35 ton
ton
nes.
kg
ton
cm
erá:
kg
ton
cm
Predimensionamiento de la sección:
e la deflexión permisible, en este caso particular se recomienda revisar con un perfil que tenga
n la dirección de la flexión, por ejemplo un IR 305 x 44.5 kg/m el cual tiene una inercia de
cm3
Con este módulo de sección plástico entraremos a las tablas de dimensiones y propie
un perfil IR que cumpla con el requerimiento.
Se eligió un perfil IR 254 x 17.9 kg/m con las siguientes propiedades mecánicas.
decuada!
ente por resistencia, ya que las relaciones ancho espesor del patín y del alma, están dentro del
Sección Plástico es mayor que para el perfil inicialmente propuesto.
na viga simplemente apoyada con carga uniformemente repartida, revisar con las
eleccionar un perfil IR ASTM A992 capaz de soportar el estado límite de falla. La viga se
e en toda su longitud.
VIGA EMBEBIDA EN LA LOSA
IR 254 x 17.9 kg/m
6.0 mts.
Fig. 19a. Sección transversal ejemplo 2
Fig. 19 Viga del ejemplo 2
s en flexión:
Cálculo del momento flexionante actuante de la viga:
La longitud entre soportes laterales de la viga no se revisa ya que se encuentra sopo
por lo que no se revisará este estado límite.
Revisión de las relaciones ancho/espesor:
En el patín:
s en flexión:
kg-m
cm
ma
d = 51.9
tw
La deflexión elástica de la viga será:
es menor que
λpw, por lo que se considera que el alma de la sección es
condición:
Revisión por cortante:
á:
La resistencia nominal por cortante está dada por:
No se acepta la sección, dado que la deflexión elástica es mayor que la permisible y r
Proponemos un IR 305 x 28.2. kg/m con una Inercia de
Ixx = 5,411 cm4.
kg-cm
kg
cm
¡la sección es adecuada en el estado límite de servicio!
cuación:
Para LRFD:
¡La sección es adecuada!
Cargas actuantes:
kg/m
Cálculo del momento flexionante actuante de la viga:
En el patín:
kg
sección:
cm3
bf
lástico entraremos a las tablas de dimensiones y propiedades de GERDAU CORSA para elegir
querimiento.
La relación ancho/espesor del patín en compresión = 9.4
2tf
es no compacta en patín.
λpf,que
es mayor
pero me
En el alma:
kg/m con las siguientes propiedades mecánicas.
IR 254 x 17.9 kg/m
cción transversal ejemplo 2
bf = 101 mm
tf = 5.3 mm
d = 251 mm
tw = 4.8 mm
Zx = 206 cm3
Sxx = 179 cm3
bf
= 9.4
2tf
d = 51.9
tw
d
La relación ancho/espesor del alma = 51.9
tw
compacta.
Dado que se cumple la siguiente condición:
es menor que
λpw, por lo que se conside
La deflexión permisible está dada por:
cm
kg-cm
La deflexión elástica de la viga será:
cuación:
kg-cm
kg-m
cm
No se acepta la sección dado que la deflexión elástica es mayor que la permisible y
revisaremos este estado límite con otro perfil.
Ixx = 5,411 cm4.
Proponemos un IR 305 x 28.2. kg/m con una Inercia de
ecuada!
nte está dada por:
kg
on
cm
¡la sección es adecuada en el estado límite de servicio!
kg
15
7
50
Instalaciones
Plafond
Peso de muros
124
0.0158
7850
m
2
kg/m
2
kg/m
Lámina antiderrapante 5/8”
Fig. 20 Configuración estructural
3
kg/m
Análisis de carga:
Elemento
Consideraciones de carga:
Peso
volumétrico Espesor
C. Muerta
C. Viva
máxima
C.
m
perpendicular de las vigas secundarias @ 1220 mm. El entrepiso tiene como destino una
tura las condiciones de carga se muestran a continuación.
structura
kg/m
kg/m
kg/m
kg/cm
kg/m
kg/m
kg
kg/m
kg/m
4. Estado límite de falla
4.1. Para ASD
s mecánicos de las vigas
cm3
kg/m
4.2. Para LRFD
kg/cm
kg
cm3
kg/m (W 10 x 19) con las siguientes propiedades mecánicas.
stico acudimos a las tablas de dimensiones y propiedades de GERDAU CORSA para elegir
tado límite.
kg/m (W 10 x 19) con las siguientes propiedades mecánicas.
¡La sección es compacta en patín!
La sección es compacta en patines y alma por lo que el momento nominal será igual
IR 254 x 28.5 kg/m
Fig. 20a Sección transversal ejemplo 3
Revisión del pandeo lateral – torsional de la sección
El pandeo lateral – torsional se presenta debido a cargas gravitacionales sobretodo e
puede no estén debidamente arriostradas lateralmente en el patín en compresión.
En este caso particular se colocarán arriostramientos de ángulo @ 1.22 m.
cm3
mm
cm4
mm
cm
cm
Cb .
revisará a continuación haciendo el cálculo del coeficiente de flexión
e flexión tomaremos la parte central de la viga ya que ahí se concentra el mayor esfuerzo de
ntos en los cuartos de la sección no arriostrada
Fig. 20c Coeficiente de flexión (sección cen
Para
m
Para
m
Para
m
Para
m
kg-m
kg-m
´
´
g. 20b Diagrama de momento flexionante
kg-m
kg
ton
4.4.3.1 Para ASD
El cortante actuante es menor que el cortante permisible por lo que la sección es ade
4.4.3.2 Para LRFD
ton
El cortante último es menor que el cortante resistente por lo que la sección es adecua
5. Estado límite de servicio
Para el estado límite de servicio utilizaremos la carga de servicio y revisaremo
gravitacionales comparándola con la que nos permite el AISC.
La deflexión permisible según AISC para vigas sometidas a cargas gravitacionales su
Y la flecha elástica para una viga simplemente apoyada en sus extremos de acuerdo
ó bien utilizando métodos de áreas o doble integración tenemos que:
Para nuestro caso particular la carga de servicio es de:
kg/m
rmisible
stica
cm
viga es menor que la que nos permite el AISC por lo que la sección es adecuada tanto en el
estado límite de servicio.
7. REFERENCIAS
Manual of Steel Construction 2010, American Institute of Steel Construction (AI
Miembros en flexión, Herrera Ricardo, Instituto Latinoamericano del Hierro y el Acero
De Buen O., Estructuras de acero. Comportamiento y diseño, Limusa, México, D.F. 1