1. No category

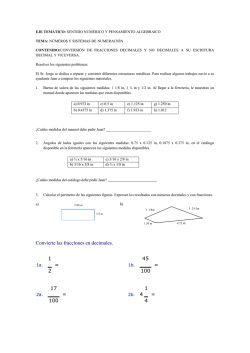
Apreciable alumno:
Se acercan el periodo de exámenes semestrales, en estos se decide la
evaluación del tercer periodo y quién se va a quedar por deber matemáticas.
Considerando ésta situación te propongo el siguiente trabajo con carácter de
obligatorio, que tiene por objetivo que te sirva como guía para presentar tu
examen semestral con mayores probabilidades de éxito.
Incluye los ejercicios de los temas muy parecidos o idénticos, vistos en
clase.
Te sugiero que los resuelvas tu solo con apoyo de tus apuntes, no copies,
porque se perdería el objetivo final que es el que repases.
Entrega tu trabajo con hojas cuadriculadas tamaño carta anexada con los
procedimientos en los que no haya espacio. Basta engrapar las hojas y
entregar en un folder tamaño carta,(No gastes en engargolados ).
Desarrolla a lápiz a y con las respuestas encerradas a tinta de color.
La fecha para entregar este trabajo con valor máximo de un punto es el 17 de
Febrero del 2016.
No se aceptan trabajo después de esta fecha.
“Adelante, siempre adelante”, pues lo quiere San José.
Profesor de la matera:
Emilio Cruz Martínez
COLEGIO “CRISTIANA FERNÁNDEZ DE MERINO”
Trípoli No. 112, Col. Portales, México, D. F. 03300 Tel. 5604-3628, 5605-1509
SECCIÓN SECUNDARIA
GUIA DE EXAMEN SEMESTRAL 2015-2016
MATEMÁTICAS
PRIMER GRADO
NOMBRE DEL ALUMNO(A)
______________________________________________GRADO___FECHA_____
PRIMERA PARTE
1. Calculen el perímetro de las siguientes figuras. Expresen los resultados con números decimales y con
fracciones.
OPERACIONES:
RESPUESTA:
3.5 m
m3.5
________
2. Utilizar los puntos dados en la siguiente recta numérica para ubicar la fracción 2
1
1
1
.
2
1
2
3. Representar en la siguiente recta numérica las fracciones
9
3
y ,
4
2
4. Utilizar los puntos dados en la siguiente recta numérica para ubicar los números decimales 0.8 y 1.20
1
1.5
6.-Transforma las expresiones mixtas a fracciones impropias y resuelve las siguientes operaciones.
3
1
3
-
2
1
6
=
3
2
5
-
2
1
4
=
8. Resuelve los siguientes problemas
A) Elisa compra
OPERACIONES
3
1
kg de papas,
kg de carne y
4
2
2
de tortillas, ¿Cuánto pesa todo junto?
5
RESPUESTA
SEGUNDA PARTE
1. ¿ En qué puntos de la recta están colocados el rombo y el triángulo ?
a)
1
y
8
1
2
1
1
y
4
b)
3
4
1
c)
1
y
5
3
5
1
d)
1
y
4
5
7
1
2. De acuerdo con la siguiente recta numérica, ¿ qué separación hay entre las barras ?
0
2
1
a) 0.875
b) 0.925
c) 0.650
d) 0.750
3. ¿ Qué número decimal representa la distancia qua hay entre la figura y la barra ?
1
0
a) 0.50
b) 0.75
c) 0.25 d) 0.60
2
4. El salón de clase mide 43.56 m . ¿Cuánto medirá por lado este salón si su forma es un cuadrado?
A) 6.6 m
B) 6.7 m
C) 66.6 m
D) 66.7 m
5.- ¿Cuál es el máximo común divisor (m. c. d) de 60, 84, 120?
A) 4 200
B) 420
C) 12
6.
¿Qué número mixto equivale a 13
A) 2.6
B) 1
4
5
D) 6
?
5
C)
26
10
D) 2
3
5
7. Observa la siguiente recta:
¿En cuál de los puntos, señalados por flechas en la recta numérica, se ubica el
número 2.75?
A) a
B) a
C) c
D) d
8. Identifica la figura que tiene exactamente cuatro ejes de simetría.
9. ¿Cuál es la expresión que permite continuar la siguiente sucesión numérica ?
3, 5, 7, 9, ...
a) 2n + 1
b) 2( n + 1 )
c) 2n
d) 2n – 1
10. Observa con atención los recuadros. ¿ Cuántos puntos deberá tener el recuadro siguiente?
a) 2 puntos
b) 8 puntos c) 6 puntos
d) 4 puntos
11. ¿ Cuál es la expresión (fórmula) que satisface la siguiente sucesión numérica ?
0.5, 1.0, 1.5, 2.0, 2.5, …
1
n
n
a) n – 1
b) n – 2
c)
d)
2
2
12. . ¿ Qué valor continúa en la siguiente sucesión ?
1, 4, 9, 16, 25, ...
a) 30
b) 34
c) 36
d) 45
13. Si se utiliza la fórmula x = 4n más 3, ¿ cuál será el quinto valor en la sucesión ?
a) 19
b) 23
c) 21
d) 27
14. Observa con atención la sucesión geométrica ¿ Cuál es la expresión que permite continuar la
correctamente ?
a) x = 2n
b) x = n2 + 1
c) x = 2n2
d) x = 2(n2 – 1 )
15. El período sideral del planeta Marte (tiempo que tarda en dar una vuelta completa
alrededor del Sol) es de aproximadamente 687 días. Este tiempo equivale a ¿cuántos años
terrestres?
a) 1.882 años
b) 0.1882 años
c) 18.82 años
16. Expresión algebraica que se utiliza para formar la sucesión:
12, 15, 18, …
a) 9n + 3
b) 3n + 9
c) 12n + 3
d) 7n + 5
d) 188.2 años
17. Observa la recta que se presenta a continuación, ¿en qué flecha se localiza 1.75?
a) Flecha P
b) Flecha Q
c) Flecha R
d) Flecha S
18. ¿Expresión algebraica que se utiliza para formar la sucesión:
7, 11, 15, 19, …
a) 7n
b) 2n + 1
c) n + 4
d) 4n + 3
19. María va al parque a pasear a su perro y camina cierta distancia, representada en la siguiente recta
numérica:
¿ Cuánto recorrió María con su perro ?
1.
3
2
a)
b)
1
2
c)
7
2
d)
3
2
20.Calculen el perímetro de las siguientes figuras. Expresen los resultados con números decimales y con fracciones.
OPERACIONES:
RESPUESTA:
3.5 m
m3.5
________
21. Utilizar los puntos dados en la siguiente recta numérica para ubicar la fracción 2
22. Representar en la siguiente recta numérica las fracciones
1
.
2
9
3
y ,
4
2
23. Utilizar los puntos dados en la siguiente recta numérica para ubicar los números decimales 0.8 y 1.20
1
1.5
24.Transforma las expresiones mixtas a fracciones impropias y resuelve las siguientes operaciones.
3
1
3
-
2
1
6
=
3
2
5
-
2
1
4
=
25. Resuelve los siguientes problemas
B) Elisa compra
3
1
kg de papas,
kg de carne y
4
2
OPERACIONES
2
de tortillas, ¿Cuánto pesa todo junto?
5
RESPUESTA
TERCERA PARTE:
1. María fue a una fiesta y le regalaron un
de un pastel. Cuando llegó a su casa dividió ese pedazo en
tercios para convidar a su madre y a su hermana. ¿En cuál de las siguientes opciones se expresa lo que le
tocó a cada una del total del pastel?
A)
1
18
B)
1
16
C)
1
12
D)
1
9
2. De los 36 alumnos del grupo “C” sólo asistieron 24, ¿qué fracción del grupo estuvo ausente?
A)
1
6
B)
1
3
C)
2
3
D)
5
6
3. Pedro hace de su casa a la escuela 0.75 más 0.50 de hora, ¿cuánto tiempo hace en realidad?
A) 7.5 minutos.
B) 7.15 minutos.
C) 71.5 minutos.
D) 75 minutos.
4. Don Federico abonó la mitad de su terreno. El primer día que quiso sembrar en dicho
terreno sólo pudo hacerlo en la tercera parte de la tierra abonada. ¿Cuál es la parte del
total del terreno que quedó sembrada ese día?
A)
1
6
B)
2
5
C)
2
3
D)
5. De la capacidad total de un estadio de futbol hay
5
6
5
1
partes que le van al equipo azul y
9
3
que le van al equipo rojo. ¿Qué fracción representa la parte que falta para que se llene el
estadio?
3
6
A) 1
B)
C)
D) 10
9
12
9
18
6.. Rosario compró 3.5 kg de manzanas a $24.90 el kilo. ¿Cuánto pagó por las manzanas?
A) 86.15
B) 87.15
C) 199.2
D) 871.5
8. Los niños Héctor, José, Edgar y Andrés quieren comprar juntos un libro de dinosaurios
que vale $ 76.75. Si Héctor tiene $ 15.30, José $16.75, Edgar $ 17.90 y Andrés
$18.85, ¿cuánto dinero les hace falta para completar el precio del libro?
A) $ 7.95
B) $ 8.05
C) $ 8.95
D) $12.15
8. Fernando compró 2 televisiones y 1 radiograbadora. Si las televisiones le costaron $ 2
760.50 y el total de la compra fue de $ 3 380.80.
¿Cuánto pagó por la radiograbadora?
A) $ 620.30
B) $ 1 620.30
C) $ 2 760.50
D) $ 6 141.30
9. El tiburón blanco tiene 1 de la longitud del tiburón ballena. Si el tiburón ballena mide 35
2
3
m de largo, ¿qué longitud tiene el tiburón blanco?
A)
105 m
6
C) 105 m
2
B) 35 m
6
D)
107 m
6
9. En una tienda de abarrotes venden 5 kg de frijol en $68.50. ¿Cuánto pagarán por 3.5
kg?
A) $ 8.05
B) $ 13.70
C) $ 19.57
D) $ 47.95
RESUELVE:
2
–
3
7 4
1
=
5
2 4
2
 

5 3 15
Problemas:
1. El maestro de electricidad tenía
quedado
2
7 4
 
9 5
1
m de cable eléctrico. Lo usó para mostrar cómo se hace una conexión y le ha
2
3
m, ¿cuánto cable utilizó en la conexión?
4
Operaciones:
Respuesta:
______
4
2. Con un bote de aceite completamente lleno, cuya capacidad es de
litro. ¿Cuántas botellas podrán llenarse?
Operaciones:
3
1
litros, se llenarán botellas de
de
2
4
Respuesta:
______
3)
Un hombre gastó su sueldo de la siguiente manera:
alimentos y
1
1
en el pago de su renta,
en el pago de
5
4
1
en pagos de diversos servicios. ¿Qué fracción del total de su sueldo le quedó después
8
de realizar estos pagos?
Operaciones:
Respuesta:
______
4) Después de aplicar un examen, el maestro les informa a sus alumnos que
1
1
del grupo reprobó,
4
6
aprobó con calificación regular y el resto aprobó con calificación excelente. ¿Qué fracción del grupo
aprobó con calificación excelente?
Operaciones:
Respuesta:
______
5)- Se quieren cortar dos listones de 2,5 m. y 3 m. en trozos de igual longitud y sin que se desperdicie
ningún trozo. ¿Cuál es la longitud del mayor trozo que se puede hacer? ¿Cuántos trozos se obtendrían?
Respuestas
Procedimiento
________
.6)- Los cristales del instituto se limpian cada 9 semanas, los techos cada 12 y las estanterías de la
biblioteca cada 6.
¿Cada cuántas semanas coincidirán las tres tareas?
Respuesta:
Procedimiento
________
CUARTA PARTE
1. María fue a una fiesta y le regalaron un
de un pastel. Cuando llegó a su casa dividió ese pedazo en
tercios para convidar a su madre y a su hermana. ¿En cuál de las siguientes opciones se expresa lo que le
tocó a cada una del total del pastel?
A)
1
18
B)
1
16
C)
1
12
D)
1
9
4. De los 36 alumnos del grupo “C” sólo asistieron 32, ¿qué fracción del grupo estuvo ausente?
A)
1
6
B)
1
3
C)
8
9
D)
5
6
5. Pedro hace de su casa a la escuela 0.75 más 0.75 de hora, ¿cuánto tiempo hace en realidad?
A) 7.5 minutos.
B) 7.15 minutos.
C) 90.0 minutos.
D) 75 minutos.
4. Don Federico abonó la mitad de su terreno. El primer día que quiso sembrar en dicho terreno sólo pudo
hacerlo en la cuarta parte de la tierra abonada. ¿Cuál es la parte del total del terreno que quedó
sembrada ese día?
A)
1
6
2
5
B)
1
8
C)
D)
5. De la capacidad total de un estadio de futbol hay
5
6
5
1
partes que le van al equipo azul y
que le van al
9
18
equipo rojo. ¿Qué fracción representa la parte que falta para que se llene el estadio?
7
3
A) 1
B)
C)
D) 10
9
9
18
18
6.. Rosario compró 5.5 kg de manzanas a $24.90 el kilo. ¿Cuánto pagó por las manzanas?
A) 86.15
B) 87.15
C) 139.95
D) 871.5
6. Los niños Héctor, José, Edgar y Andrés quieren comprar juntos un libro de dinosaurios que vale $
116.75. Si Héctor tiene $ 35.30, José $26.75, Edgar $ 27.90 y Andrés $18.85, ¿cuánto dinero les
hace falta para completar el precio del libro?
A) $ 7.95
B) $ 8.05
C) $ 8.95
D) $12.15
7. Fernando compró 2 televisiones y 1 radiograbadora. Si las dos televisiones le costaron $ 3 760.50 y
el total de la compra fue de $ 4 380.80.
¿Cuánto pagó por la radiograbadora?
A) $ 620.30
B) $ 1 620.30
C) $ 3 620.30
D) $ 6 141.30
45
1
de la longitud del tiburón ballena. Si el tiburón ballena mide
m de largo,
2
4
¿qué longitud tiene el tiburón blanco?
9. El tiburón blanco tiene
A)
105 m
6
B) 35 m
6
C)
105
m
8
D)
45
m
8
10. En una tienda de abarrotes venden 6 kg de frijol en $82.20. ¿Cuánto pagarán por 4.5 kg?
A) $ 8.05
B) $ 13.70
C) $ 61.65
D) $ 47.95
PROBLEMAS:
1. El maestro de electricidad tenía
conexión y le ha quedado
Operaciones:
3
1
m de cable eléctrico. Lo usó para mostrar cómo se hace una
2
5
m, ¿cuánto cable utilizó en la conexión?
4
Respuesta:
______
2. Con un bote de aceite completamente lleno, cuya capacidad es de
1
botellas de
de litro. ¿Cuántas botellas podrán llenarse?
4
Operaciones:
5
1
litros, se llenarán
2
Respuesta:
______
3)
Un hombre gastó su sueldo de la siguiente manera:
alimentos y
1
1
en el pago de su renta,
en el pago de
4
8
3
en pagos de diversos servicios. ¿Qué fracción del total de su sueldo le quedó después
5
de realizar estos pagos?
Operaciones:
Respuesta:
______
4)- Se quieren cortar dos listones de 3,8 m. y 4 m. en trozos de igual longitud y sin que se desperdicie
ningún trozo. ¿Cuál es la longitud del mayor trozo que se puede hacer? ¿Cuántos trozos se obtendrían?
Respuestas
Procedimiento
________
.5)- Los cristales del instituto se limpian cada 10 semanas, los techos cada 8 y las estanterías de la
biblioteca cada 2.
¿Cada cuántas semanas coincidirán las tres tareas?
Respuesta:
Procedimiento
________
6. Calcula el àrea de las figura sustituyendo los valores en las fórmulas correspondientes (fíjate bien en
las unidades resultantes).
Área:_______
8 mm
18 mm
8. Los lados de un cuadrilátero miden 5, 9, 2 y 11 cm, Si se realizan reproducciones a escala ¿cuánto
deben medir los demás lados?
Medidas de los
lados de la figura
original
5 cm
2 cm
9 cm
11cm
Medidas de los
lados de la
figura original
9 cm
2 cm
5 cm
11cm
Medidas de los lados
de la reproducción
15 cm
8. Traza un segmento cualquiera y su
mediatriz y con ellos dibuja un rombo
Medidas de los lados
de la reproducción
6 cm
9. Traza con algún color la bisectriz de los
ángulos interiores de cada figura, con otro color
las diagonales y con un color diferente la mediatriz
de cada lado
9. Resuelvan el siguiente problema: La tabla contiene diferentes cantidades de litros de gasolina y sus
respectivos precios.
Litros de
gasolina
1
Total a pagar
3
21
9
42
420
10. Escribe los números en las siguientes tablas de modo que se establezca el factor de
proporcionalidad que se indica:
a) factor de proporcionalidad = 2.6
4
7
QUINQTA PARTE:
I. Resuelve las siguientes operaciones
1)
65 93.972
10
13
2)
2.74 39.485
18
3)
961.15 ÷ 0.5 = ______
4)
577.4 ÷ 7.4 = ______
II. Resuelve las siguientes ecuaciones puedes aplicar las propiedades de la igualdad o transponer
los términos.
5)
x + 10 = 15
6)
37 + x = 84
7)
8)
2x + 3 = 47
9)
18 + 6x = 90
10)
x + 12 = 71
9x + 17 = 134
III.Resuelve los siguientes problemas.
1. Elsa quiere cortar un listón que mide 6.95 cm 2. En un zoológico se compraron 342 kilogramos
en 15 partes iguales ¿cuánto listón le sobrará ?
de alpiste para alimentar a las aves. Si el
Operaciones
Respuesta
cuidador desea repartirlo en sacos de 2.5
kilogramos.
¿ Cuántos sacos tendrá ? y ¿Sobra algo de
alpiste ?
Operaciones
Respuesta
3. En un almacén el precio del pantalón es el
doble de la camisa, si el precio de las dos
prendas es de $ 1 731 ¿Cuánto cuesta cada
prenda ?
Ecuaciòn
Respuesta
4. Un equipo de futbol ha jugado 85 partidos, si el
número de juegos ganados excede en 25 a los
perdidos ¿ Cuántos juegos ha ganado ?
Ecuaciòn
Respuesta
5. Un cordón de 516 cm se divide en dos partes, 6. La suma de las edades de un padre y su hijo
de tal forma que la medida de una de ellas es el es de 49 años, el padre tiene 25 años más que su
triple de la medida de la otra. Encuentra la hijo, ¿ cuál es la edad actual de cada uno ?
Ecuaciòn
Respuesta
medida de cada parte.
Ecuaciòn
Respuesta
IV. Efectuar las siguientes construcciones utilizando regla y compás
1. Un hexágono regular
VI. Realiza los càlculos indicados.
1. Encuentra la suma total de los ángulos
inteiores de un dodecàgono regular.
Fòrmula y operaciones
resultado
2. Un triángulo equilátero
2. Encuentra la medida de un angulo interior
de un decàgono regular.
Fòrmula y operaciones
resultado
De acuerdo con la escala di si es una ampliación o una reducción.
Escala
1
2
7
4
Reducción o ampliación
Escala
6:3
2 : 20
Reducción o
ampliación
En las dos figuras que en cada caso se dan, la segunda es rep roducción a escala de la primera o
sea son semejantes. Determina el factor a que está construida la segunda figura.
1)
2)
56
7
72
9
33
3
3)
d)
2
5
5)
6)
35
15
36
15
Escribe el factor inverso de cada una de las siguientes escalas.
Escala
3
4
Factor inverso a la
escala
Escala
Factor inverso a la
escala
36
5
Escala
Factor inverso a la
escala
1 800
70
Resuelve los siguientes problemas
1. Una fotocopia se redujo a 12 cm de ancho y 9 cm de alto. ¿ cuáles serán sus medidas reales si se
2
disminuyó a una escala de
?
3
2. Si a una litografía se le aplica una escala
cm, ¿ cuáles eran las medidas originales ?
3
y queda con una altura de 78 cm y de ancho 105
1